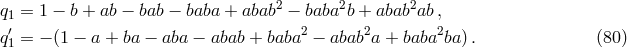5 Time-Delay Interferometry with Moving Spacecraft
The rotational motion of the LISA array results in a difference of the light travel times in the two directions around a Sagnac circuit [44*, 7*]. Two time delays along each arm must be used, say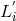 and
and 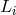 for clockwise or counter-clockwise propagation as they enter in any of the TDI
combinations. Furthermore, since
for clockwise or counter-clockwise propagation as they enter in any of the TDI
combinations. Furthermore, since 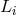 and
and 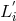 not only differ from one another but can be time
dependent (they “flex”), it was shown that the “first generation” TDI combinations do not
completely cancel the laser phase noise (at least with present laser stability requirements), which can
enter at a level above the secondary noises. For LISA, and assuming
not only differ from one another but can be time
dependent (they “flex”), it was shown that the “first generation” TDI combinations do not
completely cancel the laser phase noise (at least with present laser stability requirements), which can
enter at a level above the secondary noises. For LISA, and assuming 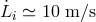 [21*], the
estimated magnitude of the remaining frequency fluctuations from the laser can be about 30 times
larger than the level set by the secondary noise sources in the center of the frequency band. In
order to solve this potential problem, it has been shown that there exist new TDI combinations
that are immune to first order shearing (flexing, or constant rate of change of delay times).
These combinations can be derived by using the time-delay operators formalism introduced in
the previous Section 4, although one has to keep in mind that now these operators no longer
commute [58*].
[21*], the
estimated magnitude of the remaining frequency fluctuations from the laser can be about 30 times
larger than the level set by the secondary noise sources in the center of the frequency band. In
order to solve this potential problem, it has been shown that there exist new TDI combinations
that are immune to first order shearing (flexing, or constant rate of change of delay times).
These combinations can be derived by using the time-delay operators formalism introduced in
the previous Section 4, although one has to keep in mind that now these operators no longer
commute [58*].
In order to derive the new, “flex-free” TDI combinations we will start by taking specific
combinations of the one-way data entering in each of the expressions derived in the previous Section 4.
Note, however, that now the expressions for the  -measurements assume the following form
-measurements assume the following form
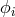 ,
,  measurements are as given in Eq. (38*).
measurements are as given in Eq. (38*).
The new TDI combinations are chosen in such a way so as to retain only one of the three
noises 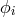 ,
, 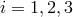 , if possible. In this way we can then implement an iterative procedure
based on the use of these basic combinations and of time-delay operators, to cancel the laser
noises after dropping terms that are quadratic in
, if possible. In this way we can then implement an iterative procedure
based on the use of these basic combinations and of time-delay operators, to cancel the laser
noises after dropping terms that are quadratic in  or linear in the accelerations. This
iterative time-delay method, to first order in the velocity, is illustrated abstractly as follows. Given
a function of time
or linear in the accelerations. This
iterative time-delay method, to first order in the velocity, is illustrated abstractly as follows. Given
a function of time  , time delay by
, time delay by 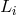 is now denoted either with the standard
comma notation [2*] or by applying the delay operator
is now denoted either with the standard
comma notation [2*] or by applying the delay operator 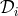 introduced in the previous Section 4,
introduced in the previous Section 4,
 :
A third time delay
:
A third time delay 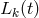 gives
and so on, recursively; each delay generates a first-order correction proportional to its rate of
change times the sum of all delays coming after it in the subscripts. Commas have now been
replaced with semicolons [45*], to remind us that we consider moving arrays. When the sum
of these corrections to the terms of a data combination vanishes, the combination is called
flex-free.
gives
and so on, recursively; each delay generates a first-order correction proportional to its rate of
change times the sum of all delays coming after it in the subscripts. Commas have now been
replaced with semicolons [45*], to remind us that we consider moving arrays. When the sum
of these corrections to the terms of a data combination vanishes, the combination is called
flex-free.
Also, note that each delay operator  has a unique inverse
has a unique inverse 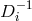 , whose expression can be derived
by requiring that
, whose expression can be derived
by requiring that  , and neglecting quadratic and higher order velocity terms. Its action on a
time series
, and neglecting quadratic and higher order velocity terms. Its action on a
time series  is
is
 but rather
but rather
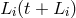 .
.
5.1 The unequal-arm Michelson
The unequal-arm Michelson combination relies on the four measurements 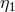 ,
, 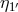 ,
, 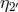 , and
, and 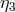 . Note
that the two combinations
. Note
that the two combinations 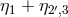 ,
, 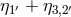 represent the two synthesized two-way data measured
onboard spacecraft 1, and can be written in the following form (see Eqs. (47*), (48*), and (49*) for deriving
the following synthesized two-way measurements)
represent the two synthesized two-way data measured
onboard spacecraft 1, and can be written in the following form (see Eqs. (47*), (48*), and (49*) for deriving
the following synthesized two-way measurements)
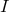 is the identity operator. Since in the stationary case any pairs of these operators commute, i.e.,
is the identity operator. Since in the stationary case any pairs of these operators commute, i.e.,
 , from Eqs. (54*) and (55*) it is easy to derive the following expression for the
unequal-arm interferometric combination
, from Eqs. (54*) and (55*) it is easy to derive the following expression for the
unequal-arm interferometric combination 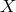 which eliminates
which eliminates  :
If, on the other hand, the time-delays depend on time, the expression of the unequal-arm Michelson
combination above no longer cancels
:
If, on the other hand, the time-delays depend on time, the expression of the unequal-arm Michelson
combination above no longer cancels 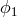 . In order to derive the new expression for the unequal-arm
interferometer that accounts for “flexing”, let us first consider the following two combinations of the
one-way measurements entering into the
. In order to derive the new expression for the unequal-arm
interferometer that accounts for “flexing”, let us first consider the following two combinations of the
one-way measurements entering into the 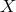 observable given in Eq. (56*):
Using Eqs. (57*) and (58*), we can use the delay technique again to finally derive the following
expression for the new unequal-arm Michelson combination
observable given in Eq. (56*):
Using Eqs. (57*) and (58*), we can use the delay technique again to finally derive the following
expression for the new unequal-arm Michelson combination 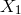 that accounts for the flexing effect:
As usual,
that accounts for the flexing effect:
As usual, 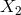 and
and 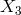 are obtained by cyclic permutation of the spacecraft indices. This expression is
readily shown to be laser-noise-free to first order of spacecraft separation velocities
are obtained by cyclic permutation of the spacecraft indices. This expression is
readily shown to be laser-noise-free to first order of spacecraft separation velocities 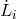 : it is
“flex-free”.
: it is
“flex-free”.
5.2 The Sagnac combinations
In the above Section 5.1, we have used the same symbol  for the unequal-arm Michelson combination
for both the rotating (i.e., constant delay times) and stationary cases. This emphasizes that, for this TDI
combination (and, as we will see below, also for all the combinations including only four links) the forms of
the equations do not change going from systems at rest to the rotating case. One needs only distinguish
between the time-of-flight variations in the clockwise and counter-clockwise senses (primed and unprimed
delays).
for the unequal-arm Michelson combination
for both the rotating (i.e., constant delay times) and stationary cases. This emphasizes that, for this TDI
combination (and, as we will see below, also for all the combinations including only four links) the forms of
the equations do not change going from systems at rest to the rotating case. One needs only distinguish
between the time-of-flight variations in the clockwise and counter-clockwise senses (primed and unprimed
delays).
In the case of the Sagnac variables  , however, this is not the case as it is easy
to understand on simple physical grounds. In the case of
, however, this is not the case as it is easy
to understand on simple physical grounds. In the case of  for instance, light originating
from spacecraft 1 is simultaneously sent around the array on clockwise and counter-clockwise
loops, and the two returning beams are then recombined. If the array is rotating, the two beams
experience a different delay (the Sagnac effect), preventing the noise
for instance, light originating
from spacecraft 1 is simultaneously sent around the array on clockwise and counter-clockwise
loops, and the two returning beams are then recombined. If the array is rotating, the two beams
experience a different delay (the Sagnac effect), preventing the noise  from canceling in the
from canceling in the 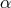 combination.
combination.
In order to find the solution to this problem let us first rewrite 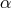 in such a way to explicitly emphasize
what it does: attempts to remove the same fluctuations affecting two beams that have been made to
propagated clockwise and counter-clockwise around the array,
in such a way to explicitly emphasize
what it does: attempts to remove the same fluctuations affecting two beams that have been made to
propagated clockwise and counter-clockwise around the array,
 that is unaffected by laser noise in presence of rotation,
If the delay-times are also time-dependent, we find that the residual laser noise remaining into the
combination
that is unaffected by laser noise in presence of rotation,
If the delay-times are also time-dependent, we find that the residual laser noise remaining into the
combination 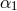 is actually equal to
Fortunately, although first order in the relative velocities, the residual is small, as it involves the difference
of the clockwise and counter-clockwise rates of change of the propagation delays on the same circuit. For
LISA, the remaining laser phase noises in
is actually equal to
Fortunately, although first order in the relative velocities, the residual is small, as it involves the difference
of the clockwise and counter-clockwise rates of change of the propagation delays on the same circuit. For
LISA, the remaining laser phase noises in  ,
, 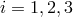 , are several orders of magnitude below the
secondary noises.
, are several orders of magnitude below the
secondary noises.
In the case of 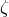 , however, the rotation of the array breaks the symmetry and therefore its uniqueness.
However, there still exist three generalized TDI laser-noise-free data combinations that have
properties very similar to
, however, the rotation of the array breaks the symmetry and therefore its uniqueness.
However, there still exist three generalized TDI laser-noise-free data combinations that have
properties very similar to 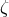 , and which can be used for the same scientific purposes [54]. These
combinations, which we call
, and which can be used for the same scientific purposes [54]. These
combinations, which we call 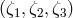 , can be derived by applying again our time-delay operator
approach.
, can be derived by applying again our time-delay operator
approach.
Let us consider the following combination of the  ,
, 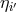 measurements, each being delayed only
once [2*]:
measurements, each being delayed only
once [2*]:
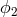 and
and 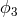 terms. Since both sides of the two equations above contain only the
terms. Since both sides of the two equations above contain only the  noise,
noise, 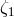 is found by the
following expression:
If the light-times in the arms are equal in the clockwise and counter-clockwise senses (e.g., no rotation)
there is no distinction between primed and unprimed delay times. In this case,
is found by the
following expression:
If the light-times in the arms are equal in the clockwise and counter-clockwise senses (e.g., no rotation)
there is no distinction between primed and unprimed delay times. In this case, 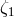 is related to our original
symmetric Sagnac
is related to our original
symmetric Sagnac 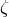 by
by  . Thusm for the LISA case (arm length difference
. Thusm for the LISA case (arm length difference 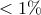 ), the
SNR of
), the
SNR of 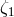 will be the same as the SNR of
will be the same as the SNR of  .
.
If the delay-times also change with time, the perfect cancellation of the laser noises is no longer achieved
in the  combinations. However, it has been shown in [58*] that the magnitude of the residual
laser noises in these combinations are significantly smaller than the LISA secondary system noises, making
their effects entirely negligible.
combinations. However, it has been shown in [58*] that the magnitude of the residual
laser noises in these combinations are significantly smaller than the LISA secondary system noises, making
their effects entirely negligible.
The expressions for the Monitor, Beacon, and Relay combinations, accounting for the rotation and flexing of the LISA array, have been derived in the literature [58*] by applying the time-delay iterative procedure highlighted in this section. The interested reader is referred to that paper for details.
5.3 Algebraic approach to second-generation TDI
In this subsection we present a mathematical formulation of the “second-generation” TDI, which generalizes the one presented in Section 4 for stationary LISA. Although a full solution as in the case of stationary LISA seems difficult to obtain, significant progress can be made.
There is, however, a case in between the 1st and 2nd generation TDI, called modified first-generation
TDI, in which only the Sagnac effect is considered [7, 44]. In this case the up-down links are unequal while
the delay-times remain constant. The mathematical formulation of Section 4 can be extended in a
straight-forward way where now the six time-delays 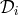 and
and 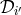 must be taken into account. The
polynomial ring still remains commutative but it is now in six variables. The corresponding module of
syzygies can be constructed over this larger polynomial ring [41].
must be taken into account. The
polynomial ring still remains commutative but it is now in six variables. The corresponding module of
syzygies can be constructed over this larger polynomial ring [41].
When the arms are allowed to flex, that is, the operators themselves are functions of time, the operators
no longer commute. One must then resort to non-commutative algebra. We outline the procedure below.
Since lot of the discussion has been covered in the previous subsections we just describe the
algebraic formulation. The equation Eq. (26*) generalizes in two ways: (1) we need to consider now
six operators 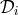 and
and 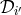 , and (2) we need to take into account the non-commutativity of
the operators – the order of the operators is important. Accordingly Eq. (26*) generalizes to,
, and (2) we need to take into account the non-commutativity of
the operators – the order of the operators is important. Accordingly Eq. (26*) generalizes to,
Eliminating 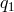 and
and 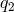 from the three Eqs. (68*) while respecting the order of the variables we get:
from the three Eqs. (68*) while respecting the order of the variables we get:
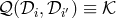 , is non-commutative, of polynomials in the six variables
, is non-commutative, of polynomials in the six variables
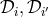 and coefficients in the rational field
and coefficients in the rational field 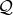 . The polynomial vectors
. The polynomial vectors 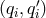 satisfying
the above equations form a left module over
satisfying
the above equations form a left module over 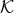 . A left module means that one can multiply
a solution
. A left module means that one can multiply
a solution 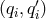 from the left by any polynomial in
from the left by any polynomial in 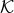 , then it is also a solution to the
Eqs. (68*) and, therefore, in the module – the module of noise-free TDI observables. For details
see [9].
, then it is also a solution to the
Eqs. (68*) and, therefore, in the module – the module of noise-free TDI observables. For details
see [9].
When the operators do not commute, the algebraic problem is far more complex. If we
follow on the lines of the commutative case, the first step would be to find a Gröbner basis for
the ideal generated by the coefficients appearing in Eq. (69*), namely, the set of polynomials
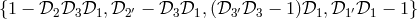 . Although we may be able to apply
non-commutative Gröbner basis methods, the general solution seems quite difficult. However,
simplifications are possible because of the inherent symmetries in the problem and so the ring
. Although we may be able to apply
non-commutative Gröbner basis methods, the general solution seems quite difficult. However,
simplifications are possible because of the inherent symmetries in the problem and so the ring 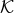 can be
quotiented by a certain ideal, simplifying the algebraic problem. One then needs to deal with a ‘smaller’
ring, which may be easier to deal with. We describe below how this can achieved with the help of certain
commutators.
can be
quotiented by a certain ideal, simplifying the algebraic problem. One then needs to deal with a ‘smaller’
ring, which may be easier to deal with. We describe below how this can achieved with the help of certain
commutators.
In general, a commutator of two operators 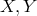 is defined as the operator
is defined as the operator ![[X, Y ] ≡ XY − Y X](article570x.gif) . In
our situation
. In
our situation 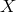 and
and 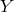 are strings of operators built up of the operators
are strings of operators built up of the operators 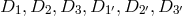 . For
example, in the Sagnac combination the following commutator [12*] occurs:
. For
example, in the Sagnac combination the following commutator [12*] occurs:
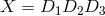 and
and  . This commutator leads to the residual noise term given in
Eq. (64*) and which happens to be small. In the context of the reasonably optimized model of LISA say
given in [12*], the residual noise term is small. For this model, we have
. This commutator leads to the residual noise term given in
Eq. (64*) and which happens to be small. In the context of the reasonably optimized model of LISA say
given in [12*], the residual noise term is small. For this model, we have 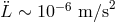 and thus,
even if one considers say 20 successive optical paths, that is, about
and thus,
even if one considers say 20 successive optical paths, that is, about 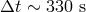 of light travel
time,
of light travel
time, 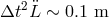 . This is well below few meters and thus can be neglected in the residual
laser noise computation. Moreover,
. This is well below few meters and thus can be neglected in the residual
laser noise computation. Moreover, 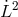 terms (and higher order) can be dropped since they
are of the order of
terms (and higher order) can be dropped since they
are of the order of 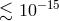 (they come with a factor
(they come with a factor 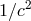 ), which is much smaller than 1
part in
), which is much smaller than 1
part in  , which is the level at which the laser frequency noise must be canceled. Thus, we
keep terms only to the first degree in
, which is the level at which the laser frequency noise must be canceled. Thus, we
keep terms only to the first degree in 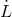 and also neglect higher time derivative terms in
and also neglect higher time derivative terms in
 .
.
The result for the Sagnac combination can be generalized. In order to simplify notation we
write 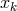 or
or 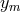 for the time-delay operators, where
for the time-delay operators, where 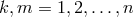 and
and  , that
is,
, that
is, 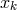 or
or 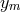 are any of the operators
are any of the operators 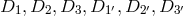 . Then a commutator is:
. Then a commutator is:
 :
:
Note that the LHS acts on 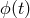 , while the right-hand side multiplies
, while the right-hand side multiplies 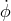 at an appropriately
delayed time. For the Sagnac combination this is readily seen from Eq. (64*). Also the notation on
the RHS is obvious: if for some
at an appropriately
delayed time. For the Sagnac combination this is readily seen from Eq. (64*). Also the notation on
the RHS is obvious: if for some 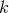 , we have,
, we have, 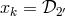 say, then
say, then 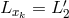 and so on; the
same holds for
and so on; the
same holds for 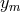 for a given
for a given 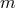 . From this equation it immediately follows that if the
operators
. From this equation it immediately follows that if the
operators 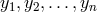 are a permutation of the operators
are a permutation of the operators 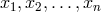 , then the commutator,
, then the commutator,
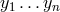 is a
permutation of
is a
permutation of  then both polynomials trace the same links, except that the nodes (spacecraft) of
the links are taken in different orders. If the armlengths were constant, the pathlengths would be identical
and the commutator would be zero. But here, by neglecting
then both polynomials trace the same links, except that the nodes (spacecraft) of
the links are taken in different orders. If the armlengths were constant, the pathlengths would be identical
and the commutator would be zero. But here, by neglecting 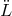 terms and those of higher orders, we have
effectively assumed that
terms and those of higher orders, we have
effectively assumed that 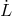 s are constant, so the increments also cancel out, resulting in a vanishing
commutator.
s are constant, so the increments also cancel out, resulting in a vanishing
commutator.
These vanishing commutators (in the approximation we are working in) can be used to simplify the
algebra. We first construct the ideal 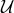 generated by the commutators such as those given by Eq. (73*).
Then we quotient the ring
generated by the commutators such as those given by Eq. (73*).
Then we quotient the ring 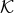 by
by 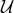 , thereby constructing a smaller ring
, thereby constructing a smaller ring  . This ring is smaller
because it has fewer distinct terms in a polynomial. Although, this reduces the complexity of the problem, a
full solution to the TDI problem is still lacking.
. This ring is smaller
because it has fewer distinct terms in a polynomial. Although, this reduces the complexity of the problem, a
full solution to the TDI problem is still lacking.
In the following Section 5.4, we will consider the case where we have only two arms of LISA in operation, that is one arm is nonfunctional. The algebraic problem simplifies considerably and it turns out to be tractable.
5.4 Solutions with one arm nonfunctional
We must envisage the possibility that not all optical links of LISA can be operating at all times for various reasons like technical failure for instance or even the operating costs. An analysis covering the scientific capabilities achievable by LISA in the eventuality of loosing one and two links has been discussed in [62]. Here we obtain the TDI combinations when one entire arm becomes dysfunctional. See [11*] for a full discussion. The results of this section are directly usable by the eLISA/NGO mission.
We arbitrarily choose the non-functional arm to be the one connecting S/C 2 and S/C 3. This means
from our labeling that the polynomials are now restricted to only the four operators 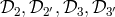 and
we can set the polynomials
and
we can set the polynomials 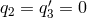 . This simplifies the Eqs. (68*) considerably because the last two
equations reduce to
. This simplifies the Eqs. (68*) considerably because the last two
equations reduce to 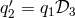 and
and 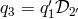 . Substituting these in the first equation gives just one
equation:
. Substituting these in the first equation gives just one
equation:
If we can solve this equation for 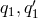 then the full polynomial vector can be obtained because
then the full polynomial vector can be obtained because
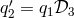 and
and 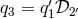 . It is clear that solutions are of the Michelson type. Also notice that the
coefficients of this equation has the operators
. It is clear that solutions are of the Michelson type. Also notice that the
coefficients of this equation has the operators 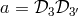 and
and 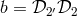 occurring in them. So the
solutions
occurring in them. So the
solutions 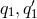 too will be in terms of
too will be in terms of  and
and 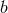 only. Physically, the operators
only. Physically, the operators  and
and 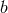 correspond
to round trips.
correspond
to round trips.
One solution has already been given in the literature [1, 61*]. This solution in terms of 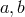 is:
is:
![Δ = [ba,ab]](article632x.gif) , which is a commutator that vanishes since
, which is a commutator that vanishes since 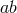 is a permutation of
is a permutation of
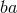 . Thus, it is an element of
. Thus, it is an element of 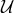 and Eq. (75*) is a solution (over the quotient ring).
and Eq. (75*) is a solution (over the quotient ring).
What we would like to emphasize is that there are more solutions of this type – in fact there are infinite number of such solutions. The solutions are based on vanishing of commutators. In [11*] such commutators are enumerated and for each such commutator there is a corresponding solution. Further an algorithm is given to construct such solutions.
We briefly mention some results given in [11*]. We start with the solutions 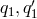 of Eq. (75*). Note
that these are of degree 3 in
of Eq. (75*). Note
that these are of degree 3 in  and
and 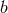 . The commutator corresponding to this solution is
. The commutator corresponding to this solution is
![2 2 Δ = [ba,ab] = ba b − ab a](article639x.gif) and is of degree 4. There is only one such commutator at degree 4 and
therefore one solution. The next higher degree solutions are found when the commutators have degree 8.
The solutions
and is of degree 4. There is only one such commutator at degree 4 and
therefore one solution. The next higher degree solutions are found when the commutators have degree 8.
The solutions  are of degree 7. There are three such commutators at degree 8. We list the solutions
and the commutators below. One solution is:
are of degree 7. There are three such commutators at degree 8. We list the solutions
and the commutators below. One solution is:
The second solution is:
whose commutator is![Δ = [b2a2,a2b2]](article644x.gif) .
.
The third solution corresponds to the commutator ![[baba,abab]](article645x.gif) . This solution is given by:
. This solution is given by:
Higher degree solutions can be constructed. An iterative algorithm has been described in [11] for this
purpose. The degrees of the commutators are in multiples of 4. If we call the degree of the commutators as
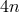 where
where 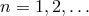 , then the solutions
, then the solutions  are of degree
are of degree 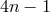 . The cases mentioned above,
correspond to
. The cases mentioned above,
correspond to 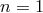 and
and 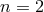 . The general formula for the number of commutators of degree
. The general formula for the number of commutators of degree 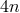 is
is
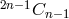 . So at
. So at 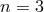 we have 10 commutators and so as many solutions
we have 10 commutators and so as many solutions 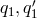 of degree
11.
of degree
11.
These are the degrees of polynomials of 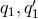 in the operators
in the operators 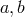 . But for the full polynomial
vector, which has
. But for the full polynomial
vector, which has  and
and 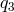 , we need to go over to the operators expressed in terms of
, we need to go over to the operators expressed in terms of 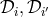 . Then
the degree of each of the
. Then
the degree of each of the 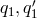 is doubled to
is doubled to 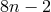 , while
, while 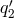 and
and 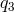 are each of degree
are each of degree 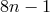 .
Thus, for a general value of
.
Thus, for a general value of 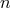 , the solution contains polynomials of maximum degree
, the solution contains polynomials of maximum degree 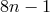 in the
time-delay operators.
in the
time-delay operators.
From the mathematical point of view there is an infinite family of solutions. Note that no claim is made on exhaustive listing of solutions. However the family of solutions is sufficiently rich, because we can form linear combinations of these solutions and they also are solutions.
From the physical point of view, since terms in 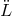 and
and  and higher orders have been neglected, a
limit on the degree of the polynomial solutions arises. That is up to certain degree of the polynomials, we
can safely assume the commutators to vanish. But as the degree of the polynomials increases it
is not possible to neglect these higher order terms any longer and then such a limit becomes
important. The limit is essentially set by
and higher orders have been neglected, a
limit on the degree of the polynomial solutions arises. That is up to certain degree of the polynomials, we
can safely assume the commutators to vanish. But as the degree of the polynomials increases it
is not possible to neglect these higher order terms any longer and then such a limit becomes
important. The limit is essentially set by 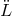 . We now investigate this limit and make a very
rough estimate of it. As mentioned earlier, the LISA model in [12] gives
. We now investigate this limit and make a very
rough estimate of it. As mentioned earlier, the LISA model in [12] gives 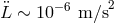 .
From
.
From 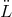 we compute the error in
we compute the error in 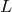 , namely,
, namely, 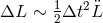 . If we allow the error to be no
more than say 10 meters, then we find
. If we allow the error to be no
more than say 10 meters, then we find 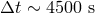 . Since each time-delay is about 16.7 s for
LISA, the number of successive time-delays is about 270. This is the maximum degree of the
polynomials. This means one can go up to
. Since each time-delay is about 16.7 s for
LISA, the number of successive time-delays is about 270. This is the maximum degree of the
polynomials. This means one can go up to 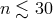 . If we set the limit more stringently at
. If we set the limit more stringently at
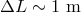 , then the highest degree of the polynomial reduces to about 80, which means one
can go up to
, then the highest degree of the polynomial reduces to about 80, which means one
can go up to 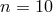 . Thus, there are a large number of TDI observables available to do the
physics.
. Thus, there are a large number of TDI observables available to do the
physics.
Some remarks are in order:
- A geometric combinatorial approach was adopted in [61] where several solutions were presented. Our approach is algebraic where the operations are algebraic operations on strings of operators. The algebraic approach has the advantage of easy manipulation of data streams, although some geometrical insight could be at a premium.
- Another important aspect is the GW response of such TDI observables. The GW response to a TDI observable may be calculated in the simplest way by assuming equal arms (the possible differences in lengths would be sensitive to frequencies outside the LISA bandwidth). This leads in the Fourier domain to polynomials in the same phase factor from which the signal to noise ratio can be found. A comprehensive and generic treatment of the responses of second-generation TDI observables can be found in [30].

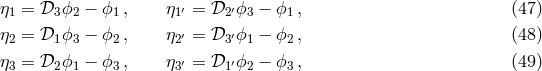

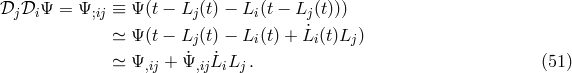
![𝒟 𝒟 𝒟 Ψ = Ψ = Ψ (t − L (t) − L (t − L (t)) − L (t − L (t) − L (t − L (t)))) k j i ;ijk k [ j k i ] k j k ≃ Ψ,ijk + ˙Ψ,ijk L˙i (Lj + Lk) + ˙LjLk , (52 )](article492x.gif)


 − [(𝒟3𝒟3 ′ − I )](η1′ + η3,2′) . (56 )](article511x.gif)
![[(η1′ + η3;2′) + (η1 + η2′;3);22′] = [D2 ′D2D3D3 ′ − I]ϕ1 , (57 ) [(η1 + η2′;3) + (η1′ + η3;2′);3′3] = [D3D3 ′D2 ′D2 − I]ϕ1 . (58 )](article514x.gif)
![X1 = [D2 ′D2D3D3 ′ − I][(η1 + η2′;3′) + (η1′ + η3;2′);3′3] − [D D ′D ′D − I][(η′ + η ′) + (η + η ′ ) ′]. (59 ) 3 3 2 2 1 3;2 1 2;3 ;22](article516x.gif)
![α = [η ′ + 𝒟 ′η ′ + 𝒟 ′𝒟 ′η′] − [η + 𝒟 η + 𝒟 𝒟 η ], (60 ) 1 2 3 1 2 2 1 3 2 1 3 2](article526x.gif)
![[η1′ + 𝒟2 ′η3′ + 𝒟1′𝒟2 ′η2′] = [𝒟2 ′𝒟1 ′𝒟3 ′ − I ]ϕ1 (61 ) [η + 𝒟 η + 𝒟 𝒟 η ] = [𝒟 𝒟 𝒟 − I]ϕ . (62 ) 1 3 2 1 3 2 3 1 2 1](article527x.gif)
![α1 = [𝒟3𝒟1 𝒟2 − I][η1′ + 𝒟2′η3′ + 𝒟1 ′𝒟2 ′η2′] − [𝒟2 ′𝒟1 ′𝒟3 ′ − I][η1 + 𝒟3 η2 + 𝒟1 𝒟3 η2]. (63 )](article529x.gif)
![˙ [( ˙ ˙ ˙ ) ( ′ ′ ′) ( ˙′ ˙′ ˙′) ] ϕ1,1231′2′3′ L1 + L2 + L3 L 1 + L 2 + L3 − L1 + L2 + L3 (L1 + L2 + L3 ) . (64 )](article531x.gif)
![η3,3 − η3′,3 + η1,1′ = [D3D2 − D1 ′]ϕ1 , (65 ) η1′,1 − η2,2′ + η2′,2′ = [D3′D2 ′ − D1 ]ϕ1 , (66 )](article539x.gif)
 − [D2D3 − D1 ′](η1′,1 − η2,2′ + η2′,2′). (67 )](article544x.gif)

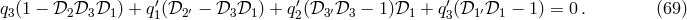
![[D D D ,D ′D ′D ′] ≡ D D D D ′D ′D ′ − D ′D ′D ′D D D . (70 ) 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3](article574x.gif)
![[x1x2...xn, y1y2...yn] = x1x2 ...xny1y2...yn − y1y2 ...ynx1x2 ...xn. (71 )](article593x.gif)
![[x1x2 ...xn,y1y2...yn ] ϕ(t) ( ∑n ∑n ∑n ∑n ) ( ∑n ∑n ) = Lx ˙Lym − Lym ˙Lx ϕ˙ t − Lx − Lym . (72 ) k=1 k m=1 m=1 k=1 k k=1 k m=1](article595x.gif)
![[x1x2 ...xn,y1y2...yn ] = 0 , (73 )](article605x.gif)
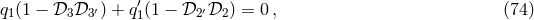


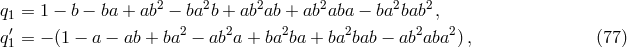
![Δ = [ab2a, ba2b]. (78 )](article642x.gif)