2 Physical and Historical Motivations of TDI
Equal-arm interferometer detectors of gravitational waves can observe gravitational radiation by canceling the laser frequency fluctuations affecting the light injected into their arms. This is done by comparing phases of split beams propagated along the equal (but non-parallel) arms of the detector. The laser frequency fluctuations affecting the two beams experience the same delay within the two equal-length arms and cancel out at the photodetector where relative phases are measured. This way gravitational-wave signals of dimensionless amplitude less than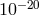 can be
observed when using lasers whose frequency stability can be as large as roughly a few parts in
can be
observed when using lasers whose frequency stability can be as large as roughly a few parts in
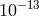 .
.
If the arms of the interferometer have different lengths, however, the exact cancellation of the laser
frequency fluctuations, say 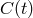 , will no longer take place at the photodetector. In fact, the larger the
difference between the two arms, the larger will be the magnitude of the laser frequency fluctuations
affecting the detector response. If
, will no longer take place at the photodetector. In fact, the larger the
difference between the two arms, the larger will be the magnitude of the laser frequency fluctuations
affecting the detector response. If 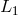 and
and 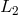 are the lengths of the two arms, it is easy to see that the
amount of laser relative frequency fluctuations remaining in the response is equal to (units in which the
speed of light
are the lengths of the two arms, it is easy to see that the
amount of laser relative frequency fluctuations remaining in the response is equal to (units in which the
speed of light 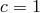 )
)
 in the mHz band, and whose arms will differ by a few
percent [5*, 13, 35], Eq. (1*) implies the following expression for the amplitude of the Fourier components of
the uncanceled laser frequency fluctuations (an over-imposed tilde denotes the operation of Fourier
transform):
At
in the mHz band, and whose arms will differ by a few
percent [5*, 13, 35], Eq. (1*) implies the following expression for the amplitude of the Fourier components of
the uncanceled laser frequency fluctuations (an over-imposed tilde denotes the operation of Fourier
transform):
At 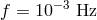 , for instance, and assuming
, for instance, and assuming 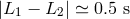 , the uncanceled fluctuations from the
laser are equal to
, the uncanceled fluctuations from the
laser are equal to  . Since the LISA sensitivity goal was about
. Since the LISA sensitivity goal was about 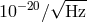 in this part
of the frequency band, it is clear that an alternative experimental approach for canceling the laser frequency
fluctuations is needed.
in this part
of the frequency band, it is clear that an alternative experimental approach for canceling the laser frequency
fluctuations is needed.
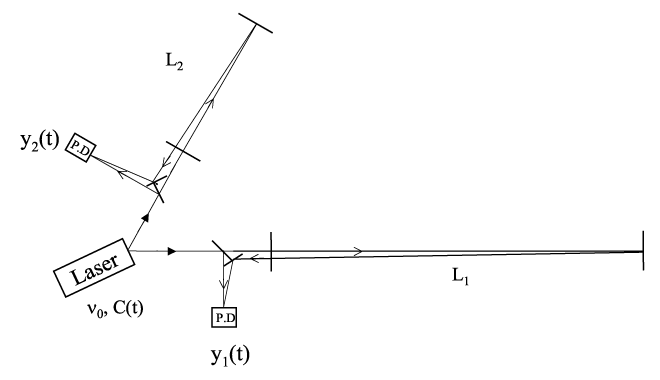
A first attempt to solve this problem was presented by Faller et al. [17*, 19, 18], and the scheme proposed there can be understood through Figure 1*. In this idealized model the two beams exiting the two arms are not made to interfere at a common photodetector. Rather, each is made to interfere with the incoming light from the laser at a photodetector, decoupling in this way the phase fluctuations experienced by the two beams in the two arms. Now two Doppler measurements are available in digital form, and the problem now becomes one of identifying an algorithm for digitally canceling the laser frequency fluctuations from a resulting new data combination.
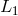 and
and 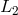 , are different, now the light
beams from the two arms are not recombined at one photo detector. Instead each is separately made
to interfere with the light that is injected into the arms. Two distinct photo detectors are now used,
and phase (or frequency) fluctuations are then monitored and recorded there.
, are different, now the light
beams from the two arms are not recombined at one photo detector. Instead each is separately made
to interfere with the light that is injected into the arms. Two distinct photo detectors are now used,
and phase (or frequency) fluctuations are then monitored and recorded there. The algorithm they first proposed, and refined subsequently in [24], required processing
the two Doppler measurements, say 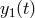 and
and 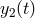 , in the Fourier domain. If we denote
with
, in the Fourier domain. If we denote
with 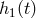 ,
, 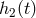 the gravitational-wave signals entering into the Doppler data
the gravitational-wave signals entering into the Doppler data 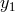 ,
,  ,
respectively, and with
,
respectively, and with 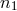 ,
, 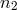 any other remaining noise affecting
any other remaining noise affecting 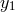 and
and 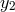 , respectively, then
the expressions for the Doppler observables
, respectively, then
the expressions for the Doppler observables 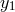 ,
,  can be written in the following form:
can be written in the following form:
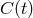 in the Doppler responses
in the Doppler responses 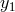 ,
, 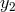 . The time signature of the noise
. The time signature of the noise 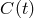 in
in  , for instance,
can be understood by observing that the frequency of the signal received at time
, for instance,
can be understood by observing that the frequency of the signal received at time  contains laser
frequency fluctuations transmitted
contains laser
frequency fluctuations transmitted 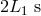 earlier. By subtracting from the frequency of the received signal
the frequency of the signal transmitted at time
earlier. By subtracting from the frequency of the received signal
the frequency of the signal transmitted at time 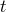 , we also subtract the frequency fluctuations
, we also subtract the frequency fluctuations  with
the net result shown in Eq. (3*).
with
the net result shown in Eq. (3*).
The algorithm for canceling the laser noise in the Fourier domain suggested in [17] works as follows. If
we take an infinitely long Fourier transform of the data 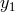 , the resulting expression of
, the resulting expression of 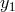 in the Fourier
domain becomes (see Eq. (3*))
in the Fourier
domain becomes (see Eq. (3*))
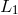 is known exactly, we can use the
is known exactly, we can use the 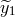 data to estimate the laser frequency
fluctuations
data to estimate the laser frequency
fluctuations 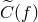 . This can be done by dividing
. This can be done by dividing 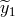 by the transfer function of the laser noise
by the transfer function of the laser noise 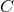 into the observable
into the observable  itself. By then further multiplying
itself. By then further multiplying ![^y ∕[e4πifL1 − 1] 1](article77x.gif) by the transfer
function of the laser noise into the other observable
by the transfer
function of the laser noise into the other observable 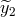 , i.e.,
, i.e., ![4πifL2 [e − 1]](article79x.gif) , and then subtract
the resulting expression from
, and then subtract
the resulting expression from 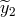 one accomplishes the cancellation of the laser frequency
fluctuations.
one accomplishes the cancellation of the laser frequency
fluctuations.
The problem with this procedure is the underlying assumption of being able to take an infinitely long
Fourier transform of the data. Even if one neglects the variation in time of the LISA arms, by taking a
finite-length Fourier transform of, say,  over a time interval
over a time interval 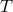 , the resulting transfer function
of the laser noise
, the resulting transfer function
of the laser noise 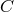 into
into 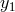 no longer will be equal to
no longer will be equal to ![[e4πifL1 − 1]](article85x.gif) . This can be seen
by writing the expression of the finite length Fourier transform of
. This can be seen
by writing the expression of the finite length Fourier transform of 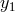 in the following way:
in the following way:
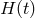 the function that is equal to 1 in the interval
the function that is equal to 1 in the interval ![[− T, +T ]](article89x.gif) , and zero
everywhere else. Eq. (6*) implies that the finite-length Fourier transform
, and zero
everywhere else. Eq. (6*) implies that the finite-length Fourier transform 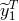 of
of 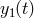 is equal to the
convolution in the Fourier domain of the infinitely long Fourier transform of
is equal to the
convolution in the Fourier domain of the infinitely long Fourier transform of 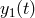 ,
, 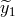 , with the Fourier
transform of
, with the Fourier
transform of 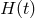 [28] (i.e., the “Sinc Function” of width
[28] (i.e., the “Sinc Function” of width 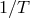 ). The key point here is that we can
no longer use the transfer function
). The key point here is that we can
no longer use the transfer function ![[e4πifLi − 1]](article96x.gif) ,
, 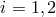 , for estimating the laser noise
fluctuations from one of the measured Doppler data, without retaining residual laser noise into the
combination of the two Doppler data
, for estimating the laser noise
fluctuations from one of the measured Doppler data, without retaining residual laser noise into the
combination of the two Doppler data  ,
, 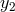 valid in the case of infinite integration time. The
amount of residual laser noise remaining in the Fourier-based combination described above, as a
function of the integration time
valid in the case of infinite integration time. The
amount of residual laser noise remaining in the Fourier-based combination described above, as a
function of the integration time 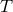 and type of “window function” used, was derived in the
appendix of [53*]. There it was shown that, in order to suppress the residual laser noise below
the LISA sensitivity level identified by secondary noises (such as proof-mass and optical path
noises) with the use of the Fourier-based algorithm an integration time of about six months was
needed.
and type of “window function” used, was derived in the
appendix of [53*]. There it was shown that, in order to suppress the residual laser noise below
the LISA sensitivity level identified by secondary noises (such as proof-mass and optical path
noises) with the use of the Fourier-based algorithm an integration time of about six months was
needed.
A solution to this problem was suggested in [53*], which works entirely in the time-domain. From
Eqs. (3*) and (4*) we may notice that, by taking the difference of the two Doppler data 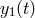 ,
,  ,
the frequency fluctuations of the laser now enter into this new data set in the following way:
,
the frequency fluctuations of the laser now enter into this new data set in the following way:
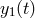 by the
round trip light time in arm 2,
by the
round trip light time in arm 2, 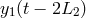 , and subtract from it the data
, and subtract from it the data 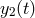 after it has been
time-shifted by the round trip light time in arm 1,
after it has been
time-shifted by the round trip light time in arm 1,  , we obtain the following data set:
In other words, the laser frequency fluctuations enter into
, we obtain the following data set:
In other words, the laser frequency fluctuations enter into  and
and  with the same time structure. This implies that, by subtracting Eq. (8*) from Eq. (7*) we can generate a new
data set that does not contain the laser frequency fluctuations
with the same time structure. This implies that, by subtracting Eq. (8*) from Eq. (7*) we can generate a new
data set that does not contain the laser frequency fluctuations 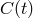 ,
The expression above of the
,
The expression above of the 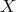 combination shows that it is possible to cancel the laser frequency noise in
the time domain by properly time-shifting and linearly combining Doppler measurements recorded by
different Doppler readouts. This in essence is what TDI amounts to.
combination shows that it is possible to cancel the laser frequency noise in
the time domain by properly time-shifting and linearly combining Doppler measurements recorded by
different Doppler readouts. This in essence is what TDI amounts to.
In order to gain a better physical understanding of how TDI works, let’s rewrite the above 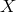 combination in the following form
combination in the following form
Equation (10*) shows that 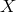 is the difference of two sums of relative frequency changes, each
corresponding to a specific light path (the continuous and dashed lines in Figure 2*). The continuous line,
corresponding to the first square-bracket term in Eq. (10*), represents a light-beam transmitted from
spacecraft 1 and made to bounce once at spacecraft 3 and 2 respectively. Since the other beam (dashed
line) experiences the same overall delay as the first beam (although by bouncing off spacecraft 2 first and
then spacecraft 3) when they are recombined they will cancel the laser phase fluctuations exactly, having
both experienced the same total delays (assuming stationary spacecraft). For this reason the combination
is the difference of two sums of relative frequency changes, each
corresponding to a specific light path (the continuous and dashed lines in Figure 2*). The continuous line,
corresponding to the first square-bracket term in Eq. (10*), represents a light-beam transmitted from
spacecraft 1 and made to bounce once at spacecraft 3 and 2 respectively. Since the other beam (dashed
line) experiences the same overall delay as the first beam (although by bouncing off spacecraft 2 first and
then spacecraft 3) when they are recombined they will cancel the laser phase fluctuations exactly, having
both experienced the same total delays (assuming stationary spacecraft). For this reason the combination
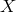 can be regarded as a synthesized (via TDI) zero-area Sagnac interferometer, with each beam
experiencing a delay equal to
can be regarded as a synthesized (via TDI) zero-area Sagnac interferometer, with each beam
experiencing a delay equal to 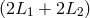 . In reality, there are only two beams in each arm (one in each
direction) and the lines in Figure 2* represent the paths of relative frequency changes rather than paths of
distinct light beams.
. In reality, there are only two beams in each arm (one in each
direction) and the lines in Figure 2* represent the paths of relative frequency changes rather than paths of
distinct light beams.
In the following sections we will further elaborate and generalize TDI to the realistic LISA configuration.

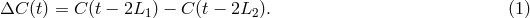
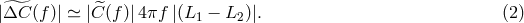

![[ 4πifL ] ^y1(f) = ^C (f) e 1 − 1 + ^h1(f ) + ^n1(f ). (5 )](article70x.gif)
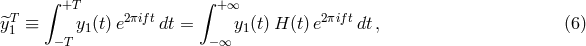
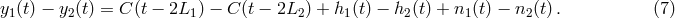
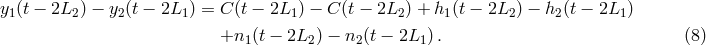
![X ≡ [y1(t) − y2(t)] − [y1(t − 2L2 ) − y2(t − 2L1)]. (9 )](article112x.gif)
![X = [y1(t) + y2(t − 2L1 )] − [y2(t) + y1(t − 2L2)], (10 )](article115x.gif)
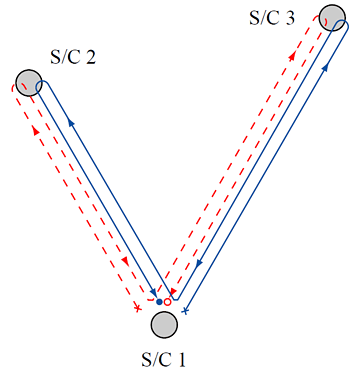
 , showing that it is a synthesized zero-area Sagnac
interferometer. The optical path begins at an “x” and the measurement is made at an “o”.
, showing that it is a synthesized zero-area Sagnac
interferometer. The optical path begins at an “x” and the measurement is made at an “o”.