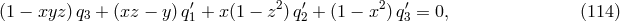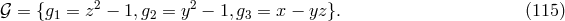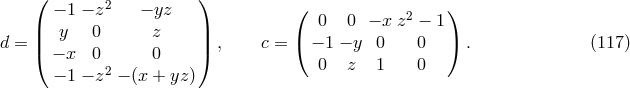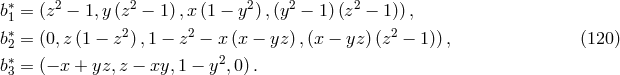A Generators of the Module of Syzygies
We require the 4-tuple solutions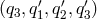 to the equation
where for convenience we have substituted
to the equation
where for convenience we have substituted 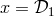 ,
, 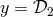 ,
, 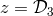 .
. 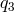 ,
, 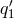 ,
, 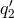 ,
, 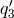 are
polynomials in
are
polynomials in 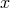 ,
, 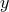 ,
,  with integral coefficients, i.e., in
with integral coefficients, i.e., in ![Z [x, y,z]](article1014x.gif) .
.
We now follow the procedure in the book by Becker et al. [3].
Consider the ideal in ![Z[x,y,z ]](article1015x.gif) (or
(or ![𝒬 [x, y,z]](article1016x.gif) where
where 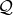 denotes the field of rational numbers),
formed by taking linear combinations of the coefficients in Eq. (114*),
denotes the field of rational numbers),
formed by taking linear combinations of the coefficients in Eq. (114*), 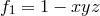 ,
, 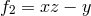 ,
,
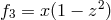 ,
, 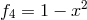 . A Gröbner basis for this ideal is
. A Gröbner basis for this ideal is
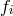 ,
, 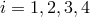 , and
, and 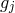 ,
, 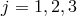 , generate the same ideal because we can express
one generating set in terms of the other and vice-versa:
where
, generate the same ideal because we can express
one generating set in terms of the other and vice-versa:
where 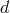 and
and  are
are 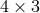 and
and 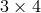 polynomial matrices, respectively, and are given by
The generators of the 4-tuple module are given by the set
polynomial matrices, respectively, and are given by
The generators of the 4-tuple module are given by the set 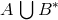 , where
, where  and
and 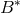 are the sets
described below:
are the sets
described below:
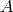 is the set of row vectors of the matrix
is the set of row vectors of the matrix 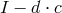 where the dot denotes the matrix product and
where the dot denotes the matrix product and 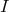 is the identity matrix,
is the identity matrix,  in our case. Thus,
in our case. Thus,
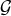 . The S-polynomial of two polynomials
. The S-polynomial of two polynomials 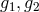 is obtained by multiplying
is obtained by multiplying 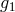 and
and
 by suitable terms and then adding, so that the highest terms cancel. For example in our case
by suitable terms and then adding, so that the highest terms cancel. For example in our case
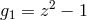 and
and 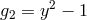 , and the highest terms are
, and the highest terms are  for
for  and
and 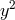 for
for 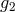 . Multiply
. Multiply
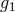 by
by 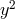 and
and 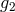 by
by 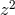 and subtract. Thus, the S-polynomial
and subtract. Thus, the S-polynomial 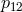 of
of  and
and 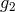 is
Note that order is defined (
is
Note that order is defined (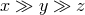 ) and the
) and the 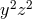 term cancels. For the Gröbner basis of 3 elements
we get 3 S-polynomials
term cancels. For the Gröbner basis of 3 elements
we get 3 S-polynomials 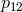 ,
, 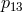 ,
, 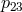 . The
. The 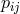 must now be re-expressed in terms of the Gröbner
basis
must now be re-expressed in terms of the Gröbner
basis 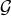 . This gives a
. This gives a 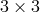 matrix
matrix  . The final step is to transform to four-tuples by multiplying
. The final step is to transform to four-tuples by multiplying 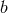 by the matrix
by the matrix  to obtain
to obtain 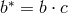 . The row vectors
. The row vectors 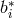 ,
, 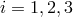 , of
, of  form the set
form the set  :
Thus, we obtain three more generators, which gives us a total of seven generators of the required module of
syzygies.
:
Thus, we obtain three more generators, which gives us a total of seven generators of the required module of
syzygies.