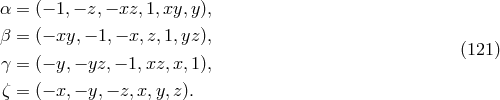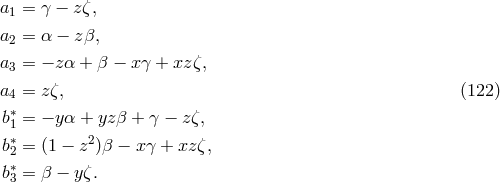B Conversion between Generating Sets
We list the three sets of generators and relations among them. We first list below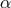 ,
, 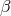 ,
, 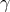 ,
, 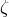 :
We now express the
:
We now express the 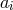 and
and 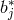 in terms of
in terms of 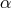 ,
,  ,
, 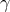 ,
, 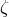 :
Further, we also list below
:
Further, we also list below 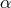 ,
, 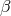 ,
, 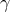 ,
, 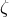 in terms of
in terms of 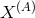 :
This proves that since the
:
This proves that since the 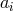 ,
, 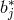 generate the required module, the
generate the required module, the 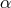 ,
, 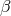 ,
,  ,
, 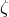 and
and 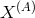 ,
,
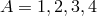 , also generate the same module.
, also generate the same module.
The Gröbner basis is given in terms of the above generators as follows:  ,
,  ,
,
 ,
, 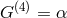 , and
, and  .
.