8 Concluding Remarks

In this article we have summarized the use of TDI for canceling the laser phase noise from heterodyne phase measurements performed by a constellation of three spacecraft tracking each other along arms of unequal length. Underlying the TDI technique is the mathematical structure of the theory of Gröbner basis and the algebra of modules over polynomial rings. These methods have been motivated and illustrated with the simple example of an unequal-arm interferometer in order to give a physical insight of TDI. Here, these methods have been rigorously applied to the idealized case of a stationary interferometer such as the LISA mission. This allowed us to derive the generators of the module from which the entire TDI data set can be obtained; they can be extended in a straight-forward way to more than three spacecraft for possible future mission concepts. The stationary LISA case was used as a propaedeutical introduction to the physical motivation of TDI, and for further extending it to the realistic LISA configuration of free-falling spacecraft orbiting around the Sun. The TDI data combinations canceling laser phase noise in this general case are referred to as second-generation TDI, and they contain twice as many terms as their corresponding first-generation combinations valid for the stationary configuration.

As a data analysis application we have shown that it is possible to identify specific TDI combinations that will allow LISA to achieve optimal sensitivity to gravitational radiation [38, 40, 39]. The resulting improvement in sensitivity over that of an unequal-arm Michelson interferometer, in the case of monochromatic signals randomly distributed over the celestial sphere and of random polarization, is non-negligible. 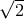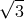We have found this to be equal to a factor of in the low-part of the frequency band, and slightly more than in the high-part of the LISA band. The SNR for binaries whose location in the sky is known, but their polarization is not, can also be optimized, and the degree of improvement depends on the location of the source in the sky.

We also addressed several experimental aspects of TDI, and emphasized that it has already been successfully tested experimentally [8, 32, 48, 33].

As of the writing of this second edition of our living review article, it is very gratifying to see how much TDI has matured since the publishing of its first version. The purpose of this second edition review of TDI was to provide the basic mathematical tools and knowledge of the current experimental results needed for working on future TDI projects. We hope to have accomplished this goal, and that others will be stimulated to work in this fascinating field of research.