List of Tables
| Table 1:
Numerically determined value of the 3PN coefficient for the SF part of the redshift observable defined by Eq. (292). The analytic post-Newtonian computation [68] is confirmed with many significant digits. |
| Table 2:
Numerically determined values of higher-order PN coefficients for the SF part of the redshift observable defined by Eq. (292). The uncertainty in the last digit (or two last digits) is indicated in parentheses. The 4PN numerical value agrees with the analytical expression (293*). |
| Table 3:
Post-Newtonian contributions to the accumulated number of gravitational-wave cycles 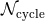 for compact binaries detectable in the bandwidth of LIGO-VIRGO detectors. The entry
frequency is for compact binaries detectable in the bandwidth of LIGO-VIRGO detectors. The entry
frequency is 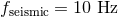 and the terminal frequency is and the terminal frequency is 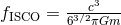 . The main origin of
the approximation (instantaneous vs. tail) is indicated. See also Table 4 in Section 11 below for the
contributions of spin-orbit effects. . The main origin of
the approximation (instantaneous vs. tail) is indicated. See also Table 4 in Section 11 below for the
contributions of spin-orbit effects. |
| Table 4:
Spin-orbit contributions to the number of gravitational-wave cycles 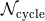 [defined by
Eq. (319*)] for binaries detectable by ground-based detectors LIGO-VIRGO. The entry frequency
is [defined by
Eq. (319*)] for binaries detectable by ground-based detectors LIGO-VIRGO. The entry frequency
is 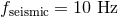 and the terminal frequency is and the terminal frequency is 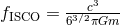 . For each compact object
the magnitude . For each compact object
the magnitude 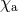 and the orientation and the orientation 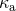 of the spin are defined by of the spin are defined by 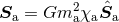 and and
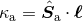 ; remind Eq. (366*). The spin-spin (SS) terms are neglected. ; remind Eq. (366*). The spin-spin (SS) terms are neglected. |
