6 Regularization of the Field of Point Particles
Our aim is to compute the metric (and its gradient needed in the equations of motion) at the 3PN order (say) for a system of two point-like particles. A priori one is not allowed to use directly some metric expressions like Eqs. (144) above, which have been derived under the assumption of a continuous (smooth) matter distribution. Applying them to a system of point particles, we find that most of the integrals become divergent at the location of the particles, i.e., when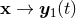 or
or 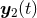 , where
, where 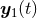 and
and 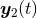 denote the two trajectories. Consequently, we must supplement the calculation by a prescription for how to
remove the infinite part of these integrals. At this stage different choices for a “self-field” regularization
(which will take care of the infinite self-field of point particles) are possible. In this section we review
the:
denote the two trajectories. Consequently, we must supplement the calculation by a prescription for how to
remove the infinite part of these integrals. At this stage different choices for a “self-field” regularization
(which will take care of the infinite self-field of point particles) are possible. In this section we review
the:
- Hadamard self-field regularization, which has proved to be very convenient for doing practical computations (in particular, by computer), but suffers from the important drawback of yielding some ambiguity parameters, which cannot be determined within this regularization, starting essentially at the 3PN order;
- Dimensional self-field regularization, an extremely powerful regularization which is free of any
ambiguities (at least up to the 3PN level), and therefore permits to uniquely fix the values
of the ambiguity parameters coming from Hadamard’s regularization. However, dimensional
regularization has not yet been implemented to the present problem in the general case (i.e.,
for an arbitrary space dimension
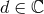 ).
).
The why and how the final results are unique and independent of the employed self-field regularization (in agreement with the physical expectation) stems from the effacing principle of general relativity [142*] – namely that the internal structure of the compact bodies makes a contribution only at the formal 5PN approximation. However, we shall review several alternative computations, independent of the self-field regularization, which confirm the end results.
6.1 Hadamard self-field regularization
In most practical computations we employ the Hadamard regularization [236, 381*] (see Ref. [382] for an entry to the mathematical literature). Let us present here an account of this regularization, as well as a theory of generalized functions (or pseudo-functions) associated with it, following the detailed investigations in Refs. [70*, 72*].
Consider the class 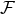 of functions
of functions 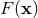 which are smooth (
which are smooth (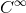 ) on
) on 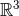 except for the
two points
except for the
two points 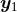 and
and 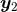 , around which they admit a power-like singular expansion of the
type:39
, around which they admit a power-like singular expansion of the
type:39
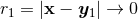 , and the coefficients
, and the coefficients  of the various
powers of
of the various
powers of 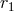 depend on the unit direction
depend on the unit direction 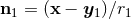 of approach to the singular point. The
powers
of approach to the singular point. The
powers  of
of 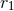 are real, range in discrete steps [i.e.,
are real, range in discrete steps [i.e., 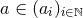 ], and are bounded from below
(
], and are bounded from below
(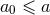 ). The coefficients
). The coefficients 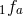 (and
(and 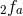 ) for which
) for which 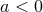 can be referred to as the singular
coefficients of
can be referred to as the singular
coefficients of  . If
. If  and
and  belong to
belong to  so does the ordinary product
so does the ordinary product 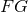 , as well as the
ordinary gradient
, as well as the
ordinary gradient 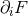 . We define the Hadamard partie finie of
. We define the Hadamard partie finie of 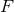 at the location of the point 1 where it
is singular as
where
at the location of the point 1 where it
is singular as
where 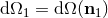 denotes the solid angle element centered on
denotes the solid angle element centered on 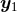 and of direction
and of direction 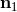 . Notice that
because of the angular integration in Eq. (160*), the Hadamard partie finie is “non-distributive” in the sense
that
The non-distributivity of Hadamard’s partie finie is the main source of the appearance of ambiguity
parameters at the 3PN order, as discussed in Section 6.2.
. Notice that
because of the angular integration in Eq. (160*), the Hadamard partie finie is “non-distributive” in the sense
that
The non-distributivity of Hadamard’s partie finie is the main source of the appearance of ambiguity
parameters at the 3PN order, as discussed in Section 6.2.
The second notion of Hadamard partie finie (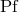 ) concerns that of the integral
) concerns that of the integral 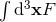 , which is
generically divergent at the location of the two singular points
, which is
generically divergent at the location of the two singular points 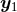 and
and 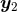 (we assume that the integral
converges at infinity). It is defined by
(we assume that the integral
converges at infinity). It is defined by
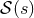 defined as
defined as 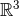 from which the two spherical balls
from which the two spherical balls 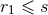 and
and 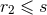 of radius
of radius  and centered on the two singularities, denoted
and centered on the two singularities, denoted 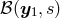 and
and 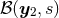 , are
excised:
, are
excised: 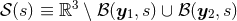 . The other terms, where the value of a function at point 1 takes
the meaning (160*), are precisely such that they cancel out the divergent part of the first term in the limit
where
. The other terms, where the value of a function at point 1 takes
the meaning (160*), are precisely such that they cancel out the divergent part of the first term in the limit
where 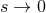 (the symbol
(the symbol 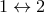 means the same terms but corresponding to the other point 2). The
Hadamard partie-finie integral depends on two strictly positive constants
means the same terms but corresponding to the other point 2). The
Hadamard partie-finie integral depends on two strictly positive constants 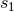 and
and 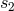 , associated with
the logarithms present in Eq. (162*). We shall look for the fate of these constants in the final
equations of motion and radiation field. See Ref. [70*] for alternative expressions of the partie-finie
integral.
, associated with
the logarithms present in Eq. (162*). We shall look for the fate of these constants in the final
equations of motion and radiation field. See Ref. [70*] for alternative expressions of the partie-finie
integral.
We now come to a specific variant of Hadamard’s regularization called the extended Hadamard
regularization (EHR) and defined in Refs. [70*, 72*]. The basic idea is to associate to any 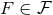 a
pseudo-function, called the partie finie pseudo-function
a
pseudo-function, called the partie finie pseudo-function 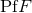 , namely a linear form acting on functions
, namely a linear form acting on functions
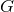 of
of 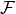 , and which is defined by the duality bracket
, and which is defined by the duality bracket
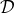 of smooth functions, i.e.,
of smooth functions, i.e., 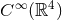 , with compact support (obviously we
have
, with compact support (obviously we
have 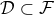 ), the pseudo-function
), the pseudo-function 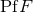 is a distribution in the sense of Schwartz [381*]. The
product of pseudo-functions coincides, by definition, with the ordinary point-wise product, namely
is a distribution in the sense of Schwartz [381*]. The
product of pseudo-functions coincides, by definition, with the ordinary point-wise product, namely
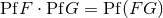 . In practical computations, we use an interesting pseudo-function, constructed on
the basis of the Riesz delta function [365], which plays a role analogous to the Dirac measure in
distribution theory,
. In practical computations, we use an interesting pseudo-function, constructed on
the basis of the Riesz delta function [365], which plays a role analogous to the Dirac measure in
distribution theory, 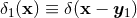 . This is the delta-pseudo-function
. This is the delta-pseudo-function 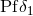 defined by
where
defined by
where 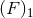 is the partie finie of
is the partie finie of 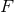 as given by Eq. (160*). From the product of
as given by Eq. (160*). From the product of 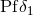 with any
with any 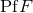 we obtain the new pseudo-function
we obtain the new pseudo-function 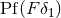 , that is such that
As a general rule, we are not allowed, in consequence of the “non-distributivity” of the Hadamard partie
finie, Eq. (161*), to replace
, that is such that
As a general rule, we are not allowed, in consequence of the “non-distributivity” of the Hadamard partie
finie, Eq. (161*), to replace 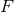 within the pseudo-function
within the pseudo-function 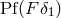 by its regularized value:
by its regularized value:
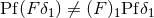 in general. It should be noticed that the object
in general. It should be noticed that the object 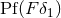 has no equivalent in
distribution theory.
has no equivalent in
distribution theory.
Next, we treat the spatial derivative of a pseudo-function of the type 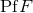 , namely
, namely 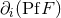 .
Essentially, we require [70*] that the rule of integration by parts holds. By this we mean that we are allowed
to freely operate by parts any duality bracket, with the all-integrated (“surface”) terms always being zero,
as in the case of non-singular functions. This requirement is motivated by our will that a computation
involving singular functions be as much as possible the same as if we were dealing with regular functions.
Thus, by definition,
.
Essentially, we require [70*] that the rule of integration by parts holds. By this we mean that we are allowed
to freely operate by parts any duality bracket, with the all-integrated (“surface”) terms always being zero,
as in the case of non-singular functions. This requirement is motivated by our will that a computation
involving singular functions be as much as possible the same as if we were dealing with regular functions.
Thus, by definition,
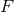 vanish, the derivative of
vanish, the derivative of 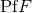 reduces to the ordinary derivative, i.e.,
reduces to the ordinary derivative, i.e., 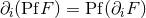 . Then it is trivial to check that the rule (166*)
contains as a particular case the standard definition of the distributional derivative [381*]. Notably, we see
that the integral of a gradient is always zero:
. Then it is trivial to check that the rule (166*)
contains as a particular case the standard definition of the distributional derivative [381*]. Notably, we see
that the integral of a gradient is always zero: 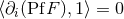 . This should certainly be the case if we
want to compute a quantity like a Hamiltonian density which is defined only modulo a total divergence. We
pose
where
. This should certainly be the case if we
want to compute a quantity like a Hamiltonian density which is defined only modulo a total divergence. We
pose
where 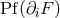 represents the “ordinary” derivative and
represents the “ordinary” derivative and ![Di [F ]](article1303x.gif) is the distributional term. The following
solution of the basic relation (166*) was obtained in Ref. [70*]:
where for simplicity we assume that the powers
is the distributional term. The following
solution of the basic relation (166*) was obtained in Ref. [70*]:
where for simplicity we assume that the powers  in the expansion (159*) of
in the expansion (159*) of 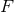 are relative integers. The
distributional term (168*) is of the form
are relative integers. The
distributional term (168*) is of the form 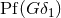 plus
plus 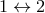 ; it is generated solely by the singular coefficients of
; it is generated solely by the singular coefficients of
 .40
The formula for the distributional term associated with the
.40
The formula for the distributional term associated with the 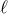 -th distributional derivative, i.e.
-th distributional derivative, i.e.
![DL [F ] = ∂LPfF − Pf ∂LF](article1313x.gif) , where
, where 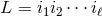 , reads
We refer to Theorem 4 in Ref. [70*] for the definition of another derivative operator,
representing the most general derivative satisfying the same properties as the one defined
by Eq. (168*), and, in addition, the commutation of successive derivatives (or Schwarz
lemma).41
, reads
We refer to Theorem 4 in Ref. [70*] for the definition of another derivative operator,
representing the most general derivative satisfying the same properties as the one defined
by Eq. (168*), and, in addition, the commutation of successive derivatives (or Schwarz
lemma).41
The distributional derivative defined by (167*) – (168*) does not satisfy the Leibniz rule for the derivation of a product, in accordance with a general result of Schwartz [380*]. Rather, the investigation of Ref. [70*] suggests that, in order to construct a consistent theory (using the ordinary point-wise product for pseudo-functions), the Leibniz rule should be weakened, and replaced by the rule of integration by part, Eq. (166*), which is in fact nothing but an integrated version of the Leibniz rule. However, the loss of the Leibniz rule stricto sensu constitutes one of the reasons for the appearance of the ambiguity parameters at 3PN order, see Section 6.2.
The Hadamard regularization 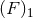 is defined by Eq. (160*) in a preferred spatial hypersurface
is defined by Eq. (160*) in a preferred spatial hypersurface
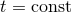 of a coordinate system, and consequently is not a priori compatible with the Lorentz
invariance. Thus we expect that the equations of motion in harmonic coordinates (which manifestly preserve
the global Lorentz invariance) should exhibit at some stage a violation of the Lorentz invariance due to the
latter regularization. In fact this occurs exactly at the 3PN order. Up to the 2.5PN level, the use of the
regularization
of a coordinate system, and consequently is not a priori compatible with the Lorentz
invariance. Thus we expect that the equations of motion in harmonic coordinates (which manifestly preserve
the global Lorentz invariance) should exhibit at some stage a violation of the Lorentz invariance due to the
latter regularization. In fact this occurs exactly at the 3PN order. Up to the 2.5PN level, the use of the
regularization 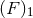 is sufficient to get some unambiguous equations of motion which are
Lorentz invariant [76*]. This problem can be dealt with within Hadamard’s regularization, by
introducing a Lorentz-invariant variant of this regularization, denoted
is sufficient to get some unambiguous equations of motion which are
Lorentz invariant [76*]. This problem can be dealt with within Hadamard’s regularization, by
introducing a Lorentz-invariant variant of this regularization, denoted ![[F ]1](article1319x.gif) in Ref. [72*]. It
consists of performing the Hadamard regularization within the spatial hypersurface that is
geometrically orthogonal (in a Minkowskian sense) to the four-velocity of the particle. The
regularization
in Ref. [72*]. It
consists of performing the Hadamard regularization within the spatial hypersurface that is
geometrically orthogonal (in a Minkowskian sense) to the four-velocity of the particle. The
regularization ![[F ]1](article1320x.gif) differs from the simpler regularization
differs from the simpler regularization 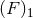 by relativistic corrections of order
by relativistic corrections of order
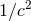 at least. See [72*] for the formulas defining this regularization in the form of some infinite
power series in
at least. See [72*] for the formulas defining this regularization in the form of some infinite
power series in 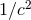 . The regularization
. The regularization ![[F]1](article1324x.gif) plays a crucial role in obtaining the equations
of motion at the 3PN order in Refs. [69*, 71*]. In particular, the use of the Lorentz-invariant
regularization
plays a crucial role in obtaining the equations
of motion at the 3PN order in Refs. [69*, 71*]. In particular, the use of the Lorentz-invariant
regularization ![[F ]1](article1325x.gif) permits to obtain the value of the ambiguity parameter
permits to obtain the value of the ambiguity parameter 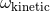 in Eq. (170a)
below.
in Eq. (170a)
below.
6.2 Hadamard regularization ambiguities
The standard Hadamard regularization yields some ambiguous results for the computation of certain
integrals at the 3PN order, as noticed by Jaranowski & Schäfer [261*, 262*, 263*] in their computation of
the equations of motion within the ADM-Hamiltonian formulation of general relativity. By standard
Hadamard regularization we mean the regularization based solely on the definitions of the partie finie of a
singular function, Eq. (160*), and the partie finie of a divergent integral, Eq. (162*), and without using a
theory of pseudo-functions and generalized distributional derivatives as in Refs. [70*, 72*]. It was shown in
Refs. [261*, 262*, 263*] that there are two and only two types of ambiguous terms in the 3PN
Hamiltonian, which were then parametrized by two unknown numerical coefficients called 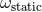 and
and
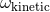 .
.
Progressing concurrently, Blanchet & Faye [70*, 72*] introduced the “extended” Hadamard regularization
– the one we outlined in Section 6.1 – and obtained [69*, 71*] the 3PN equations of motion complete except
for one and only one unknown numerical constant, called 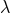 . The new extended Hadamard regularization
is mathematically well-defined and yields unique results for the computation of any integral in the
problem; however, it turned out to be in a sense “incomplete” as it could not determine the value
of this constant. The comparison of the result with the work [261*, 262*], on the basis of the
computation of the invariant energy of compact binaries moving on circular orbits, revealed [69*] that
. The new extended Hadamard regularization
is mathematically well-defined and yields unique results for the computation of any integral in the
problem; however, it turned out to be in a sense “incomplete” as it could not determine the value
of this constant. The comparison of the result with the work [261*, 262*], on the basis of the
computation of the invariant energy of compact binaries moving on circular orbits, revealed [69*] that
Therefore, the ambiguity 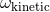 is fixed, while
is fixed, while 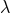 is equivalent to the other ambiguity
is equivalent to the other ambiguity 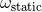 .
Notice that the value (170a) for the kinetic ambiguity parameter
.
Notice that the value (170a) for the kinetic ambiguity parameter 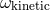 , which is in factor of some
velocity dependent terms, is the only one for which the 3PN equations of motion are Lorentz invariant.
Fixing up this value was possible because the extended Hadamard regularization [70*, 72*] was defined in
such a way that it keeps the Lorentz invariance.
, which is in factor of some
velocity dependent terms, is the only one for which the 3PN equations of motion are Lorentz invariant.
Fixing up this value was possible because the extended Hadamard regularization [70*, 72*] was defined in
such a way that it keeps the Lorentz invariance.
The value of 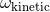 given by Eq. (170a) was recovered in Ref. [162*] by directly proving that such
value is the unique one for which the global Poincaré invariance of the ADM-Hamiltonian formalism is
verified. Since the coordinate conditions associated with the ADM formalism do not manifestly respect the
Poincaré symmetry, it was necessary to prove that the 3PN Hamiltonian is compatible with the existence
of generators for the Poincaré algebra. By contrast, the harmonic-coordinate conditions preserve the
Poincaré invariance, and therefore the associated equations of motion at 3PN order are manifestly
Lorentz-invariant, as was found to be the case in Refs. [69*, 71*].
given by Eq. (170a) was recovered in Ref. [162*] by directly proving that such
value is the unique one for which the global Poincaré invariance of the ADM-Hamiltonian formalism is
verified. Since the coordinate conditions associated with the ADM formalism do not manifestly respect the
Poincaré symmetry, it was necessary to prove that the 3PN Hamiltonian is compatible with the existence
of generators for the Poincaré algebra. By contrast, the harmonic-coordinate conditions preserve the
Poincaré invariance, and therefore the associated equations of motion at 3PN order are manifestly
Lorentz-invariant, as was found to be the case in Refs. [69*, 71*].
The appearance of one and only one physical unknown coefficient 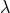 in the equations of motion
constitutes a quite striking fact, that is related specifically with the use of a Hadamard-type
regularization.42
Technically speaking, the presence of the ambiguity parameter
in the equations of motion
constitutes a quite striking fact, that is related specifically with the use of a Hadamard-type
regularization.42
Technically speaking, the presence of the ambiguity parameter 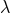 is associated with the non-distributivity
of Hadamard’s regularization, in the sense of Eq. (161*). Mathematically speaking,
is associated with the non-distributivity
of Hadamard’s regularization, in the sense of Eq. (161*). Mathematically speaking, 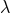 is probably related
to the fact that it is impossible to construct a distributional derivative operator, such as Eqs. (167*) – (168*),
satisfying the Leibniz rule for the derivation of the product [380]. The Einstein field equations can be
written in many different forms, by shifting the derivatives and operating some terms by parts with the help
of the Leibniz rule. All these forms are equivalent in the case of regular sources, but since the
derivative operator (167*) – (168*) violates the Leibniz rule they become inequivalent for point
particles.
is probably related
to the fact that it is impossible to construct a distributional derivative operator, such as Eqs. (167*) – (168*),
satisfying the Leibniz rule for the derivation of the product [380]. The Einstein field equations can be
written in many different forms, by shifting the derivatives and operating some terms by parts with the help
of the Leibniz rule. All these forms are equivalent in the case of regular sources, but since the
derivative operator (167*) – (168*) violates the Leibniz rule they become inequivalent for point
particles.
Physically speaking, let us also argue that 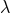 has its root in the fact that in a complete
computation of the equations of motion valid for two regular extended weakly self-gravitating bodies,
many non-linear integrals, when taken individually, start depending, from the 3PN order, on
the internal structure of the bodies, even in the “compact-body” limit where the radii tend to
zero. However, when considering the full equations of motion, one expects that all the terms
depending on the internal structure can be removed, in the compact-body limit, by a coordinate
transformation (or by some appropriate shifts of the central world lines of the bodies), and
that finally
has its root in the fact that in a complete
computation of the equations of motion valid for two regular extended weakly self-gravitating bodies,
many non-linear integrals, when taken individually, start depending, from the 3PN order, on
the internal structure of the bodies, even in the “compact-body” limit where the radii tend to
zero. However, when considering the full equations of motion, one expects that all the terms
depending on the internal structure can be removed, in the compact-body limit, by a coordinate
transformation (or by some appropriate shifts of the central world lines of the bodies), and
that finally 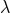 is given by a pure number, for instance a rational fraction, independent of the
details of the internal structure of the compact bodies. From this argument (which could be
justified by the effacing principle in general relativity) the value of
is given by a pure number, for instance a rational fraction, independent of the
details of the internal structure of the compact bodies. From this argument (which could be
justified by the effacing principle in general relativity) the value of 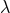 is necessarily the one
we compute below, Eq. (172*), and will be valid for any compact objects, for instance black
holes.
is necessarily the one
we compute below, Eq. (172*), and will be valid for any compact objects, for instance black
holes.
The ambiguity parameter 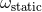 , which is in factor of some static, velocity-independent term, and
hence cannot be derived by invoking Lorentz invariance, was computed by Damour, Jaranowski &
Schäfer [163*] by means of dimensional regularization, instead of some Hadamard-type one, within the
ADM-Hamiltonian formalism. Their result is
, which is in factor of some static, velocity-independent term, and
hence cannot be derived by invoking Lorentz invariance, was computed by Damour, Jaranowski &
Schäfer [163*] by means of dimensional regularization, instead of some Hadamard-type one, within the
ADM-Hamiltonian formalism. Their result is
The ambiguity parameter 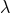 is fixed from the result (171*) and the necessary link (170b) provided by
the equivalence between the harmonic-coordinates and ADM-Hamiltonian formalisms [69*, 164]. However,
is fixed from the result (171*) and the necessary link (170b) provided by
the equivalence between the harmonic-coordinates and ADM-Hamiltonian formalisms [69*, 164]. However,
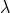 has also been computed directly by Blanchet, Damour & Esposito-Farèse [61*] applying dimensional
regularization to the 3PN equations of motion in harmonic coordinates (in the line of Refs. [69*, 71*]). The
end result,
has also been computed directly by Blanchet, Damour & Esposito-Farèse [61*] applying dimensional
regularization to the 3PN equations of motion in harmonic coordinates (in the line of Refs. [69*, 71*]). The
end result,
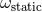 or
or 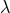 , the work [61*] provides also a
confirmation of the consistency of dimensional regularization, since the explicit calculations are entirely
different from the ones of Ref. [163*]: Harmonic coordinates instead of ADM-type ones, work at the level of
the equations of motion instead of the Hamiltonian, a different form of Einstein’s field equations which is
solved by a different iteration scheme.
, the work [61*] provides also a
confirmation of the consistency of dimensional regularization, since the explicit calculations are entirely
different from the ones of Ref. [163*]: Harmonic coordinates instead of ADM-type ones, work at the level of
the equations of motion instead of the Hamiltonian, a different form of Einstein’s field equations which is
solved by a different iteration scheme.
Let us comment that the use of a self-field regularization, be it dimensional or based on Hadamard’s
partie finie, signals a somewhat unsatisfactory situation on the physical point of view, because, ideally, we
would like to perform a complete calculation valid for extended bodies, taking into account
the details of the internal structure of the bodies (energy density, pressure, internal velocity
field, etc.). By considering the limit where the radii of the objects tend to zero, one should
recover the same result as obtained by means of the point-mass regularization. This would
demonstrate the suitability of the regularization. This program was undertaken at the 2PN
order in Refs. [280, 234] which derived the equations of motion of two extended fluid balls, and
obtained equations of motion depending only on the two masses 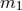 and
and 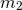 of the compact
bodies.44
At the 3PN order we expect that the extended-body program should give the value of the regularization
parameter
of the compact
bodies.44
At the 3PN order we expect that the extended-body program should give the value of the regularization
parameter 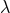 – probably after a coordinate transformation to remove the terms depending on the internal
structure. Ideally, its value should also be confirmed by independent and more physical methods like those
of Refs. [407, 281, 172].
– probably after a coordinate transformation to remove the terms depending on the internal
structure. Ideally, its value should also be confirmed by independent and more physical methods like those
of Refs. [407, 281, 172].
An important work, in several aspects more physical than the formal use of regularizations, is the one of
Itoh & Futamase [255*, 253*, 254*], following previous investigations in Refs. [256, 257]. These authors
derived the 3PN equations of motion in harmonic coordinates by means of a particular variant of the
famous “surface-integral” method à la Einstein, Infeld & Hoffmann [184]. The aim is to describe extended
relativistic compact binary systems in the so-called strong-field point particle limit which has been defined
in Ref. [212]. This approach is interesting because it is based on the physical notion of extended
compact bodies in general relativity, and is free of the problems of ambiguities. The end result of
Refs. [255*, 253*] is in agreement with the 3PN harmonic coordinates equations of motion [69*, 71*]
and is unambiguous, as it does directly determine the ambiguity parameter 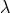 to exactly the
value (172*).
to exactly the
value (172*).
The 3PN equations of motion in harmonic coordinates or, more precisely, the associated 3PN
Lagrangian, were also derived by Foffa & Sturani [203] using another important approach, coined the
effective field theory (EFT) [223*]. Their result is fully compatible with the value (172*) for the ambiguity
parameter 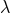 ; however, in contrast with the surface-integral method of Refs. [255, 253], this does not
check the method of regularization because the EFT approach is also based on dimensional self-field
regularization.
; however, in contrast with the surface-integral method of Refs. [255, 253], this does not
check the method of regularization because the EFT approach is also based on dimensional self-field
regularization.
We next consider the problem of the binary’s radiation field, where the same phenomenon occurs, with
the appearance of some Hadamard regularization ambiguity parameters at 3PN order. More
precisely, Blanchet, Iyer & Joguet [81*], computing the 3PN compact binary’s mass quadrupole
moment 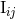 , found it necessary to introduce three Hadamard regularization constants
, found it necessary to introduce three Hadamard regularization constants 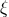 ,
,
 , and
, and 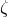 , which are independent of the equation-of-motion related constant
, which are independent of the equation-of-motion related constant 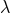 . The total
gravitational-wave flux at 3PN order, in the case of circular orbits, was found to depend on a single
combination of the latter constants,
. The total
gravitational-wave flux at 3PN order, in the case of circular orbits, was found to depend on a single
combination of the latter constants, 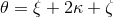 , and the binary’s orbital phase, for circular
orbits, involved only the linear combination of
, and the binary’s orbital phase, for circular
orbits, involved only the linear combination of 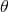 and
and 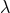 given by
given by 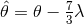 , as shown
in [73].
, as shown
in [73].
Dimensional regularization (instead of Hadamard’s) has next been applied in Refs. [62*, 63*] to the computation of the 3PN radiation field of compact binaries, leading to the following unique determination of the ambiguity parameters:45
These values represent the end result of dimensional regularization. However, several alternative
calculations provide a check, independent of dimensional regularization, for all the parameters (173). One
computes [80*] the 3PN binary’s mass dipole moment 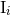 using Hadamard’s regularization, and identifies
using Hadamard’s regularization, and identifies
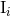 with the 3PN center of mass vector position
with the 3PN center of mass vector position 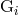 , already known as a conserved integral associated
with the Poincaré invariance of the 3PN equations of motion in harmonic coordinates [174*]. This yields
, already known as a conserved integral associated
with the Poincaré invariance of the 3PN equations of motion in harmonic coordinates [174*]. This yields
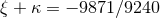 in agreement with Eqs. (173). Next, one considers [65] the limiting physical
situation where the mass of one of the particles is exactly zero (say,
in agreement with Eqs. (173). Next, one considers [65] the limiting physical
situation where the mass of one of the particles is exactly zero (say, 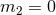 ), and the other particle moves
with uniform velocity. Technically, the 3PN quadrupole moment of a boosted Schwarzschild black hole is
computed and compared with the result for
), and the other particle moves
with uniform velocity. Technically, the 3PN quadrupole moment of a boosted Schwarzschild black hole is
computed and compared with the result for 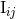 in the limit
in the limit 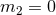 . The result is
. The result is 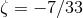 ,
and represents a direct verification of the global Poincaré invariance of the wave generation
formalism (the parameter
,
and represents a direct verification of the global Poincaré invariance of the wave generation
formalism (the parameter 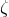 representing the analogue for the radiation field of the parameter
representing the analogue for the radiation field of the parameter
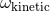 ). Finally, one proves [63*] that
). Finally, one proves [63*] that 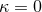 by showing that there are no dangerously divergent
diagrams corresponding to non-zero
by showing that there are no dangerously divergent
diagrams corresponding to non-zero  -values, where a diagram is meant here in the sense of
Ref. [151].
-values, where a diagram is meant here in the sense of
Ref. [151].
The determination of the parameters (173) completes the problem of the general relativistic prediction for the templates of inspiralling compact binaries up to 3.5PN order. The numerical values of these parameters indicate, following measurement-accuracy analyses [105*, 106*, 159*, 156*], that the 3.5PN order should provide an excellent approximation for both the on-line search and the subsequent off-line analysis of gravitational wave signals from inspiralling compact binaries in the LIGO and VIRGO detectors.
6.3 Dimensional regularization of the equations of motion
As reviewed in Section 6.2, work at 3PN order using Hadamard’s self-field regularization showed the
appearance of ambiguity parameters, due to an incompleteness of the Hadamard regularization employed
for curing the infinite self field of point particles. We give here more details on the determination using
dimensional regularization of the ambiguity parameter 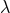 [or equivalently
[or equivalently 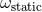 , see Eq. (170b)] which
appeared in the 3PN equations of motion.
, see Eq. (170b)] which
appeared in the 3PN equations of motion.
Dimensional regularization was invented as a means to preserve the gauge symmetry of perturbative
quantum field theories [391, 91, 100, 131]. Our basic problem here is to respect the gauge symmetry
associated with the diffeomorphism invariance of the classical general relativistic description of interacting
point masses. Hence, we use dimensional regularization not merely as a trick to compute some particular
integrals which would otherwise be divergent, but as a powerful tool for solving in a consistent way the
Einstein field equations with singular point-mass sources, while preserving its crucial symmetries. In
particular, we shall prove that dimensional regularization determines the kinetic ambiguity parameter
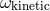 (and its radiation-field analogue
(and its radiation-field analogue 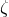 ), and is therefore able to correctly keep track of the global
Lorentz–Poincaré invariance of the gravitational field of isolated systems. The dimensional regularization is
also an important ingredient of the EFT approach to equations of motion and gravitational
radiation [223].
), and is therefore able to correctly keep track of the global
Lorentz–Poincaré invariance of the gravitational field of isolated systems. The dimensional regularization is
also an important ingredient of the EFT approach to equations of motion and gravitational
radiation [223].
The Einstein field equations in 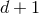 space-time dimensions, relaxed by the condition of harmonic
coordinates
space-time dimensions, relaxed by the condition of harmonic
coordinates 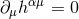 , take exactly the same form as given in Eqs. (18*) – (23*). In particular the box
operator
, take exactly the same form as given in Eqs. (18*) – (23*). In particular the box
operator  now denotes the flat space-time d’Alembertian operator in
now denotes the flat space-time d’Alembertian operator in 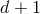 dimensions with signature
dimensions with signature
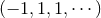 . The gravitational constant
. The gravitational constant 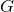 is related to the usual three-dimensional Newton’s constant
is related to the usual three-dimensional Newton’s constant
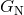 by
by
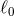 denotes an arbitrary length scale. The explicit expression of the gravitational source term
denotes an arbitrary length scale. The explicit expression of the gravitational source term 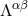 involves some
involves some 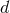 -dependent coefficients, and is given by
-dependent coefficients, and is given by
When 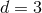 we recover Eq. (24). In the following we assume, as usual in dimensional regularization,
that the dimension of space is a complex number,
we recover Eq. (24). In the following we assume, as usual in dimensional regularization,
that the dimension of space is a complex number, 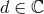 , and prove many results by invoking complex
analytic continuation in
, and prove many results by invoking complex
analytic continuation in 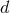 . We shall often pose
. We shall often pose 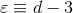 .
.
We parametrize the 3PN metric in 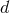 dimensions by means of some retarded potentials
dimensions by means of some retarded potentials 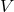 ,
, 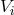 ,
,
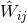 ,
, 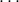 , which are straightforward
, which are straightforward 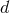 -dimensional generalizations of the potentials used in three
dimensions and which were defined in Section 5.3. Those are obtained by post-Newtonian iteration of the
-dimensional generalizations of the potentials used in three
dimensions and which were defined in Section 5.3. Those are obtained by post-Newtonian iteration of the
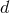 -dimensional field equations, starting from appropriate definitions of matter source densities generalizing
Eqs. (145):
-dimensional field equations, starting from appropriate definitions of matter source densities generalizing
Eqs. (145):
As a result all the expressions of Section 5.3 acquire some explicit 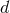 -dependent coefficients. For
instance we find [61*]
-dependent coefficients. For
instance we find [61*]
Here 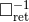 means the retarded integral in
means the retarded integral in 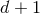 space-time dimensions, which
admits, though, no simple expression generalizing Eq. (31*) in physical
space-time dimensions, which
admits, though, no simple expression generalizing Eq. (31*) in physical 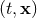 space.46
space.46
As reviewed in Section 6.1, the generic functions 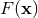 we have to deal with in 3 dimensions, are
smooth on
we have to deal with in 3 dimensions, are
smooth on 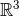 except at
except at 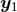 and
and 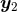 , around which they admit singular Laurent-type expansions in
powers and inverse powers of
, around which they admit singular Laurent-type expansions in
powers and inverse powers of 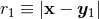 and
and 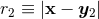 , given by Eq. (178*). In
, given by Eq. (178*). In 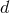 spatial
dimensions, there is an analogue of the function
spatial
dimensions, there is an analogue of the function 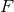 , which results from the post-Newtonian iteration
process performed in
, which results from the post-Newtonian iteration
process performed in 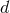 dimensions as we just outlined. Let us call this function
dimensions as we just outlined. Let us call this function 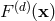 , where
, where
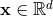 . When
. When 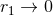 the function
the function 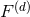 admits a singular expansion which is more involved than in 3
dimensions, as it reads
admits a singular expansion which is more involved than in 3
dimensions, as it reads
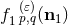 depend on
depend on 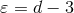 , and the powers of
, and the powers of 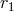 involve the relative integers
involve the relative integers 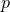 and
and 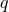 whose values are limited by some
whose values are limited by some 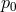 ,
, 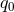 and
and 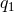 as indicated. Here we will be interested in
functions
as indicated. Here we will be interested in
functions 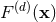 which have no poles as
which have no poles as 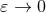 (this will always be the case at 3PN order).
Therefore, we can deduce from the fact that
(this will always be the case at 3PN order).
Therefore, we can deduce from the fact that 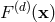 is continuous at
is continuous at 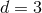 the constraint
the constraint
For the problem at hand, we essentially have to deal with the regularization of Poisson integrals, or
iterated Poisson integrals (and their gradients needed in the equations of motion), of the generic function
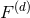 . The Poisson integral of
. The Poisson integral of 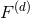 , in
, in 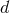 dimensions, is given by the Green’s function for the Laplace
operator,
dimensions, is given by the Green’s function for the Laplace
operator,
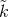 is a constant related to the usual Eulerian
is a constant related to the usual Eulerian 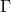 -function
by47
We need to evaluate the Poisson integral at the point
-function
by47
We need to evaluate the Poisson integral at the point 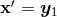 where it is singular; this is quite easy in
dimensional regularization, because the nice properties of analytic continuation allow simply to get
where it is singular; this is quite easy in
dimensional regularization, because the nice properties of analytic continuation allow simply to get
![[P (d)(x′)]x′=y 1](article1468x.gif) by replacing
by replacing 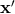 by
by 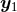 inside the explicit integral (180*). So we simply have
inside the explicit integral (180*). So we simply have
It is not possible at present to compute the equations of motion in the general 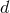 -dimensional case, but
only in the limit where
-dimensional case, but
only in the limit where 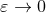 [163*, 61*]. The main technical step of our strategy consists of computing, in
the limit
[163*, 61*]. The main technical step of our strategy consists of computing, in
the limit 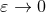 , the difference between the
, the difference between the 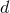 -dimensional Poisson potential (182*), and its Hadamard
3-dimensional counterpart given by
-dimensional Poisson potential (182*), and its Hadamard
3-dimensional counterpart given by 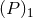 , where the Hadamard partie finie is defined by Eq. (160*). But
we must be precise when defining the Hadamard partie finie of a Poisson integral. Indeed, the
definition (160*) stricto sensu is applicable when the expansion of the function
, where the Hadamard partie finie is defined by Eq. (160*). But
we must be precise when defining the Hadamard partie finie of a Poisson integral. Indeed, the
definition (160*) stricto sensu is applicable when the expansion of the function 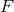 , for
, for 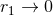 ,
does not involve logarithms of
,
does not involve logarithms of 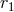 ; see Eq. (160*). However, the Poisson integral
; see Eq. (160*). However, the Poisson integral 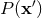 of
of
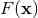 will typically involve such logarithms at the 3PN order, namely some
will typically involve such logarithms at the 3PN order, namely some 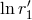 where
where
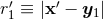 formally tends to zero (hence
formally tends to zero (hence 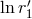 is formally infinite). The proper way to define the
Hadamard partie finie in this case is to include the
is formally infinite). The proper way to define the
Hadamard partie finie in this case is to include the 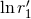 into its definition; we arrive at [70*]
into its definition; we arrive at [70*]
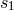 entering the partie finie integral (162*) has been “replaced” by
entering the partie finie integral (162*) has been “replaced” by
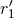 , which plays the role of a new regularization constant (together with
, which plays the role of a new regularization constant (together with 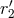 for the other particle), and
which ultimately parametrizes the final Hadamard regularized 3PN equations of motion. It was
shown that
for the other particle), and
which ultimately parametrizes the final Hadamard regularized 3PN equations of motion. It was
shown that 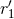 and
and 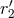 are unphysical, in the sense that they can be removed by a coordinate
transformation [69*, 71*]. On the other hand, the constant
are unphysical, in the sense that they can be removed by a coordinate
transformation [69*, 71*]. On the other hand, the constant 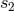 remaining in the result (183*) is the source
for the appearance of the physical ambiguity parameter
remaining in the result (183*) is the source
for the appearance of the physical ambiguity parameter 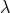 . Denoting the difference between the
dimensional and Hadamard regularizations by means of the script letter
. Denoting the difference between the
dimensional and Hadamard regularizations by means of the script letter 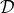 , we pose (for what concerns
the point 1)
That is,
, we pose (for what concerns
the point 1)
That is, 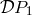 is what we shall have to add to the Hadamard-regularization result in order to get the
is what we shall have to add to the Hadamard-regularization result in order to get the
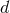 -dimensional result. However, we shall only compute the first two terms of the Laurent expansion of
-dimensional result. However, we shall only compute the first two terms of the Laurent expansion of
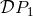 when
when 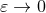 , say
, say 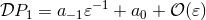 . This is the information we need to clear up the
ambiguity parameter. We insist that the difference
. This is the information we need to clear up the
ambiguity parameter. We insist that the difference 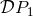 comes exclusively from the contribution of terms
developing some poles
comes exclusively from the contribution of terms
developing some poles 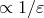 in the
in the 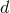 -dimensional calculation.
-dimensional calculation.
Next we outline the way we obtain, starting from the computation of the “difference”, the 3PN
equations of motion in dimensional regularization, and show how the ambiguity parameter 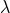 is
determined. By contrast to
is
determined. By contrast to 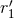 and
and 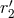 which are pure gauge,
which are pure gauge, 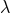 is a genuine physical ambiguity,
introduced in Refs. [70*, 71*] as the single unknown numerical constant parametrizing the ratio between
is a genuine physical ambiguity,
introduced in Refs. [70*, 71*] as the single unknown numerical constant parametrizing the ratio between 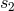 and
and 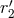 [where
[where 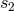 is the constant left in Eq. (183*)] as
is the constant left in Eq. (183*)] as
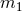 and
and 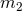 are the two masses. The terms corresponding to the
are the two masses. The terms corresponding to the 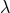 -ambiguity in the
acceleration
-ambiguity in the
acceleration 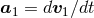 of particle 1 read simply
where the relative distance between particles is denoted
of particle 1 read simply
where the relative distance between particles is denoted 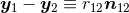 (with
(with 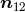 being the unit
vector pointing from particle 2 to particle 1). We start from the end result of Ref. [71*] for the 3PN
harmonic coordinates acceleration
being the unit
vector pointing from particle 2 to particle 1). We start from the end result of Ref. [71*] for the 3PN
harmonic coordinates acceleration 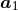 in Hadamard’s regularization, abbreviated as HR. Since the result
was obtained by means of the specific extended variant of Hadamard’s regularization (in short EHR, see
Section 6.1) we write it as
where
in Hadamard’s regularization, abbreviated as HR. Since the result
was obtained by means of the specific extended variant of Hadamard’s regularization (in short EHR, see
Section 6.1) we write it as
where 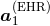 is a fully determined functional of the masses
is a fully determined functional of the masses 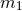 and
and 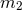 , the relative distance
, the relative distance
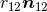 , the coordinate velocities
, the coordinate velocities 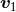 and
and 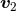 , and also the gauge constants
, and also the gauge constants 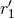 and
and 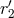 . The only
ambiguous term is the second one and is given by Eq. (186*).
. The only
ambiguous term is the second one and is given by Eq. (186*).
Our strategy is to extract from both the dimensional and Hadamard regularizations their common core
part, obtained by applying the so-called “pure-Hadamard–Schwartz” (pHS) regularization. Following the
definition in Ref. [61*], the pHS regularization is a specific, minimal Hadamard-type regularization of
integrals, based on the partie finie integral (162*), together with a minimal treatment of “contact” terms, in
which the definition (162*) is applied separately to each of the elementary potentials 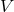 ,
, 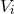 , etc. (and
gradients) that enter the post-Newtonian metric. Furthermore, the regularization of a product of these
potentials is assumed to be distributive, i.e.,
, etc. (and
gradients) that enter the post-Newtonian metric. Furthermore, the regularization of a product of these
potentials is assumed to be distributive, i.e., 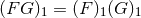 in the case where
in the case where 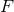 and
and 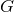 are given
by such elementary potentials; this is thus in contrast with Eq. (161*). The pHS regularization also
assumes the use of standard Schwartz distributional derivatives [381]. The interest of the pHS
regularization is that the dimensional regularization is equal to it plus the “difference”; see
Eq. (190*).
are given
by such elementary potentials; this is thus in contrast with Eq. (161*). The pHS regularization also
assumes the use of standard Schwartz distributional derivatives [381]. The interest of the pHS
regularization is that the dimensional regularization is equal to it plus the “difference”; see
Eq. (190*).
To obtain the pHS-regularized acceleration we need to substract from the EHR result a series of contributions, which are specific consequences of the use of EHR [70, 72]. For instance, one of these contributions corresponds to the fact that in the EHR the distributional derivative is given by Eqs. (167*) – (168*) which differs from the Schwartz distributional derivative in the pHS regularization. Hence we define
where the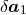 ’s denote the extra terms following from the EHR prescriptions. The pHS-regularized
acceleration (188*) constitutes essentially the result of the first stage of the calculation of
’s denote the extra terms following from the EHR prescriptions. The pHS-regularized
acceleration (188*) constitutes essentially the result of the first stage of the calculation of 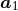 , as reported
in Ref. [193].
, as reported
in Ref. [193].
The next step consists of evaluating the Laurent expansion, in powers of 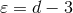 , of the difference
between the dimensional regularization and the pHS (3-dimensional) computation. As we reviewed above,
this difference makes a contribution only when a term generates a pole
, of the difference
between the dimensional regularization and the pHS (3-dimensional) computation. As we reviewed above,
this difference makes a contribution only when a term generates a pole 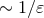 , in which case the
dimensional regularization adds an extra contribution, made of the pole and the finite part associated
with the pole [we consistently neglect all terms
, in which case the
dimensional regularization adds an extra contribution, made of the pole and the finite part associated
with the pole [we consistently neglect all terms 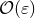 ]. One must then be especially wary of
combinations of terms whose pole parts finally cancel but whose dimensionally regularized finite parts
generally do not, and must be evaluated with care. We denote the above defined difference by
]. One must then be especially wary of
combinations of terms whose pole parts finally cancel but whose dimensionally regularized finite parts
generally do not, and must be evaluated with care. We denote the above defined difference by
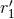 and
and 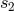 (or
equivalently on
(or
equivalently on 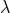 and
and 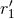 ,
, 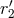 ), and on the parameters associated with dimensional regularization,
namely
), and on the parameters associated with dimensional regularization,
namely  and the characteristic length scale
and the characteristic length scale 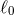 introduced in Eq. (174*). Finally, the result is the
explicit computation of the
introduced in Eq. (174*). Finally, the result is the
explicit computation of the  -expansion of the dimensional regularization (DR) acceleration as
With this result we can prove two theorems [61].
-expansion of the dimensional regularization (DR) acceleration as
With this result we can prove two theorems [61].
Theorem 8. The pole part 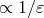 of the DR acceleration (190*) can be re-absorbed (i.e.
renormalized) into some shifts of the two “bare” world-lines:
of the DR acceleration (190*) can be re-absorbed (i.e.
renormalized) into some shifts of the two “bare” world-lines: 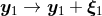 and
and 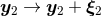 ,
with
,
with 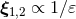 say, so that the result, expressed in terms of the “dressed” quantities, is finite when
say, so that the result, expressed in terms of the “dressed” quantities, is finite when
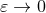 .
.
The situation in harmonic coordinates is to be contrasted with the calculation in ADM-type coordinates within the Hamiltonian formalism, where it was shown that all pole parts directly cancel out in the total 3PN Hamiltonian: No renormalization of the world-lines is needed [163]. The central result is then:
Theorem 9. The renormalized (finite) DR acceleration is physically equivalent to the Hadamard-regularized (HR) acceleration (end result of Ref. [71*]), in the sense that
where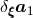 denotes the effect of the shifts on the acceleration, if and only if the HR ambiguity
parameter
denotes the effect of the shifts on the acceleration, if and only if the HR ambiguity
parameter 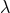 entering the harmonic-coordinates equations of motion takes the unique value (172*).
entering the harmonic-coordinates equations of motion takes the unique value (172*).
The precise shifts 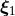 and
and 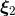 needed in Theorem 9 involve not only a pole contribution
needed in Theorem 9 involve not only a pole contribution
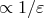 , but also a finite contribution when
, but also a finite contribution when 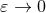 . Their explicit expressions
read:48
. Their explicit expressions
read:48
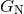 is Newton’s constant,
is Newton’s constant, 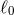 is the characteristic length scale of dimensional regularization,
cf. Eq. (174*), where
is the characteristic length scale of dimensional regularization,
cf. Eq. (174*), where 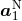 is the Newtonian acceleration of the particle 1 in
is the Newtonian acceleration of the particle 1 in 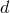 dimensions, and
dimensions, and
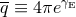 depends on Euler’s constant
depends on Euler’s constant 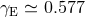 .
.
6.4 Dimensional regularization of the radiation field
We now address the similar problem concerning the binary’s radiation field – to 3PN order
beyond Einstein’s quadrupole formalism (2*) – (3*). As reviewed in Section 6.2, three ambiguity
parameters: 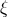 ,
,  and
and 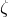 , have been shown to appear in the 3PN expression of the quadrupole
moment [81*, 80*].
, have been shown to appear in the 3PN expression of the quadrupole
moment [81*, 80*].
To apply dimensional regularization, we must use as in Section 6.3 the 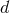 -dimensional
post-Newtonian iteration leading to potentials such as those in Eqs. (177); and we have to
generalize to
-dimensional
post-Newtonian iteration leading to potentials such as those in Eqs. (177); and we have to
generalize to 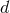 dimensions some key results of the wave generation formalism of Part A.
Essentially, we need the
dimensions some key results of the wave generation formalism of Part A.
Essentially, we need the 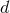 -dimensional analogues of the multipole moments of an isolated source
-dimensional analogues of the multipole moments of an isolated source
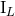 and
and 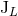 in Eqs. (123). Here we report the result we find in the case of the mass-type
moment:
in Eqs. (123). Here we report the result we find in the case of the mass-type
moment:
in which we denote, generalizing Eqs. (124),
and where for any source densities the underscript ![[ℓ]](article1579x.gif) means the infinite series
means the infinite series
The latter definition represents the 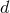 -dimensional version of the post-Newtonian expansion series (126*).
At Newtonian order, the expression (193) reduces to the standard result
-dimensional version of the post-Newtonian expansion series (126*).
At Newtonian order, the expression (193) reduces to the standard result 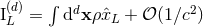 with
with
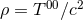 denoting the usual Newtonian density.
denoting the usual Newtonian density.
The ambiguity parameters 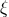 ,
,  and
and 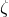 come from the Hadamard regularization of the mass
quadrupole moment
come from the Hadamard regularization of the mass
quadrupole moment 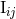 at the 3PN order. The terms corresponding to these ambiguities were found to be
at the 3PN order. The terms corresponding to these ambiguities were found to be
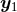 ,
, 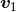 and
and 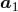 denote the first particle’s position, velocity and acceleration (and the brackets
denote the first particle’s position, velocity and acceleration (and the brackets
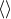 surrounding indices refer to the STF projection). Like in Section 6.3, we express both the Hadamard
and dimensional results in terms of the more basic pHS regularization. The first step of the calculation [80*]
is therefore to relate the Hadamard-regularized quadrupole moment
surrounding indices refer to the STF projection). Like in Section 6.3, we express both the Hadamard
and dimensional results in terms of the more basic pHS regularization. The first step of the calculation [80*]
is therefore to relate the Hadamard-regularized quadrupole moment 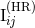 , for general orbits, to its pHS
part:
In the right-hand side we find both the pHS part, and the effect of adding the ambiguities, with some
numerical shifts of the ambiguity parameters (
, for general orbits, to its pHS
part:
In the right-hand side we find both the pHS part, and the effect of adding the ambiguities, with some
numerical shifts of the ambiguity parameters (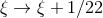 ,
, 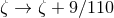 ) due to the difference
between the specific Hadamard-type regularization scheme used in Ref. [81*] and the pHS one. The pHS
part is free of ambiguities but depends on the gauge constants
) due to the difference
between the specific Hadamard-type regularization scheme used in Ref. [81*] and the pHS one. The pHS
part is free of ambiguities but depends on the gauge constants 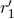 and
and 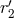 introduced in the
harmonic-coordinates equations of motion [69*, 71*].
introduced in the
harmonic-coordinates equations of motion [69*, 71*].
We next use the 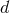 -dimensional moment (193) to compute the difference between the dimensional
regularization (DR) result and the pHS one [62*, 63*]. As in the work on equations of motion, we find that
the ambiguities arise solely from the terms in the integration regions near the particles, that give rise to
poles
-dimensional moment (193) to compute the difference between the dimensional
regularization (DR) result and the pHS one [62*, 63*]. As in the work on equations of motion, we find that
the ambiguities arise solely from the terms in the integration regions near the particles, that give rise to
poles 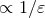 , corresponding to logarithmic ultra-violet (UV) divergences in 3 dimensions. The infra-red
(IR) region at infinity, i.e.,
, corresponding to logarithmic ultra-violet (UV) divergences in 3 dimensions. The infra-red
(IR) region at infinity, i.e., 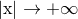 , does not contribute to the difference between
, does not contribute to the difference between  and
and
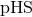 . The compact-support terms in the integrand of Eq. (193), proportional to the matter
source densities
. The compact-support terms in the integrand of Eq. (193), proportional to the matter
source densities 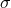 ,
, 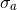 , and
, and 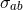 , are also found not to contribute to the difference. We are
therefore left with evaluating the difference linked with the computation of the non-compact terms
in the expansion of the integrand of (193) near the singularities that produce poles in
, are also found not to contribute to the difference. We are
therefore left with evaluating the difference linked with the computation of the non-compact terms
in the expansion of the integrand of (193) near the singularities that produce poles in 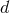 dimensions.
dimensions.
Let 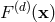 be the non-compact part of the integrand of the quadrupole moment (193) (with
indices
be the non-compact part of the integrand of the quadrupole moment (193) (with
indices 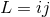 ), where
), where 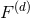 includes the appropriate multipolar factors such as
includes the appropriate multipolar factors such as 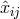 , so that
, so that
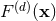 admits a singular expansion of the type (178*). In
practice, the various coefficients
admits a singular expansion of the type (178*). In
practice, the various coefficients 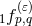 are computed by specializing the general expressions of the
non-linear retarded potentials
are computed by specializing the general expressions of the
non-linear retarded potentials 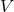 ,
, 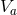 ,
, 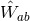 , etc. (valid for general extended sources) to point
particles in
, etc. (valid for general extended sources) to point
particles in 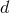 dimensions. On the other hand, the analogue of Eq. (198*) in 3 dimensions is
where
dimensions. On the other hand, the analogue of Eq. (198*) in 3 dimensions is
where 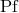 refers to the Hadamard partie finie defined in Eq. (162*). The difference
refers to the Hadamard partie finie defined in Eq. (162*). The difference 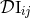 between the DR
evaluation of the
between the DR
evaluation of the 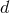 -dimensional integral (198*) and its corresponding three-dimensional evaluation (199*),
reads then
Such difference depends only on the UV behaviour of the integrands, and can therefore be computed
“locally”, i.e., in the vicinity of the particles, when
-dimensional integral (198*) and its corresponding three-dimensional evaluation (199*),
reads then
Such difference depends only on the UV behaviour of the integrands, and can therefore be computed
“locally”, i.e., in the vicinity of the particles, when 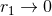 and
and 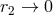 . We find that Eq. (200*)
depends on two constant scales
. We find that Eq. (200*)
depends on two constant scales 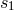 and
and 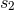 coming from Hadamard’s partie finie (162*), and on
the constants belonging to dimensional regularization, i.e.,
coming from Hadamard’s partie finie (162*), and on
the constants belonging to dimensional regularization, i.e., 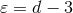 and
and 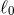 defined by
Eq. (174*). The dimensional regularization of the 3PN quadrupole moment is then obtained
as the sum of the pHS part, and of the difference computed according to Eq. (200*), namely
An important fact, hidden in our too-compact notation (201*), is that the sum of the two terms in the
right-hand side of Eq. (201*) does not depend on the Hadamard regularization scales
defined by
Eq. (174*). The dimensional regularization of the 3PN quadrupole moment is then obtained
as the sum of the pHS part, and of the difference computed according to Eq. (200*), namely
An important fact, hidden in our too-compact notation (201*), is that the sum of the two terms in the
right-hand side of Eq. (201*) does not depend on the Hadamard regularization scales 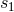 and
and 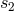 .
Therefore it is possible without changing the sum to re-express these two terms (separately) by means of
the constants
.
Therefore it is possible without changing the sum to re-express these two terms (separately) by means of
the constants 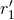 and
and 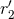 instead of
instead of 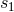 and
and 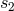 , where
, where 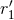 ,
, 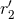 are the two fiducial scales entering
the Hadamard-regularization result (197*). This replacement being made the pHS term in Eq. (201*) is
exactly the same as the one in Eq. (197*). At this stage all elements are in place to prove the following
theorem [62*, 63*].
are the two fiducial scales entering
the Hadamard-regularization result (197*). This replacement being made the pHS term in Eq. (201*) is
exactly the same as the one in Eq. (197*). At this stage all elements are in place to prove the following
theorem [62*, 63*].
Theorem 10. The DR quadrupole moment (201*) is physically equivalent to the Hadamard-regularized one (end result of Refs. [81*, 80*]), in the sense that
where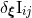 denotes the effect of the same shifts as determined in Theorems 8 and 9, if and only if the HR
ambiguity parameters
denotes the effect of the same shifts as determined in Theorems 8 and 9, if and only if the HR
ambiguity parameters 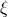 ,
,  and
and 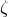 take the unique values reported in Eqs. (173). Moreover, the poles
take the unique values reported in Eqs. (173). Moreover, the poles
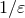 separately present in the two terms in the brackets of Eq. (202*) cancel out, so that the physical
(“dressed”) DR quadrupole moment is finite and given by the limit when
separately present in the two terms in the brackets of Eq. (202*) cancel out, so that the physical
(“dressed”) DR quadrupole moment is finite and given by the limit when 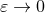 as shown in Eq. (202*).
as shown in Eq. (202*).
This theorem finally provides an unambiguous determination of the 3PN radiation field by dimensional regularization. Furthermore, as reviewed in Section 6.2, several checks of this calculation could be done, which provide independent confirmations for the ambiguity parameters. Such checks also show the powerfulness of dimensional regularization and its validity for describing the classical general-relativistic dynamics of compact bodies.

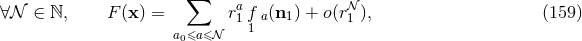


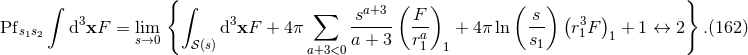
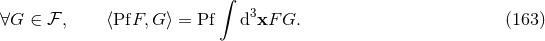
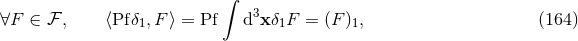
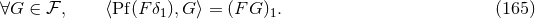
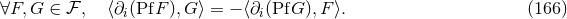
![∂i(PfF ) = Pf(∂iF ) + Di [F ], (167 )](article1301x.gif)
![( [ ] ) i 1- ∑ 1-- Di[F ] = 4 πPf n1 2r1f1 −1 + rk1 f1 − 2− k δ1 + 1 ↔ 2, (168 ) k≥0](article1304x.gif)
![∑ℓ D [F] = ∂ D [∂ F ]. (169 ) L i1...ik−1 ik ik+1...iℓ k=1](article1315x.gif)





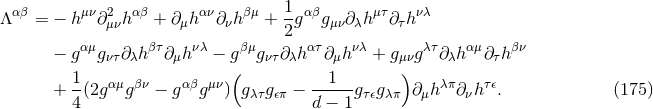
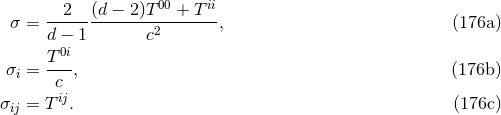
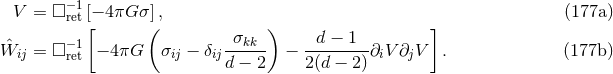
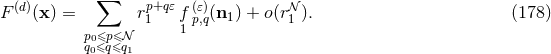

![&tidle; ∫ d P (d)(x′) = Δ −1[F (d)(x)] ≡ − -k- ----d-x----F (d)(x), (180 ) 4π |x − x′|d− 2](article1457x.gif)

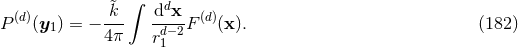
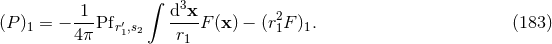

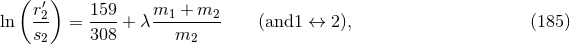
![4 2 Δa [λ] = − 44λ-G-Nm1m--2(m1-+-m2-)n , (186 ) 1 3 r512c6 12](article1516x.gif)
![(HR) (EHR) a 1 = a1 + Δa1 [λ], (187 )](article1520x.gif)



![[ ] a (HR )= lim a (DR )+ δξa1 , (191 ) 1 𝜀→0 1](article1555x.gif)
![[ ( ) ] 11 G2Nm21 1 r′1q1∕2 327 N ξ1 = ------6-- --− 2 ln ------ − ----- a 1 (together with 1 ↔ 2), (192 ) 3 c 𝜀 ℓ0 1540](article1562x.gif)
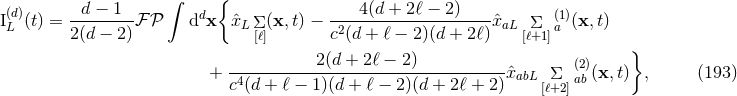
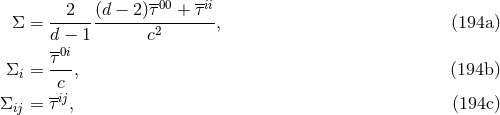
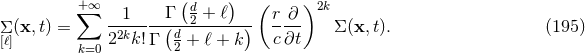
![[( ) ] 44G2Nm31 m1-+--m2- ⟨ij⟩ ⟨ij⟩ ΔIij[ξ,κ, ζ] = 3 c6 ξ + κ m1 y1 a1 + ζv1 v1 + 1 ↔ 2, (196 )](article1588x.gif)
![[ ] (HR) (pHS ) 1 9 Iij = Iij + ΔIij ξ + 22,κ, ζ + 110- . (197 )](article1594x.gif)




![[ ] I(HijR )= lim I(iDjR)+ δξIij , (202 ) 𝜀→0](article1639x.gif)