Part B
Compact Binary Systems
The problem of the motion and gravitational radiation of compact objects in post-Newtonian
approximations is of crucial importance, for at least three reasons listed in the Introduction of this article:
Motion of N planets in the solar system; gravitational radiation reaction force in binary pulsars; direct
detection of gravitational waves from inspiralling compact binaries. As discussed in Section 1.3, the
appropriate theoretical description of inspiralling compact binaries is by two structureless point-particles,
characterized solely by their masses 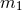 and
and 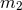 (and possibly their spins), and moving on a
quasi-circular orbit.
(and possibly their spins), and moving on a
quasi-circular orbit.
Strategies to detect and analyze the very weak signals from compact binary inspiral involve matched filtering of a set of accurate theoretical template waveforms against the output of the detectors. Many analyses [139*, 137*, 198, 138*, 393*, 346*, 350*, 284*, 157*, 158*, 159*, 156*, 105*, 106*, 3*, 18*, 111*] have shown that, in order to get sufficiently accurate theoretical templates, one must include post-Newtonian effects up to the 3PN level or higher. Recall that in practice, the post-Newtonian templates for the inspiral phase have to be matched to numerical-relativity results for the subsequent merger and ringdown phases. The match proceeds essentially through two routes: Either the so-called Hybrid templates obtained by direct matching between the PN expanded waveform and the numerical computations [4, 371], or the Effective-One-Body (EOB) templates [108, 109, 161*, 168] that build on post-Newtonian results and extend their realm of validity to facilitate the analytical comparison with numerical relativity [112, 329]. Note also that various post-Newtonian resummation techniques, based on Padé approximants, have been proposed to improve the efficiency of PN templates [157, 158, 161].
6.1 Hadamard self-field regularization
6.2 Hadamard regularization ambiguities
6.3 Dimensional regularization of the equations of motion
6.4 Dimensional regularization of the radiation field
7 Newtonian-like Equations of Motion
7.1 The 3PN acceleration and energy for particles
7.2 Lagrangian and Hamiltonian formulations
7.3 Equations of motion in the center-of-mass frame
7.4 Equations of motion and energy for quasi-circular orbits
7.5 The 2.5PN metric in the near zone
8 Conservative Dynamics of Compact Binaries
8.1 Concept of innermost circular orbit
8.2 Dynamical stability of circular orbits
8.3 The first law of binary point-particle mechanics
8.4 Post-Newtonian approximation versus gravitational self-force
9 Gravitational Waves from Compact Binaries
9.1 The binary’s multipole moments
9.2 Gravitational wave energy flux
9.3 Orbital phase evolution
9.4 Polarization waveforms for data analysis
9.5 Spherical harmonic modes for numerical relativity
10 Eccentric Compact Binaries
10.1 Doubly periodic structure of the motion of eccentric binaries
10.2 Quasi-Keplerian representation of the motion
10.3 Averaged energy and angular momentum fluxes
11 Spinning Compact Binaries
11.1 Lagrangian formalism for spinning point particles
11.2 Equations of motion and precession for spin-orbit effects
11.3 Spin-orbit effects in the gravitational wave flux and orbital phase
Acknowledgments
References