List of Figures
 |
Figure 1:
The binding energy 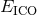 versus versus  in the equal-mass case ( in the equal-mass case (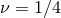 ). Left panel:
Comparison with the numerical relativity result of Gourgoulhon, Grandclément et al. [228, 232]
valid in the corotating case (marked by a star). Points indicated by ). Left panel:
Comparison with the numerical relativity result of Gourgoulhon, Grandclément et al. [228, 232]
valid in the corotating case (marked by a star). Points indicated by 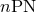 are computed from the
minimum of Eq. (232), and correspond to irrotational binaries. Points denoted by are computed from the
minimum of Eq. (232), and correspond to irrotational binaries. Points denoted by 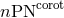 come
from the minimum of the sum of Eqs. (232) and (250*), and describe corotational binaries. Note
the very good convergence of the standard (Taylor-expanded) PN series. Right panel: Numerical
relativity results of Cook, Pfeiffer et al. [133, 121] for quasi-equilibrium (QE) configurations and
various boundary conditions for the lapse function, in the non-spinning (NS), leading-order non
spinning (LN) and corotating (CO) cases. The point from [228, 232] (HKV-GGB) is also reported
as in the left panel, together with IVP, the initial value approach with effective potential [132, 342],
as well as standard PN predictions from the left panel and non-standard (EOB) ones. The agreement
between the QE computation and the standard non-resummed 3PN point is excellent especially in
the irrotational NS case. come
from the minimum of the sum of Eqs. (232) and (250*), and describe corotational binaries. Note
the very good convergence of the standard (Taylor-expanded) PN series. Right panel: Numerical
relativity results of Cook, Pfeiffer et al. [133, 121] for quasi-equilibrium (QE) configurations and
various boundary conditions for the lapse function, in the non-spinning (NS), leading-order non
spinning (LN) and corotating (CO) cases. The point from [228, 232] (HKV-GGB) is also reported
as in the left panel, together with IVP, the initial value approach with effective potential [132, 342],
as well as standard PN predictions from the left panel and non-standard (EOB) ones. The agreement
between the QE computation and the standard non-resummed 3PN point is excellent especially in
the irrotational NS case. |
 |
Figure 2:
Different analytical approximation schemes and numerical techniques to study black hole binaries, depending on the mass ratio 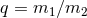 and the post-Newtonian parameter and the post-Newtonian parameter
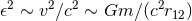 . Post-Newtonian theory and perturbative self-force analysis can be
compared in the post-Newtonian regime ( . Post-Newtonian theory and perturbative self-force analysis can be
compared in the post-Newtonian regime (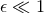 thus thus 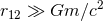 ) of an extreme mass ratio
( ) of an extreme mass ratio
(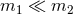 ) binary. ) binary. |
 |
Figure 3:
Variation of the enhancement factor 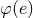 with the eccentricity with the eccentricity  . This function agrees
with the numerical calculation of Ref. [87] modulo a trivial rescaling with the Peters–Mathews
function (356a). The inset graph is a zoom of the function at a smaller scale. The dots represent the
numerical computation and the solid line is a fit to the numerical points. In the circular orbit limit
we have . This function agrees
with the numerical calculation of Ref. [87] modulo a trivial rescaling with the Peters–Mathews
function (356a). The inset graph is a zoom of the function at a smaller scale. The dots represent the
numerical computation and the solid line is a fit to the numerical points. In the circular orbit limit
we have  . . |
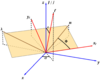 |
Figure 4:
Geometric definitions for the precessional motion of spinning compact binaries [54, 306]. We show (i) the source frame defined by the fixed orthonormal basis 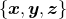 ; (ii) the instantaneous
orbital plane which is described by the orthonormal basis ; (ii) the instantaneous
orbital plane which is described by the orthonormal basis 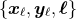 ; (iii) the moving triad ; (iii) the moving triad
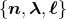 and the associated three Euler angles and the associated three Euler angles 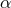 , ,  and and 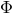 ; (v) the direction of the total
angular momentum ; (v) the direction of the total
angular momentum  which coincides with the which coincides with the  –direction. Dashed lines show projections into
the –direction. Dashed lines show projections into
the  – – plane. plane. |
