References
| * | 1 | Abbott, B. P. et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Observation of
Gravitational Waves from a Binary Black Hole Merger”, Phys. Rev. Lett., 116, 061102 (2016).
[ DOI], [ADS], [arXiv:1602.03837 [gr-qc]].
|
| * | 2 | Abramowicz, M. A. and Kluźniak, W., “A precise determination of black hole spin in GRO
J1655-40”, Astron. Astrophys., 374, L19–L20 (2001). [DOI], [ADS], [astro-ph/0105077].
|
| * | 3 | Ajith, P., Iyer, B. R., Robinson, C. A. K. and Sathyaprakash, B. S., “New class of
post-Newtonian approximants to the waveform templates of inspiralling compact binaries: Test
mass in the Schwarzschild spacetime”, Phys. Rev. D, 71, 044029 (2005). [gr-qc/0412033].
|
| * | 4 | Ajith, P. et al., “Template bank for gravitational waveforms from coalescing binary black holes:
Nonspinning binaries”, Phys. Rev. D, 77, 104017 (2008). [DOI], [ADS], [arXiv:0710.2335 [gr-qc]].
Erratum: Phys. Rev. D, 79, 129901(E) (2009).
|
| * | 5 | Alvi, K., “Energy and angular momentum flow into a black hole in a binary”, Phys. Rev. D,
64, 104020 (2001). [DOI], [arXiv:0107080 [gr-qc]].
|
| * | 6 | Anderson, J. L. and DeCanio, T. C., “Equations of hydrodynamics in general relativity in the
slow motion approximation”, Gen. Relativ. Gravit., 6, 197–237 (1975). [DOI].
|
| * | 7 | Anderson, J. L., Kates, R. E., Kegeles, L. S. and Madonna, R. G., “Divergent integrals of
post-Newtonian gravity: Nonanalytic terms in the near-zone expansion of a gravitationally
radiating system found by matching”, Phys. Rev. D, 25, 2038–2048 (1982). [DOI], [ADS].
|
| * | 8 | Apostolatos, T. A., Cutler, C., Sussman, G. J. and Thorne, K. S., “Spin induced orbital
precession and its modulation of the gravitational wave forms from merging binaries”, Phys.
Rev. D, 49, 6274–6297 (1994). [DOI].
|
| * | 9 | Arun, K. G., Blanchet, L., Iyer, B. R. and Qusailah, M. S., “Inspiralling compact binaries in
quasi-elliptical orbits: The complete 3PN energy flux”, Phys. Rev. D, 77, 064035 (2008). [DOI],
[arXiv:0711.0302].
|
| * | 10 | Arun, K. G., Blanchet, L., Iyer, B. R. and Qusailah, M. S., “Tail effects in the 3PN
gravitational wave energy flux of compact binaries in quasi-elliptical orbits”, Phys. Rev. D, 77,
064034 (2008). [DOI], [arXiv:0711.0250].
|
| * | 11 | Arun, K. G., Blanchet, L., Iyer, B. R. and Qusailah, M. S. S., “The 2.5PN gravitational wave
polarizations from inspiralling compact binaries in circular orbits”, Class. Quantum Grav., 21,
3771–3801 (2004). [DOI], [gr-qc/0404185]. Erratum: Class. Quantum Grav., 22, 3115 (2005).
|
| * | 12 | Arun, K. G., Blanchet, L., Iyer, B. R. and Sinha, S., “Third post-Newtonian angular
momentum flux and the secular evolution of orbital elements for inspiralling compact binaries
in quasi-elliptical orbits”, Phys. Rev. D, 80, 124018 (2009). [DOI], [arXiv:0908.3854].
|
| * | 13 | Arun, K. G., Buonanno, A., Faye, G. and Ochsner, E., “Higher-order spin effects in
the amplitude and phase of gravitational waveforms emitted by inspiraling compact
binaries: Ready-to-use gravitational waveforms”, Phys. Rev. D, 79, 104023 (2009). [DOI],
[arXiv:0810.5336].
|
| * | 14 | Arun, K. G., Iyer, B. R., Qusailah, M. S. S. and Sathyaprakash, B. S., “Probing the non-linear
structure of general relativity with black hole binaries”, Phys. Rev. D, 74, 024006 (2006). [DOI],
[gr-qc/0604067].
|
| * | 15 | Arun, K. G., Iyer, B. R., Qusailah, M. S. S. and Sathyaprakash, B. S., “Testing
post-Newtonian theory with gravitational wave observations”, Class. Quantum Grav., 23,
L37–L43 (2006). [DOI], [ADS], [arXiv:gr-qc/0604018].
|
| * | 16 | Arun, K. G., Iyer, B. R., Sathyaprakash, B. S. and Sinha, S., “Higher harmonics increase
LISA’s mass reach for supermassive black holes”, Phys. Rev. D, 75, 124002 (2007). [DOI],
[arXiv:0704.1086].
|
| * | 17 | Arun, K. G., Iyer, B. R., Sathyaprakash, B. S., Sinha, S. and Van Den Broeck, C., “Higher
signal harmonics, LISA’s angular resolution, and dark energy”, Phys. Rev. D, 76, 104016 (2007).
[DOI], [ADS], [arXiv:0707.3920].
|
| * | 18 | Arun, K. G., Iyer, B. R., Sathyaprakash, B. S. and Sundararajan, P. A., “Parameter
estimation of inspiralling compact binaries using 3.5 post-Newtonian gravitational wave
phasing: The nonspinning case”, Phys. Rev. D, 71, 084008 (2005). [DOI], [gr-qc/0411146].
|
| * | 19 | Bailey, I. and Israel, W., “Lagrangian dynamics of spinning particles and polarized media in
general relativity”, Commun. Math. Phys., 42, 65 (1975). [DOI].
|
| * | 20 | Baker, J. G., Centrella, J., Choi, D.-I., Koppitz, M., van Meter, J. and Miller, M. C., “Getting a
kick out of numerical relativity”, Astrophys. J., 653, L93–L96 (2006). [DOI], [astro-ph/0603204].
|
| * | 21 | Baker, J. G., Centrella, J., Choi, D.-I., Koppitz, M. and van Meter, J. R., “Gravitational-Wave
Extraction from an Inspiraling Configuration of Merging Black Holes”, Phys. Rev. Lett., 96,
111102 (2006). [DOI], [ADS], [arXiv:gr-qc/0511103].
|
| * | 22 | Barack, L., “Gravitational self-force in extreme mass-ratio inspirals”, Class. Quantum Grav.,
26, 213001 (2009). [DOI], [ADS], [arXiv:0908.1664 [gr-qc]].
|
| * | 23 | Barack, L., “Computational Methods for the Self-Force in Black Hole Spacetimes”, in Blanchet,
L., Spallicci, A. and Whiting, B., eds., Mass and Motion in General Relativity, Lectures from
the CNRS School on Mass held in Orléans, France, 23 – 25 June 2008, Fundamental Theories
of Physics, 162, pp. 327–366, (Springer, Dordrecht; New York, 2011). [DOI], [ADS].
|
| * | 24 | Barack, L. and Sago, N., “Gravitational self-force correction to the innermost stable
circular orbit of a Schwarzschild black hole”, Phys. Rev. Lett., 102, 191101 (2009). [DOI],
[arXiv:0902.0573].
|
| * | 25 | Barausse, E., Racine, E. and Buonanno, A., “Hamiltonian of a spinning test particle in curved
spacetime”, Phys. Rev. D, 80, 104025 (2009). [DOI], [arXiv:0907.4745 [gr-qc]].
|
| * | 26 | Bardeen, J. M., Carter, B. and Hawking, S. W., “The Four Laws of Black Hole Mechanics”,
Commun. Math. Phys., 31, 161–170 (1973). [DOI], [ADS].
|
| * | 27 | Barker, B. M. and O’Connell, R. F., “Gravitational two-body problem with arbitrary masses,
spins, and quadrupole moments”, Phys. Rev. D, 12, 329–335 (1975). [DOI].
|
| * | 28 | Barker, B. M. and O’Connell, R. F., “The Gravitational Interaction: Spin, Rotation, and
Quantum Effects – A Review”, Gen. Relativ. Gravit., 11, 149–175 (1979). [DOI].
|
| * | 29 | Baumgarte, T. W., “Innermost stable circular orbit of binary black holes”, Phys. Rev. D, 62,
024018 (2000). [DOI], [ADS].
|
| * | 30 | Bekenstein, J. D., “Gravitational Radiation Recoil and Runaway Black Holes”, Astrophys. J.,
183, 657–664 (1973). [DOI], [ADS].
|
| * | 31 | Bel, L., Damour, T., Deruelle, N., Ibáñez, J. and Martin, J., “Poincaré-Invariant
Gravitational Field and Equations of Motion of two Pointlike Objects: The Postlinear
Approximation of General Relativity”, Gen. Relativ. Gravit., 13, 963–1004 (1981). [DOI].
|
| * | 32 | Benacquista, M. J. and Downing, J. M. B., “Relativistic Binaries in Globular Clusters”, Living
Rev. Relativity, 16, lrr-2013-4 (2013). [DOI], [ADS], [arXiv:1110.4423]. URL (accessed 6 October
2013): http://www.livingreviews.org/lrr-2013-4. |
| * | 33 | Bernard, L., Blanchet, L., Bohé, A., Faye, G. and Marsat, S., “Fokker action of non-spinning
compact binaries at the fourth post-Newtonian approximation”, arXiv, e-print, (2015).
[arXiv:1512.02876 [gr-qc]].
|
| * | 34 | Berti, E., Cardoso, V., Gonzalez, J. A., Sperhake, U., Hannam, M., Husa, S. and Brügmann,
B., “Inspiral, merger, and ringdown of unequal mass black hole binaries: A multipolar analysis”,
Phys. Rev. D, 76, 064034 (2007). [DOI], [ADS], [arXiv:gr-qc/0703053].
|
| * | 35 | Bertotti, B. and Plebański, J. F., “Theory of gravitational perturbations in the fast motion
approximation”, Ann. Phys. (N.Y.), 11, 169–200 (1960). [DOI].
|
| * | 36 | Bini, D. and Damour, T., “Analytical determination of the two-body gravitational interaction
potential at the fourth post-Newtonian approximation”, Phys. Rev. D, 87, 121501 (2013).
[DOI], [ADS], [arXiv:1305.4884 [gr-qc]].
|
| * | 37 | Bini, D. and Damour, T., “Analytic determination of the eight-and-a-half post-Newtonian
self-force contributions to the two-body gravitational interaction potential”, Phys. Rev. D, 89,
104047 (2014). [DOI], [arXiv:1403.2366 [gr-qc]].
|
| * | 38 | Bini, D. and Damour, T., “High-order post-Newtonian contributions to the two-body
gravitational interaction potential from analytical gravitational self-force calculations”, Phys.
Rev. D, 89, 064063 (2014). [DOI], [arXiv:1312.2503 [gr-qc]].
|
| * | 39 | Bini, D., Damour, T. and Geralico, A., “Confirming and improving post-Newtonian and
effective-one-body results from self-force computations along eccentric orbits around a
Schwarzschild black hole”, arXiv, e-print, (2015). [arXiv:1511.04533 [gr-qc]].
|
| * | 40 | Blaes, O., Lee, M. H. and Socrates, A., “The Kozai Mechanism and the Evolution of
Binary Supermassive Black Holes”, Astrophys. J., 578, 775–786 (2002). [DOI], [ADS],
[astro-ph/0203370].
|
| * | 41 | Blanchet, L., “Radiative gravitational fields in general-relativity. II. Asymptotic-behaviour at
future null infinity”, Proc. R. Soc. London, Ser. A, 409, 383–399 (1987). [DOI].
|
| * | 42 | Blanchet, L., Contribution à l’étude du rayonnement gravitationnel émis par un système isolé, Habil. thesis, (Université Paris VI, Paris, 1990). |
| * | 43 | Blanchet, L., “Time asymmetric structure of gravitational radiation”, Phys. Rev. D, 47,
4392–4420 (1993). [DOI].
|
| * | 44 | Blanchet, L., “Second-post-Newtonian generation of gravitational radiation”, Phys. Rev. D,
51, 2559–2583 (1995). [DOI], [gr-qc/9501030].
|
| * | 45 | Blanchet, L., “Energy losses by gravitational radiation in inspiralling compact binaries to five
halves post-Newtonian order”, Phys. Rev. D, 54, 1417–1438 (1996). [DOI], [gr-qc/9603048].
Erratum: Phys. Rev. D, 71, 129904(E) (2005).
|
| * | 46 | Blanchet, L., “Gravitational radiation from relativistic sources”, in Marck, J.-A. and Lasota,
J.-P., eds., Relativistic Gravitation and Gravitational Radiation, Proceedings of the Les Houches
School of Physics, held in Les Houches, Haute Savoie, 26 September – 6 October, 1995,
Cambridge Contemporary Astrophysics, pp. 33–66, (Cambridge University Press, Cambridge,
1997). [gr-qc/9609049], [Google Books].
|
| * | 47 | Blanchet, L., “Gravitational radiation reaction and balance equations to post-Newtonian
order”, Phys. Rev. D, 55, 714–732 (1997). [DOI], [gr-qc/9609049].
|
| * | 48 | Blanchet, L., “Gravitational-wave tails of tails”, Class. Quantum Grav., 15, 113–141 (1998).
[DOI], [gr-qc/9710038]. Erratum: Class. Quantum Grav., 22, 3381 (2005).
|
| * | 49 | Blanchet, L., “On the multipole expansion of the gravitational field”, Class. Quantum Grav.,
15, 1971–1999 (1998). [DOI], [gr-qc/9801101].
|
| * | 50 | Blanchet, L., “Quadrupole-quadrupole gravitational waves”, Class. Quantum Grav., 15, 89–111
(1998). [DOI], [gr-qc/9710037].
|
| * | 51 | Blanchet, L., “Innermost circular orbit of binary black holes at the third post-Newtonian
approximation”, Phys. Rev. D, 65, 124009 (2002). [DOI], [gr-qc/0112056].
|
| * | 52 | Blanchet, L., “Post-Newtonian theory and the two-body problem”, in Blanchet, L., Spallicci,
A. and Whiting, B., eds., Mass and Motion in General Relativity, Lectures from the CNRS
School on Mass held in Orléans, France, 23 – 25 June 2008, Fundamental Theories of Physics,
pp. 125–166, (Springer, Dordrecht; New York, 2011). [DOI], [ADS], [arXiv:0907.3596 [gr-qc]].
|
| * | 53 | Blanchet, L., Buonanno, A. and Faye, G., “Higher-order spin effects in the dynamics of compact
binaries II. Radiation field”, Phys. Rev. D, 74, 104034 (2006). [DOI], [gr-qc/0605140]. Erratum:
Phys. Rev. D, 75, 049903 (2007).
|
| * | 54 | Blanchet, L., Buonanno, A. and Faye, G., “Tail-induced spin-orbit effect in the gravitational
radiation of compact binaries”, Phys. Rev. D, 84, 064041 (2011). [DOI], [arXiv:1104.5659 [gr-qc]].
|
| * | 55 | Blanchet, L., Buonanno, A. and Le Tiec, A., “First law of mechanics for black hole binaries
with spins”, Phys. Rev. D, 87, 024030 (2013). [DOI], [arXiv:1211.1060 [gr-qc]].
|
| * | 56 | Blanchet, L. and Damour, T., “Multipolar radiation reaction in general relativity”, Phys. Lett.
A, 104, 82–86 (1984). [DOI].
|
| * | 57 | Blanchet, L. and Damour, T., “Radiative gravitational fields in general relativity I. General
structure of the field outside the source”, Philos. Trans. R. Soc. London, Ser. A, 320, 379–430
(1986). [DOI].
|
| * | 58 | Blanchet, L. and Damour, T., “Tail-transported temporal correlations in the dynamics of a
gravitating system”, Phys. Rev. D, 37, 1410–1435 (1988). [DOI].
|
| * | 59 | Blanchet, L. and Damour, T., “Post-Newtonian generation of gravitational waves”, Ann. Inst. Henri Poincare A, 50, 377–408 (1989). |
| * | 60 | Blanchet, L. and Damour, T., “Hereditary effects in gravitational radiation”, Phys. Rev. D,
46, 4304–4319 (1992). [DOI].
|
| * | 61 | Blanchet, L., Damour, T. and Esposito-Farèse, G., “Dimensional regularization of the third
post-Newtonian dynamics of point particles in harmonic coordinates”, Phys. Rev. D, 69, 124007
(2004). [DOI], [gr-qc/0311052].
|
| * | 62 | Blanchet, L., Damour, T., Esposito-Farèse, G. and Iyer, B. R., “Gravitational radiation from
inspiralling compact binaries completed at the third post-Newtonian order”, Phys. Rev. Lett.,
93, 091101 (2004). [DOI], [gr-qc/0406012].
|
| * | 63 | Blanchet, L., Damour, T., Esposito-Farèse, G. and Iyer, B. R., “Dimensional regularization
of the third post-Newtonian gravitational wave generation of two point masses”, Phys. Rev. D,
71, 124004 (2005). [DOI], [ADS], [gr-qc/0503044].
|
| * | 64 | Blanchet, L., Damour, T. and Iyer, B. R., “Gravitational waves from inspiralling compact
binaries: Energy loss and wave form to second post-Newtonian order”, Phys. Rev. D, 51,
5360–5386 (1995). [DOI], [gr-qc/9501029].
|
| * | 65 | Blanchet, L., Damour, T. and Iyer, B. R., “Surface-integral expressions for the multipole
moments of post-Newtonian sources and the boosted Schwarzschild solution”, Class. Quantum
Grav., 22, 155 (2005). [DOI], [gr-qc/0410021].
|
| * | 66 | Blanchet, L., Damour, T., Iyer, B. R., Will, C. M. and
Wiseman, A. G., “Gravitational-Radiation Damping of Compact Binary Systems to Second
Post-Newtonian Order”, Phys. Rev. Lett., 74, 3515–3518 (1995). [DOI], [gr-qc/9501027].
|
| * | 67 | Blanchet, L., Detweiler, S., Le Tiec, A. and Whiting, B. F., “Higher-order Post-Newtonian fit
of the gravitational self-force for circular orbits in the Schwarzschild geometry”, Phys. Rev. D,
81, 084033 (2010). [DOI], [ADS], [arXiv:1002.0726 [gr-qc]].
|
| * | 68 | Blanchet, L., Detweiler, S., Le Tiec, A. and Whiting, B. F., “Post-Newtonian and numerical
calculations of the gravitational self-force for circular orbits in the Schwarzschild geometry”,
Phys. Rev. D, 81, 064004 (2010). [DOI], [ADS], [arXiv:0910.0207 [gr-qc]].
|
| * | 69 | Blanchet, L. and Faye, G., “Equations of motion of point-particle binaries at the third
post-Newtonian order”, Phys. Lett. A, 271, 58–64 (2000). [DOI], [gr-qc/0004009].
|
| * | 70 | Blanchet, L. and Faye, G., “Hadamard regularization”, J. Math. Phys., 41, 7675–7714 (2000).
[DOI], [gr-qc/0004008].
|
| * | 71 | Blanchet, L. and Faye, G., “General relativistic dynamics of compact binaries at the third
post-Newtonian order”, Phys. Rev. D, 63, 062005 (2001). [DOI], [gr-qc/0007051].
|
| * | 72 | Blanchet, L. and Faye, G., “Lorentzian regularization and the problem of point-like particles
in general relativity”, J. Math. Phys., 42, 4391–4418 (2001). [DOI], [gr-qc/0006100].
|
| * | 73 | Blanchet, L., Faye, G., Iyer, B. R. and Joguet, B., “Gravitational-wave inspiral of compact
binary systems to 7/2 post-Newtonian order”, Phys. Rev. D, 65, 061501(R) (2002). [DOI],
[gr-qc/0105099]. Erratum: Phys. Rev. D, 71, 129902(E) (2005).
|
| * | 74 | Blanchet, L., Faye, G., Iyer, B. R. and Sinha, S., “The third post-Newtonian gravitational
wave polarisations and associated spherical harmonic modes for inspiralling compact binaries
in quasi-circular orbits”, Class. Quantum Grav., 25, 165003 (2008). [DOI], [arXiv:0802.1249].
|
| * | 75 | Blanchet, L., Faye, G. and Nissanke, S., “Structure of the post-Newtonian expansion in general
relativity”, Phys. Rev. D, 72, 044024 (2005). [DOI].
|
| * | 76 | Blanchet, L., Faye, G. and Ponsot, B., “Gravitational field and equations of motion of compact
binaries to 5/2 post-Newtonian order”, Phys. Rev. D, 58, 124002 (1998). [DOI], [gr-qc/9804079].
|
| * | 77 | Blanchet, L., Faye, G. and Whiting, B. F., “Half-integral conservative post-Newtonian
approximations in the redshift factor of black hole binaries”, Phys. Rev. D, 89, 064026 (2014).
[DOI], [arXiv:1312.2975 [gr-qc]].
|
| * | 78 | Blanchet, L., Faye, G. and Whiting, B. F., “High-order half-integral conservative
post-Newtonian coefficients in the redshift factor of black hole binaries”, Phys. Rev. D, 90,
044017 (2014). [DOI], [arXiv:1405.5151 [gr-qc]].
|
| * | 79 | Blanchet, L. and Iyer, B. R., “Third post-Newtonian dynamics of compact binaries: Equations
of motion in the center-of-mass frame”, Class. Quantum Grav., 20, 755 (2003). [DOI],
[gr-qc/0209089].
|
| * | 80 | Blanchet, L. and Iyer, B. R., “Hadamard regularization of the third post-Newtonian
gravitational wave generation of two point masses”, Phys. Rev. D, 71, 024004 (2005). [DOI],
[gr-qc/0409094].
|
| * | 81 | Blanchet, L., Iyer, B. R. and Joguet, B., “Gravitational waves from inspiralling compact
binaries: Energy flux to third post-Newtonian order”, Phys. Rev. D, 65, 064005 (2002).
[gr-qc/0105098]. Erratum: Phys. Rev. D, 71, 129903(E) (2005).
|
| * | 82 | Blanchet, L., Iyer, B. R., Will, C. M. and Wiseman, A. G., “Gravitational wave forms from
inspiralling compact binaries to second-post-Newtonian order”, Class. Quantum Grav., 13,
575–584 (1996). [DOI], [gr-qc/9602024].
|
| * | 83 | Blanchet, L., Qusailah, M. S. and Will, C. M., “Gravitational recoil of inspiraling
black-hole binaries to second post-Newtonian order”, Astrophys. J., 635, 508 (2005). [DOI],
[astro-ph/0507692].
|
| * | 84 | Blanchet, L. and Sathyaprakash, B. S., “Signal analysis of gravitational wave tails”, Class.
Quantum Grav., 11, 2807–2831 (1994). [DOI].
|
| * | 85 | Blanchet, L. and Sathyaprakash, B. S., “Detecting a Tail Effect in Gravitational-Wave
Experiments”, Phys. Rev. Lett., 74, 1067–1070 (1995). [DOI], [ADS].
|
| * | 86 | Blanchet, L. and Schäfer, G., “Higher order gravitational radiation losses in binary systems”,
Mon. Not. R. Astron. Soc., 239, 845–867 (1989). [DOI].
|
| * | 87 | Blanchet, L. and Schäfer, G., “Gravitational wave tails and binary star systems”, Class.
Quantum Grav., 10, 2699–2721 (1993). [DOI].
|
| * | 88 | Bohé, A., Faye, G., Marsat, S. and Porter, E. K., “Quadratic-in-spin effects in the orbital
dynamics and gravitational-wave energy flux of compact binaries at the 3PN order”, Class.
Quantum Grav., 32, 195010 (2015). [DOI], [arXiv:1501.01529 [gr-qc]].
|
| * | 89 | Bohé, A., Marsat, S. and Blanchet, L., “Next-to-next-to-leading order spin-orbit effects in the
gravitational wave flux and orbital phasing of compact binaries”, Class. Quantum Grav., 30,
135009 (2013). [arXiv:1303.7412].
|
| * | 90 | Bohé, A., Marsat, S., Faye, G. and Blanchet, L., “Next-to-next-to-leading order spin-orbit
effects in the near-zone metric and precession equations of compact binary systems”, Class.
Quantum Grav., 30, 075017 (2013). [arXiv:1212.5520].
|
| * | 91 | Bollini, C. G. and Giambiagi, J. J., “Lowest order ‘divergent’ graphs in v-dimensional space”,
Phys. Lett. B, 40, 566–568 (1972). [DOI].
|
| * | 92 | Bonazzola, S., Gourgoulhon, E. and Marck, J.-A., “Numerical models of irrotational binary
neutron stars in general relativity”, Phys. Rev. Lett., 82, 892–895 (1999). [DOI], [ADS],
[arXiv:gr-qc/9810072 [gr-qc]].
|
| * | 93 | Bondi, H., van der Burg, M. G. J. and Metzner, A. W. K., “Gravitational Waves in General
Relativity. VII. Waves from Axi-Symmetric Isolated Systems”, Proc. R. Soc. London, Ser. A,
269, 21–52 (1962). [DOI], [ADS].
|
| * | 94 | Bonnor, W. B., “Spherical gravitational waves”, Philos. Trans. R. Soc. London, Ser. A, 251,
233–271 (1959). [DOI].
|
| * | 95 | Bonnor, W. B. and Rotenberg, M. A., “Transport of momentum by gravitational waves: Linear
approximation”, Proc. R. Soc. London, Ser. A, 265, 109–116 (1961). [DOI].
|
| * | 96 | Bonnor, W. B. and Rotenberg, M. A., “Gravitational waves from isolated sources”, Proc. R.
Soc. London, Ser. A, 289, 247–274 (1966). [DOI].
|
| * | 97 | Boyle, M., Brown, D. A., Kidder, L. E., Mroué, A. H., Pfeiffer, H. P., Scheel, M. A.,
Cook, G. B. and Teukolsky, S. A., “High-accuracy comparison of numerical relativity
simulations with post-Newtonian expansions”, Phys. Rev. D, 76, 124038 (2007). [DOI], [ADS],
[arXiv:0710.0158 [gr-qc]].
|
| * | 98 | Boyle, M., Buonanno, A., Kidder, L. E., Mroué, A. H., Pan, Y., Pfeiffer, H. P. and Scheel,
M. A., “High-accuracy numerical simulation of black-hole binaries: Computation of the
gravitational-wave energy flux and comparisons with post-Newtonian approximants”, Phys.
Rev. D, 78, 104020 (2008). [DOI], [arXiv:0804.4184 [gr-qc]].
|
| * | 99 | Braginsky, V. B. and Thorne, K. S., “Gravitational-wave bursts with memory and
experimental prospects”, Nature, 327, 123–125 (1987). [DOI].
|
| * | 100 | Breitenlohner, P. and Maison, D., “Dimensional renormalization and the action principle”,
Commun. Math. Phys., 52, 11–38 (1977). [DOI].
|
| * | 101 | Brenneman, L. W. and Reynolds, C. S., “Constraining Black Hole Spin via X-Ray
Spectroscopy”, Astrophys. J., 652, 1028–1043 (2006). [DOI], [ADS], [arXiv:astro-ph/0608502].
|
| * | 102 | Brenneman, L. W. et al., “The Spin of the Supermassive Black Hole in NGC 3783”, Astrophys.
J., 736, 103 (2011). [DOI], [arXiv:1104.1172 [astro-ph.HE]].
|
| * | 103 | Breuer, R. and Rudolph, E., “Radiation reaction and energy loss in the post-Newtonian
approximation of general relativity”, Gen. Relativ. Gravit., 13, 777 (1981). [DOI].
|
| * | 104 | Bruhat, Y., “The Cauchy Problem”, in Witten, L., ed., Gravitation: An Introduction to Current Research, pp. 130–168, (Wiley, New York; London, 1962). |
| * | 105 | Buonanno, A., Chen, Y. and Vallisneri, M., “Detection template families for gravitational waves
from the final stages of binary black-holes binaries: Nonspinning case”, Phys. Rev. D, 67,
024016 (2003). [DOI], [gr-qc/0205122].
|
| * | 106 | Buonanno, A., Chen, Y. and Vallisneri, M., “Detection template families for precessing binaries
of spinning compact binaries: Adiabatic limit”, Phys. Rev. D, 67, 104025 (2003). [DOI],
[gr-qc/0211087].
|
| * | 107 | Buonanno, A., Cook, G. B. and Pretorius, F., “Inspiral, merger, and ring-down of equal-mass
black-hole binaries”, Phys. Rev. D, 75, 124018 (2007). [DOI], [ADS], [gr-qc/0610122].
|
| * | 108 | Buonanno, A. and Damour, T., “Effective one-body approach to general relativistic two-body
dynamics”, Phys. Rev. D, 59, 084006 (1999). [DOI], [ADS], [arXiv:gr-qc/9811091].
|
| * | 109 | Buonanno, A. and Damour, T., “Transition from inspiral to plunge in binary black hole
coalescences”, Phys. Rev. D, 62, 064015 (2000). [DOI], [ADS], [arXiv:gr-qc/0001013].
|
| * | 110 | Buonanno, A., Faye, G. and Hinderer, T., “Spin effects on gravitational waves from inspiralling
compact binaries at second post-Newtonian order”, Phys. Rev. D, 87, 044009 (2013). [DOI],
[arXiv:1209.6349].
|
| * | 111 | Buonanno, A., Iyer, B. R., Pan, Y., Ochsner, E. and Sathyaprakash, B. S., “Comparison of
post-Newtonian templates for compact binary inspiral signals in gravitational-wave detectors”,
Phys. Rev. D, 80, 084043 (2009). [DOI], [arXiv:0907.0700 [gr-qc]].
|
| * | 112 | Buonanno, A., Pan, Y., Pfeiffer, H. P., Scheel, M. A., Buchman, L. T. and Kidder, L. E.,
“Effective-one-body waveforms calibrated to numerical relativity simulations: Coalescence
of nonspinning, equal-mass black holes”, Phys. Rev. D, 79, 124028 (2009). [DOI], [ADS],
[arXiv:0902.0790 [gr-qc]].
|
| * | 113 | Burke, W. L., “Gravitational radiation damping of slowly moving systems calculated using
matched asymptotic expansions”, J. Math. Phys., 12, 401–418 (1971). [DOI], [ADS].
|
| * | 114 | Burke, W. L. and Thorne, K. S., “Gravitational Radiation Damping”, in Carmeli, M., Fickler, S. I. and Witten, L., eds., Relativity, Proceedings of the Relativity Conference in the Midwest, held at Cincinnati, Ohio, June 2 – 6, 1969, pp. 209–228, (Plenum Press, New York; London, 1970). |
| * | 115 | Campanelli, M., “Understanding the fate of merging supermassive black holes”, Class. Quantum
Grav., 22, S387 (2005). [DOI], [astro-ph/0411744].
|
| * | 116 | Campanelli, M., Lousto, C. O., Marronetti, P. and Zlochower, Y., “Accurate Evolutions of
Orbiting Black-Hole Binaries without Excision”, Phys. Rev. Lett., 96, 111101 (2006). [DOI],
[ADS], [arXiv:gr-qc/0511048].
|
| * | 117 | Campanelli, M., Lousto, C. O., Zlochower, Y. and Merritt, D., “Large merger recoils and
spin flips from generic black-hole binaries”, Astrophys. J. Lett., 659, L5–L8 (2007). [DOI],
[arXiv:gr-qc/0701164 [gr-qc]].
|
| * | 118 | Campbell, W. B., Macek, J. and Morgan, T. A., “Relativistic time-dependent multipole
analysis for scalar, electromagnetic, and gravitational fields”, Phys. Rev. D, 15, 2156–2164
(1977). [DOI].
|
| * | 119 | Campbell, W. B. and Morgan, T. A., “Debye Potentials For Gravitational Field”, Physica,
53(2), 264 (1971). [DOI].
|
| * | 120 | Carmeli, M., “The equations of motion of slowly moving particles in the general theory of
relativity”, Nuovo Cimento, 37, 842 (1965). [DOI].
|
| * | 121 | Caudill, M., Cook, G. B., Grigsby, J. D. and Pfeiffer, H. P., “Circular orbits and spin in
black-hole initial data”, Phys. Rev. D, 74, 064011 (2006). [DOI], [ADS], [gr-qc/0605053].
|
| * | 122 | Chandrasekhar, S., “The Post-Newtonian Equations of Hydrodynamics in General Relativity”,
Astrophys. J., 142, 1488–1540 (1965). [DOI], [ADS].
|
| * | 123 | Chandrasekhar, S. and Esposito, F. P., “The 2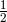 -Post-Newtonian Equations of Hydrodynamics
and Radiation Reaction in General Relativity”, Astrophys. J., 160, 153–179 (1970). [DOI].
|
| * | 124 | Chandrasekhar, S. and Nutku, Y., “The Second Post-Newtonian Equations of Hydrodynamics
in General Relativity”, Astrophys. J., 158, 55–79 (1969). [DOI].
|
| * | 125 | Chatziioannou, K., Poisson, E. and Yunes, N., “Tidal heating and torquing of a Kerr black
hole to next-to-leading order in the tidal coupling”, Phys. Rev. D, 87, 044022 (2013). [DOI],
[ADS], [arXiv:1211.1686 [gr-qc]].
|
| * | 126 | Chicone, C., Kopeikin, S. M., Mashhoon, B. and Retzloff, D. G., “Delay equations and
radiation damping”, Phys. Lett. A, 285, 17–26 (2001). [DOI], [gr-qc/0101122].
|
| * | 127 | Christodoulou, D., “Reversible and irreversible transformations in black-hole physics”, Phys.
Rev. Lett., 25, 1596 (1970). [DOI].
|
| * | 128 | Christodoulou, D., “Nonlinear Nature of Gravitation and Gravitational-Wave Experiments”,
Phys. Rev. Lett., 67, 1486–1489 (1991). [DOI].
|
| * | 129 | Christodoulou, D. and Ruffini, R., “Reversible transformations of a charged black hole”, Phys.
Rev. D, 4, 3552–3555 (1971). [DOI].
|
| * | 130 | Christodoulou, D. and Schmidt, B. G., “Convergent and Asymptotic Iteration Methods in
General Relativity”, Commun. Math. Phys., 68, 275–289 (1979). [DOI].
|
| * | 131 | Collins, J. C., Renormalization: An introduction to renormalization, the renormalization group,
and the operator-product expansion, (Cambridge University Press, Cambridge; New York, 1984).
[Google Books].
|
| * | 132 | Cook, G. B., “Three-dimensional initial data for the collision of two black holes. II.
Quasicircular orbits for equal-mass black holes”, Phys. Rev. D, 50, 5025–5032 (1994). [DOI],
[ADS].
|
| * | 133 | Cook, G. B. and Pfeiffer, H. P., “Excision boundary conditions for black hole initial data”,
Phys. Rev. D, 70, 104016 (2004). [DOI], [ADS].
|
| * | 134 | Cooperstock, F. I. and Booth, D. J., “Angular-Momentum Flux For Gravitational Radiation
to Octupole Order”, Nuovo Cimento B, 62(1), 163–170 (1969). [DOI].
|
| * | 135 | Corinaldesi, E. and Papapetrou, A., “Spinning test-particles in general relativity. II”, Proc. R.
Soc. London, Ser. A, 209, 259–268 (1951). [DOI].
|
| * | 136 | Crowley, R. J. and Thorne, K. S., “Generation of gravitational waves. II. Post-linear formalism
revisited”, Astrophys. J., 215, 624–635 (1977). [DOI].
|
| * | 137 | Cutler, C., Finn, L. S., Poisson, E. and Sussman, G. J., “Gravitational radiation from a particle
in circular orbit around a black hole. II. Numerical results for the nonrotating case”, Phys.
Rev. D, 47, 1511–1518 (1993). [DOI].
|
| * | 138 | Cutler, C. and Flanagan, É. É., “Gravitational waves from merging compact binaries: How
accurately can one extract the binary’s parameters from the inspiral wave form?”, Phys. Rev.
D, 49, 2658–2697 (1994). [DOI], [arXiv:gr-qc/9402014].
|
| * | 139 | Cutler, C. et al., “The Last Three Minutes: Issues in Gravitational-Wave Measurements
of Coalescing Compact Binaries”, Phys. Rev. Lett., 70, 2984–2987 (1993). [DOI],
[astro-ph/9208005].
|
| * | 140 | D’Alembert, J., Traité de Dynamique, (David L’Aine, Paris, 1743). [Google Books].
|
| * | 141 | Damour, T., “Problème des deux corps et freinage de rayonnement en relativité générale”, C. R. Acad. Sci. Ser. II, 294, 1355–1357 (1982). |
| * | 142 | Damour, T., “Gravitational radiation and the motion of compact bodies”, in Deruelle, N. and Piran, T., eds., Rayonnement Gravitationnel / Gravitational Radiation, Proceedings of the Les Houches Summer School, 2 – 21 June 1982, pp. 59–144, (North-Holland, Amsterdam, 1983). |
| * | 143 | Damour, T., “Gravitational radiation reaction in the binary pulsar and the quadrupole formula
controvercy”, Phys. Rev. Lett., 51, 1019–1021 (1983). [DOI].
|
| * | 144 | Damour, T., “An Introduction to the Theory of Gravitational Radiation”, in Carter, B. and Hartle, J. B., eds., Gravitation in Astrophysics: Cargèse 1986, Proceedings of a NATO Advanced Study Institute on Gravitation in Astrophysics, Cargése, France, 15 – 31 July, 1986, NATO ASI Series B, 156, pp. 3–62, (Plenum Press, New York, 1987). |
| * | 145 | Damour, T., “The problem of motion in Newtonian and Einsteinian gravity”, in Hawking,
S. W. and Israel, W., eds., Three Hundred Years of Gravitation, pp. 128–198, (Cambridge
University Press, Cambridge; New York, 1987). [ADS].
|
| * | 146 | Damour, T., “Gravitational self-force in a Schwarzschild background and the effective one-body
formalism”, Phys. Rev. D, 81, 024017 (2010). [DOI], [arXiv:0910.5533 [gr-qc]].
|
| * | 147 | Damour, T. and Deruelle, N., “Lagrangien généralisé du système de deux masses ponctuelles, à l’approximation post-post-newtonienne de la relativité générale”, C. R. Acad. Sci. Ser. II, 293, 537–540 (1981). |
| * | 148 | Damour, T. and Deruelle, N., “Radiation reaction and angular momentum loss in small angle
gravitational scattering”, Phys. Lett. A, 87, 81–84 (1981). [DOI].
|
| * | 149 | Damour, T. and Deruelle, N., “General relativistic celestial mechanics of binary systems I. The
post-Newtonian motion”, Ann. Inst. Henri Poincare A, 43, 107–132 (1985). Online version
(accessed 17 October 2013): http://www.numdam.org/item?id=AIHPA_1985__43_1_107_0.
|
| * | 150 | Damour, T. and Deruelle, N., “General relativistic celestial mechanics of binary systems II. The
post-Newtonian timing formula”, Ann. Inst. Henri Poincare A, 44, 263–292 (1986). Online
version (accessed 17 October 2013): http://www.numdam.org/item?id=AIHPA_1986__44_3_263_0.
|
| * | 151 | Damour, T. and Esposito-Farèse, G., “Testing gravity to second post-Newtonian order: A
field-theory approach”, Phys. Rev. D, 53, 5541–5578 (1996). [DOI], [ADS], [gr-qc/9506063].
|
| * | 152 | Damour, T. and Gopakumar, A., “Gravitational recoil during binary black hole coalescence
using the effective one body approach”, Phys. Rev. D, 73, 124006 (2006). [DOI], [gr-qc/0602117].
|
| * | 153 | Damour, T., Gopakumar, A. and Iyer, B. R., “Phasing of gravitational waves from inspiralling
eccentric binaries”, Phys. Rev. D, 70, 064028 (2004). [DOI], [gr-qc/0404128].
|
| * | 154 | Damour, T. and Iyer, B. R., “Multipole analysis for electromagnetism and linearized gravity
with irreducible Cartesian tensors”, Phys. Rev. D, 43, 3259–3272 (1991). [DOI].
|
| * | 155 | Damour, T. and Iyer, B. R., “Post-Newtonian generation of gravitational waves. II. The spin
moments”, Ann. Inst. Henri Poincare A, 54, 115–164 (1991). Online version (accessed 17
October 2013): http://www.numdam.org/item?id=AIHPA_1991__54_2_115_0.
|
| * | 156 | Damour, T., Iyer, B. R., Jaranowski, P. and Sathyaprakash, B. S., “Gravitational waves from
black hole binary inspiral and merger: The span of third post-Newtonian effective-one-body
templates”, Phys. Rev. D, 67, 064028 (2003). [DOI], [gr-qc/0211041].
|
| * | 157 | Damour, T., Iyer, B. R. and Sathyaprakash, B. S., “Improved filters for gravitational waves
from inspiraling compact binaries”, Phys. Rev. D, 57, 885–907 (1998). [DOI], [gr-qc/9708034].
|
| * | 158 | Damour, T., Iyer, B. R. and Sathyaprakash, B. S., “Frequency-domain P-approximant filters
for time-truncated inspiral gravitational wave signals from compact binaries”, Phys. Rev. D,
62, 084036 (2000). [DOI], [gr-qc/0001023].
|
| * | 159 | Damour, T., Iyer, B. R. and Sathyaprakash, B. S., “Comparison of search templates for
gravitational waves from binary inspiral: 3.5PN update”, Phys. Rev. D, 66, 027502 (2002).
[DOI], [gr-qc/0207021].
|
| * | 160 | Damour, T., Jaranowski, P. and Schäfer, G., “Dynamical invariants for general relativistic
two-body systems at the third post-Newtonian approximation”, Phys. Rev. D, 62, 044024
(2000). [gr-qc/9912092].
|
| * | 161 | Damour, T., Jaranowski, P. and Schäfer, G., “On the determination of the last stable orbit for
circular general relativistic binaries at the third post-Newtonian approximation”, Phys. Rev.
D, 62, 084011 (2000). [ADS], [gr-qc/0005034].
|
| * | 162 | Damour, T., Jaranowski, P. and Schäfer, G., “Poincaré invariance in the ADM Hamiltonian
approach to the general relativistic two-body problem”, Phys. Rev. D, 62, 021501(R) (2000).
[gr-qc/0003051]. Erratum: Phys. Rev. D, 63, 029903(E) (2000).
|
| * | 163 | Damour, T., Jaranowski, P. and Schäfer, G., “Dimensional regularization of the gravitational
interaction of point masses”, Phys. Lett. B, 513, 147–155 (2001). [DOI], [gr-qc/0105038].
|
| * | 164 | Damour, T., Jaranowski, P. and Schäfer, G., “Equivalence between the ADM-Hamiltonian
and the harmonic-coordinates approaches to the third post-Newtonian dynamics of compact
binaries”, Phys. Rev. D, 63, 044021 (2001). [DOI], [gr-qc/0010040]. Erratum: Phys. Rev. D, 66,
029901(E) (2002).
|
| * | 165 | Damour, T., Jaranowski, P. and Schäfer, G., “Hamiltonian of two spinning compact bodies
with next-to-leading order gravitational spin-orbit coupling”, Phys. Rev. D, 77, 064032 (2008).
[DOI], [arXiv:0711.1048].
|
| * | 166 | Damour, T., Jaranowski, P. and Schäfer, G., “Non-local-in-time action for the fourth
post-Newtonian conservative dynamics of two-body systems”, Phys. Rev. D, 89, 064058 (2014).
[DOI], [arXiv:1401.4548 [gr-qc]].
|
| * | 167 | Damour, T., Jaranowski, P. and Schäfer, G., “Fourth post-Newtonian effective one-body
dynamics”, Phys. Rev. D, 91, 084024 (2015). [DOI], [arXiv:1502.07245 [gr-qc]].
|
| * | 168 | Damour, T. and Nagar, A., “The Effective One-Body description of the Two-Body Problem”,
in Blanchet, L., Spallicci, A. and Whiting, B., eds., Mass and Motion in General Relativity,
Lectures from the CNRS School on Mass held in Orléans, France, 23 – 25 June 2008,
Fundamental Theories of Physics, 162, pp. 211–252, (Springer, Dordrecht; New York, 2011).
[DOI], [ADS].
|
| * | 169 | Damour, T. and Schäfer, G., “Lagrangians for n Point Masses at the Second Post-Newtonian
Approximation of General Relativity”, Gen. Relativ. Gravit., 17, 879–905 (1985). [DOI].
|
| * | 170 | Damour, T. and Schäfer, G., “Higher-Order Relativistic Periastron Advances in Binary
Pulsars”, Nuovo Cimento B, 101, 127–176 (1988). [DOI].
|
| * | 171 | Damour, T. and Schmidt, B. G., “Reliability of perturbation theory in general relativity”, J.
Math. Phys., 31, 2441–2458 (1990). [DOI].
|
| * | 172 | Damour, T., Soffel, M. and Xu, C., “General-relativistic celestial mechanics. I. Method and
definition of reference systems”, Phys. Rev. D, 43, 3273–3307 (1991). [DOI], [ADS].
|
| * | 173 | Damour, T. and Taylor, J. H., “On the Orbital Period Change of the Binary Pulsar PSR
1913+16”, Astrophys. J., 366, 501–511 (1991). [DOI], [ADS].
|
| * | 174 | de Andrade, V. C., Blanchet, L. and Faye, G., “Third post-Newtonian dynamics of compact
binaries: Noetherian conserved quantities and equivalence between the harmonic-coordinate
and ADM-Hamiltonian formalisms”, Class. Quantum Grav., 18, 753–778 (2001). [DOI],
[gr-qc/0011063].
|
| * | 175 | Deruelle, N., Sur les équations du mouvement et le rayonnement gravitationnel d’un système binaire en Relativité Générale, Ph.D. thesis, (Université Pierre et Marie Curie, Paris, 1982). |
| * | 176 | Detweiler, S., “Consequence of the gravitational self-force for circular orbits of the Schwarzschild
geometry”, Phys. Rev. D, 77, 124026 (2008). [DOI], [arXiv:0804.3529].
|
| * | 177 | Detweiler, S., “Elementary Development of the Gravitational Self-Force”, in Blanchet, L.,
Spallicci, A. and Whiting, B., eds., Mass and Motion in General Relativity, Lectures from the
CNRS School on Mass held in Orléans, France, 23 – 25 June 2008, Fundamental Theories of
Physics, 162, pp. 271–307, (Springer, Dordrecht; New York, 2011). [DOI], [ADS].
|
| * | 178 | Detweiler, S. and Whiting, B. F., “Self-force via a Green’s function decomposition”, Phys. Rev.
D, 67, 024025 (2003). [DOI], [arXiv:gr-qc/0202086].
|
| * | 179 | Dixon, W. G., “Extended bodies in general relativity: Their description and motion”, in Ehlers, J., ed., Isolated Gravitating Systems in General Relativity (Sistemi gravitazionali isolati in relatività generale), Proceedings of the International School of Physics ‘Enrico Fermi’, Course 67, Varenna on Lake Como, Villa Monastero, Italy, 28 June – 10 July, 1976, pp. 156–219, (North-Holland, Amsterdam; New York, 1979). |
| * | 180 | Eder, E., “Existence, uniqueness and iterative construction of motions of charged particles with
retarded interactions”, Ann. Inst. Henri Poincare A, 39, 1–27 (1983). Online version (accessed
17 October 2013): http://www.numdam.org/item?id=AIHPA_1983__39_1_1_0.
|
| * | 181 | Ehlers, J., “Isolated systems in general relativity”, Ann. N.Y. Acad. Sci., 336, 279–294 (1980).
[DOI].
|
| * | 182 | Ehlers, J., Rosenblum, A., Goldberg, J. N. and Havas, P., “Comments on gravitational
radiation damping and energy loss in binary systems”, Astrophys. J. Lett., 208, L77–L81 (1976).
[DOI], [ADS].
|
| * | 183 | Einstein, A., “Über Gravitationswellen”, Sitzungsber. K. Preuss. Akad. Wiss., 1918, 154–167
(1918). [ADS]. Online version (accessed 31 January 2014): http://echo.mpiwg-berlin.mpg.de/MPIWG:8HSP60BU.
|
| * | 184 | Einstein, A., Infeld, L. and Hoffmann, B., “The Gravitational Equations and the Problem of
Motion”, Ann. Math. (2), 39, 65–100 (1938). [DOI].
|
| * | 185 | Epstein, R. and Wagoner, R. V., “Post-Newtonian Generation of Gravitational Waves”,
Astrophys. J., 197, 717–723 (1975). [DOI], [ADS].
|
| * | 186 | Esposito, L. W. and Harrison, E. R., “Properties of the Hulse-Taylor binary pulsar system”,
Astrophys. J. Lett., 196, L1–L2 (1975). [DOI].
|
| * | 187 | Faber, J. A. and Rasio, F. A., “Binary Neutron Star Mergers”, Living Rev. Relativity, 15,
lrr-2012-8 (2012). [DOI], [ADS], [arXiv:1204.3858 [gr-qc]]. URL (accessed 6 October 2013): http://www.livingreviews.org/lrr-2012-8. |
| * | 188 | Fabian, A. C. and Miniutti, G., “The X-ray spectra of accreting Kerr black holes”, in Wiltshire,
D. L., Visser, M. and Scott, S. M., eds., The Kerr Spacetime: Rotating Black Holes in
General Relativity, 9, (Cambridge University Press, Cambridge; New York, 2009). [ADS],
[arXiv:astro-ph/0507409].
|
| * | 189 | Favata, M., “Post-Newtonian corrections to the gravitational-wave memory for quasicircular,
inspiralling compact binaries”, Phys. Rev. D, 80, 024002 (2009). [DOI], [ADS], [arXiv:0812.0069].
|
| * | 190 | Favata, M., “Conservative corrections to the innermost stable circular orbit (ISCO) of a Kerr
black hole: a new gauge-invariant post-Newtonian ISCO condition, and the ISCO shift due
to test-particle spin and the gravitational self-force”, Phys. Rev. D, 83, 024028 (2011). [DOI],
[arXiv:1010.2553].
|
| * | 191 | Favata, M., “Conservative self-force correction to the innermost stable circular orbit:
comparison with multiple post-Newtonian-based methods”, Phys. Rev. D, 83, 024027 (2011).
[DOI], [arXiv:1008.4622].
|
| * | 192 | Favata, M., “The gravitational-wave memory from eccentric binaries”, Phys. Rev. D, 84, 124013
(2011). [DOI], [arXiv:1108.3121].
|
| * | 193 | Faye, G., Equations du mouvement d’un système binaire d’objets compact à l’approximation post-newtonienne, Ph.D. thesis, (Université Paris VI, Paris, 1999). |
| * | 194 | Faye, G., Blanchet, L. and Buonanno, A., “Higher-order spin effects in the dynamics of compact
binaries I. Equations of motion”, Phys. Rev. D, 74, 104033 (2006). [DOI], [gr-qc/0605139].
|
| * | 195 | Faye, G., Blanchet, L. and Iyer, B. R., “Non-linear multipole interactions and
gravitational-wave octupole modes for inspiralling compact binaries to third-and-a-half
post-Newtonian order”, Class. Quantum Grav., 32, 045016 (2015). [arXiv:1409.3546 [gr-qc]].
|
| * | 196 | Faye, G., Jaranowski, P. and Schäfer, G., “Skeleton approximate solution of the Einstein
field equations for multiple black-hole systems”, Phys. Rev. D, 69, 124029 (2004). [DOI],
[gr-qc/0311018].
|
| * | 197 | Faye, G., Marsat, S., Blanchet, L. and Iyer, B. R., “The third and a half post-Newtonian
gravitational wave quadrupole mode for quasi-circular inspiralling compact binaries”, Class.
Quantum Grav., 29, 175004 (2012). [DOI], [arXiv:1204.1043].
|
| * | 198 | Finn, L. S. and Chernoff, D. F., “Observing binary inspiral in gravitational radiation: One
interferometer”, Phys. Rev. D, 47, 2198–2219 (1993). [DOI], [arXiv:gr-qc/9301003].
|
| * | 199 | Fitchett, M. J., “The influence of gravitational wave momentum losses on the centre of mass
motion of a Newtonian binary system”, Mon. Not. R. Astron. Soc., 203, 1049–1062 (1983).
[ADS].
|
| * | 200 | Flanagan, É.É. and Hinderer, T., “Constraining neutron star tidal Love numbers with
gravitational wave detectors”, Phys. Rev. D, 77, 021502 (2008). [DOI], [ADS], [arXiv:0709.1915
[astro-ph]].
|
| * | 201 | Fock, V. A., “On motion of finite masses in general relativity”, J. Phys. (Moscow), 1(2), 81–116 (1939). |
| * | 202 | Fock, V. A., Theory of space, time and gravitation, (Pergamon, London, 1959). |
| * | 203 | Foffa, S. and Sturani, R., “Effective field theory calculation of conservative binary dynamics at
third post-Newtonian order”, Phys. Rev. D, 84, 044031 (2011). [DOI], [arXiv:1104.1122 [gr-qc]].
|
| * | 204 | Foffa, S. and Sturani, R., “The dynamics of the gravitational two-body problem in the
post-Newtonian approximation at quadratic order in the Newton’s constant”, Phys. Rev. D,
87, 064011 (2012). [arXiv:1206.7087 [gr-qc]].
|
| * | 205 | Foffa, S. and Sturani, R., “Tail terms in gravitational radiation reaction via effective field
theory”, Phys. Rev. D, 87, 044056 (2013). [DOI], [arXiv:1111.5488 [gr-qc]].
|
| * | 206 | Foffa, S. and Sturani, R., “Effective field theory methods to model compact binaries”, Class.
Quantum Grav., 31, 043001 (2014). [DOI], [ADS], [arXiv:1309.3474 [gr-qc]].
|
| * | 207 | Fokker, A. D., “Ein invarianter Variationssatz für die Bewegung mehrerer elektrischer
Massenteilchen”, Z. Phys., 58, 386–393 (1929). [DOI], [ADS].
|
| * | 208 | Friedman, J. L., Uryū, K. and Shibata, M., “Thermodynamics of binary black holes and
neutron stars”, Phys. Rev. D, 65, 064035 (2002). [DOI]. Erratum: Phys. Rev. D, 70, 129904(E)
(2004).
|
| * | 209 | Fujita, R., “Gravitational Radiation for Extreme Mass Ratio Inspirals to the 14th
Post-Newtonian Order”, Prog. Theor. Phys., 127, 583–590 (2012). [DOI], [arXiv:1104.5615
[gr-qc]].
|
| * | 210 | Fujita, R., “Gravitational Waves from a Particle in Circular Orbits around a Schwarzschild
Black Hole to the 22nd Post-Newtonian Order”, Prog. Theor. Phys., 128, 971–992 (2012).
[DOI], [ADS], [arXiv:1211.5535 [gr-qc]].
|
| * | 211 | Futamase, T., “Gravitational radiation reaction in the Newtonian limit”, Phys. Rev. D, 28,
2373–2381 (1983). [DOI].
|
| * | 212 | Futamase, T., “Strong-field point-particle limit and the equations of motion in the binary
pulsar”, Phys. Rev. D, 36, 321–329 (1987). [DOI].
|
| * | 213 | Futamase, T. and Itoh, Y., “The Post-Newtonian Approximation for Relativistic Compact
Binaries”, Living Rev. Relativity, 10, lrr-2007-2 (2007). [DOI], [ADS]. URL (accessed 6 October
2013): http://www.livingreviews.org/lrr-2007-2. |
| * | 214 | Futamase, T. and Schutz, B. F., “Newtonian and post-Newtonian approximations are
asymptotic to general relativity”, Phys. Rev. D, 28, 2363–2372 (1983). [DOI].
|
| * | 215 | Galley, C. R., Leibovich, A. K., Porto, R. A. and Ross, A., “The tail effect in gravitational
radiation-reaction: time non-locality and renormalization group evolution”, arXiv, e-print,
(2015). [arXiv:1511.07379 [gr-qc]].
|
| * | 216 | Gal’tsov, D. V., Matiukhin, A. A. and Petukhov, V. I., “Relativistic corrections to the
gravitational radiation of a binary system and the fine structure of the spectrum”, Phys. Lett.
A, 77, 387–390 (1980). [DOI].
|
| * | 217 | Gergely, L.Á., “Spin-spin effects in radiating compact binaries”, Phys. Rev. D, 61, 024035
(1999). [DOI], [gr-qc/9911082].
|
| * | 218 | Gergely, L.Á., “Second post-Newtonian radiative evolution of the relative orientations of
angular momenta in spinning compact binaries”, Phys. Rev. D, 62, 024007 (2000). [DOI],
[gr-qc/0003037].
|
| * | 219 | Geroch, R., “Multipole Moments. II. Curved Space”, J. Math. Phys., 11, 2580–2588 (1970).
[DOI], [ADS].
|
| * | 220 | Geroch, R. and Horowitz, G. T., “Asymptotically simple does not imply asymptotically Minkowskian”, Phys. Rev. Lett., 40, 203–206 (1978). |
| * | 221 | Goldberger, W. D. and Ross, A., “Gravitational radiative corrections from effective field
theory”, Phys. Rev. D, 81, 124015 (2010). [DOI], [arXiv:0912.4254].
|
| * | 222 | Goldberger, W. D., Ross, A. and Rothstein, I. Z., “Black hole mass dynamics and
renormalization group evolution”, Phys. Rev. D, 89, 124033 (2014). [DOI], [ADS],
[arXiv:1211.6095 [hep-th]].
|
| * | 223 | Goldberger, W. D. and Rothstein, I. Z., “Effective field theory of gravity for extended objects”,
Phys. Rev. D, 73, 104029 (2006). [DOI], [arXiv:hep-th/0409156 [hep-th]].
|
| * | 224 | Gopakumar, A. and Iyer, B. R., “Gravitational waves from inspiraling compact binaries:
Angular momentum flux, evolution of the orbital elements and the waveform to the second
post-Newtonian order”, Phys. Rev. D, 56, 7708–7731 (1997). [DOI], [arXiv:gr-qc/9710075].
|
| * | 225 | Gopakumar, A. and Iyer, B. R., “Second post-Newtonian gravitational wave polarizations
for compact binaries in elliptical orbits”, Phys. Rev. D, 65, 084011 (2002). [DOI],
[arXiv:gr-qc/0110100].
|
| * | 226 | Gopakumar, A., Iyer, B. R. and Iyer, S., “Second post-Newtonian gravitational radiation
reaction for two-body systems: Nonspinning bodies”, Phys. Rev. D, 55, 6030–6053 (1997).
[DOI], [arXiv:gr-qc/9703075].
|
| * | 227 | Gou, L. et al., “The extreme spin of the black hole in Cygnus X-1”, Astrophys. J., 742, 85
(2011). [DOI], [arXiv:1106.3690 [astro-ph.HE]].
|
| * | 228 | Gourgoulhon, E., Grandclément, P. and Bonazzola, S., “Binary black holes in circular orbits.
I. A global spacetime approach”, Phys. Rev. D, 65, 044020 (2002). [DOI], [ADS], [gr-qc/0106015].
|
| * | 229 | Gourgoulhon, E., Grandclément, P., Taniguchi, K., Marck, J.-A. and Bonazzola, S.,
“Quasi-equilibrium sequences of synchronized and irrotational binary neutron stars in general
relativity”, Phys. Rev. D, 63, 064029 (2001). [DOI], [gr-qc/0007028].
|
| * | 230 | Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series and Products, (Academic Press, San Diego; London, 1980). |
| * | 231 | Gralla, S. E. and Wald, R. M., “A rigorous derivation of gravitational self-force”, Class.
Quantum Grav., 25, 205009 (2008). [DOI], [arXiv:0806.3293].
|
| * | 232 | Grandclément, P., Gourgoulhon, E. and Bonazzola, S., “Binary black holes in circular orbits.
II. Numerical methods and first results”, Phys. Rev. D, 65, 044021 (2002). [DOI], [ADS].
|
| * | 233 | Grandclément, P. and Novak, J., “Spectral Methods for Numerical Relativity”, Living Rev.
Relativity, 12, lrr-2009-1 (2009). [DOI], [ADS], [arXiv:0706.2286 [gr-qc]]. URL (accessed 6 October
2013): http://www.livingreviews.org/lrr-2009-1. |
| * | 234 | Grishchuk, L. P. and Kopeikin, S. M., “Equations of motion for isolated bodies with relativistic corrections including the radiation-reaction force”, in Kovalevsky, J. and Brumberg, V. A., eds., Relativity in Celestial Mechanics and Astrometry: High Precision Dynamical Theories and Observational Verifications, Proceedings of the 114th Symposium of the International Astronomical Union, held in Leningrad, USSR, May 28 – 31, 1985, pp. 19–34, (Reidel, Dordrecht; Boston, 1986). |
| * | 235 | Gultekin, K., Miller, M. C. and Hamilton, D. P., “Growth of Intermediate-Mass Black Holes
in Globular Clusters”, Astrophys. J., 616, 221 (2004). [DOI], [astro-ph/0402532].
|
| * | 236 | Hadamard, J., Le problème de Cauchy et les équations aux dérivées partielles linéaires hyperboliques, (Hermann, Paris, 1932). |
| * | 237 | Hannam, M., Husa, S., González, J. A., Sperhake, U. and Brügmann, B., “Where
post-Newtonian and numerical-relativity waveforms meet”, Phys. Rev. D, 77, 044020 (2008).
[DOI], [ADS], [arXiv:0706.1305].
|
| * | 238 | Hansen, R. O., “Multipole moments of stationary space-times”, J. Math. Phys., 15, 46–52
(1974). [DOI], [ADS].
|
| * | 239 | Hanson, A. J. and Regge, T., “The Relativistic Spherical Top”, Ann. Phys. (N.Y.), 87, 498–566
(1974). [DOI].
|
| * | 240 | Hari Dass, N. D. and Soni, V., “Feynman graph derivation of the Einstein quadrupole
formula”, J. Phys. A: Math. Gen., 15, 473–492 (1982). [DOI].
|
| * | 241 | Hartung, J. and Steinhoff, J., “Next-to-leading order spin-orbit and spin(a)-spin(b)
Hamiltonians for n gravitating spinning compact objects”, Phys. Rev. D, 83, 044008 (2011).
[DOI], [arXiv:1011.1179 [gr-qc]].
|
| * | 242 | Hartung, J. and Steinhoff, J., “Next-to-next-to-leading order post-Newtonian spin-orbit
Hamiltonian for self-gravitating binaries”, Ann. Phys. (Berlin), 523, 783–790 (2011). [DOI],
[ADS], [arXiv:1104.3079 [gr-qc]].
|
| * | 243 | Hartung, J. and Steinhoff, J., “Next-to-next-to-leading order post-Newtonian spin(1)-spin(2)
Hamiltonian for self-gravitating binaries”, Ann. Phys. (Berlin), 523, 919–924 (2011). [DOI],
[ADS], [arXiv:1107.4294 [gr-qc]].
|
| * | 244 | Hartung, J., Steinhoff, J. and Schäfer, G., “Next-to-next-to-leading order post-Newtonian
linear-in-spin binary Hamiltonians”, Ann. Phys. (Berlin), 525, 359–394 (2013). [DOI], [ADS],
[arXiv:1302.6723 [gr-qc]].
|
| * | 245 | Hergt, S. and Schäfer, G., “Higher-order-in-spin interaction Hamiltonians for binary black
holes from Poincaré invariance”, Phys. Rev. D, 78, 124004 (2008). [DOI], [arXiv:0809.2208
[gr-qc]].
|
| * | 246 | Hergt, S. and Schäfer, G., “Higher-order-in-spin interaction Hamiltonians for binary black
holes from source terms of Kerr geometry in approximate ADM coordinates”, Phys. Rev. D,
77, 104001 (2008). [DOI], [arXiv:0712.1515 [gr-qc]].
|
| * | 247 | Hergt, S., Steinhoff, J. and Schäfer, G., “The reduced Hamiltonian for next-to-leading-order
spin-squared dynamics of general compact binaries”, Class. Quantum Grav., 27, 135007 (2010).
[DOI], [arXiv:1002.2093 [gr-qc]].
|
| * | 248 | Hopper, S., Kavanagh, C. and Ottewill, A. C., “Analytic self-force calculations in the
post-Newtonian regime: eccentric orbits on a Schwarzschild background”, Phys. Rev. D, 93,
044010 (2016). [DOI], [arXiv:1512.01556 [gr-qc]].
|
| * | 249 | Hotokezaka, K., Kyutoku, K. and Shibata, M., “Exploring tidal effects of coalescing binary
neutron stars in numerical relativity”, Phys. Rev. D, 87, 044001 (2013). [DOI], [arXiv:1301.3555
[gr-qc]].
|
| * | 250 | Hulse, R. A. and Taylor, J. H., “Discovery of a pulsar in a binary system”, Astrophys. J., 195,
L51–L53 (1975). [DOI], [ADS].
|
| * | 251 | Hunter, A. J. and Rotenberg, M. A., “The double-series approximation method in general
relativity. I. Exact solution of the (24) approximation. II. Discussion of ‘wave tails’ in the (2s)
approximation”, J. Phys. A: Math. Gen., 2, 34–49 (1969). [DOI].
|
| * | 252 | Isaacson, R. A. and Winicour, J., “Harmonic and Null Descriptions of Gravitational
Radiation”, Phys. Rev., 168, 1451–1456 (1968). [DOI].
|
| * | 253 | Itoh, Y., “Equation of motion for relativistic compact binaries with the strong field point
particle limit: Third post-Newtonian order”, Phys. Rev. D, 69, 064018 (2004). [DOI].
|
| * | 254 | Itoh, Y., “Third-and-a-half order post-Newtonian equations of motion for relativistic compact
binaries using the strong field point particle limit”, Phys. Rev. D, 80, 124003 (2009). [DOI],
[arXiv:0911.4232 [gr-qc]].
|
| * | 255 | Itoh, Y. and Futamase, T., “New derivation of a third post-Newtonian equation of motion for
relativistic compact binaries without ambiguity”, Phys. Rev. D, 68, 121501(R) (2003). [DOI],
[gr-qc/0310028].
|
| * | 256 | Itoh, Y....., Futamase, T. and Asada, H., “Equation of motion for relativistic compact binaries
with the strong field point particle limit: Formulation, the first post-Newtonian order, and
multipole terms”, Phys. Rev. D, 62, 064002 (2000). [DOI], [gr-qc/9910052].
|
| * | 257 | Itoh, Y., Futamase, T. and Asada, H., “Equation of motion for relativistic compact binaries
with the strong field point particle limit: The second and half post-Newtonian order”, Phys.
Rev. D, 63, 064038 (2001). [DOI], [gr-qc/0101114].
|
| * | 258 | Iyer, B. R. and Will, C. M., “Post-Newtonian gravitational radiation reaction for two-body
systems”, Phys. Rev. Lett., 70, 113–116 (1993). [DOI].
|
| * | 259 | Iyer, B. R. and Will, C. M., “Post-Newtonian gravitational radiation reaction for two-body
systems: Nonspinning bodies”, Phys. Rev. D, 52, 6882–6893 (1995). [DOI].
|
| * | 260 | Jaranowski, P. and Schäfer, G., “Radiative 3.5 post-Newtonian ADM Hamiltonian for
many-body point-mass systems”, Phys. Rev. D, 55, 4712–4722 (1997). [DOI].
|
| * | 261 | Jaranowski, P. and Schäfer, G., “Third post-Newtonian higher order ADM Hamilton dynamics
for two-body point-mass systems”, Phys. Rev. D, 57, 7274–7291 (1998). [DOI], [gr-qc/9712075].
|
| * | 262 | Jaranowski, P. and Schäfer, G., “Binary black-hole problem at the third post-Newtonian
approximation in the orbital motion: Static part”, Phys. Rev. D, 60, 124003 (1999). [DOI],
[gr-qc/9906092].
|
| * | 263 | Jaranowski, P. and Schäfer, G., “The binary black-hole dynamics at the third post-Newtonian
order in the orbital motion”, Ann. Phys. (Berlin), 9, 378–383 (2000). [DOI], [gr-qc/0003054].
|
| * | 264 | Jaranowski, P. and Schäfer, G., “Towards the fourth post-Newtonian Hamiltonian for
two-point-mass systems”, Phys. Rev. D, 86, 061503(R) (2012). [DOI], [arXiv:1207.5448 [gr-qc]].
|
| * | 265 | Jaranowski, P. and Schäfer, G., “Dimensional regularization of local singularities in the 4th
post-Newtonian two-point-mass Hamiltonian”, Phys. Rev. D, 87, 081503(R) (2013). [DOI],
[arXiv:1303.3225 [gr-qc]].
|
| * | 266 | Jaranowski, P. and Schäfer, G., “Derivation of the local-in-time fourth post-Newtonian
ADM Hamiltonian for spinless compact binaries”, Phys. Rev. D, 92, 124043 (2015). [DOI],
[arXiv:1508.01016 [gr-qc]].
|
| * | 267 | Junker, W. and Schäfer, G., “Binary systems: higher order gravitational radiation damping
and wave emission”, Mon. Not. R. Astron. Soc., 254, 146–164 (1992). [ADS].
|
| * | 268 | Kavanagh, C., Ottewill, A. C. and Wardell, B., “Analytical high-order post-Newtonian
expansions for extreme mass ratio binaries”, Phys. Rev. D, 92, 084025 (2015). [DOI], [ADS],
[arXiv:1503.02334 [gr-qc]].
|
| * | 269 | Kerlick, G. D., “Finite reduced hydrodynamic equations in the slow-motion approximation to
general relativity. Part I. First post-Newtonian equations”, Gen. Relativ. Gravit., 12, 467–482
(1980). [DOI].
|
| * | 270 | Kerlick, G. D., “Finite reduced hydrodynamic equations in the slow-motion approximation to
general relativity. Part II. Radiation reaction and higher-order divergent terms”, Gen. Relativ.
Gravit., 12, 521–543 (1980). [DOI].
|
| * | 271 | Kidder, L. E., “Coalescing binary systems of compact objects to (post)5∕2-Newtonian order.
V. Spin effects”, Phys. Rev. D, 52, 821–847 (1995). [DOI], [ADS].
|
| * | 272 | Kidder, L. E., “Using full information when computing modes of post-Newtonian waveforms
from inspiralling compact binaries in circular orbits”, Phys. Rev. D, 77, 044016 (2008). [DOI],
[arXiv:0710.0614].
|
| * | 273 | Kidder, L. E., Blanchet, L. and Iyer, B. R., “A note on the radiation reaction in the 2.5PN
waveform from inspiralling binaries in quasi-circular orbits”, Class. Quantum Grav., 24, 5307
(2007). [DOI], [arXiv:0706.0726].
|
| * | 274 | Kidder, L. E., Will, C. M. and Wiseman, A. G., “Coalescing binary systems of compact
objects to (post)5∕2-Newtonian order. III. Transition from inspiral to plunge”, Phys. Rev. D,
47, 3281–3291 (1993). [DOI], [ADS].
|
| * | 275 | Kidder, L. E., Will, C. M. and Wiseman, A. G., “Spin effects in the inspiral of coalescing
compact binaries”, Phys. Rev. D, 47, R4183–R4187 (1993). [DOI].
|
| * | 276 | Kochanek, C. S., “Coalescing binary neutron stars”, Astrophys. J., 398, 234–247 (1992). [DOI],
[ADS].
|
| * | 277 | Kol, B. and Smolkin, M., “Non-relativistic gravitation: From Newton to Einstein and back”,
Class. Quantum Grav., 25, 145011 (2008). [DOI], [arXiv:0712.4116 [hep-th]].
|
| * | 278 | Königsdörffer, C., Faye, G. and Schäfer, G., “The binary black-hole dynamics at the
third-and-a-half post-Newtonian order in the ADM-formalism”, Phys. Rev. D, 68, 044004
(2003). [DOI], [astro-ph/0305048].
|
| * | 279 | Königsdörffer, C. and Gopakumar, A., “Phasing of gravitational waves from inspiralling
eccentric binaries at the third-and-a-half post-Newtonian order”, Phys. Rev. D, 73, 124012
(2006). [DOI], [ADS], [gr-qc/0603056].
|
| * | 280 | Kopeikin, S. M., “The equations of motion of extended bodies in general-relativity with conservative corrections and radiation damping taken into account”, Astron. Zh., 62, 889–904 (1985). |
| * | 281 | Kopeikin, S. M., “Celestial Coordinate Reference Systems in Curved Spacetime”, Celest.
Mech., 44, 87 (1988). [DOI].
|
| * | 282 | Kopeikin, S. M., Schäfer, G., Gwinn, C. R. and Eubanks, T. M., “Astrometric and timing
effects of gravitational waves from localized sources”, Phys. Rev. D, 59, 084023 (1999). [DOI],
[ADS], [gr-qc/9811003].
|
| * | 283 | Kozai, Y., “Secular perturbations of asteroids with high inclination and eccentricity”, Astron.
J., 67, 591–598 (1962). [DOI], [ADS].
|
| * | 284 | Królak, A., Kokkotas, K. D. and Schäfer, G., “Estimation of the post-Newtonian parameters
in the gravitational-wave emission of a coalescing binary”, Phys. Rev. D, 52, 2089–2111 (1995).
[DOI], [gr-qc/9503013].
|
| * | 285 | Landau, L. D. and Lifshitz, E. M., The classical theory of fields, (Pergamon Press, Oxford; New York, 1971), 3rd edition. |
| * | 286 | Le Tiec, A., “First law of mechanics for compact binaries on eccentric orbits”, Phys. Rev. D,
92, 084021 (2015). [DOI], [arXiv:1506.05648 [gr-qc]].
|
| * | 287 | Le Tiec, A., Barausse, E. and Buonanno, A., “Gravitational Self-Force Correction to the
Binding Energy of Compact Binary Systems”, Phys. Rev. Lett., 108, 131103 (2012). [DOI],
[arXiv:1111.5609 [gr-qc]].
|
| * | 288 | Le Tiec, A. and Blanchet, L., “The Close-Limit Approximation for Black Hole Binaries
with Post-Newtonian Initial Conditions”, Class. Quantum Grav., 27, 045008 (2010). [DOI],
[arXiv:0901.4593 [gr-qc]].
|
| * | 289 | Le Tiec, A., Blanchet, L. and Whiting, B. F., “First law of binary black hole mechanics
in general relativity and post-Newtonian theory”, Phys. Rev. D, 85, 064039 (2012). [DOI],
[arXiv:1111.5378 [gr-qc]].
|
| * | 290 | Le Tiec, A., Blanchet, L. and Will, C. M., “Gravitational-Wave Recoil from the Ringdown
Phase of Coalescing Black Hole Binaries”, Class. Quantum Grav., 27, 012001 (2010). [DOI],
[arXiv:0901.4594 [gr-qc]].
|
| * | 291 | Le Tiec, A., Mroué, A. H., Barack, L., Buonanno, A., Pfeiffer, H. P., Sago, N. and Taracchini,
A., “Periastron Advance in Black-Hole Binaries”, Phys. Rev. Lett., 107, 141101 (2011).
[arXiv:1106.3278 [gr-qc]].
|
| * | 292 | Levi, M., “Next-to-leading order gravitational spin-orbit coupling in an effective field theory
approach”, Phys. Rev. D, 82, 104004 (2010). [DOI], [arXiv:1006.4139 [gr-qc]].
|
| * | 293 | Levi, M., “Next-to-leading order gravitational spin1-spin2 coupling with Kaluza-Klein
reduction”, Phys. Rev. D, 82, 064029 (2010). [DOI], [ADS], [arXiv:0802.1508 [gr-qc]].
|
| * | 294 | Levi, M., “Binary dynamics from spin1-spin2 coupling at fourth post-Newtonian order”, Phys.
Rev. D, 85, 064043 (2012). [DOI], [ADS], [arXiv:1107.4322].
|
| * | 295 | Levi, M. and Steinhoff, J., “Equivalence of ADM Hamiltonian and Effective Field Theory
approaches at next-to-next-to-leading order spin1-spin2 coupling of binary inspirals”, J.
Cosmol. Astropart. Phys., 2014(12), 003 (2014). [DOI], [arXiv:1408.5762 [gr-qc]].
|
| * | 296 | Levi, M. and Steinhoff, J., “Leading order finite size effects with spins for inspiralling compact
binaries”, J. High Energy Phys., 2015(06), 059 (2015). [DOI], [arXiv:1410.2601 [gr-qc]].
|
| * | 297 | Levi, M. and Steinhoff, J., “Next-to-next-to-leading order gravitational spin-orbit coupling via
the effective field theory for spinning objects in the post-Newtonian scheme”, arXiv, e-print,
(2015). [arXiv:1506.05056 [gr-qc]].
|
| * | 298 | Levi, M. and Steinhoff, J., “Next-to-next-to-leading order gravitational spin-squared potential
via the effective field theory for spinning objects in the post-Newtonian scheme”, arXiv, e-print,
(2015). [arXiv:1506.05794 [gr-qc]].
|
| * | 299 | Levi, M. and Steinhoff, J., “Spinning gravitating objects in the effective field theory in the
post-Newtonian scheme”, J. High Energy Phys., 2015(09), 219 (2015). [DOI], [arXiv:1501.04956
[gr-qc]].
|
| * | 300 | Lidov, M. L., “The evolution of orbits of artificial satellites of planets under the action of
gravitational perturbations of external bodies”, Planet. Space Sci., 9, 719 (1962). [DOI].
|
| * | 301 | Limousin, F., Gondek-Rosinska, D. and Gourgoulhon, E., “Last orbits of binary strange quark
stars”, Phys. Rev. D, 71, 064012 (2005). [DOI], [ADS], [arXiv:gr-qc/0411127 [gr-qc]].
|
| * | 302 | Lincoln, C. W. and Will, C. M., “Coalescing binary systems of compact objects to
(post)5∕2-Newtonian order: Late-time evolution and gravitational-radiation emission”, Phys.
Rev. D, 42, 1123–1143 (1990). [DOI], [ADS].
|
| * | 303 | Lorentz, H. A. and Droste, J., “The motion of a system of bodies under the influence of their
mutual attraction, according to Einstein’s theory”, in The Collected Papers of H.A. Lorentz,
Vol. 5, pp. 330–355, (Nijhoff, The Hague, 1937). [DOI], Translated from Versl. K. Akad. Wet.
Amsterdam, 26, 392 and 649 (1917).
|
| * | 304 | Madore, J., “Gravitational radiation from a bounded source. I”, Ann. Inst. Henri Poincare,
12, 285–305 (1970). Online version (accessed 6 October 2013): http://www.numdam.org/item?id=AIHPA_1970__12_3_285_0.
|
| * | 305 | Marsat, S., “Cubic order spin effects in the dynamics and gravitational wave energy flux of
compact object binaries”, Class. Quantum Grav., 32, 085008 (2015). [DOI], [arXiv:1411.4118
[gr-qc]].
|
| * | 306 | Marsat, S., Bohé, A., Blanchet, L. and Buonanno, A., “Next-to-leading tail-induced spin-orbit
effects in the gravitational radiation of compact binaries”, Class. Quantum Grav., 31, 025023
(2013). [DOI], [arXiv:1307.6793 [gr-qc]].
|
| * | 307 | Marsat, S., Bohé, A., Faye, G. and Blanchet, L., “Next-to-next-to-leading order spin-orbit
effects in the equations of motion of compact binary systems”, Class. Quantum Grav., 30,
055007 (2013). [DOI], [arXiv:1210.4143].
|
| * | 308 | Martin, J. and Sanz, J. L., “Slow motion approximation in predictive relativistic mechanics.
II. Non-interaction theorem for interactions derived from the classical field-theory”, J. Math.
Phys., 20, 25–34 (1979). [DOI].
|
| * | 309 | Mathews, J., “Gravitational multipole radiation”, J. Soc. Ind. Appl. Math., 10, 768–780 (1962).
[DOI].
|
| * | 310 | Mathisson, M., “Republication of: New mechanics of material systems”, Gen. Relativ. Gravit.,
42, 1011–1048 (2010). [DOI].
|
| * | 311 | McClintock, J. E., Shafee, R., Narayan, R., Remillard, R. A., Davis, S. W. and Li, L.-X.,
“The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105”, Astrophys. J., 652, 518–539
(2006). [DOI], [ADS], [arXiv:astro-ph/0606076].
|
| * | 312 | Memmesheimer, R., Gopakumar, A. and Schäfer, G., “Third post-Newtonian accurate
generalized quasi-Keplerian parametrization for compact binaries in eccentric orbits”, Phys.
Rev. D, 70, 104011 (2004). [DOI], [gr-qc/0407049].
|
| * | 313 | Merritt, D., Milosavljević, M., Favata, M., Hughes, S. A. and Holz, D. E., “Consequences
of Gravitational Radiation Recoil”, Astrophys. J. Lett., 607, L9–L12 (2004). [DOI], [ADS],
[astro-ph/0402057].
|
| * | 314 | Mikóczi, B., Vasúth, M. and Gergely, L.Á., “Self-interaction spin effects in inspiralling
compact binaries”, Phys. Rev. D, 71, 124043 (2005). [DOI], [astro-ph/0504538].
|
| * | 315 | Miller, M. C. and Hamilton, D. P., “Four-Body Effects in Globular Cluster Black Hole
Coalescence”, Astrophys. J., 576, 894 (2002). [DOI], [astro-ph/0202298].
|
| * | 316 | Mino, Y., Sasaki, M., Shibata, M., Tagoshi, H. and Tanaka, T., “Black Hole Perturbation”,
Prog. Theor. Phys. Suppl., 128, 1–121 (1997). [DOI], [gr-qc/9712057].
|
| * | 317 | Mino, Y., Sasaki, M. and Tanaka, T., “Gravitational radiation reaction to a particle motion”,
Phys. Rev. D, 55, 3457–3476 (1997). [DOI], [arXiv:gr-qc/9606018].
|
| * | 318 | Mirshekari, S. and Will, C. M., “Compact binary systems in scalar-tensor gravity: Equations
of motion to 2.5 post-Newtonian order”, Phys. Rev. D, 87, 084070 (2013). [DOI], [ADS],
[arXiv:1301.4680 [gr-qc]].
|
| * | 319 | Misner, C. W., Thorne, K. S. and Wheeler, J. A., Gravitation, (W. H. Freeman, San Francisco,
1973). [ADS].
|
| * | 320 | Mora,
T. and Will, C. M., “Post-Newtonian diagnostic of quasi-equilibrium binary configurations of
compact objects”, Phys. Rev. D, 69, 104021 (2004). [DOI], [arXiv:gr-qc/0312082].
|
| * | 321 | Moritz, H., Advanced Physical Geodesy, (H. Wichmann, Karlsruhe, 1980). |
| * | 322 | Nissanke, S. and Blanchet, L., “Gravitational radiation reaction in the equations of motion of
compact binaries to 3.5 post-Newtonian order”, Class. Quantum Grav., 22, 1007–1031 (2005).
[DOI], [gr-qc/0412018].
|
| * | 323 | Nowak, M. A., Wilms, J., Pottschmidt, K., Schulz, N., Miller, J. and Maitra, D., “Suzaku
observations of 4U 1957+11: The most rapidly spinning black hole in the galaxy?”, in Petre,
R., Mitsuda, K. and Angelini, L., eds., SUZAKU 2011. Exploring the X-ray Universe: Suzaku
and Beyond (SUZAKU 2011), Palo Alto, California, USA, 20 – 22 July 2011, AIP Conference
Proceedings, 1427, pp. 48–51, (AIP Publishing, Melville, NY, 2012). [DOI], [ADS].
|
| * | 324 | Ohta, T., Okamura, H., Kimura, T. and Hiida, K., “Physically acceptable solution of Einstein’s
equation for many-body system”, Prog. Theor. Phys., 50, 492–514 (1973). [DOI].
|
| * | 325 | Ohta, T., Okamura, H., Kimura, T. and Hiida, K., “Coordinate Condition and Higher Order
Gravitational Potential in Canocical Formalism”, Prog. Theor. Phys., 51, 1598–1612 (1974).
[DOI].
|
| * | 326 | Ohta, T., Okamura, H., Kimura, T. and Hiida, K., “Higher-order gravitational potential for
many-body system”, Prog. Theor. Phys., 51, 1220–1238 (1974). [DOI].
|
| * | 327 | Okamura, H., Ohta, T., Kimura, T. and Hiida, K., “Perturbation calculation of gravitational
potentials”, Prog. Theor. Phys., 50, 2066–2079 (1973). [DOI].
|
| * | 328 | Owen, B. J., Tagoshi, H. and Ohashi, A., “Nonprecessional spin-orbit effects on gravitational
waves from inspiraling compact binaries to second post-Newtonian order”, Phys. Rev. D, 57,
6168–6175 (1998). [DOI], [gr-qc/9710134].
|
| * | 329 | Pan, Y., Buonanno, A., Buchman, L. T., Chu, T., Kidder, L. E., Pfeiffer, H. P. and
Scheel, M. A., “Effective-one-body waveforms calibrated to numerical relativity simulations:
Coalescence of non-precessing, spinning, equal-mass black holes”, Phys. Rev. D, 81, 084041
(2010). [DOI], [ADS], [arXiv:0912.3466 [gr-qc]].
|
| * | 330 | Papapetrou, A., “Equations of motion in general relativity”, Proc. Phys. Soc. London, Sect. B, 64, 57–75 (1951). |
| * | 331 | Papapetrou, A., “Spinning Test-Particles in General Relativity. I”, Proc. R. Soc. London, Ser.
A, 209, 248–258 (1951). [DOI].
|
| * | 332 | Papapetrou, A., “Relativité – une formule pour le rayonnement gravitationnel en première approximation”, C. R. Acad. Sci. Ser. II, 255, 1578 (1962). |
| * | 333 | Papapetrou, A., “Étude systématique du rayonnement gravitationnel 4-polaire. Énergie-impulsion et moment cinétique du rayonnement”, Ann. Inst. Henri Poincare, XIV, 79 (1971). |
| * | 334 | Papapetrou, A. and Linet, B., “Equation of motion including the reaction of gravitational
radiation”, Gen. Relativ. Gravit., 13, 335 (1981). [DOI].
|
| * | 335 | Pati, M. E. and Will, C. M., “Post-Newtonian gravitational radiation and equations of motion
via direct integration of the relaxed Einstein equations: Foundations”, Phys. Rev. D, 62, 124015
(2000). [DOI], [gr-qc/0007087].
|
| * | 336 | Pati, M. E. and Will, C. M., “Post-Newtonian gravitational radiation and equations of motion
via direct integration of the relaxed Einstein equations. II. Two-body equations of motion to
second post-Newtonian order, and radiation reaction to 3.5 post-Newtonian order”, Phys. Rev.
D, 65, 104008 (2002). [DOI], [ADS], [gr-qc/0201001].
|
| * | 337 | Penrose, R., “Asymptotic Properties of Fields and Space-Times”, Phys. Rev. Lett., 10, 66–68
(1963). [DOI], [ADS].
|
| * | 338 | Penrose, R., “Zero Rest-Mass Fields Including Gravitation: Asymptotic Behaviour”, Proc. R.
Soc. London, Ser. A, 284, 159–203 (1965). [DOI], [ADS].
|
| * | 339 | Peters, P. C., “Gravitational Radiation and the Motion of Two Point Masses”, Phys. Rev.,
136, B1224–B1232 (1964). [DOI], [ADS].
|
| * | 340 | Peters, P. C. and Mathews, J., “Gravitational Radiation from Point Masses in a Keplerian
Orbit”, Phys. Rev., 131, 435–440 (1963). [DOI], [ADS].
|
| * | 341 | Petrova, N. M., “Ob Uravnenii Dvizheniya i Tenzore Materii dlya Sistemy Konechnykh Mass v Obshchei Teorii Otnositielnosti”, J. Exp. Theor. Phys., 19(11), 989–999 (1949). |
| * | 342 | Pfeiffer, H. P., Teukolsky, S. A. and Cook, G. B., “Quasicircular orbits for spinning binary
black holes”, Phys. Rev. D, 62, 104018 (2000). [DOI], [ADS], [gr-qc/0006084].
|
| * | 343 | Pirani, F. A. E., “Introduction to Gravitational Radiation Theory”, in Trautman, A., Pirani,
F. A. E. and Bondi, H., eds., Lectures on General Relativity, Vol. 1, Brandeis Summer Institute
in Theoretical Physics 1964, pp. 249–373, (Prentice-Hall, Englewood Cliffs, NJ, 1965). [ADS].
|
| * | 344 | Plebański, J. F. and Bażański, S. L., “The general Fokker action principle and its application in general relativity theory”, Acta Phys. Pol., 18, 307–345 (1959). |
| * | 345 | Poisson, E., “Gravitational radiation from a particle in circular orbit around a black hole. I.
Analytic results for the nonrotating case”, Phys. Rev. D, 47, 1497–1510 (1993). [DOI], [ADS].
|
| * | 346 | Poisson, E., “Gravitational radiation from a particle in circular orbit around a black-hole.
VI. Accuracy of the post-Newtonian expansion”, Phys. Rev. D, 52, 5719–5723 (1995). [DOI],
[gr-qc/9505030]. Erratum: Phys. Rev. D, 55, 7980 (1997).
|
| * | 347 | Poisson, E., “Gravitational waves from inspiraling compact binaries: The quadrupole-moment
term”, Phys. Rev. D, 57, 5287–5290 (1997). [DOI], [gr-qc/9709032].
|
| * | 348 | Poisson, E., Pound, A. and Vega, I., “The Motion of Point Particles in Curved Spacetime”,
Living Rev. Relativity, 14, lrr-2011-7 (2011). [DOI], [ADS], [arXiv:1102.0529 [gr-qc]]. URL
(accessed 6 October 2013): http://www.livingreviews.org/lrr-2011-7. |
| * | 349 | Poisson, E. and Sasaki, M., “Gravitational radiation from a particle in circular orbit around a
black hole. V. Black-hole absorption and tail corrections”, Phys. Rev. D, 51, 5753–5767 (1995).
[DOI], [gr-qc/9412027].
|
| * | 350 | Poisson, E. and Will, C. M., “Gravitational waves from inspiraling compact binaries: Parameter
estimation using second-post-Newtonian wave forms”, Phys. Rev. D, 52, 848–855 (1995). [DOI],
[arXiv:gr-qc/9502040].
|
| * | 351 | Porto, R. A., “Post-Newtonian corrections to the motion of spinning bodies in NRGR”, Phys.
Rev. D, 73, 104031 (2006). [DOI], [gr-qc/0511061].
|
| * | 352 | Porto, R. A., “Next-to-leading-order spin–orbit effects in the motion of inspiralling compact
binaries”, Class. Quantum Grav., 27, 205001 (2010). [DOI], [arXiv:1005.5730 [gr-qc]].
|
| * | 353 | Porto, R. A., Ross, A. and Rothstein, I. Z., “Spin induced multipole moments for the
gravitational wave flux from binary inspirals to third Post-Newtonian order”, J. Cosmol.
Astropart. Phys., 2011(3), 009 (2011). [DOI], [arXiv:1007.1312 [gr-qc]].
|
| * | 354 | Porto, R. A. and Rothstein, I. Z., “Calculation of the first nonlinear contribution to the
general-relativistic spin-spin interaction for binary systems”, Phys. Rev. Lett., 97, 021101
(2006). [DOI], [arXiv:gr-qc/0604099].
|
| * | 355 | Porto, R. A. and Rothstein, I. Z., “Next to leading order spin(1)spin(1) effects in the motion of
inspiralling compact binaries”, Phys. Rev. D, 78, 044013 (2008). [DOI], [ADS], [arXiv:0804.0260
[gr-qc]].
|
| * | 356 | Porto, R. A. and Rothstein, I. Z., “Spin(1)spin(2) effects in the motion of inspiralling compact
binaries at third order in the post-Newtonian expansion”, Phys. Rev. D, 78, 044012 (2008).
[DOI], [arXiv:0802.0720 [gr-qc]].
|
| * | 357 | Poujade, O. and Blanchet, L., “Post-Newtonian approximation for isolated systems calculated
by matched asymptotic expansions”, Phys. Rev. D, 65, 124020 (2002). [DOI], [gr-qc/0112057].
|
| * | 358 | Press, W. H., “Gravitational Radiation from Sources Which Extend Into Their Own Wave
Zone”, Phys. Rev. D, 15, 965–968 (1977). [DOI].
|
| * | 359 | Pretorius, F., “Evolution of Binary Black-Hole Spacetimes”, Phys. Rev. Lett., 95, 121101
(2005). [DOI], [ADS], [arXiv:gr-qc/0507014].
|
| * | 360 | Quinn, T. C. and Wald, R. M., “Axiomatic approach to electromagnetic and gravitational
radiation reaction of particles in curved spacetime”, Phys. Rev. D, 56, 3381–3394 (1997). [DOI],
[arXiv:gr-qc/9610053].
|
| * | 361 | Rendall, A. D., “Convergent and divergent perturbation series and the post-Minkowskian
scheme”, Class. Quantum Grav., 7, 803 (1990). [DOI].
|
| * | 362 | Rendall, A. D., “On the definition of post-Newtonian approximations”, Proc. R. Soc. London,
Ser. A, 438, 341–360 (1992). [DOI].
|
| * | 363 | Rendall, A. D., “The Newtonian limit for asymptotically flat solutions of the Einstein-Vlasov
system”, Commun. Math. Phys., 163, 89–112 (1994). [DOI], [gr-qc/9303027].
|
| * | 364 | Reynolds, C. S., “Measuring Black Hole Spin Using X-Ray Reflection Spectroscopy”, Space
Sci. Rev., 183, 277–294 (2014). [DOI], [ADS], [arXiv:1302.3260 [astro-ph.HE]].
|
| * | 365 | Riesz, M., “L’intégrale de Riemann–Liouville et le problème de Cauchy”, Acta Math., 81,
1–218 (1949). [DOI].
|
| * | 366 | Rieth, R. and Schäfer, G., “Spin and tail effects in the gravitational-wave emission of compact
binaries”, Class. Quantum Grav., 14, 2357 (1997). [DOI].
|
| * | 367 | Sachs, R. K., “Gravitational waves in general relativity. VI. The outgoing radiation condition”,
Proc. R. Soc. London, Ser. A, 264, 309–338 (1961). [DOI].
|
| * | 368 | Sachs, R. K., “Gravitational Waves in General Relativity. VIII. Waves in Asymptotically Flat
Space-Time”, Proc. R. Soc. London, Ser. A, 270, 103–126 (1962). [DOI], [ADS].
|
| * | 369 | Sachs, R. K. and Bergmann, P. G., “Structure of Particles in Linearized Gravitational
Theory”, Phys. Rev., 112, 674–680 (1958). [DOI].
|
| * | 370 | Sago, N., Barack, L. and Detweiler, S., “Two approaches for the gravitational self force in black
hole spacetime: Comparison of numerical results”, Phys. Rev. D, 78, 124024 (2008). [DOI],
[arXiv:0810.2530].
|
| * | 371 | Santamaría, L. et al., “Matching post-Newtonian and numerical relativity waveforms:
Systematic errors and a new phenomenological model for non-precessing black hole binaries”,
Phys. Rev. D, 82, 064016 (2010). [DOI], [ADS], [arXiv:1005.3306 [gr-qc]].
|
| * | 372 | Sasaki, M., “Post-Newtonian Expansion of the Ingoing-Wave Regge-Wheeler Function”, Prog.
Theor. Phys., 92, 17–36 (1994). [DOI].
|
| * | 373 | Sasaki, M. and Tagoshi, H., “Analytic Black Hole Perturbation Approach to Gravitational
Radiation”, Living Rev. Relativity, 6, lrr-2003-6 (2003). [DOI], [ADS], [arXiv:gr-qc/0306120].
URL (accessed 6 October 2013): http://www.livingreviews.org/lrr-2003-6. |
| * | 374 | Schäfer, G., “Acceleration-dependent Lagrangians in general relativity”, Phys. Lett. A, 100,
128 (1984). [DOI].
|
| * | 375 | Schäfer, G., “The Gravitational Quadrupole Radiation-Reaction Force and the Canonical
Formalism of ADM”, Ann. Phys. (N.Y.), 161, 81–100 (1985). [DOI].
|
| * | 376 | Schäfer, G., “The ADM Hamiltonian at the Postlinear Approximation”, Gen. Relativ. Gravit.,
18, 255–270 (1986). [DOI].
|
| * | 377 | Schäfer, G., “Three-body Hamiltonian in general relativity”, Phys. Lett., 123, 336–339 (1987).
[DOI].
|
| * | 378 | Schäfer, G., “Post-Newtonian Methods: Analytic Results on the Binary Problem”, in
Blanchet, L., Spallicci, A. and Whiting, B., eds., Mass and Motion in General Relativity,
Lectures from the CNRS School on Mass held in Orléans, France, 23 – 25 June 2008,
Fundamental Theories of Physics, 162, pp. 167–210, (Springer, Dordrecht; New York, 2011).
[DOI], [ADS].
|
| * | 379 | Schäfer, G. and Wex, N., “Second post-Newtonian motion of compact binaries”, Phys. Lett.
A, 174, 196–205 (1993). [DOI]. Erratum: Phys. Lett. A, 177, 461 (1993).
|
| * | 380 | Schwartz, L., “Sur l’impossibilité de la multiplication des distributions”, C. R. Acad. Sci. Ser. II, 239, 847–848 (1954). |
| * | 381 | Schwartz, L., Théorie des distributions, (Hermann, Paris, 1978). |
| * | 382 | Sellier, A., “Hadamard’s finite part concept in dimension n ≥ 2, distributional definition,
regularization forms and distributional derivatives”, Proc. R. Soc. London, Ser. A, 445, 69–98
(1994). [DOI].
|
| * | 383 | Shah, A., Friedmann, J. and Whiting, B. F., “Finding high-order analytic post-Newtonian
parameters from a high-precision numerical self-force calculation”, Phys. Rev. D, 89, 064042
(2014). [DOI], [arXiv:1312.1952 [gr-qc]].
|
| * | 384 | Simon, W. and Beig, R., “The multipole structure of stationary space-times”, J. Math. Phys.,
24, 1163–1171 (1983). [DOI].
|
| * | 385 | Sopuerta, C. F., Yunes, N. and Laguna, P., “Gravitational Recoil from Binary Black
Hole Mergers: the Close-Limit Approximation”, Phys. Rev. D, 74, 124010 (2006). [DOI],
[astro-ph/0608600].
|
| * | 386 | Steinhoff, J., “Canonical formulation of spin in general relativity”, Ann. Phys. (Berlin), 523,
296 (2011). [DOI], [arXiv:1106.4203 [gr-qc]].
|
| * | 387 | Steinhoff, J., Hergt, S. and Schäfer, G., “Next-to-leading order gravitational spin(1)-spin(2)
dynamics in Hamiltonian form”, Phys. Rev. D, 77, 081501(R) (2008). [arXiv:0712.1716 [gr-qc]].
|
| * | 388 | Steinhoff, J., Hergt, S. and Schäfer, G., “Spin-squared Hamiltonian of next-to-leading order
gravitational interaction”, Phys. Rev. D, 78, 101503(R) (2008). [arXiv:0809.2200 [gr-qc]].
|
| * | 389 | Steinhoff, J., Schäfer, G. and Hergt, S., “ADM canonical formalism for gravitating spinning
objects”, Phys. Rev. D, 77, 104018 (2008). [DOI], [arXiv:0805.3136 [gr-qc]].
|
| * | 390 | Strohmayer, T. E., “Discovery of a 450 Hz quasi-periodic oscillation from the microquasar
GRO J1655–40 with the Rossi X-ray Timing Explorer”, Astrophys. J. Lett., 552, L49–L53
(2001). [DOI], [ADS].
|
| * | 391 | ’t Hooft, G. and Veltman, M., “Regularization and renormalization of gauge fields”, Nucl.
Phys. B, 44, 139 (1972). [DOI].
|
| * | 392 | Tagoshi, H., Mano, S. and Takasugi, E., “Post-Newtonian Expansion of Gravitational Waves
from a Particle in Circular Orbits around a Rotating Black Hole”, Prog. Theor. Phys., 98, 829
(1997). [DOI], [gr-qc/9711072].
|
| * | 393 | Tagoshi, H. and Nakamura, T., “Gravitational waves from a point particle in circular orbit
around a black hole: Logarithmic terms in the post-Newtonian expansion”, Phys. Rev. D, 49,
4016–4022 (1994). [DOI].
|
| * | 394 | Tagoshi, H., Ohashi, A. and Owen, B. J., “Gravitational field and equations of motion of
spinning compact binaries to 2.5-post-Newtonian order”, Phys. Rev. D, 63, 044006 (2001).
[DOI], [gr-qc/0010014].
|
| * | 395 | Tagoshi, H. and Sasaki, M., “Post-Newtonian Expansion of Gravitational Waves from a Particle
in Circular Orbit around a Schwarzschild Black Hole”, Prog. Theor. Phys., 92, 745–771 (1994).
[DOI], [gr-qc/9405062].
|
| * | 396 | Tagoshi, H., Shibata, M., Tanaka, T. and Sasaki, M., “Post-Newtonian expansion of
gravitational waves from a particle in circular orbit around a rotating black hole: Up to O(v8)
beyond the quadrupole formula”, Phys. Rev. D, 54, 1439–1459 (1996). [DOI].
|
| * | 397 | Tanaka, T., Tagoshi, H. and Sasaki, M., “Gravitational Waves by a Particle in Circular Orbit
around a Schwarzschild Black Hole: 5.5 Post-Newtonian Formula”, Prog. Theor. Phys., 96,
1087–1101 (1996). [DOI], [gr-qc/9701050].
|
| * | 398 | Taylor, J. H., “Pulsar timing and relativistic gravity”, Class. Quantum Grav., 10, 167–174
(1993). [DOI].
|
| * | 399 | Taylor, J. H., Fowler, L. A. and McCulloch, P. M., “Measurements of general relativistic
effects in the binary pulsar PSR 1913+16”, Nature, 277, 437–440 (1979). [DOI].
|
| * | 400 | Taylor, J. H. and Weisberg, J. M., “A New Test of General Relativity: Gravitational Radiation
and the Binary Pulsar PSR 1913+16”, Astrophys. J., 253, 908–920 (1982). [DOI].
|
| * | 401 | Tessmer, M. and Schäfer, G., “Full-analytic frequency-domain 1PN-accurate gravitational
wave forms from eccentric compact binaries”, Phys. Rev. D, 82, 124064 (2010). [DOI],
[arXiv:1006.3714 [gr-qc]].
|
| * | 402 | Tessmer, M. and Schäfer, G., “Full-analytic frequency-domain gravitational wave forms from
eccentric compact binaries to 2PN accuracy”, Ann. Phys. (Berlin), 523, 813 (2011). [DOI],
[arXiv:1012.3894 [gr-qc]].
|
| * | 403 | Thorne, K. S., “Multipole expansions of gravitational radiation”, Rev. Mod. Phys., 52, 299–339
(1980). [DOI], [ADS].
|
| * | 404 | Thorne, K. S., “The theory of gravitational radiation: An introductory review”, in Deruelle, N. and Piran, T., eds., Gravitational Radiation, NATO Advanced Study Institute, Centre de physique des Houches, 2 – 21 June 1982, pp. 1–57, (North-Holland; Elsevier, Amsterdam; New York, 1983). |
| * | 405 | Thorne, K. S., “Gravitational radiation”, in Hawking, S. W. and Israel, W., eds., Three
Hundred Years of Gravitation, pp. 330–458, (Cambridge University Press, Cambridge; New
York, 1987). [Google Books].
|
| * | 406 | Thorne, K. S., “Gravitational-wave bursts with memory: The Christodoulou effect”, Phys.
Rev. D, 45, 520 (1992). [DOI].
|
| * | 407 | Thorne, K. S. and Hartle, J. B., “Laws of motion and precession for black holes and other
bodies”, Phys. Rev. D, 31, 1815–1837 (1985). [DOI].
|
| * | 408 | Thorne, K. S. and Kovàcs, S. J., “Generation of gravitational waves. I. Weak-field sources”,
Astrophys. J., 200, 245–262 (1975). [DOI].
|
| * | 409 | Trautman, A., “Lectures on General Relativity”, Gen. Relativ. Gravit., 34, 721–762 (2002).
[DOI]. Lectures delivered at King’s College in London in May – June 1958.
|
| * | 410 | Trias, M. and Sintes, A. M., “LISA observations of supermassive black holes: Parameter
estimation using full post-Newtonian inspiral waveforms”, Phys. Rev. D, 77, 024030 (2008).
[DOI], [ADS], [arXiv:0707.4434 [gr-qc]].
|
| * | 411 | Tulczyjew, W., “On the energy-momentum tensor density for simple pole particles”, Bull. Acad. Polon. Sci. Cl. III, 5, 279 (1957). |
| * | 412 | Tulczyjew, W., “Motion of multipole particles in general relativity theory”, Acta Phys. Pol., 18, 37 (1959). |
| * | 413 | Vaidya, V., “Gravitational spin Hamiltonians from the S matrix”, Phys. Rev. D, 91, 024017
(2015). [DOI], [arXiv:1410.5348 [hep-th]].
|
| * | 414 | Vines, J., Hinderer, T. and Flanagan, É.É., “Post-1-Newtonian tidal effects in the
gravitational waveform from binary inspirals”, Phys. Rev. D, 83, 084051 (2011). [DOI],
[arXiv:1101.1673 [gr-qc]].
|
| * | 415 | Wagoner, R. V., “Test for Existence of Gravitational Radiation”, Astrophys. J. Lett., 196,
L63–L65 (1975). [DOI].
|
| * | 416 | Wagoner, R. V. and Will, C. M., “Post-Newtonian gravitational radiation from orbiting point
masses”, Astrophys. J., 210, 764–775 (1976). [DOI].
|
| * | 417 | Wald, R. M., “On perturbations of a Kerr black hole”, J. Math. Phys., 14, 1453–1461 (1973).
[DOI].
|
| * | 418 | Walker, M. and Will, C. M., “The approximation of radiative effects in relativistic gravity:
Gravitational radiation reaction and energy loss in nearly Newtonian systems”, Astrophys. J.
Lett., 242, L129–L133 (1980). [DOI], [ADS].
|
| * | 419 | Wen, L., “On the Eccentricity Distribution of Coalescing Black Hole Binaries Driven
by the Kozai Mechanism in Globular Clusters”, Astrophys. J., 598, 419 (2003). [DOI],
[astro-ph/0211492].
|
| * | 420 | Wex, N., “The second post-Newtonian motion of compact binary-star systems with spin”,
Class. Quantum Grav., 12, 983–1005 (1995). [DOI].
|
| * | 421 | Will, C. M., “Gravitational Waves from Inspiralling Compact Binaries:
A Post-Newtonian Approach”, in Sasaki, M., ed., Relativistic Cosmology, Proceedings of the
8th Nishinomiya-Yukawa Memorial Symposium, Shukugawa City Hall, Nishinomiya, Hyogo,
Japan, 28 – 29 October, 1993, NYMSS, 8, pp. 83–98, (Universal Academy Press, Tokyo, 1993).
[gr-qc/9403033].
|
| * | 422 | Will, C. M., “Generation of post-Newtonian gravitational radiation via direct integration
of the relaxed Einstein equations”, Prog. Theor. Phys. Suppl., 136, 158–167 (1999). [DOI],
[gr-qc/9910057].
|
| * | 423 | Will, C. M., “Post-Newtonian gravitational radiation and equations of motion via direct
integration of the relaxed Einstein equations. III. Radiation reaction for binary systems with
spinning bodies”, Phys. Rev. D, 71, 084027 (2005). [DOI], [gr-qc/0502039].
|
| * | 424 | Will, C. M. and Wiseman, A. G., “Gravitational radiation from compact binary systems:
Gravitational waveforms and energy loss to second post-Newtonian order”, Phys. Rev. D, 54,
4813–4848 (1996). [DOI], [gr-qc/9608012].
|
| * | 425 | Wiseman, A. G., “Coalescing binary systems of compact objects to (post)5∕2-Newtonian order.
II. Higher-order wave forms and radiation recoil”, Phys. Rev. D, 46, 1517–1539 (1992). [DOI],
[ADS].
|
| * | 426 | Wiseman, A. G., “Coalescing binary systems of compact objects to (post)5∕2-Newtonian order.
IV. The gravitational wave tail”, Phys. Rev. D, 48, 4757–4770 (1993). [DOI], [ADS].
|
| * | 427 | Wiseman, A. G. and Will, C. M., “Christodoulou’s nonlinear gravitational-wave memory:
Evaluation in the quadrupole approximation”, Phys. Rev. D, 44, R2945–R2949 (1991). [DOI].
|
| * | 428 | Zeng, J. and Will, C. M., “Application of energy and angular momentum balance to
gravitational radiation reaction for binary systems with spin-orbit coupling”, Gen. Relativ.
Gravit., 39, 1661 (2007). [DOI], [arXiv:0704.2720].
|