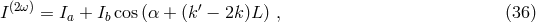3 Quantum-Spacetime Phenomenology of UV Corrections to Lorentz Symmetry
The largest area of quantum-spacetime-phenomenology research concerns the fate of Lorentz (/Poincaré) symmetry at the Planck scale, focusing on the idea that the conjectured new effects might become manifest at low energies (the particle energies accessible to us, which are much below the Planck scale) in the form of “UV corrections”, correction terms with powers of energy in the numerator and powers of the Planck scale in the denominator.Among the possible effects that might signal departures from Lorentz/Poincaré symmetry, the interest has been predominantly directed toward the study of the form of the energy-momentum (dispersion) relation. This was due both to the (relative) robustness of associated theory results in quantum-spacetime research and to the availability of very valuable opportunities of related data analyses. Indeed, as several examples in this section will show, over the last decade there were very significant improvements of the sensitivity of Lorentz- and Poincaré-symmetry tests.
Before discussing some actual phenomenological analyses, I find it appropriate to start this section with some preparatory work. This will include some comments on the “Minkowski limit of Quantum Gravity”, which I have already referred to but should be discussed a bit more carefully. And I shall also give a rather broad perspective on the quantum-spacetime implications for the set up of test theories suitable for the study of the fate of Lorentz/Poincaré symmetry at the Planck scale.
3.1 Some relevant concepts
3.1.1 The Minkowski limit
In our current conceptual framework Poincaré symmetry emerges in situations that allow the adoption of a Minkowski metric throughout. These situations could be described as the “classical Minkowski limit”.
It is not inconceivable that quantum gravity might admit a limit in which one can assume throughout a (expectation value of the) metric of Minkowski type, but some Planck-scale features of the fundamental description of spacetime (such as spacetime discreteness and/or spacetime noncommutativity) are still not completely negligible. This “nontrivial Minkowski limit” would be such that essentially the role of the Planck scale in the description of gravitational phenomena can be ignored (so that indeed one can make reference to a fixed Minkowski metric), but the possible role of the Planck scale in spacetime structure/kinematics is still significant. This intuition inspires the work on quantum-Minkowski spacetimes, and the analysis of the symmetries of these quantum spacetimes.
It is not obvious that the correct quantum gravity should admit such a nontrivial Minkowski limit. With the little we presently know about the quantum-gravity problem we must be open to the possibility that the Minkowski limit could actually be trivial, i.e., that whenever the role of the Planck scale in the description of gravitational phenomena can be neglected (and the metric is Minkowskian at least on average) one should also neglect the role of the Planck scale in spacetime structure. But the hypothesis of a nontrivial Minkowski limit is worth exploring: it is a plausible hypothesis and it would be extremely valuable for us if quantum gravity did admit such a limit, since it might open a wide range of opportunities for accessible experimental verification, as I shall stress in what follows.
When I mention a result on the theory side concerning the fate of Poincaré symmetry at the Planck scale clearly it must be the case that the authors have considered (or attempted to consider) the Minkowski limit of their preferred formalism.
3.1.2 Three perspectives on the fate of Lorentz symmetry at the Planck scale
It is fair to state that each quantum-gravity research line can be connected with one of three perspectives on the problem: the particle-physics perspective, the GR perspective and the condensed-matter perspective.
From a particle-physics perspective it is natural to attempt to reproduce as much as possible the successes of the Standard Model of particle physics. One is tempted to see gravity simply as one more gauge interaction. From this particle-physics perspective a natural solution of the quantum-gravity problem should have its core features described in terms of graviton-like exchange in a background classical spacetime. Indeed this structure is found in string theory, the most developed among the quantum-gravity approaches that originate from a particle-physics perspective.
The particle-physics perspective provides no a priori reasons to renounce Poincaré symmetry, since
Minkowski classical spacetime is an admissible background spacetime, and in classical Minkowski there
cannot be any a priori obstruction for classical Poincaré symmetry. Still, a breakdown of Lorentz
symmetry, in the sense of spontaneous symmetry breaking, is possible, and this possibility has been studied
extensively over the last few years, especially in string theory (see, e.g., Ref. [347 , 213
, 213 ] and references
therein).
] and references
therein).
Complementary to the particle-physics perspective is the GR perspective, whose core characteristic
is the intuition that one should firmly reject the possibility of relying on a background
spacetime [476, 502]. According to GR the evolution of particles and the structure of spacetime are
self-consistently connected: rather than specify a spacetime arena (a spacetime background)
beforehand, the dynamical equations determine at once both the spacetime structure and the
evolution of particles. Although less publicized, there is also growing awareness of the fact that, in
addition to the concept of background independence, the development of GR relied heavily
on the careful consideration of the in-principle limitations that measurement procedures can
encounter.14
In light of the various arguments suggesting that, whenever both quantum mechanics and GR are taken into
account, there should be an in-principle Planck-scale limitation to the localization of a spacetime
point (an event), the GR perspective invites one to renounce any direct reference to a classical
spacetime [211, 20, 432 , 50
, 50 , 249
, 249 ]. Indeed, this requirement that spacetime be described as
fundamentally nonclassical (“fundamentally quantum”), so that the measurability limitations
be reflected by a corresponding measurability-limited formalization of spacetime, is another
element of intuition that is guiding quantum-gravity research from the GR perspective. This
naturally leads one to consider discretized spacetimes, as in the LQG approach or noncommutative
spacetimes.
]. Indeed, this requirement that spacetime be described as
fundamentally nonclassical (“fundamentally quantum”), so that the measurability limitations
be reflected by a corresponding measurability-limited formalization of spacetime, is another
element of intuition that is guiding quantum-gravity research from the GR perspective. This
naturally leads one to consider discretized spacetimes, as in the LQG approach or noncommutative
spacetimes.
Results obtained over the last few years indicate that this GR perspective naturally leads, through the emergence of spacetime discreteness and/or noncommutativity, to some departures from classical Poincaré symmetry. LQG and some other discretized-spacetime quantum-gravity approaches appear to require a description of the familiar (classical, continuous) Poincaré symmetry as an approximate symmetry, with departures governed by the Planck scale. And in the study of noncommutative spacetimes some Planck-scale departures from Poincaré symmetry appear to be inevitable.
The third possibility is a condensed-matter perspective on the quantum-gravity problem (see, e.g., Refs. [537, 358, 166]), in which spacetime itself is seen as a sort of emerging critical-point entity. Condensed-matter theories are used to describe the degrees of freedom that are measured in the laboratory as collective excitations within a theoretical framework, whose primary description is given in terms of much different, and often practically inaccessible, fundamental degrees of freedom. Close to a critical point some symmetries arise for the collective-excitation theory, which do not carry the significance of fundamental symmetries, and are, in fact, lost as soon as the theory is probed away from the critical point. Notably, some familiar systems are known to exhibit special-relativistic invariance in certain limits, even though, at a more fundamental level, they are described in terms of a nonrelativistic theory. So, from the condensed-matter perspective on the quantum-gravity problem it is natural to see the familiar classical continuous Poincaré symmetry only as an approximate symmetry.
Further encouragement for the idea of an emerging spacetime (though not necessarily invoking the condensed-matter perspective) comes from the realization [304, 533, 444] that the Einstein equations can be viewed as an equation of state, so in some sense thermodynamics implies GR and the associated microscopic theory might not look much like gravity.
3.1.3 Aside on broken versus deformed spacetime symmetries
If the fate of Poincaré symmetry at the Planck scale is nontrivial, the simplest possibility is the one of broken Poincaré symmetry, in the same sense that other symmetries are broken in physics. As mentioned, an example of a suitable mechanism is provided by the possibility that a tensor field might have a vacuum expectation value [347].
An alternative possibility, that in recent years has attracted the interest of a growing number of
researchers within the quantum-spacetime and the quantum-gravity communities, is the one of deformed
(rather than broken) spacetime symmetries, in the sense of the “doubly-special-relativity” (DSR) proposal I
put forward a few years ago [58 ]. I have elsewhere [63
]. I have elsewhere [63 ] attempted to expose the compellingness of this
possibility. Still, because of the purposes of this review, I must take into account that the development of
phenomenologically-viable DSR models is still in its infancy. In particular, several authors (see, e.g.,
Refs. [56, 493
] attempted to expose the compellingness of this
possibility. Still, because of the purposes of this review, I must take into account that the development of
phenomenologically-viable DSR models is still in its infancy. In particular, several authors (see, e.g.,
Refs. [56, 493 , 202, 292]) have highlighted the challenges for the description of spacetime and in particular
spacetime locality that inevitably arise when contemplating a DSR scenario. I am confident that some
of the most recent DSR studies, particularly those centered on the analysis of the “relative
locality” [71, 504, 88, 67
, 202, 292]) have highlighted the challenges for the description of spacetime and in particular
spacetime locality that inevitably arise when contemplating a DSR scenario. I am confident that some
of the most recent DSR studies, particularly those centered on the analysis of the “relative
locality” [71, 504, 88, 67 ], contain the core ideas that in due time will allow us to fully establish a robust
DSR picture of spacetime, but I nonetheless feel that we are still far from the possibility of developing a
robust DSR phenomenology.
], contain the core ideas that in due time will allow us to fully establish a robust
DSR picture of spacetime, but I nonetheless feel that we are still far from the possibility of developing a
robust DSR phenomenology.
Interested readers have available a rather sizable DSR literature (see, e.g.,
Ref. [58 , 55
, 55 , 349
, 349 , 140
, 140 , 386
, 386 , 387
, 387 , 354
, 354 , 388
, 388 , 352
, 352 , 353
, 353 , 350
, 350 , 26
, 26 , 200
, 200 , 493
, 493 , 465
, 465 , 291
, 291 , 314
, 314 , 366
, 366 ] and
references therein), but for the purposes of this review I shall limit my consideration of DSR ideas on
phenomenology to a single one of the (many) relevant issues, which is an observation that concerns the
compatibility between modifications of the energy-momentum dispersion relation and modifications of
the law of conservation of energy-momentum. My main task in this Section is to illustrate the
differences (in relation to this compatibility issue) between the broken-symmetry hypothesis and the
DSR-deformed-symmetry hypothesis.
] and
references therein), but for the purposes of this review I shall limit my consideration of DSR ideas on
phenomenology to a single one of the (many) relevant issues, which is an observation that concerns the
compatibility between modifications of the energy-momentum dispersion relation and modifications of
the law of conservation of energy-momentum. My main task in this Section is to illustrate the
differences (in relation to this compatibility issue) between the broken-symmetry hypothesis and the
DSR-deformed-symmetry hypothesis.
The DSR scenario was proposed [58 ] as a sort of alternative perspective on the results
on Planck-scale departures from Lorentz symmetry that had been reported in numerous
articles [66
] as a sort of alternative perspective on the results
on Planck-scale departures from Lorentz symmetry that had been reported in numerous
articles [66 , 247
, 247 , 327
, 327 , 38
, 38 , 73
, 73 , 463
, 463 , 33
, 33 ] between 1997 and 2000. These studies were advocating a
Planck-scale modification of the energy-momentum dispersion relation, usually of the form
] between 1997 and 2000. These studies were advocating a
Planck-scale modification of the energy-momentum dispersion relation, usually of the form
 , on the basis of preliminary findings in the analysis of several
formalisms in use for Planck-scale physics. The complexity of the formalisms is such that very little else was
known about their physical consequences, but the evidence of a modification of the dispersion relation was
becoming robust. In all of the relevant papers it was assumed that such modifications of the dispersion
relation would amount to a breakdown of Lorentz symmetry, with associated emergence of a preferred class
of inertial observers (usually identified with the natural observer of the cosmic microwave background
radiation).
, on the basis of preliminary findings in the analysis of several
formalisms in use for Planck-scale physics. The complexity of the formalisms is such that very little else was
known about their physical consequences, but the evidence of a modification of the dispersion relation was
becoming robust. In all of the relevant papers it was assumed that such modifications of the dispersion
relation would amount to a breakdown of Lorentz symmetry, with associated emergence of a preferred class
of inertial observers (usually identified with the natural observer of the cosmic microwave background
radiation).
However, it then turned out to be possible [58 ] to avoid this preferred-frame expectation, following a
line of analysis in many ways analogous to the one familiar from the developments that led to the
emergence of special relativity (SR), now more than a century ago. In Galileian relativity there is no
observer-independent scale, and in fact the energy-momentum relation is written as
] to avoid this preferred-frame expectation, following a
line of analysis in many ways analogous to the one familiar from the developments that led to the
emergence of special relativity (SR), now more than a century ago. In Galileian relativity there is no
observer-independent scale, and in fact the energy-momentum relation is written as 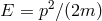 .
As experimental evidence in favor of Maxwell’s equations started to grow, the fact that those
equations involve a fundamental velocity scale appeared to require the introduction of a preferred
class of inertial observers. But in the end we discovered that the situation was not demanding
the introduction of a preferred frame, but rather a modification of the laws of transformation
between inertial observers. Einstein’s SR introduced the first observer-independent relativistic
scale (the velocity scale
.
As experimental evidence in favor of Maxwell’s equations started to grow, the fact that those
equations involve a fundamental velocity scale appeared to require the introduction of a preferred
class of inertial observers. But in the end we discovered that the situation was not demanding
the introduction of a preferred frame, but rather a modification of the laws of transformation
between inertial observers. Einstein’s SR introduced the first observer-independent relativistic
scale (the velocity scale  ), its dispersion relation takes the form
), its dispersion relation takes the form 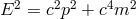 (in
which
(in
which  plays a crucial role in relation to dimensional analysis), and the presence of
plays a crucial role in relation to dimensional analysis), and the presence of  in
Maxwell’s equations is now understood as a manifestation of the necessity to deform the Galilei
transformations.
in
Maxwell’s equations is now understood as a manifestation of the necessity to deform the Galilei
transformations.
It is plausible that we might be presently confronted with an analogous scenario. Research in quantum
gravity is increasingly providing reasons for interest in Planck-scale modifications of the dispersion relation,
and, while it was customary to assume that this would amount to the introduction of a preferred class of
inertial frames (a “quantum-gravity ether”), the proper description of these new structures might require
yet again a modification of the laws of transformation between inertial observers. The new transformation
laws would have to be characterized by two scales ( and
and 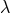 ) rather than the single one (
) rather than the single one ( ) of ordinary
SR.
) of ordinary
SR.
While the DSR idea came to be proposed in the context of studies of modifications of the dispersion
relation, one could have other uses for the second relativistic scale, as stressed in parts of the DSR
literature [58 , 55, 349, 140, 386, 387, 354, 388, 352, 353, 350, 26
, 55, 349, 140, 386, 387, 354, 388, 352, 353, 350, 26 , 200, 493, 465, 291, 314, 366].
Instead of promoting to the status of relativistic invariant a modified dispersion relation, one can have DSR
scenarios with undeformed dispersion relations but, for example, with an observer-independent bound on
the accuracy achievable in the measurement of distances [63
, 200, 493, 465, 291, 314, 366].
Instead of promoting to the status of relativistic invariant a modified dispersion relation, one can have DSR
scenarios with undeformed dispersion relations but, for example, with an observer-independent bound on
the accuracy achievable in the measurement of distances [63 ]. However, as announced, within the confines
of this quantum-spacetime-phenomenology review I shall only make use of one DSR argument, that applies
to cases in which indeed the dispersion relation is modified. This concerns the fact that in the presence of
observer-independent modifications of the dispersion relation (DSR-)relativistic invariance imposes the
presence of associated modifications of the law of energy-momentum conservation. More general discussions
of this issue are offered in Refs. [58
]. However, as announced, within the confines
of this quantum-spacetime-phenomenology review I shall only make use of one DSR argument, that applies
to cases in which indeed the dispersion relation is modified. This concerns the fact that in the presence of
observer-independent modifications of the dispersion relation (DSR-)relativistic invariance imposes the
presence of associated modifications of the law of energy-momentum conservation. More general discussions
of this issue are offered in Refs. [58 , 63
, 63 ], but it is here sufficient to illustrate it in a specific example. Let us
then consider a dispersion relation whose leading-order deformation (by a length scale
], but it is here sufficient to illustrate it in a specific example. Let us
then consider a dispersion relation whose leading-order deformation (by a length scale 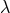 ) is given by
) is given by
 , 63
, 63 ]
]
The issue concerning energy-momentum conservation arises because both the dispersion relation and
the law of energy-momentum conservation must be (DSR-)relativistic. And the boosts (6 ),
which enforce relativistically the modification of the dispersion relation, are incompatible with
the standard form of energy-momentum conservation. For example, for processes with two
incoming particles,
),
which enforce relativistically the modification of the dispersion relation, are incompatible with
the standard form of energy-momentum conservation. For example, for processes with two
incoming particles,  and
and 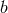 , and two outgoing particles,
, and two outgoing particles,  and
and 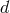 , the requirements
, the requirements
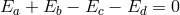 and
and 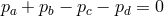 are not observer-independent laws according to (6
are not observer-independent laws according to (6 ).
An example of a modification of energy-momentum conservation that is compatible with (6
).
An example of a modification of energy-momentum conservation that is compatible with (6 ) is [58
) is [58 ]
]
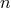 incoming particles and
incoming particles and  outgoing particles. In particular, in the case of a two-body particle decay
outgoing particles. In particular, in the case of a two-body particle decay 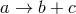 the laws
provide an acceptable (observer-independent, covariant according to (6
the laws
provide an acceptable (observer-independent, covariant according to (6 )) possibility.
)) possibility.
This observation provides a general motivation for contemplating modifications of the law of
energy-momentum conservation in frameworks with modified dispersion relations. And I shall often test the
potential impact on the phenomenology of introducing such modifications of the conservation of
energy-momentum by using as examples DSR-inspired laws of the type (7 ), (8
), (8 ), (9
), (9 ), (10
), (10 ). I shall do this
without necessarily advocating a DSR interpretation: knowing whether or not the outcome of tests of
modifications of the dispersion relation depends on the possibility of also having a modification of the
momentum-conservation laws is of intrinsic interest, with or without the DSR intuition. But I
must stress that when the relativistic symmetries are broken (rather than deformed in the DSR
sense) there is no a priori reason to modify the law of energy-momentum conservation, even
when the dispersion relation is modified. Indeed most authors adopting modified dispersion
relations within a broken-symmetry scenario keep the law of energy-momentum conservation
undeformed.
). I shall do this
without necessarily advocating a DSR interpretation: knowing whether or not the outcome of tests of
modifications of the dispersion relation depends on the possibility of also having a modification of the
momentum-conservation laws is of intrinsic interest, with or without the DSR intuition. But I
must stress that when the relativistic symmetries are broken (rather than deformed in the DSR
sense) there is no a priori reason to modify the law of energy-momentum conservation, even
when the dispersion relation is modified. Indeed most authors adopting modified dispersion
relations within a broken-symmetry scenario keep the law of energy-momentum conservation
undeformed.
On the other hand the DSR research program has still not reached the maturity for providing a fully satisfactory interpretation of the nonlinearities in the conservation laws. For some time the main challenge came (in addition to the mentioned interpretational challenges connected with spacetime locality) from arguments suggesting that one might well replace a given nonlinear setup for a DSR model with one obtained by redefining nonlinearly the coordinatization of momentum space (see, e.g., Ref. [26]). When contemplating such changes of coordinatization of momentum space many interpretational challenges appeared to arise. In my opinion, also in this direction the recent DSR literature has made significant progress, by casting the nonlinearities for momentum-space properties in terms of geometric entities, such as the metric and the affine connection on momentum space (see, e.g., Ref. [67]). This novel geometric interpretation is offering several opportunities for addressing the interpretational challenges, but the process is still far from complete.
3.2 Preliminaries on test theories with modified dispersion relation
So far the main focus of Poincaré-symmetry tests planned from a quantum-spacetime-phenomenology perspective has been on the form of the energy-momentum dispersion relation. Indeed, certain analyses of formalisms provide encouragement for the possibility that the Minkowski limit of quantum gravity might indeed be characterized by modified dispersion relations. However, the complexity of the formalisms that motivate the study of Planck-scale modifications of the dispersion relation is such that one has only partial information on the form of the correction terms and actually one does not even establish robustly the presence of modifications of the dispersion relation. Still, in some cases, most notably within some LQG studies and some studies of noncommutative spacetimes, the “theoretical evidence” in favor of modifications of the dispersion relations appears to be rather robust.
This is exactly the type of situation that I mentioned earlier in this review as part of a preliminary characterization of the peculiar type of test theories that must at present be used in quantum-spacetime phenomenology. It is not possible to compare to data the predictions for departures from Poincaré symmetry of LQG and/or noncommutative geometry because these theories do not yet provide a sufficiently rich description of the structures needed for actually doing phenomenology with modified dispersion relations. What we can compare to data are some simple models inspired by the little we believe we understand of the relevant issues within the theories that provide motivation for this phenomenology.
And the development of such models requires a delicate balancing act. If we only provide them with the structures we do understand of the original theories they will be as sterile as the original theories. So, we must add some structure, make some assumptions, but do so with prudence, limiting as much as possible the risk of assuming properties that could turn out not to be verified once we understand the relevant formalisms better.
As this description should suggest, there has been a proliferation of models adopted by different authors, each reflecting a different intuition on what could or could not be assumed. Correspondingly, in order to make a serious overall assessment of the experimental limits so far established with quantum-spacetime phenomenology of modified dispersion relations, one should consider a huge zoo of parameters. Even the parameters of the same parametrization of modifications of the dispersion relation when analyzed using different assumptions about other aspects of the model should really be treated as different/independent sets of parameters.
I shall be satisfied with considering some illustrative examples of models, chosen in such a way as to represent possibilities that are qualitatively very different, and representative of the breadth of possibilities that are under consideration. These examples of models will then be used in some relevant parts of this review as “language” for the description of the sensitivity to Planck-scale effects that is within the reach of certain experimental analyses.
3.2.1 With or without standard quantum field theory?
Before describing actual test theories, I should at least discuss the most significant among the issues that must be considered in setting up any such test theory with modified dispersion relation. This concerns the choice of whether or not to assume that the test theory should be a standard low-energy effective quantum field theory.
A significant portion of the quantum-gravity and quantum-spacetime community is rather skeptical of the results obtained using low-energy effective field theory in analyses relevant to the Planck-scale regime. One of the key reasons for this skepticism is the description given by effective field theory of the cosmological constant. The cosmological constant is the most significant experimental fact of evident gravitational relevance that could be within the reach of effective field theory. And current approaches to deriving the cosmological constant within effective field theory produce results, which are some 120 orders of magnitude greater than allowed by observations.15
However, just like there are several researchers who are skeptical about any results obtained using low-energy effective field theory in analyses relevant for the quantum-gravity/quantum-spacetime regime, there are also quite a few researchers who feel that it should be ok to assume a description in terms of effective field theory for all low-energy (sub-Planckian) manifestations of the quantum-gravity/quantum-spacetime regime.
Adopting a strict phenomenologist viewpoint, perhaps the most important observation is that for several
of the effects discussed in this section on UV corrections to Lorentz symmetry, and for some of the effects
discussed in later sections, studies based on effective quantum field theory can only be performed with a
rather strongly “pragmatic” attitude. One would like to confine the new effects to unexplored high-energy
regimes, by adjusting bare parameters accordingly, but, as I shall stress again later, quantum corrections
produce [455 , 182
, 182 , 515
, 515 , 190
, 190 ] effects that are nonetheless significant at accessible low energies,
unless one allows for rather severe fine-tuning. On the other hand, we do not have enough clues
concerning setups alternative to quantum-field theory that could be used. For example, as I
discuss in detail later, some attempts are centered on density-matrix formalisms that go beyond
quantum mechanics, but those are (however legitimate) mere speculations at the present time.
Nonetheless several of the phenomenologists involved, myself included, feel that in such a situation
phenomenology cannot be stopped by the theory impasse, even at the risk of later discovering
that the whole (or a sizable part of) the phenomenological effort was not on sound conceptual
bases.
] effects that are nonetheless significant at accessible low energies,
unless one allows for rather severe fine-tuning. On the other hand, we do not have enough clues
concerning setups alternative to quantum-field theory that could be used. For example, as I
discuss in detail later, some attempts are centered on density-matrix formalisms that go beyond
quantum mechanics, but those are (however legitimate) mere speculations at the present time.
Nonetheless several of the phenomenologists involved, myself included, feel that in such a situation
phenomenology cannot be stopped by the theory impasse, even at the risk of later discovering
that the whole (or a sizable part of) the phenomenological effort was not on sound conceptual
bases.
But I stress that even when contemplating the possibility of physics outside the domain of effective
quantum field theory, one inevitably must at least come to terms with the success of effective field
theory in reproducing a vast class of experimental data. In this respect, at least for studies of
Planck-scale departures from classical-spacetime relativistic symmetries I find particularly intriguing a
potential “order-of-limits issue”. The effective-field-theory description might be applicable only in
reference frames in which the process of interest is essentially occurring in its center of mass (no
“Planck-large boost” [60] with respect to the center-of-mass frame). The field theoretic description
could emerge in a sort of “low-boost limit”, rather than the expected low-energy limit. The
regime of low boosts with respect to the center-of-mass frame is often indistinguishable from the
low-energy limit. For example, from a Planck-scale perspective, our laboratory experiments
(even the ones conducted at, e.g., CERN, DESY, SLAC, …) are both low boost (with respect
to the center-of-mass frame) and low energy. However, some contexts that are of interest in
quantum-gravity phenomenology, such as the collisions between ultra-high-energy cosmic-ray protons and
CMBR photons, are situations where all the energies of the particles are still tiny with respect
to the Planck energy scale, but the boost with respect to the center-of-mass frame could be
considered to be “large” from a Planck-scale perspective: the Lorentz factor 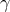 with respect to the
proton rest frame is much greater than the ratio between the Planck scale and the proton mass
with respect to the
proton rest frame is much greater than the ratio between the Planck scale and the proton mass
Another interesting scenario concerning the nature of the limit through which quantum-spacetime physics should reproduce ordinary physics is suggested by results on field theories in noncommutative spacetimes. One can observe that a spacetime characterized by an uncertainty relation of the type
never really behaves as a classical spacetime, not even at very low energies. In fact, according to this type of uncertainty relation, a low-energy process involving soft momentum exchange in the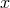 direction (large
direction (large
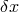 ) should somehow be connected to the exchange of a hard momentum in the
) should somehow be connected to the exchange of a hard momentum in the 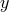 direction
(
direction
(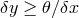 ), and this feature cannot faithfully be captured by our ordinary field-theory formalisms. For
the “canonical noncommutative spacetimes” one does obtain a plausible-looking field theory [213
), and this feature cannot faithfully be captured by our ordinary field-theory formalisms. For
the “canonical noncommutative spacetimes” one does obtain a plausible-looking field theory [213 ], but the
results actually show that it is not possible to rely on an ordinary effective low-energy quantum-field-theory
description because of the presence of “UV/IR mixing”[213
], but the
results actually show that it is not possible to rely on an ordinary effective low-energy quantum-field-theory
description because of the presence of “UV/IR mixing”[213 , 397
, 397 ] (a mechanism such that the high-energy
sector of the theory does not decouple from the low-energy sector, which in turn very severely
affects the prospects of analyses based on an ordinary effective low-energy quantum-field-theory
description). For other (non-canonical) noncommutative spacetimes we are still struggling in
the search for a satisfactory formulation of a quantum field theory [335, 64], and it is at this
point legitimate to worry that such a formulation of dynamics in those spacetimes does not
exist.
] (a mechanism such that the high-energy
sector of the theory does not decouple from the low-energy sector, which in turn very severely
affects the prospects of analyses based on an ordinary effective low-energy quantum-field-theory
description). For other (non-canonical) noncommutative spacetimes we are still struggling in
the search for a satisfactory formulation of a quantum field theory [335, 64], and it is at this
point legitimate to worry that such a formulation of dynamics in those spacetimes does not
exist.
And the assumption of availability of an ordinary effective low-energy quantum-field-theory description has also been challenged by some perspectives on the LQG approach. For example, the arguments presented in Ref. [245] suggest that in several contexts in which one would naively expect a low-energy field theory description LQG might instead require a density-matrix description with features going beyond the reach of effective quantum field theory.
3.2.2 Other key features of test theories with modified dispersion relation
In order to be applicable to a significant ensemble of experimental contexts, a test theory should specify much more than the form of the dispersion relation. In light of the type of data that we expect to have access to (see later, e.g., Sections 3.4, 3.5, and 3.8), besides the choice of working within or without low-energy effective quantum field theory, there are at least three other issues that the formulation of such a test theory should clearly address:
-
(i) is the modification of the dispersion relation “universal”? or should one instead allow different modification parameters for different particles?
-
(ii) in the presence of a modified dispersion relation between the energy
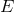 and the momentum
and the momentum
 of a particle, should we still assume the validity of the relation
of a particle, should we still assume the validity of the relation 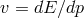 between the
speed of a particle and its dispersion relation?
between the
speed of a particle and its dispersion relation?
-
(iii) in the presence of a modified dispersion relation, should we still assume the validity of the standard law of energy-momentum conservation?
Unfortunately on these three key points, the quantum-spacetime pictures that are providing motivation for the study of Planck-scale modifications of the dispersion relation are not giving us much guidance yet.
For example, in LQG, while we do have some (however fragile and indirect) evidence that the dispersion
relation should be modified, we do not yet have a clear indication concerning whether the law of
energy-momentum conservation should also be modified and we also cannot yet establish whether the
relation 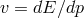 should be preserved.
should be preserved.
Similarly, in the analysis of noncommutative spacetimes we are close to establishing rather robustly the
presence of modifications of the dispersion relation, but other aspects of the relevant theories have
not yet been clarified. While most of the literature for canonical noncommutative spacetimes
assumes [213 , 397
, 397 ] that the law of energy-momentum conservation should not be modified, most
of the literature on
] that the law of energy-momentum conservation should not be modified, most
of the literature on  -Minkowski spacetime argues in favor of a modification of the law of
energy-momentum conservation. There is also still no consensus on the relation between speed
and dispersion, and particularly in the
-Minkowski spacetime argues in favor of a modification of the law of
energy-momentum conservation. There is also still no consensus on the relation between speed
and dispersion, and particularly in the  -Minkowski literature some departures from the
-Minkowski literature some departures from the
 relation are actively considered [336, 414, 199, 351]. And at least for canonical
noncommutative spacetimes the possibility of a nonuniversal dispersion relation is considered
extensively [213
relation are actively considered [336, 414, 199, 351]. And at least for canonical
noncommutative spacetimes the possibility of a nonuniversal dispersion relation is considered
extensively [213 , 397
, 397 ].
].
Concerning the relation 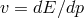 it may be useful to stress that it can be obtained assuming that a
Hamiltonian description is still available,
it may be useful to stress that it can be obtained assuming that a
Hamiltonian description is still available, ![v = dx ∕dt ∼ [x, H (p )]](article151x.gif) , and that the Heisenberg uncertainty
principle still holds exactly (
, and that the Heisenberg uncertainty
principle still holds exactly (![[x,p] = 1 → x ∼ ∂∕∂p](article152x.gif) ). The possibility of modifications of the Hamiltonian
description is an aspect of the debate on “Planck-scale dynamics” that was in part discussed in
Section 3.2.1. And concerning the Heisenberg uncertainty principle I have already mentioned some
arguments that invite us to contemplate modifications.
). The possibility of modifications of the Hamiltonian
description is an aspect of the debate on “Planck-scale dynamics” that was in part discussed in
Section 3.2.1. And concerning the Heisenberg uncertainty principle I have already mentioned some
arguments that invite us to contemplate modifications.
3.2.3 A test theory for pure kinematics
With so many possible alternative ingredients to mix one can of produce a large variety of test theories. As mentioned, I intend to focus on some illustrative examples of test theories for my characterization of achievable experimental sensitivities.
My first example is a test theory of very limited scope, since it is conceived to only describe pure-kinematics effects. This will strongly restrict the class of experiments that can be analyzed in terms of this test theory, but the advantage is that the limits obtained on the parameters of this test theory will have rather wide applicability (they will apply to any quantum-spacetime theory with that form of kinematics, independent of the description of dynamics).
The first element of this test theory, introduced from a quantum-spacetime-phenomenology
perspective in Refs. [66 , 65
, 65 ], is a “universal” (same for all particles) dispersion relation of the form
], is a “universal” (same for all particles) dispersion relation of the form
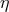 of order 1 and integer
of order 1 and integer 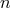 (
( ). This formula is compatible with some of the results
obtained in the LQG approach and reflects some results obtained for theories in
). This formula is compatible with some of the results
obtained in the LQG approach and reflects some results obtained for theories in  -Minkowski
noncommutative spacetime.
-Minkowski
noncommutative spacetime.
Already in the first studies [66 ] that proposed a phenomenology based on (13
] that proposed a phenomenology based on (13 ) it was assumed that even
at the Planck scale the familiar description of “group velocity”, obtained from the dispersion relation
according to
) it was assumed that even
at the Planck scale the familiar description of “group velocity”, obtained from the dispersion relation
according to 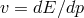 , would hold.
, would hold.
And in other early phenomenology works [327 , 38
, 38 , 73
, 73 , 463
, 463 ] based on (13
] based on (13 ) it was assumed that the law
of energy-momentum conservation should not be modified at the Planck scale, so that, for example, in a
) it was assumed that the law
of energy-momentum conservation should not be modified at the Planck scale, so that, for example, in a
 particle-physics process one would have
particle-physics process one would have
In the following, I will refer to this test theory as the “PKV0 test theory”, where “PK” reflects its
“Pure-Kinematics” nature, “V” reflects its “Lorentz-symmetry Violation” content, and “0” reflects the fact
that it combines the dispersion relation (13 ) with what appears to be the most elementary set of
assumptions concerning other key aspects of the physics: universality of the dispersion relation,
) with what appears to be the most elementary set of
assumptions concerning other key aspects of the physics: universality of the dispersion relation,
 , and the unmodified law of energy-momentum conservation.
, and the unmodified law of energy-momentum conservation.
This rudimentary framework is a good starting point for exploring the relevant phenomenology. But one should also consider some of the possible variants. For example, the undeformed conservation of energy-momentum is relativistically incompatible with the deformation of the dispersion relation (so, in particular, the PKV0 test theory requires a preferred frame). Modifications of the law of energy-momentum conservation would be required in a DSR picture, and may be considered even in other scenarios.16
Evidently, the universality of the effect can and should be challenged. And there are indeed (as I shall
stress again later in this review) several proposals of test theories with different magnitudes of the effects for
different particles [395 , 308
, 308 ]. Let me just mention, in closing this section, a case that is particularly
challenging for phenomenology: the case of the variant of the PKV0 test theory allowing for
nonuniversality such that the effects are restricted only to photons [227, 74
]. Let me just mention, in closing this section, a case that is particularly
challenging for phenomenology: the case of the variant of the PKV0 test theory allowing for
nonuniversality such that the effects are restricted only to photons [227, 74 ], thereby limiting
significantly the class of observations/experiments that could test the scenario (see, however,
Ref. [380]).
], thereby limiting
significantly the class of observations/experiments that could test the scenario (see, however,
Ref. [380]).
3.2.4 A test theory based on low-energy effective field theory
The restriction to pure kinematics has the merit to allow us to establish constraints that are applicable to a relatively large class of quantum-spacetime scenarios (different formulations of dynamics would still be subject to the relevant constraints), but it also severely restricts the type of experimental contexts that can be considered, since it is only in rare instances (and only to some extent) that one can qualify an analysis as purely kinematical. Therefore, the desire to be able to analyze a wider class of experimental contexts is, therefore, providing motivation for the development of test theories more ambitious than the PKV0 test theory, with at least some elements of dynamics. This is rather reasonable, as long as one proceeds with awareness of the fact that, in light of the situation on the theory side, for test theories adopting a given description of dynamics there is a risk that we may eventually find out that none of the quantum-gravity approaches that are being pursued are reflected in the test theory.
When planning to devise a test theory that includes the possibility to describe dynamics,
the first natural candidate (not withstanding the concerns reviewed in Section 3.2.1) is the
framework of low-energy effective quantum field theory. In this section I want to discuss
a test theory that is indeed based on low-energy effective field theory, and has emerged
primarily17
from the analysis reported by Myers and Pospelov in Ref. [426 ]. Motivated mainly by the perspective of
LQG advocated in Ref. [247
]. Motivated mainly by the perspective of
LQG advocated in Ref. [247 ], this test theory explores the possibility of a linear-in-
], this test theory explores the possibility of a linear-in-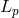 modification of the
dispersion relation
modification of the
dispersion relation
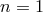 of Eq. (13
of Eq. (13 ). Perhaps the most notable outcome of the exercise of introducing such a
dispersion relation within an effective low-energy field-theory setup is the observation [426] that for the case
of electromagnetic radiation, assuming essentially only that the effects are characterized mainly by an
external four-vector, one arrives at a single possible correction term for the Lagrangian density:
where the four-vector
). Perhaps the most notable outcome of the exercise of introducing such a
dispersion relation within an effective low-energy field-theory setup is the observation [426] that for the case
of electromagnetic radiation, assuming essentially only that the effects are characterized mainly by an
external four-vector, one arrives at a single possible correction term for the Lagrangian density:
where the four-vector 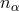 parameterizes the effect.
parameterizes the effect.
This is also a framework for broken Lorentz symmetry, since the (dimensionless) components of 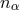 take different values in different reference frames, transforming as the components of a four-vector. And a
full-scope phenomenology for this proposal should explore [271] the four-dimensional parameter space,
take different values in different reference frames, transforming as the components of a four-vector. And a
full-scope phenomenology for this proposal should explore [271] the four-dimensional parameter space,
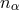 , taking into account the characteristic frame dependence of the parameters
, taking into account the characteristic frame dependence of the parameters 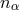 . As I discuss in later
parts of this section, there is already a rather sizable literature on this phenomenology, but still mainly
focused on what turns out to be the simplest possibility for the Myers–Pospelov framework, which relies
on the assumption that one is in a reference frame where
. As I discuss in later
parts of this section, there is already a rather sizable literature on this phenomenology, but still mainly
focused on what turns out to be the simplest possibility for the Myers–Pospelov framework, which relies
on the assumption that one is in a reference frame where 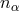 only has a time component,
only has a time component,
 . Then, upon introducing the convenient notation
. Then, upon introducing the convenient notation 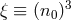 , one can rewrite (17
, one can rewrite (17 ) as
) as
 , then necessarily left-circular polarized photons satisfy the “opposite
sign” dispersion relation
, then necessarily left-circular polarized photons satisfy the “opposite
sign” dispersion relation 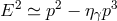 .
.
In the same spirit one can add spin-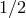 particles to the model, but for them the structure of the
framework does not introduce constraints on the parameters, and in particular there can be two
independent parameters
particles to the model, but for them the structure of the
framework does not introduce constraints on the parameters, and in particular there can be two
independent parameters 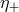 and
and 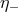 to characterize the modification of the dispersion relation for
fermions of different helicity:
to characterize the modification of the dispersion relation for
fermions of different helicity:
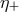 and
and 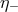 with respect to electrons). And there is no constraint on the relation
between
with respect to electrons). And there is no constraint on the relation
between  and
and 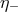 , but the consistency of the framework requires [308
, but the consistency of the framework requires [308 ] that for particle-antiparticle
pairs, the deformation should have opposite signs on opposite helicities, so that, for example,
] that for particle-antiparticle
pairs, the deformation should have opposite signs on opposite helicities, so that, for example,
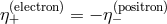 and
and 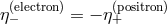 .
.
In some investigations one might prefer to look at particularly meaningful portions of this large parameter
space. For example, one might consider [62 ] the possibility that the deformation for all spin-
] the possibility that the deformation for all spin- particles
be characterized by only two parameters, the same two parameters for all particle-antiparticle pairs (leaving
open, however, some possible sign ambiguities to accommodate the possibility to choose between,
for example,
particles
be characterized by only two parameters, the same two parameters for all particle-antiparticle pairs (leaving
open, however, some possible sign ambiguities to accommodate the possibility to choose between,
for example,  and
and  ). In the
following I will refer to this test theory as the “FTV0 test theory”, where “FT” reflects its
adoption of a “low-energy effective Field Theory” description, “V” reflects its “Lorentz-symmetry
Violation” content, and “0” reflects the “minimalistic” assumption of “universality for spin-
). In the
following I will refer to this test theory as the “FTV0 test theory”, where “FT” reflects its
adoption of a “low-energy effective Field Theory” description, “V” reflects its “Lorentz-symmetry
Violation” content, and “0” reflects the “minimalistic” assumption of “universality for spin-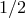 particles”.
particles”.
3.2.5 More on “pure-kinematics” and “field-theory-based” phenomenology
Before starting my characterization of experimental sensitivities in terms of the parameters of some test theories I find it appropriate to add a few remarks warning about some difficulties that are inevitably encountered.
For the pure-kinematics test theories, some key difficulties originate from the fact that sometimes an effect due to the modification of dynamics can take a form that is not easily distinguished from a pure-kinematics effect. And other times one deals with an analysis of effects that appear to be exclusively sensitive to kinematics but then at the stage of converting experimental results into bounds on parameters some level of dependence on dynamics arises. An example of this latter possibility will be provided by my description of particle-decay thresholds in test theories that violate Lorentz symmetry. The derivation of the equations that characterize the threshold requires only the knowledge of the laws of kinematics. And if, according to the kinematics of a given test theory, a certain particle at a certain energy cannot decay, then observation of the decay allows one to set robust pure-kinematics limits on the parameters. But if the test theory predicts that a certain particle at a certain energy can decay then by not finding such decays we are not in a position to truly establish pure-kinematics limits on the parameters of the test theory. If the decay is kinematically allowed but not seen, it is possible that the laws of dynamics prevent it from occurring (small decay amplitude).
By adopting a low-energy quantum field theory this type of limitations is removed, but other issues must be taken into account, particularly in association with the fact that the FTV0 quantum field theory is not renormalizable. Quantum-field-theory-based descriptions of Planck-scale departures from Lorentz symmetry can only be developed with a rather strongly “pragmatic” attitude. In particular, for the FTV0 test theory, with its Planck-scale suppressed effects at tree level, some authors (notably Refs. [455, 182, 515, 190]) have argued that the loop expansion could effectively generate additional terms of modification of the dispersion relation that are unsuppressed by the cut-off scale of the (nonrenormalizable) field theory. The parameters of the field theory can be fine-tuned to eliminate unwanted large effects, but the needed level of fine tuning is usually rather unpleasant. While certainly undesirable, this severe fine-tuning problem should not discourage us from considering the FTV0 test theory, at least not at this early stage of the development of the relevant phenomenology. Actually some of the most successful theories used in fundamental physics are affected by severe fine tuning. It is not uncommon to eventually discover that the fine tuning is only apparent, and some hidden symmetry is actually “naturally” setting up the hierarchy of parameters.
In particular, it is already established that supersymmetry can tame the fine-tuning issue [268 , 130
, 130 ]. If
one extends supersymmetric quantum electrodynamics by adding interactions with external vector and
tensor backgrounds that violate Lorentz symmetry at the Planck scale, then exact supersymmetry
requires that such interactions correspond to operators of dimension five or higher, so that no
fine-tuning is needed in order to suppress the unwanted operators of dimension lower than five.
Supersymmetry can only be an approximate symmetry of the physical world, and the effects of the
scale of soft-supersymmetry-breaking masses controls the renormalization-group evolution of
dimension five Lorentz-violating operators and their mixing with dimension three Lorentz-violating
operators [268, 130].
]. If
one extends supersymmetric quantum electrodynamics by adding interactions with external vector and
tensor backgrounds that violate Lorentz symmetry at the Planck scale, then exact supersymmetry
requires that such interactions correspond to operators of dimension five or higher, so that no
fine-tuning is needed in order to suppress the unwanted operators of dimension lower than five.
Supersymmetry can only be an approximate symmetry of the physical world, and the effects of the
scale of soft-supersymmetry-breaking masses controls the renormalization-group evolution of
dimension five Lorentz-violating operators and their mixing with dimension three Lorentz-violating
operators [268, 130].
It has also been established [461] that if Lorentz violation occurs in the gravitational sector, then the violations of Lorentz symmetry induced on the matter sector do not require severe fine-tuning. In particular, this has been investigated by coupling the Standard Model of particle physics to a Hořava–Lifshitz description of gravitational phenomena.
The study of Planck-scale departures from Lorentz symmetry may find some encouragement in perspectives based on renormalization theory, at least in as much as it has been shown [79, 78, 289, 507] that some field theories modified by Lorentz-violating terms are actually rather well behaved in the UV.
3.3 Photon stability
3.3.1 Photon stability and modified dispersion relations
The first example of Planck-scale sensitivity that I discuss is the case of a process that is kinematically
forbidden in the presence of exact Lorentz symmetry, but becomes kinematically allowed in
the presence of certain departures from Lorentz symmetry. It has been established (see, e.g.,
Refs. [305 , 59
, 59 , 334
, 334 , 115
, 115 ]) that when Lorentz symmetry is broken at the Planck scale, there can be
significant implications for certain decay processes. At the qualitative level, the most significant
novelty would be the possibility for massless particles to decay. And certain observations in
astrophysics, which allow us to establish that photons of energies up to
]) that when Lorentz symmetry is broken at the Planck scale, there can be
significant implications for certain decay processes. At the qualitative level, the most significant
novelty would be the possibility for massless particles to decay. And certain observations in
astrophysics, which allow us to establish that photons of energies up to 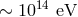 are stable,
can then be used [305
are stable,
can then be used [305 , 59
, 59 , 334, 115
, 334, 115 ] to set limits on schemes for departures from Lorentz
symmetry.
] to set limits on schemes for departures from Lorentz
symmetry.
For my purposes it suffices to consider the process 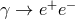 . Let us start from the perspective of the
PKV0 test theory, and therefore adopt the dispersion relation (13
. Let us start from the perspective of the
PKV0 test theory, and therefore adopt the dispersion relation (13 ) and unmodified energy-momentum
conservation. One easily finds a relation between the energy
) and unmodified energy-momentum
conservation. One easily finds a relation between the energy 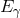 of the incoming photon, the opening
angle
of the incoming photon, the opening
angle 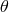 between the outgoing electron-positron pair, and the energy
between the outgoing electron-positron pair, and the energy  of the outgoing positron (the
energy of the outgoing electron is simply given by
of the outgoing positron (the
energy of the outgoing electron is simply given by  ). Setting
). Setting 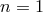 in (13
in (13 ) one
finds that, for the region of phase space with
) one
finds that, for the region of phase space with  , this relation takes the form
, this relation takes the form
 is the electron mass.
is the electron mass.
The fact that for 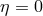 Eq. (21
Eq. (21 ) would require
) would require 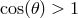 reflects the fact that, if Lorentz symmetry
is preserved, the process
reflects the fact that, if Lorentz symmetry
is preserved, the process 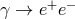 is kinematically forbidden. For
is kinematically forbidden. For 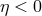 the process is still forbidden,
but for positive
the process is still forbidden,
but for positive 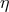 high-energy photons can decay into an electron-positron pair. In fact, for
high-energy photons can decay into an electron-positron pair. In fact, for
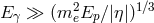 one finds that there is a region of phase space where
one finds that there is a region of phase space where  , i.e., there is a
physical phase space available for the decay.
, i.e., there is a
physical phase space available for the decay.
The energy scale 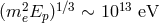 is not too high for testing, since, as mentioned, in astrophysics
we see photons of energies up to
is not too high for testing, since, as mentioned, in astrophysics
we see photons of energies up to 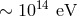 that are stable (they clearly travel safely some large
astrophysical distances). The level of sensitivity that is within reach of these studies therefore goes at least
down to values of (positive)
that are stable (they clearly travel safely some large
astrophysical distances). The level of sensitivity that is within reach of these studies therefore goes at least
down to values of (positive) 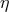 of order 1 and somewhat smaller than 1. This is what one describes as
“Planck-scale sensitivity” in the quantum-spacetime phenomenology literature: having set the
dimensionful deformation parameter to the Planck-scale value, the coefficient of the term that
can be tested is of order 1 or smaller. However, specifically for the case of the photon-stability
analysis it is rather challenging to transform this Planck-scale sensitivity into actual experimental
limits.
of order 1 and somewhat smaller than 1. This is what one describes as
“Planck-scale sensitivity” in the quantum-spacetime phenomenology literature: having set the
dimensionful deformation parameter to the Planck-scale value, the coefficient of the term that
can be tested is of order 1 or smaller. However, specifically for the case of the photon-stability
analysis it is rather challenging to transform this Planck-scale sensitivity into actual experimental
limits.
Within PKV0 kinematics, for 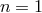 and positive
and positive  of order 1, it would have been natural to expect
that photons with
of order 1, it would have been natural to expect
that photons with 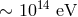 energy are unstable. But the fact that the decay of
energy are unstable. But the fact that the decay of  photons is
allowed by PKV0 kinematics of does not guarantee that these photons should rapidly decay. It depends on
the relevant probability amplitude, whose evaluation goes beyond the reach of kinematics. Still, it is
likely that these observations are very significant for theories that are compatible with PKV0
kinematics. For a theory that is compatible with PKV0 kinematics (with positive
photons is
allowed by PKV0 kinematics of does not guarantee that these photons should rapidly decay. It depends on
the relevant probability amplitude, whose evaluation goes beyond the reach of kinematics. Still, it is
likely that these observations are very significant for theories that are compatible with PKV0
kinematics. For a theory that is compatible with PKV0 kinematics (with positive 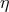 ) this evidence
of stability of photons imposes the identification of a dynamical mechanism that essentially
prevents photon decay. If one finds no such mechanism, the theory is “ruled out” (or at least
its parameters are severely constrained), but in principle one could look endlessy for such a
mechanism. A balanced approach to this issue must take into account that quantum-spacetime
physics may well modify both kinematics and the strength (and nature) of interactions at a
certain scale, and it might in principle do this in ways that cannot be accommodated within the
confines of effective quantum field theory, but one should take notice of the fact that, even in
some new (to-be-discovered) framework outside effective quantum field theory, it is unlikely
that there will be very large “conspiracies” between the modifications of kinematics and the
modifications of the strength of interaction. In principle, models based on pure kinematics are
immune from certain bounds on parameters that are also derived also using descriptions of
the interactions, and it is conceivable that in the correct theory the actual bound would be
somewhat shifted from the value derived within effective quantum field theory. But in order
to contemplate large differences in the bounds one would need to advocate very large and ad
hoc modifications of the strength of interactions, large enough to compensate for the often
dramatic implications of the modifications of kinematics. The challenge then is to find satisfactory
criteria for confining speculations about variations of the strengths of interaction only within a
certain plausible range. To my knowledge this has not yet been attempted, but it deserves high
priority.
) this evidence
of stability of photons imposes the identification of a dynamical mechanism that essentially
prevents photon decay. If one finds no such mechanism, the theory is “ruled out” (or at least
its parameters are severely constrained), but in principle one could look endlessy for such a
mechanism. A balanced approach to this issue must take into account that quantum-spacetime
physics may well modify both kinematics and the strength (and nature) of interactions at a
certain scale, and it might in principle do this in ways that cannot be accommodated within the
confines of effective quantum field theory, but one should take notice of the fact that, even in
some new (to-be-discovered) framework outside effective quantum field theory, it is unlikely
that there will be very large “conspiracies” between the modifications of kinematics and the
modifications of the strength of interaction. In principle, models based on pure kinematics are
immune from certain bounds on parameters that are also derived also using descriptions of
the interactions, and it is conceivable that in the correct theory the actual bound would be
somewhat shifted from the value derived within effective quantum field theory. But in order
to contemplate large differences in the bounds one would need to advocate very large and ad
hoc modifications of the strength of interactions, large enough to compensate for the often
dramatic implications of the modifications of kinematics. The challenge then is to find satisfactory
criteria for confining speculations about variations of the strengths of interaction only within a
certain plausible range. To my knowledge this has not yet been attempted, but it deserves high
priority.
A completely analogous calculation can be done within the FTV0 test theory, and there one can easily
arrive at the conclusion[377] that the FTV0 description of dynamics should not significantly suppress the
photon-decay process. However, as mentioned, consistency with the effective-field-theory setup requires that
the two polarizations of the photon acquire opposite-sign modifications of the dispersion relation. We
observe in astrophysics some photons of energies up to 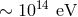 that are stable over large distances, but
as far as we know those photons could be all right-circular polarized (or all left-circular polarized). This
evidence of stability of photons, therefore, is only applicable to the portion of the FTV0 parameter space in
which both polarizations should be unstable (a subset of the region with
that are stable over large distances, but
as far as we know those photons could be all right-circular polarized (or all left-circular polarized). This
evidence of stability of photons, therefore, is only applicable to the portion of the FTV0 parameter space in
which both polarizations should be unstable (a subset of the region with  and
and
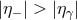 ).
).
3.3.2 Photon stability and modified energy-momentum conservation
So far I have discussed photon stability assuming that only the dispersion relation is modified. If the
modification of the dispersion relation is instead combined with a modification of the law of
energy-momentum conservation the results can change very significantly. In order to expose these changes in
rather striking fashion let me consider the example of DSR-inspired laws of energy-momentum conservation
for the case of 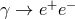 :
:
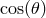 that is still of the form
that is still of the form 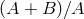 but now with
but now with 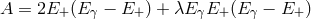 and
and
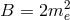 :
Evidently, this formula always gives
:
Evidently, this formula always gives 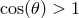 , so there are combinations of modifications of the
dispersion relation and modifications of energy-momentum conservation such that
, so there are combinations of modifications of the
dispersion relation and modifications of energy-momentum conservation such that  is still
forbidden.
is still
forbidden.
If the modification of the dispersion relation and the modification of the law of energy-momentum conservation are not matched exactly to get this result, then one can have the possibility of photon decay, but in some cases it can be further suppressed (in addition to the Planck-scale suppression) by the partial compensation between the two modifications.
The fact that the matching between modification of the dispersion relation and modification of
the law of energy-momentum conservation that produces a stable photon is obtained using
a DSR-inspired setup is not surprising [63 ]. The relativistic properties of the framework are
clearly at stake in this derivation. A threshold-energy requirement for particle decay (such as the
]. The relativistic properties of the framework are
clearly at stake in this derivation. A threshold-energy requirement for particle decay (such as the
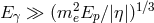 mentioned above) cannot be introduced as an observer-independent law,
and is therefore incompatible with any relativistic (even DSR-relativistic) formulation of the
laws of physics. In fact, different observers assign different values to the energy of a particle
and, therefore, in the presence of a threshold-energy requirement for particle decay a given
particle should be allowed to decay, according to some observers while being totally stable for
others.
mentioned above) cannot be introduced as an observer-independent law,
and is therefore incompatible with any relativistic (even DSR-relativistic) formulation of the
laws of physics. In fact, different observers assign different values to the energy of a particle
and, therefore, in the presence of a threshold-energy requirement for particle decay a given
particle should be allowed to decay, according to some observers while being totally stable for
others.
3.4 Pair-production threshold anomalies and gamma-ray observations
Another opportunity to investigate quantum-spacetime-inspired Planck-scale departures from
Lorentz symmetry is provided by certain types of energy thresholds for particle-production
processes that are relevant in astrophysics. This is a very powerful tool for quantum-spacetime
phenomenology [327 , 38
, 38 , 73
, 73 , 463
, 463 , 512, 364, 307, 494], and, in fact, at the beginning of this review, I
chose the evaluation of the threshold energy for photopion production,
, 512, 364, 307, 494], and, in fact, at the beginning of this review, I
chose the evaluation of the threshold energy for photopion production, 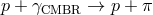 , as the basis
for illustrating how the sensitivity levels that are within our reach can be placed in rather natural
connection with effects introduced at the Planck scale.
, as the basis
for illustrating how the sensitivity levels that are within our reach can be placed in rather natural
connection with effects introduced at the Planck scale.
I discuss the photopion production threshold analysis in more detail in Section 3.5. Here, I consider
instead the electron-positron pair production process, 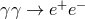 .
.
3.4.1 Modified dispersion relations and 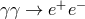
The threshold for 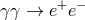 is relevant for studies of the opacity of our Universe to photons. In
particular, according to the conventional (classical-spacetime) description, the IR diffuse extragalactic
background should give rise to the strong absorption of “TeV photons” (here understood as photons with
energy
is relevant for studies of the opacity of our Universe to photons. In
particular, according to the conventional (classical-spacetime) description, the IR diffuse extragalactic
background should give rise to the strong absorption of “TeV photons” (here understood as photons with
energy  ), but this prediction must be reassessed in the presence of violations of
Lorentz symmetry.
), but this prediction must be reassessed in the presence of violations of
Lorentz symmetry.
To show that this is the case, let me start once again from the perspective of the PKV0 test theory, and
analyze a collision between a soft photon of energy  and a high-energy photon of energy
and a high-energy photon of energy 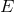 , which
might produce an electron-positron pair. Using the dispersion relation (13
, which
might produce an electron-positron pair. Using the dispersion relation (13 ) (for
) (for 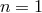 ) and the
(unmodified) law of energy-momentum conservation, one finds that for given soft-photon energy
) and the
(unmodified) law of energy-momentum conservation, one finds that for given soft-photon energy  , the
process
, the
process  is allowed only if
is allowed only if 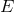 is greater than a certain threshold energy
is greater than a certain threshold energy 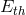 that
depends on
that
depends on  and
and 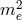 , as implicitly codified in the formula (valid for
, as implicitly codified in the formula (valid for 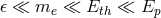 )
)
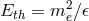 corresponds to the
corresponds to the 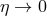 limit of (25
limit of (25 ). For
). For 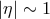 the
Planck-scale correction can be safely neglected as long as
the
Planck-scale correction can be safely neglected as long as  . But eventually, for sufficiently
small values of
. But eventually, for sufficiently
small values of  (and correspondingly large values of
(and correspondingly large values of  ) the Planck-scale correction cannot be
ignored.
) the Planck-scale correction cannot be
ignored.
This provides an opportunity for a pure-kinematics test: if a 10 TeV photon collides with a photon of
0.03 eV and produces an electron-positron pair the case 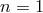 ,
, 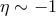 for the PKV0 test theory is
ruled out. A 10 TeV photon and a 0.03 eV photon can produce an electron-positron pair according to
ordinary special-relativistic kinematics (and its associated requirement
for the PKV0 test theory is
ruled out. A 10 TeV photon and a 0.03 eV photon can produce an electron-positron pair according to
ordinary special-relativistic kinematics (and its associated requirement 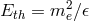 ), but they
cannot produce an electron-positron pair according to PKV0 kinematics with
), but they
cannot produce an electron-positron pair according to PKV0 kinematics with 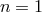 and
and
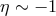 .
.
For positive 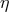 the situation is somewhat different. While negative
the situation is somewhat different. While negative 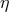 increases the energy
requirement for electron-positron pair production, positive
increases the energy
requirement for electron-positron pair production, positive 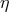 decreases the energy requirement for
electron-positron pair production. In some cases, where one would expect electron-positron pair production
to be forbidden, the PKV0 test theory with positive
decreases the energy requirement for
electron-positron pair production. In some cases, where one would expect electron-positron pair production
to be forbidden, the PKV0 test theory with positive 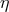 would instead allow it. But once a process is
allowed there is no guarantee that it will actually occur, not without some information on the
description of dynamics (that allows us to evaluate cross sections). As in the case of photon decay,
one must conclude that a pure-kinematics framework can be falsified when it predicts that a
process cannot occur (if instead the process is seen) but in principle it cannot be falsified when it
predicts that a process is allowed. Here too, one should gradually develop balanced criteria
taking into account the remarks I offer in Section 3.3.1 concerning the plausibility (or lack
thereof) of conspiracies between modifications of kinematics and modifications of the strengths of
interaction.
would instead allow it. But once a process is
allowed there is no guarantee that it will actually occur, not without some information on the
description of dynamics (that allows us to evaluate cross sections). As in the case of photon decay,
one must conclude that a pure-kinematics framework can be falsified when it predicts that a
process cannot occur (if instead the process is seen) but in principle it cannot be falsified when it
predicts that a process is allowed. Here too, one should gradually develop balanced criteria
taking into account the remarks I offer in Section 3.3.1 concerning the plausibility (or lack
thereof) of conspiracies between modifications of kinematics and modifications of the strengths of
interaction.
Concerning the level of sensitivity that we can expect to achieve in this case one can robustly claim that Planck-scale sensitivity is within our reach. This, as anticipated above, is best seen considering the “TeV photons” emitted by some blazars, for which (as they travel toward our Earth detectors) the photons of the IR diffuse extragalactic background are potential targets for electron-positron pair production. In estimating the sensitivity achievable with this type of analyses it is necessary to take into account the fact that, besides the form of the threshold condition, there are at least three other factors that play a role in establishing the level of absorption of TeV photons emitted by a given blazar: our knowledge of the type of signal emitted by the blazar (at the source), the distance of the blazar, and most importantly the density of the IR diffuse extragalactic background.
The availability of observations of the relevant type has increased very significantly over these past few
years. For example, for the blazar “Markarian 501” (at a redshift of  ) and the blazar
“H1426+428” (at a redshift of
) and the blazar
“H1426+428” (at a redshift of 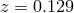 ) robust observations up to the 20-TeV range have been
reported [15
) robust observations up to the 20-TeV range have been
reported [15 , 16
, 16 ], and for the blazar “Markarian 421” (at a redshift of
], and for the blazar “Markarian 421” (at a redshift of 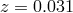 ) observations of
photons of energy up to 45 TeV has been reported [438
) observations of
photons of energy up to 45 TeV has been reported [438 ], although a more robust signal is seen once again
up to the 20-TeV range [355
], although a more robust signal is seen once again
up to the 20-TeV range [355 , 17
, 17 ].
].
The key obstruction for translating these observations into an estimate of the effectiveness of
pair-production absorption comes from the fact that measurements of the density of the IR diffuse
extragalactic background are very difficult, and as a result our experimental information on this density is
still affected by large uncertainties [235, 536 , 111
, 111 , 278].
, 278].
The observations do show convincingly that some absorption is occurring [15 , 16
, 16 , 438, 355
, 438, 355 , 17
, 17 ]. I
should stress the fact that the analysis of the combined X-ray/TeV-gamma-ray spectrum for the Markarian
421 blazar, as discussed in Ref. [333], provides rather compelling evidence. The X-ray part of the spectrum
allows one to predict the TeV-gamma-ray part of the spectrum in a way that is rather insensitive to our
poor knowledge of the source. This in turn allows us to establish in a source-independent way that some
absorption is occurring.
]. I
should stress the fact that the analysis of the combined X-ray/TeV-gamma-ray spectrum for the Markarian
421 blazar, as discussed in Ref. [333], provides rather compelling evidence. The X-ray part of the spectrum
allows one to predict the TeV-gamma-ray part of the spectrum in a way that is rather insensitive to our
poor knowledge of the source. This in turn allows us to establish in a source-independent way that some
absorption is occurring.
For the associated quantum-spacetime-phenomenology analysis, the fact that some absorption is
occurring does not allow us to infer much: the analysis will become more and more effective as
the quantitative characterization of the effectiveness of absorption becomes more and more
precise (as measured by the amount of deviation from the level of absorption expected within a
classical-spacetime analysis that would still be compatible with the observations). And we are
not yet ready to make any definite statement about this absorption levels. This is not only a
result of our rather poor knowledge of the IR diffuse extragalactic background, but it is also
due to the status of the observations, which still presents us with some apparent puzzles. For
example, it is not yet fully understood why, as observed by some [15, 355, 17, 536], there is a
difference between the absorption-induced cutoff energy found in data concerning Markarian 421,
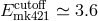 TeV, and the corresponding cutoff estimate obtained from Markarian-501 data,
TeV, and the corresponding cutoff estimate obtained from Markarian-501 data,
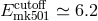 TeV. And the observation of TeV
TeV. And the observation of TeV  -rays emitted by the blazar H1426+428,
which is significantly more distant than Markarian 421 and Markarian 501, does show a level of
absorption that is higher than the ones inferred for Markarian 421 and Markarian 501, but (at least
assuming a certain description [16
-rays emitted by the blazar H1426+428,
which is significantly more distant than Markarian 421 and Markarian 501, does show a level of
absorption that is higher than the ones inferred for Markarian 421 and Markarian 501, but (at least
assuming a certain description [16 ] of the IR diffuse extragalactic background) the H1426+428 TeV
luminosity “seems to exceed the level anticipated from the current models of TeV blazars by
far” [16].
] of the IR diffuse extragalactic background) the H1426+428 TeV
luminosity “seems to exceed the level anticipated from the current models of TeV blazars by
far” [16].
Clearly, the situation requires further clarification, but it seems reasonable to expect that within a few years we
should fully establish facts such as “ -rays with energies up to 20 TeV are absorbed by the IR diffuse extragalactic
background”.18
This would imply that at least some photons with energy smaller than
-rays with energies up to 20 TeV are absorbed by the IR diffuse extragalactic
background”.18
This would imply that at least some photons with energy smaller than  200 meV can create an
electron-positron pair in collisions with a 20 TeV
200 meV can create an
electron-positron pair in collisions with a 20 TeV  -ray. In turn this would imply for the PKV0 test
theory, with
-ray. In turn this would imply for the PKV0 test
theory, with 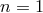 , that necessarily
, that necessarily  (i.e., either
(i.e., either  is positive or
is positive or 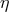 is negative with absolute
value smaller than 50). This means that this strategy of analysis will soon take us robustly to sensitivities
that are less than a factor of a 100 away from Planck-scale sensitivities, and it is natural to expect that
further refinements of these measurements will eventually take us to Planck-scale sensitivity and
beyond.
is negative with absolute
value smaller than 50). This means that this strategy of analysis will soon take us robustly to sensitivities
that are less than a factor of a 100 away from Planck-scale sensitivities, and it is natural to expect that
further refinements of these measurements will eventually take us to Planck-scale sensitivity and
beyond.
The line of reasoning needed to establish whether this Planck-scale sensitivity could apply to pure-kinematics frameworks is somewhat subtle. One could simplistically state that when we see a process that is forbidden by a certain set of laws of kinematics then those laws are falsified. However, in principle this statement is correct only when we have full knowledge of the process, including a full determination of the momenta of the incoming particles. In the case of the absorption of multi-TeV gamma rays from blazars it is natural to assume that this absorption be due to interactions with IR photons, but we are not in a position to exclude that the absorption be due to higher-energy background photons. Therefore, we should contemplate the possibility that the PKV0 kinematics be implemented within a framework in which the description of dynamics is such to introduce a large-enough modification of cross sections to allow absorption of multi-TeV blazar gamma rays by background photons of energy higher than 200 meV. As mentioned above repeatedly, I advocate a balanced perspective on these sorts of issues, which should not extend all the way to assuming wild conspiracies centered on very large changes in cross sections, even when testing a pure-kinematics framework. But, as long as a consensus on criteria for such a balanced approach is not established, it is difficult to attribute a quantitative confidence level to experimental bounds on a pure-kinematics framework through mere observation of some absorption of multi-TeV blazar gamma rays.
The concerns are not applicable to test theories that do provide a description of dynamics, such as the FTV0 test theory, with its effective-field-theory setup. However, for the FTV0 test theory one must take into account the fact that the modification of the dispersion relation carries the opposite sign to the two polarizations of the photon and might have an helicity dependence in the case of electrons and positrons. So, in the case of the FTV0 test theory, as long as observations only provide evidence of some absorption of TeV gamma rays (without much to say about the level of agreement with the amount of absorption expected in the classical-spacetime picture), and are, therefore, consistent with the hypothesis that only one of the polarizations of the photon is being absorbed, only rather weak limits can be established.
3.4.2 Threshold anomalies and modified energy-momentum conservation
For the derivation of threshold anomalies combining a modification of the law of energy-momentum
conservation with the modification of the dispersion relation can lead to results that are very different from
the case in which only the modifications of the dispersion relations are assumed. This is a feature already
stressed in the case of the analysis of photon stability. In order to establish it also for threshold anomalies
let me consider an example of the “DSR-inspired” modified law of energy-momentum conservation. I
assume that the modification of the law of energy-momentum conservation for the case of 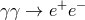 takes the form
takes the form
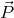 the momentum of the photon of energy
the momentum of the photon of energy 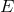 and I denote with
and I denote with 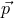 the momentum
of the photon of energy
the momentum
of the photon of energy  .
.
Using these (26 ), (27
), (27 ) and the “
) and the “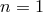 ” dispersion relation, one obtains (keeping only terms that are
meaningful for
” dispersion relation, one obtains (keeping only terms that are
meaningful for 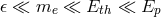 )
)
This shows very emphatically that modifications of the law of energy-momentum conservation can
compensate for the effects on threshold derivation produced by modified dispersion relations. The
cancellation should typically be only partial, but in cases in which the two modifications are “matched
exactly” there is no left-over effect. The fact that a DSR-inspired modification of the law of conservation of
energy-momentum produces this exact matching admits a tentative interpretation that the interested reader
can find in Refs. [58, 63 ].
].
3.5 Photopion production threshold anomalies and the cosmic-ray spectrum
In the preceding Section 3.4, I discussed the implications of possible Planck-scale effects for the process
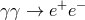 , but this is not the only process in which Planck-scale effects can be important. In particular,
there has been strong interest [327, 38
, but this is not the only process in which Planck-scale effects can be important. In particular,
there has been strong interest [327, 38 , 73
, 73 , 463
, 463 , 305, 59
, 305, 59 , 115
, 115 , 35, 431
, 35, 431 ] in the analysis of the “photopion
production” process,
] in the analysis of the “photopion
production” process, 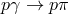 . As already stressed in Section 1.5, interest in the photopion-production
process originates from its role in our description of the high-energy portion of the cosmic-ray spectrum.
The “GZK cutoff” feature of that spectrum is linked directly to the value of the minimum (threshold)
energy required for cosmic-ray protons to produce pions in collisions with CMBR photons [267, 558] (see,
e.g., Refs. [240, 348]). The argument suggesting that Planck-scale modifications of the dispersion relation
may significantly affect the estimate of this threshold energy is completely analogous to that
discussed in preceding Section 3.4 for
. As already stressed in Section 1.5, interest in the photopion-production
process originates from its role in our description of the high-energy portion of the cosmic-ray spectrum.
The “GZK cutoff” feature of that spectrum is linked directly to the value of the minimum (threshold)
energy required for cosmic-ray protons to produce pions in collisions with CMBR photons [267, 558] (see,
e.g., Refs. [240, 348]). The argument suggesting that Planck-scale modifications of the dispersion relation
may significantly affect the estimate of this threshold energy is completely analogous to that
discussed in preceding Section 3.4 for 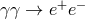 . However, the derivation is somewhat more
tedious: in the case of
. However, the derivation is somewhat more
tedious: in the case of 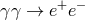 the calculations are simplified by the fact that both outgoing
particles have mass
the calculations are simplified by the fact that both outgoing
particles have mass 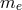 and both incoming particles are massless, whereas for the threshold
conditions for the photopion-production process one needs to handle the kinematics for a head-on
collision between a soft photon of energy
and both incoming particles are massless, whereas for the threshold
conditions for the photopion-production process one needs to handle the kinematics for a head-on
collision between a soft photon of energy  and a high-energy particle of mass
and a high-energy particle of mass 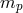 and
momentum
and
momentum 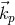 producing two (outgoing) particles with masses
producing two (outgoing) particles with masses 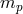 ,
,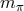 and momenta
and momenta
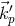 ,
,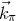 . The threshold can then be conveniently [73
. The threshold can then be conveniently [73 ] characterized as a relationship describing the
minimum value, denoted by
] characterized as a relationship describing the
minimum value, denoted by 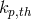 , that the spatial momentum of the incoming particle of mass
, that the spatial momentum of the incoming particle of mass
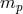 must have in order for the process to be allowed for given value
must have in order for the process to be allowed for given value  of the photon energy:
of the photon energy:
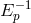 and/or the smallness of
and/or the smallness of  or
or
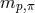 ).
).
Notice that whereas in discussing the pair-production threshold relevant for observations of TeV gamma
rays I had immediately specialized (13 ) to the case
) to the case  , here I am contemplating values of
, here I am contemplating values of 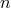 that are
even greater than 1. One could also admit
that are
even greater than 1. One could also admit 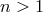 for the pair-production threshold analysis, but it would
be a mere academic exercise, since it is easy to verify that in that case Planck-scale sensitivity is within
reach only for
for the pair-production threshold analysis, but it would
be a mere academic exercise, since it is easy to verify that in that case Planck-scale sensitivity is within
reach only for  not significantly greater than 1. Instead (as I briefly stressed already in Section 1.5) the
role of the photopion-production threshold in cosmic-ray analysis is such that even for the case of
values of
not significantly greater than 1. Instead (as I briefly stressed already in Section 1.5) the
role of the photopion-production threshold in cosmic-ray analysis is such that even for the case of
values of 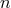 as high as 2 (i.e., even for the case of effects suppressed quadratically by the
Planck scale) Planck-scale sensitivity is not unrealistic. In fact, using for
as high as 2 (i.e., even for the case of effects suppressed quadratically by the
Planck scale) Planck-scale sensitivity is not unrealistic. In fact, using for 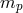 and
and  the
values of the masses of the proton and the pion and for
the
values of the masses of the proton and the pion and for  a typical CMBR-photon energy
one finds that for negative
a typical CMBR-photon energy
one finds that for negative 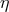 of order 1 (effects introduced at the Planck scale) the shift of
the threshold codified in (29
of order 1 (effects introduced at the Planck scale) the shift of
the threshold codified in (29 ) is gigantic for
) is gigantic for 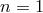 and still observably large [38
and still observably large [38 , 73
, 73 ] for
] for
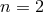 .
.
For negative 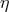 the Planck-scale correction shifts the photopion-production
threshold to higher values with respect to the standard classical-spacetime prediction,
which estimates the photopion-production threshold scale to be of about
the Planck-scale correction shifts the photopion-production
threshold to higher values with respect to the standard classical-spacetime prediction,
which estimates the photopion-production threshold scale to be of about  .
Assuming19
that the observed cosmic rays of highest energies are protons, when the spectrum reaches the
photopion-production threshold one should first encounter a pileup of cosmic rays with energies just in the
neighborhood of the threshold scale, and then above the threshold the spectrum should be severely
depleted. The pileup results from the fact that protons with above-threshold energy tend to lose energy
through photopion production and slow down until their energy is comparable to the threshold energy. The
depletion above the threshold is the counterpart of this pileup (protons emitted at the source with energy
above the threshold tend to reach us, if they come to us from far enough away, with energy comparable to
the threshold energy).
.
Assuming19
that the observed cosmic rays of highest energies are protons, when the spectrum reaches the
photopion-production threshold one should first encounter a pileup of cosmic rays with energies just in the
neighborhood of the threshold scale, and then above the threshold the spectrum should be severely
depleted. The pileup results from the fact that protons with above-threshold energy tend to lose energy
through photopion production and slow down until their energy is comparable to the threshold energy. The
depletion above the threshold is the counterpart of this pileup (protons emitted at the source with energy
above the threshold tend to reach us, if they come to us from far enough away, with energy comparable to
the threshold energy).
The availability in this cosmic-ray context of Planck-scale sensitivities for values of 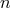 all the way up to
all the way up to
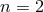 was fully established by the year 2000 [38, 73]. The debate then quickly focused on establishing
what exactly the observations were telling us about the photopion-production threshold. The fact that the
AGASA cosmic-ray observatory was reporting [519] evidence of a behavior of the spectrum that was of the
type expected in this Planck-scale picture generated a lot of interest. However, more recent cosmic-ray
observations, most notably the ones reported by the Pierre Auger observatory [448, 8], appear
to show no evidence of unexpected behavior. There is even some evidence [5
was fully established by the year 2000 [38, 73]. The debate then quickly focused on establishing
what exactly the observations were telling us about the photopion-production threshold. The fact that the
AGASA cosmic-ray observatory was reporting [519] evidence of a behavior of the spectrum that was of the
type expected in this Planck-scale picture generated a lot of interest. However, more recent cosmic-ray
observations, most notably the ones reported by the Pierre Auger observatory [448, 8], appear
to show no evidence of unexpected behavior. There is even some evidence [5 ] (see, however,
the updated Ref. [11
] (see, however,
the updated Ref. [11 ]) suggesting that to the highest-energy observed cosmic rays, one can
associate some relatively nearby sources, and that all this is occurring at scales that could
fit within the standard picture of the photopion-production threshold, without Planck scale
effects.
]) suggesting that to the highest-energy observed cosmic rays, one can
associate some relatively nearby sources, and that all this is occurring at scales that could
fit within the standard picture of the photopion-production threshold, without Planck scale
effects.
These results reported by the Pierre Auger Observatory are already somewhat beyond the “preliminary” status, and we should soon have at our disposal very robust cosmic-ray data, which should be easily converted into actual experimental bounds on the parameters of Planck-scale test theories.
Among the key ingredients that are still missing I should assign priority to the mentioned issue of
correlation of cosmic-ray observations with the large scale distribution of matter in the nearby
universe and the issue of the composition of cosmic rays (protons versus heavy nuclei). The
rapidly-evolving [5, 11] picture of correlations with matter in the nearby universe focuses on cosmic-ray
events with energy 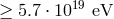 , while the growing evidence of a significant heavy-nuclei
component at high energies is limited so far at energies of
, while the growing evidence of a significant heavy-nuclei
component at high energies is limited so far at energies of 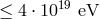 . And this state of
affairs, as notably stressed in Ref. [242], limits our insight on several issues relevant for the
understanding of the origin of cosmic rays and the related issues for tests of Lorentz symmetry,
since it leaves open several options for the nature and distance of the sources above and below
. And this state of
affairs, as notably stressed in Ref. [242], limits our insight on several issues relevant for the
understanding of the origin of cosmic rays and the related issues for tests of Lorentz symmetry,
since it leaves open several options for the nature and distance of the sources above and below
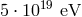 .
.
Postponing more definite claims on the situation on the experimental side, let me stress, however, that
there is indeed a lot at stake in these studies for the hypothesis of quantum-spacetime-induced Planck-scale
departures from Lorentz symmetry. Even for pure-kinematics test theories this type of data analysis is
rather strongly relevant. For example, the kinematics of the PKV0 test theory forbids (for negative 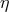 of
order 1 and
of
order 1 and 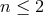 ) photopion production when the incoming proton energy is in the neighborhood of
) photopion production when the incoming proton energy is in the neighborhood of
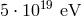 and the incoming photon has typical CMBR energies. For reasons already stressed (for other
contexts), in order to establish a robust experimental limit on pure-kinematics scenarios using the role of
the photopion-production threshold in the cosmic-ray spectrum, it would be necessary to also exclude that
other background photons (not necessarily CMBR photons) be responsible for the observed
cutoff.20
It appears likely that such a level of understanding of the cosmic-ray spectrum will be achieved in the
not-so-distant future.
and the incoming photon has typical CMBR energies. For reasons already stressed (for other
contexts), in order to establish a robust experimental limit on pure-kinematics scenarios using the role of
the photopion-production threshold in the cosmic-ray spectrum, it would be necessary to also exclude that
other background photons (not necessarily CMBR photons) be responsible for the observed
cutoff.20
It appears likely that such a level of understanding of the cosmic-ray spectrum will be achieved in the
not-so-distant future.
For the FTV0 test theory, since it goes beyond pure kinematics, one is not subject to similar concerns [381]. However, the fact that it admits the possibility of different effects for the two helicities of the incoming proton, complicates and renders less sharp this type of cosmic-ray analyses. It does lead to intriguing hypotheses: for example, exploiting the possibility of helicity dependence of the Planck scale effect for protons, one can rather naturally end up with a scenario that predicts a pileup/cutoff structure somewhat similar to the one of the standard classical-spacetime analysis, but softer, as a result of the fact that only roughly half of the protons would be allowed to lose energy by photopion production.
For the photopion-production threshold one finds exactly the same mechanism, which I discussed in
some detail for the pair-production threshold, of possible compensation between the effects produced by
modified dispersion relations and the effects produced by modified laws of energy-momentum conservation.
So, the analysis of frameworks where both the dispersion relation and the energy-momentum conservation
law are modified, as typical in DSR scenarios [63 ], should take into account that added element of
complexity.
], should take into account that added element of
complexity.
3.6 Pion non-decay threshold and cosmic-ray showers
Also relevant to the analysis of cosmic-ray observations is another aspect of the possible implications of
quantum-spacetime-motivated Planck-scale departures from Lorentz symmetry: the possibility of a
suppression of pion decay at ultrahigh energies. While in some cases departures from Lorentz symmetry
allow the decay of otherwise stable particles (as in the case of 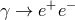 , discussed above, for appropriate
choice of values of parameters), it is indeed also possible for departures from Lorentz symmetry to
either introduce a threshold value of the energy of the particle, above which a certain decay
channel for that particle is totally forbidden [179
, discussed above, for appropriate
choice of values of parameters), it is indeed also possible for departures from Lorentz symmetry to
either introduce a threshold value of the energy of the particle, above which a certain decay
channel for that particle is totally forbidden [179 , 81
, 81 ], or introduce some sort of suppression
of the decay probability that increases with energy and becomes particularly effective above
a certain threshold value of the energy of the decaying particle [59
], or introduce some sort of suppression
of the decay probability that increases with energy and becomes particularly effective above
a certain threshold value of the energy of the decaying particle [59 , 115
, 115 , 244]. This may be
relevant [81
, 244]. This may be
relevant [81 , 59
, 59 ] for the description of the air showers produced by cosmic rays, whose structure
depends rather sensitively on certain decay probabilities, particularly the one for the decay
] for the description of the air showers produced by cosmic rays, whose structure
depends rather sensitively on certain decay probabilities, particularly the one for the decay
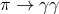 .
.
The possibility of suppression at ultrahigh energies of the decay 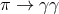 has been considered from the
quantum-gravity-phenomenology perspective primarily adopting PKV0-type frameworks [59
has been considered from the
quantum-gravity-phenomenology perspective primarily adopting PKV0-type frameworks [59 , 115]. Using
the kinematics of the PKV0 test theory one easily arrives [59
, 115]. Using
the kinematics of the PKV0 test theory one easily arrives [59 ] at the following relationship
between the opening angle
] at the following relationship
between the opening angle 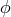 of the directions of the momenta of the outgoing photons, the
energy of the pion (
of the directions of the momenta of the outgoing photons, the
energy of the pion (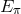 ) and the energies (
) and the energies (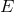 and
and 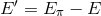 ) of the outgoing photons:
) of the outgoing photons:
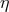 , at high energies the phase space available to the decay is
anomalously reduced: for a given value of
, at high energies the phase space available to the decay is
anomalously reduced: for a given value of 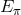 certain values of
certain values of 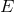 that would normally be accessible to
the decay are no longer accessible (they would require
that would normally be accessible to
the decay are no longer accessible (they would require 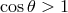 ). This anomaly starts to be noticeable at
pion energies of order
). This anomaly starts to be noticeable at
pion energies of order 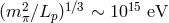 , but only very gradually (at first only a small portion of the
available phase space is excluded).
, but only very gradually (at first only a small portion of the
available phase space is excluded).
This is rather intriguing since there is a report [81 ] of experimental evidence of anomalies
for the structure of the air showers produced by cosmic rays, particularly their longitudinal
development. And it has been argued in Ref. [81] that these unexpected features of the longitudinal
development of air showers could be explained in terms of a severely reduced decay probability
for pions of energies of
] of experimental evidence of anomalies
for the structure of the air showers produced by cosmic rays, particularly their longitudinal
development. And it has been argued in Ref. [81] that these unexpected features of the longitudinal
development of air showers could be explained in terms of a severely reduced decay probability
for pions of energies of 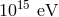 and higher. This is still to be considered a very preliminary
observation, not only because of the need to acquire data of better quality on the development of air
showers, but also because of the role [59] that our limited control of nonperturbative QCD
has in setting our expectations for what air-shower development should look like without new
physics.
and higher. This is still to be considered a very preliminary
observation, not only because of the need to acquire data of better quality on the development of air
showers, but also because of the role [59] that our limited control of nonperturbative QCD
has in setting our expectations for what air-shower development should look like without new
physics.
It is becoming rather “urgent” to reassess this issue in light of recent data on cosmic rays and cosmic-ray shower development. Such an exercise has not been made for a few years now, and for the mentioned Auger data, with the associated debate on the composition of cosmic rays, the analysis of shower development (and, therefore, of the hypothesis of some suppression of pion decay) is acquiring increasing significance [509, 6, 36, 549].
As for the other cases in which I discuss effects of modifications of the dispersion relation for kinematics of particle reactions, for this pion-decay argument scenarios hosting both a modified dispersion relation and modifications of the law of conservation of energy-momentum, as typical in DSR scenarios, can lead to [63] a compensation of the correction terms.
3.7 Vacuum Cerenkov and other anomalous processes
The quantum-spacetime-phenomenology analyses I have reviewed so far have played a particularly significant role in the rapid growth of the field of quantum-spacetime phenomenology over the last decade. This is particularly true for the analyses of the pair-production threshold for gamma rays and of the photopion-production threshold for cosmic rays, in which the data relevant for the Planck-scale effect under study can be perceived as providing some encouragement for new physics. One can legitimately argue [463, 302] that the observed level of absorption of TeV gamma rays is low enough to justify speculations about “new physics” (even though, as mentioned, there are “conventional-physics descriptions” of the relevant data). The opportunities for Planck scale physics to play a role in the neighborhood of the GZK scale of the cosmic-ray spectrum are becoming slimmer, as stressed in Section 3.5, but still it has been an important sign of maturity for quantum-spacetime phenomenology to play its part in the debate that for a while was generated by the preliminary and tentative indications of an anomaly around the “GZK cutoff”. It is interesting how the hypothesis of a pion-stability threshold, another Planck-scale-motivated hypothesis, also plays a role in the assessment of the present status of studies of ultra-high-energy cosmic rays.
I am giving disproportionate attention to the particle-interaction analyses described in Sections 3.4, 3.5, 3.6 because they are the most discussed and clearest evidence in support of the claim that quantum-spacetime Planck-scale phenomenology does have the ability to discover its target new physics, so much so that some (however tentative) “experimental puzzles” have been considered and are being considered from the quantum-spacetime perspective.
But it is of important to also consider the implications of quantum-spacetime-inspired Planck-scale
departures from Lorentz symmetry, and particularly Planck-scale modifications of the dispersion relation,
for all possible particle-physics processes. And a very valuable type of particle-physics processes
to be considered are the ones that are forbidden in a standard special-relativistic setup but
could be allowed in the presence of Planck-scale departures from Lorentz symmetry. These
processes could be called “anomalous processes”, and in the analysis of some of them one does find
opportunities for Planck-scale sensitivity, as already discussed for the case of the process  in
Section 3.3.
in
Section 3.3.
For a comprehensive list (and more detailed discussion) of other analyses of anomalous processes, which
are relevant for the whole subject of the study of possible departures from Lorentz symmetry
(within or without quantum spacetime), readers can rely on Refs. [395 , 308
, 308 ] and references
therein.
] and references
therein.
I will just briefly mention one more significant example of an anomalous process that is
relevant from a quantum-spacetime-phenomenology perspective: the “vacuum Cerenkov” process,
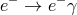 , which in certain scenarios [395
, which in certain scenarios [395 , 308
, 308 , 41] with broken Lorentz symmetry is allowed
above a threshold value of electron energy. This is analyzed in close analogy with the discussion
in Section 3.3 for the process
, 41] with broken Lorentz symmetry is allowed
above a threshold value of electron energy. This is analyzed in close analogy with the discussion
in Section 3.3 for the process 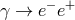 (which is another example of anomalous particle
interaction).
(which is another example of anomalous particle
interaction).
Since we have no evidence at present of vacuum-Cerenkov processes, the relevant analyses are of the type that sets limits on the parameters of some test theories. Clearly, this observational evidence against vacuum-Cerenkov processes is also relevant for pure-kinematics test theories, but in ways that it is difficult to quantify, because of the dependence on the strength of the interactions (an aspect of dynamics). So, here too, one should contemplate the implications of these findings from the perspective of the remarks offered in Section 3.3.1 concerning the plausibility (or lack thereof) of conspiracies between modifications of kinematics and modifications of the strengths of interaction.
Within the FTV0 test theory one can rigorously analyze the vacuum-Cerenkov process, and there
actually, if one arranges for opposite-sign dispersion-relation correction terms for the two helicities of the
electron, one can in principle have helicity-changing 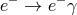 at any energy (no threshold), but
estimates performed [395
at any energy (no threshold), but
estimates performed [395 , 308
, 308 ] within the FTV0 test theory show that the rate is extremely small at low
energies.
] within the FTV0 test theory show that the rate is extremely small at low
energies.
Above the threshold for helicity-preserving 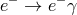 the FTV0 rates are substantial, and this in
particular would allow an analysis with Planck-scale sensitivity that relies on observations of 50-TeV
gamma rays from the Crab nebula. The argument is based on several assumptions (but all apparently
robust) and its effectiveness is somewhat limited by the combination of parameters allowed by FTV0 setup
and by the fact that for these 50-TeV gamma rays we observe from the Crab nebula we can only reasonably
guess a part of the properties of the emitting particles. According to the most commonly adopted model the
relevant gamma rays are emitted by the Crab nebula as a result of inverse Compton processes, and from
this one infers [395
the FTV0 rates are substantial, and this in
particular would allow an analysis with Planck-scale sensitivity that relies on observations of 50-TeV
gamma rays from the Crab nebula. The argument is based on several assumptions (but all apparently
robust) and its effectiveness is somewhat limited by the combination of parameters allowed by FTV0 setup
and by the fact that for these 50-TeV gamma rays we observe from the Crab nebula we can only reasonably
guess a part of the properties of the emitting particles. According to the most commonly adopted model the
relevant gamma rays are emitted by the Crab nebula as a result of inverse Compton processes, and from
this one infers [395 , 308
, 308 , 40] that for electrons of energies up to 50 TeV the vacuum Cerenkov process is
still ineffective, which in turn allows one to exclude certain corresponding regions of the FTV0 parameter
space.
, 40] that for electrons of energies up to 50 TeV the vacuum Cerenkov process is
still ineffective, which in turn allows one to exclude certain corresponding regions of the FTV0 parameter
space.
3.8 In-vacuo dispersion for photons
Analyses of thresholds for particle-physics processes, discussed in the previous Sections 3.4, 3.5, 3.6, and
3.7, played a particularly important role in the development of quantum-spacetime phenomenology over the
last decade, because the relevant studies were already at Planck-scale sensivity. In June 2008, with the
launch of the Fermi (/GLAST) space telescope [436, 201, 440, 3 , 4
, 4 , 413] we gained access to Planck-scale
effects also for in-vacuo dispersion as well. These studies deserve particular interest because they
have broad applicability to quantum-spacetime test theories of the fate of Lorentz/Poincaré
symmetry at the Planck scale. In the previous Sections 3.4, 3.5, 3.6, and 3.7, I stressed how the
analyses of thresholds for particle-physics processes provided information that is rather strongly
model dependent, and dependent on the specific choices of parameters within a given model.
The type of insight gained through in-vacuo-dispersion studies is instead significantly more
robust.
, 413] we gained access to Planck-scale
effects also for in-vacuo dispersion as well. These studies deserve particular interest because they
have broad applicability to quantum-spacetime test theories of the fate of Lorentz/Poincaré
symmetry at the Planck scale. In the previous Sections 3.4, 3.5, 3.6, and 3.7, I stressed how the
analyses of thresholds for particle-physics processes provided information that is rather strongly
model dependent, and dependent on the specific choices of parameters within a given model.
The type of insight gained through in-vacuo-dispersion studies is instead significantly more
robust.
A wavelength dependence of the speed of photons is obtained [66 , 497] from a modified dispersion
relation, if one assumes the velocity to still be described by
, 497] from a modified dispersion
relation, if one assumes the velocity to still be described by 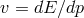 . In particular, from the dispersion
relation of the PKV0 test theory one obtains (at “intermediate energies”,
. In particular, from the dispersion
relation of the PKV0 test theory one obtains (at “intermediate energies”, 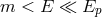 ) a velocity law of
the form
) a velocity law of
the form
 , 191]) and in the LQG literature
(see, e.g., Refs. [247, 33
, 191]) and in the LQG literature
(see, e.g., Refs. [247, 33 , 523]).
, 523]).
On the basis of the speed law (31 ) one would find that two simultaneously-emitted
photons should reach the detector at different times if they carry different energy. And this
time-of-arrival-difference effect can be significant [66
) one would find that two simultaneously-emitted
photons should reach the detector at different times if they carry different energy. And this
time-of-arrival-difference effect can be significant [66 , 491, 459
, 491, 459 , 539, 232] in the analysis of short-duration
gamma-ray bursts that reach us from cosmological distances. For a gamma-ray burst, it is not
uncommon22
that the time traveled before reaching our Earth detectors be of order
, 539, 232] in the analysis of short-duration
gamma-ray bursts that reach us from cosmological distances. For a gamma-ray burst, it is not
uncommon22
that the time traveled before reaching our Earth detectors be of order  . Microbursts within a
burst can have very short duration, as short as
. Microbursts within a
burst can have very short duration, as short as 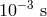 , and this should suggest that the photons that
compose such a microburst are all emitted at the same time, up to an uncertainty of
, and this should suggest that the photons that
compose such a microburst are all emitted at the same time, up to an uncertainty of 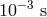 . Some of the
photons in these bursts have energies that extend even above [3
. Some of the
photons in these bursts have energies that extend even above [3 ] 10 GeV, and for two photons with energy
difference of order
] 10 GeV, and for two photons with energy
difference of order 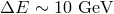 a
a 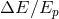 speed difference over a time of travel of
speed difference over a time of travel of 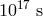 would lead [74
would lead [74 ] to a difference in times of arrival of order
] to a difference in times of arrival of order 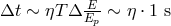 which is not
negligible23
with respect to the typical variability time scales one expects for the astrophysics of gamma-ray bursts.
Indeed, it is rather clear [74
which is not
negligible23
with respect to the typical variability time scales one expects for the astrophysics of gamma-ray bursts.
Indeed, it is rather clear [74 , 264] that the studies of gamma-ray bursts conducted by the Fermi
telescope provide us access to testing Planck-scale effects, in the linear-modification (“
, 264] that the studies of gamma-ray bursts conducted by the Fermi
telescope provide us access to testing Planck-scale effects, in the linear-modification (“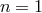 ”)
scenario.
”)
scenario.
These tests do not actually use Eq. (31 ) since for redshifts of 1 and higher, spacetime
curvature/expansion is a very tangible effect. And this introduces nonnegligible complications. Most results
in quantum-spacetime research hinting at modifications of the dispersion relation, and possible associated
energy/momentum dependence of the speed of massless particles, were derived working essentially in the
flat-spacetime/Minkowski limit: it is obvious that analogous effects would also be present when spacetime
expansion is switched on, but it is not obvious how formulas should be generalized to that case. In
particular, the formula (31
) since for redshifts of 1 and higher, spacetime
curvature/expansion is a very tangible effect. And this introduces nonnegligible complications. Most results
in quantum-spacetime research hinting at modifications of the dispersion relation, and possible associated
energy/momentum dependence of the speed of massless particles, were derived working essentially in the
flat-spacetime/Minkowski limit: it is obvious that analogous effects would also be present when spacetime
expansion is switched on, but it is not obvious how formulas should be generalized to that case. In
particular, the formula (31 ) is essentially unique for ultrarelativistic particles in the flat-spacetime limit:
we are only interested in leading-order formulas and the difference between
) is essentially unique for ultrarelativistic particles in the flat-spacetime limit:
we are only interested in leading-order formulas and the difference between 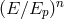 and
and
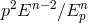 is negligible for ultrarelativistic particles (with
is negligible for ultrarelativistic particles (with 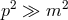 ). How spacetime expansion
renders these considerations more subtle is visible already in the case of de Sitter expansion.
Adopting conformal coordinates in de Sitter spacetime, with metric
). How spacetime expansion
renders these considerations more subtle is visible already in the case of de Sitter expansion.
Adopting conformal coordinates in de Sitter spacetime, with metric  (and
(and  ) we have for ultrarelativistic particles (with
) we have for ultrarelativistic particles (with 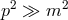 ) the velocity formula
) the velocity formula
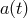 . It is not obvious how one should
describe leading-order Planck-scale corrections to this, going as some power of momentum. It is natural to
make the ansatz
with the integer
. It is not obvious how one should
describe leading-order Planck-scale corrections to this, going as some power of momentum. It is natural to
make the ansatz
with the integer 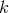 being at this point one more phenomenological parameter to be determined
experimentally. Arguments on value of the integer
being at this point one more phenomenological parameter to be determined
experimentally. Arguments on value of the integer 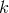 would be most “natural” were reported in
Refs. [228, 474, 303
would be most “natural” were reported in
Refs. [228, 474, 303 , 229
, 229 ], ultimately leading to a consensus [303, 229] converging on describing
], ultimately leading to a consensus [303, 229] converging on describing 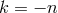 as the most natural choice. I shall not dwell much on this: let me just confirm that I would also give priority
to the case
as the most natural choice. I shall not dwell much on this: let me just confirm that I would also give priority
to the case 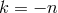 , but doing this in such a way as not to by-pass the obvious fact that the value of
, but doing this in such a way as not to by-pass the obvious fact that the value of  would have to be determined experimentally (and nature might well have chosen a value for
would have to be determined experimentally (and nature might well have chosen a value for 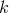 different
from
different
from 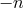 ).
).
Assuming that indeed 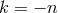 one would expect for simultaneously emitted massless particles in a
Universe parametrized by the cosmological parameters
one would expect for simultaneously emitted massless particles in a
Universe parametrized by the cosmological parameters 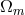 ,
,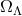 ,
, 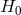 (evaluated today) a
momentum-dependent difference in times of arrival at a telescope given by
(evaluated today) a
momentum-dependent difference in times of arrival at a telescope given by
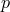 is the momentum of the particle when detected at the telescope.
is the momentum of the particle when detected at the telescope.
Actually, Planck-scale sensitivity to in-vacuo disperson can also be provided by observations of TeV
flares from certain active galactic nuclei, at redshifts much smaller than 1 (cases in which spacetime
expansion is not really tangible). In particular, studies of TeV flares from Mk 501 and PKS 2155–304
performed by the MAGIC [233] and HESS [285] observatories have established [218, 29, 226, 18, 10, 129]
bounds on the scale of dispersion, for the linear-effects (“ ”) scenario, at about
”) scenario, at about 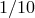 of the Planck
scale.
of the Planck
scale.
But the present best constraints on quantum-spacetime-induced in-vacuo dispersion are derived from
observations of gamma-ray bursts reported by the Fermi telescope. There are, so far, four Fermi-detected
gamma-ray bursts that are particularly significant for the hypothesis of in-vacuo dispersion:
GRB 090816C [3 ], GRB 090510 [4
], GRB 090510 [4 ], GRB 090902B [2
], GRB 090902B [2 ], GRB 090926A [482
], GRB 090926A [482 ]. The data for each one of
these bursts has the strength of constraining the scale of in-vacuo dispersion, for the linear-effects
(“
]. The data for each one of
these bursts has the strength of constraining the scale of in-vacuo dispersion, for the linear-effects
(“ ”) scenario, at better than
”) scenario, at better than  of the Planck scale. In particular, GRB 090510 was a truly
phenomenal short burst [4
of the Planck scale. In particular, GRB 090510 was a truly
phenomenal short burst [4 ] and the structure of its observation allows us to conservatively establish that
the scale of in-vacuo dispersion, for the linear-effects (“
] and the structure of its observation allows us to conservatively establish that
the scale of in-vacuo dispersion, for the linear-effects (“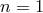 ”) scenario, is higher than 1.2 times the
Planck scale.
”) scenario, is higher than 1.2 times the
Planck scale.
The simplest way to do such analyses is to take one high-energy photon observed from the burst and
take as reference its delay  with respect to the burst trigger: if one could exclude conspiracies such that
the specific photon was emitted before the trigger (we cannot really exclude it, but we would
consider that as very unlikely, at least with present knowledge) evidently
with respect to the burst trigger: if one could exclude conspiracies such that
the specific photon was emitted before the trigger (we cannot really exclude it, but we would
consider that as very unlikely, at least with present knowledge) evidently  would have
to be bigger than any delay caused by the quantum-spacetime effects. This, in turn, allows
us, for the case of GRB 090510, to establish the limit at 1.2 times the Planck scale [4
would have
to be bigger than any delay caused by the quantum-spacetime effects. This, in turn, allows
us, for the case of GRB 090510, to establish the limit at 1.2 times the Planck scale [4 ]. And,
interestingly, even more sophisticated techniques of analysis, using not a single photon but the whole
structure of the high-energy observation of GRB 090510, also encourage the adoption of a limit at
1.2 times the Planck scale [4
]. And,
interestingly, even more sophisticated techniques of analysis, using not a single photon but the whole
structure of the high-energy observation of GRB 090510, also encourage the adoption of a limit at
1.2 times the Planck scale [4 ]. It has also been noticed [427
]. It has also been noticed [427 ] that if one takes at face value
the presence of high-energy photon bunches observed for GRB 090510, as evidence that these
photons were emitted nearly simultaneously at the source and they are being detected nearly
simultaneously, then the bound inferred could be even two orders of magnitude above the Planck
scale [427].
] that if one takes at face value
the presence of high-energy photon bunches observed for GRB 090510, as evidence that these
photons were emitted nearly simultaneously at the source and they are being detected nearly
simultaneously, then the bound inferred could be even two orders of magnitude above the Planck
scale [427].
I feel that at least the limit at 1.2 times the Planck scale is reasonably safe/conservative. But it is
obvious that here we would feel more comfortable with a wider collection of gamma-ray bursts usable for
our analyses. This would allow us to balance, using high statistics, the challenges for such studies of
in-vacuo dispersion that (as for other types of studies based on observations in astrophysics discussed
earlier) originate from the fact that we only have tentative models of the source of the signal. In particular,
the engine mechanisms causing the bursts of gamma rays also introduce correlations at the source
between the energy of the emitted photons and the time of their emission. This was in part
expected by some astrophysicists [459], and Fermi data allows one to infer it at levels even beyond
expectations [3 , 4
, 4 , 527, 376, 187, 256]. On a single observation of gamma-ray-burst events such
at-the-source correlations are, in principle, indistinguishable from the effect we expect from in-vacuo
dispersion, which indeed is a correlation between times of arrival and energies of the photons.
And another challenge I should mention originates from the necessity of understanding at least
partly the “precursors” of a gamma-ray burst, another feature that was already expected and to
some extent known [362], but recently came to be known as a more significant effect than
expected [4
, 527, 376, 187, 256]. On a single observation of gamma-ray-burst events such
at-the-source correlations are, in principle, indistinguishable from the effect we expect from in-vacuo
dispersion, which indeed is a correlation between times of arrival and energies of the photons.
And another challenge I should mention originates from the necessity of understanding at least
partly the “precursors” of a gamma-ray burst, another feature that was already expected and to
some extent known [362], but recently came to be known as a more significant effect than
expected [4 , 530].
, 530].
So, we will reach a satisfactory “comfort level” with our bounds on in-vacuo dispersion only with “high
statistics”, a relatively large collection [74 ] of gamma-ray bursts usable for our analyses. High statistics
always helps, but in this case it will also provide a qualitatively new handle for the data analysis: a
relatively large collection of high-energy gamma-ray bursts, inevitably distributed over different values
of redshift, would help our analyses also because comparison of bursts at different redshifts
can be exploited to achieve results that are essentially free from uncertainties originating from
our lack of knowledge of the sources. This is due to the fact that the structure of in-vacuo
dispersion is such that the effect should grow in predictable manner with redshift, whereas
we can exclude that the exact same dependence on redshift (if any) could characterize the
correlations at the source between the energy of the emitted photons and the time of their
emission.
] of gamma-ray bursts usable for our analyses. High statistics
always helps, but in this case it will also provide a qualitatively new handle for the data analysis: a
relatively large collection of high-energy gamma-ray bursts, inevitably distributed over different values
of redshift, would help our analyses also because comparison of bursts at different redshifts
can be exploited to achieve results that are essentially free from uncertainties originating from
our lack of knowledge of the sources. This is due to the fact that the structure of in-vacuo
dispersion is such that the effect should grow in predictable manner with redshift, whereas
we can exclude that the exact same dependence on redshift (if any) could characterize the
correlations at the source between the energy of the emitted photons and the time of their
emission.
In this respect we might be experiencing a case of tremendous bad luck: as mentioned we really still only
have four gamma-ray bursts to work with, GRB 090816C [3], GRB 090510 [4], GRB 090902B [2],
GRB 090926A [482], but on the basis of how Fermi observations had been going for the first 13 months of
operation we were led to hope that by this time (end of 2012), after 50 months of operation of
Fermi, we might have had as many as 15 such bursts and perhaps 4 or 5 bursts of outstanding
interest for in-vacuo dispersion, comparable to GRB 090510. These four bursts we keep using
from the Fermi data set were observed during the first 13 months of operation (in particular
GRB 090510 was observed during the 10th month of operation) and we got from Fermi nothing else
of any use over the last 37 months. If our luck turns around we should be able to claim for
quantum-spacetime phenomenology a first small but tangible success: ruling out at least the specific
hypothesis of Planck-scale in-vacuo dispersion, at least specifically for the case of linear-effects
(“ ”).
”).
This being said about the opportunities and challenges facing the phenomenology of in-vacuo dispersion,
let me, in closing this section, offer a few additional remarks on the broader picture. From a
quantum-spacetime-phenomenology perspective it is noteworthy that, while in the analyses discussed in the
previous Sections 3.4, 3.5, 3.6, and 3.7, the amplifier of the Planck-scale effect was provided by a large
boost, in this in-vacuo-dispersion case the amplification is due primarily to the long propagation times,
which essentially render the analysis sensitive to the accumulation [52 ] of very many minute Planck-scale
effects. For propagation times that are realistic in controlled Earth experiments, in which one
perhaps could manage to study the propagation of photons of TeV energies, over distances of
] of very many minute Planck-scale
effects. For propagation times that are realistic in controlled Earth experiments, in which one
perhaps could manage to study the propagation of photons of TeV energies, over distances of
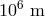 , the in-vacuo dispersion would still induce, even for
, the in-vacuo dispersion would still induce, even for 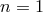 , only time delays of order
, only time delays of order
 .
.
In-vacuo-dispersion analyses of gamma-ray bursts are also extremely popular within the
quantum-spacetime-phenomenology community because of the very limited number of assumptions on
which they rely. One comes very close to having a direct test of a Planck-scale modification of the dispersion
relation. In comparing the PKV0 and the FTV0 test theories, one could exploit the fact that whereas
for the PKV0 test theory the Planck-scale-induced time-of-arrival difference would affect a
multi-photon microburst by producing a difference in the “average arrival time” of the signal in
different energy channels, within the FTV0 test theory, for an ideally unpolarized signal, one
would expect a dependence of the time-spread of a microburst that grows with energy, but
no effect for the average arrival time in different energy channels. This originates from the
polarization dependence imposed by the structure of the FTV0 test theory: for low-energy
channels the whole effect will be small, but in the highest-energy channels, the fact that the two
polarizations travel at different speed will manifest itself as spreading in time of the signal,
without any net average-time-of-arrival effect for an ideally unpolarized signal. Since there is
evidence that at least some gamma-ray bursts are somewhat far from being ideally unpolarized
(see evidence of polarization reported, e.g., in Refs. [359 , 556
, 556 , 528
, 528 ]), one could also exploit a
powerful correlation: within the FTV0 test theory one expects to find some bursts with sizeable
energy-dependent average-time-of-arrival differences between energy channels (for bursts with some
predominant polarization), and some bursts (the ones with no net polarization) with much less
average-time-of-arrival differences between energy channels but a sizeable difference in time
spreading in the different channels. Polarization-sensitive observations of gamma-ray bursts
would allow one to look directly for the polarization dependence predicted by the FTV0 test
theory.
]), one could also exploit a
powerful correlation: within the FTV0 test theory one expects to find some bursts with sizeable
energy-dependent average-time-of-arrival differences between energy channels (for bursts with some
predominant polarization), and some bursts (the ones with no net polarization) with much less
average-time-of-arrival differences between energy channels but a sizeable difference in time
spreading in the different channels. Polarization-sensitive observations of gamma-ray bursts
would allow one to look directly for the polarization dependence predicted by the FTV0 test
theory.
Clearly, these in-vacuo dispersion studies using gamma rays in the GeV–TeV range provide us at present
with the cleanest opportunity to look for Planck-scale modifications of the dispersion relation.
Unfortunately, while they do provide us comfortably with Planck-scale sensitivity to linear ( )
modifications of the dispersion relation, they are unable to probe significantly the case of quadratic
(
)
modifications of the dispersion relation, they are unable to probe significantly the case of quadratic
(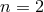 ) modifications.
) modifications.
And, while, as stressed, these studies apply to a wide range of quantum-spacetime scenarios with
modified dispersion relations, mostly as a result of their insensitivity to the whole issue of description of
dynamical aspects of a quantum-spacetime theory, one should be aware of the fact that it might be
inappropriate to characterize these studies as tests that must necessarily apply to all quantum-spacetime
pictures with modified dispersion relations. Most notably, the assumption of obtaining the velocity law from
the dispersion relation through the formula 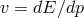 may or may not be valid in a given
quantum-spacetime picture. Validity of the formula
may or may not be valid in a given
quantum-spacetime picture. Validity of the formula  essentially requires that the theory is still
“Hamiltonian”, at least in the sense that the velocity along the
essentially requires that the theory is still
“Hamiltonian”, at least in the sense that the velocity along the 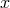 axis is obtained from the
commutator with a Hamiltonian (
axis is obtained from the
commutator with a Hamiltonian (![vx ∼ [x, H ]](article400x.gif) ), and that the Heisenberg commutator preserves
its standard form (
), and that the Heisenberg commutator preserves
its standard form (![[x,px] ∼ ¯h](article401x.gif) so that
so that 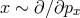 ). Especially this second point is rather
significant since heuristic arguments of the type also used to motivate modified dispersion relations
suggest [22, 122, 323
). Especially this second point is rather
significant since heuristic arguments of the type also used to motivate modified dispersion relations
suggest [22, 122, 323 , 415, 243, 408] that the Heisenberg commutator might have to be modified in the
quantum-spacetime realm.
, 415, 243, 408] that the Heisenberg commutator might have to be modified in the
quantum-spacetime realm.
3.9 Quadratic anomalous in-vacuo dispersion for neutrinos
Observations of gamma rays in the GeV–TeV range could provide us with a very sharp picture of
Planck-scale-induced dispersion, if it happens to be a linear (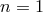 ) effect, but, as stressed above, one
would need observations of similar quality for photons of significantly higher energies in order to gain access
to scenarios with quadratic (
) effect, but, as stressed above, one
would need observations of similar quality for photons of significantly higher energies in order to gain access
to scenarios with quadratic ( ) effects of Planck-scale-induced dispersion. The prospect of observing
photons with energies up to
) effects of Planck-scale-induced dispersion. The prospect of observing
photons with energies up to 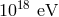 at ground observatories [471, 74
at ground observatories [471, 74 ] is very exciting, and should be
pursued very forcefully [74
] is very exciting, and should be
pursued very forcefully [74 ], but it represents an opportunity whose viability still remains to be fully
established. And in any case we expect photons of such high energies to be absorbed rather efficiently by
background soft photons (e.g., CMBR photons) so that we could not observe them from very distant
sources.
], but it represents an opportunity whose viability still remains to be fully
established. And in any case we expect photons of such high energies to be absorbed rather efficiently by
background soft photons (e.g., CMBR photons) so that we could not observe them from very distant
sources.
One possibility that could be considered [65 ] is the one of 1987a-type supernovae; however such
supernovae are typically seen at distances not greater than some
] is the one of 1987a-type supernovae; however such
supernovae are typically seen at distances not greater than some  light years. And the fact that
neutrinos from 1987a-type supernovae can be definitely observed up to energies of at least tens of TeV’s is
not enough to compensate for the smallness of the distances (as compared to typical gamma-ray-burst
distances). As a result, using 1987a-type supernovae one might have serious difficulties [65] even to achieve
Planck-scale sensitivity for linear (
light years. And the fact that
neutrinos from 1987a-type supernovae can be definitely observed up to energies of at least tens of TeV’s is
not enough to compensate for the smallness of the distances (as compared to typical gamma-ray-burst
distances). As a result, using 1987a-type supernovae one might have serious difficulties [65] even to achieve
Planck-scale sensitivity for linear (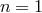 ) modifications of the dispersion relation, and going beyond linear
order clearly is not possible.
) modifications of the dispersion relation, and going beyond linear
order clearly is not possible.
The most advanced plans for in-vacuo-dispersion studies with sensitivity up to quadratic ( )
Planck-scale modifications of the dispersion relation actually exploit [230, 168, 61, 301
)
Planck-scale modifications of the dispersion relation actually exploit [230, 168, 61, 301 ] (also see, for a
similar argument within a somewhat different framework, Ref. [116]) once again the extraordinary
properties of gamma-ray bursters, but their neutrino emissions rather than their production of photons.
Indeed, according to current models [411, 543], gamma-ray bursters should also emit a substantial
amount of high-energy neutrinos. Some neutrino observatories should soon observe neutrinos
with energies between
] (also see, for a
similar argument within a somewhat different framework, Ref. [116]) once again the extraordinary
properties of gamma-ray bursters, but their neutrino emissions rather than their production of photons.
Indeed, according to current models [411, 543], gamma-ray bursters should also emit a substantial
amount of high-energy neutrinos. Some neutrino observatories should soon observe neutrinos
with energies between 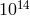 and
and 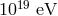 , and one could either (as it appears to be more
feasible [301]) compare the times of arrival of these neutrinos emitted by gamma-ray bursters to
the corresponding times of arrival of low-energy photons or compare the times of arrivals of
different-energy neutrinos (which, however, might require larger statistics than it seems natural to
expect).
, and one could either (as it appears to be more
feasible [301]) compare the times of arrival of these neutrinos emitted by gamma-ray bursters to
the corresponding times of arrival of low-energy photons or compare the times of arrivals of
different-energy neutrinos (which, however, might require larger statistics than it seems natural to
expect).
In assessing the significance of these foreseeable studies of neutrino propagation within different test
theories, one should again take into account issues revolving around the possibility of anomalous
reactions. In particular, in spite of the weakness of their interactions with other particles, within an
effective-field-theory setup neutrinos can be affected by Cherenkov-like processes at levels that are
experimentally significant [175], though not if the scale of modification of the dispersion relation is as high
as the Planck scale. The recent overall analysis of modified dispersion for neutrinos in quantum field theory
given in Ref. [379] shows that for the linear (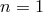 ) case we are presently able to establish constraints at
levels of about
) case we are presently able to establish constraints at
levels of about  times the Planck scale (and even further from the Planck scale for the quadratic case,
times the Planck scale (and even further from the Planck scale for the quadratic case,
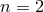 ).
).
3.10 Implications for neutrino oscillations
It is well established [179 , 141
, 141 , 225
, 225 , 83, 421
, 83, 421 , 169] that flavor-dependent modifications to the
energy-momentum dispersion relations for neutrinos may lead to neutrino oscillations even if neutrinos are
massless. This point is not directly relevant for the three test theories I have chosen to use as frameworks of
reference for this review. The PKV0 test theory adopts universality of the modification of the dispersion
relation, and also the FTV0 test theory describes flavor-independent effects (its effects are
“nonuniversal” only in relation to polarization/helicity). Still, I should mention this possibility
both because clearly flavor-dependent effects may well attract gradually more interest from
quantum-spacetime phenomenologists (some valuable analyses have already been produced; see, e.g.,
Refs. [395
, 169] that flavor-dependent modifications to the
energy-momentum dispersion relations for neutrinos may lead to neutrino oscillations even if neutrinos are
massless. This point is not directly relevant for the three test theories I have chosen to use as frameworks of
reference for this review. The PKV0 test theory adopts universality of the modification of the dispersion
relation, and also the FTV0 test theory describes flavor-independent effects (its effects are
“nonuniversal” only in relation to polarization/helicity). Still, I should mention this possibility
both because clearly flavor-dependent effects may well attract gradually more interest from
quantum-spacetime phenomenologists (some valuable analyses have already been produced; see, e.g.,
Refs. [395 , 308
, 308 ] and references therein), and because even for researchers focusing on flavor-independent
effects, it is important to be familiar with constraints that may be set on flavor-dependent
scenarios (those constraints, in a certain sense, provide motivation for the adoption of flavor
independence).
] and references therein), and because even for researchers focusing on flavor-independent
effects, it is important to be familiar with constraints that may be set on flavor-dependent
scenarios (those constraints, in a certain sense, provide motivation for the adoption of flavor
independence).
Most studies of neutrino oscillations induced by violations of Lorentz symmetry were actually not motivated
by quantum-gravity/quantum-spacetime research (they were part of the general Lorentz-symmetry-test
research area) and assumed that the flavor-dependent violations would take the form of a flavor-dependent
speed-of-light scale [179 ], which essentially corresponds to the adoption of a dispersion relation of the
type (13
], which essentially corresponds to the adoption of a dispersion relation of the
type (13 ), but with
), but with 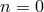 , and flavor-dependent values of
, and flavor-dependent values of  . A few studies have considered the
case24
. A few studies have considered the
case24
 with flavor-dependent
with flavor-dependent  , which is instead mainly of interest from a quantum-spacetime
perspective,25
and found [141
, which is instead mainly of interest from a quantum-spacetime
perspective,25
and found [141 , 225, 421
, 225, 421 ] that for
] that for 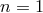 from Eq. (13
from Eq. (13 ) one naturally ends up with oscillations lengths
that depend quadratically on the inverse of the energies of the particles (
) one naturally ends up with oscillations lengths
that depend quadratically on the inverse of the energies of the particles ( ), whereas in the case
), whereas in the case
 (flavor-dependent speed-of-light scale) such a strong dependence on the inverse of the energies is
not possible [141
(flavor-dependent speed-of-light scale) such a strong dependence on the inverse of the energies is
not possible [141 ]. In principle, this opens an opportunity for the discovery of manifestations of the
flavor-dependent
]. In principle, this opens an opportunity for the discovery of manifestations of the
flavor-dependent 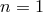 case through studies of neutrino oscillations [141
case through studies of neutrino oscillations [141 , 421
, 421 ]; however, at
present there is no evidence of a role for these effects in neutrino oscillations and, therefore,
the relevant data analyses produce bounds [141, 421] on flavor dependence of the dispersion
relation.
]; however, at
present there is no evidence of a role for these effects in neutrino oscillations and, therefore,
the relevant data analyses produce bounds [141, 421] on flavor dependence of the dispersion
relation.
In a part of the next section (4.6), I shall comment again on neutrino oscillations, but in relation to the possible role of quantum-spacetime-induced decoherence (rather than Lorentz-symmetry violations).
3.11 Synchrotron radiation and the Crab Nebula
Another opportunity to set limits on test theories with Planck-scale modified dispersion relations
is provided by the study of the implications of modified dispersion relations for synchrotron
radiation [306 , 62
, 62 , 309
, 309 , 378
, 378 , 231, 420, 39]. An important point for these analyses [306
, 231, 420, 39]. An important point for these analyses [306 , 309, 378
, 309, 378 ] is the
observation that in the conventional (Lorentz-invariant) description of synchrotron radiation one can
estimate the characteristic energy
] is the
observation that in the conventional (Lorentz-invariant) description of synchrotron radiation one can
estimate the characteristic energy 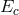 of the radiation through a semi-heuristic derivation [300] leading to
the formula
of the radiation through a semi-heuristic derivation [300] leading to
the formula
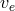 is the speed of the electron,
is the speed of the electron, 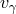 is the speed of the photon,
is the speed of the photon,  is the angle of outgoing
radiation, and
is the angle of outgoing
radiation, and 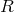 is the radius of curvature of the trajectory of the electron.
is the radius of curvature of the trajectory of the electron.
Assuming that the only Planck-scale modification in this formula should come from the velocity law
(described using 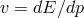 in terms of the modified dispersion relation), one finds that in some instances
the characteristic energy of synchrotron radiation may be significantly modified by the presence of
Planck-scale modifications of the dispersion relation. This originates from the fact that, for example,
according to (31
in terms of the modified dispersion relation), one finds that in some instances
the characteristic energy of synchrotron radiation may be significantly modified by the presence of
Planck-scale modifications of the dispersion relation. This originates from the fact that, for example,
according to (31 ), for
), for  and
and 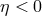 , an electron cannot have a speed that exceeds the
value
, an electron cannot have a speed that exceeds the
value 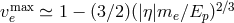 , whereas in SR
, whereas in SR  can take values arbitrarily close to
1.
can take values arbitrarily close to
1.
As an opportunity to test such a modification of the value of the synchrotron-radiation characteristic
energy one can attempt to use data [306 ] on photons emitted by the Crab nebula. This must be
done with caution since the observational information on synchrotron radiation being emitted
by the Crab nebula is rather indirect: some of the photons we observe from the Crab nebula
are attributed to sychrotron processes, but only on the basis of a (rather successful) model,
and the value of the relevant magnetic fields is also not directly measured. But the level of
Planck-scale sensitivity that could be within the reach of this type of analysis is truly impressive:
assuming that indeed the observational situation has been properly interpreted, and relying on the
mentioned assumption that the only modification to be taken into account is the one of the
velocity law, one could [306, 378
] on photons emitted by the Crab nebula. This must be
done with caution since the observational information on synchrotron radiation being emitted
by the Crab nebula is rather indirect: some of the photons we observe from the Crab nebula
are attributed to sychrotron processes, but only on the basis of a (rather successful) model,
and the value of the relevant magnetic fields is also not directly measured. But the level of
Planck-scale sensitivity that could be within the reach of this type of analysis is truly impressive:
assuming that indeed the observational situation has been properly interpreted, and relying on the
mentioned assumption that the only modification to be taken into account is the one of the
velocity law, one could [306, 378 ] set limits on the parameter
] set limits on the parameter 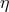 of the PKV0 test theory that
go several orders of magnitude beyond
of the PKV0 test theory that
go several orders of magnitude beyond 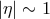 , for negative
, for negative  and
and  , and even for
quadratic (
, and even for
quadratic (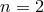 ) Planck-scale modifications the analysis would fall “just short” of reaching
Planck-scale sensitivity (“only” a few orders of magnitude away from
) Planck-scale modifications the analysis would fall “just short” of reaching
Planck-scale sensitivity (“only” a few orders of magnitude away from 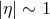 sensitivity for
sensitivity for
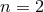 ).
).
However, the assumptions of this type of analysis, particularly the assumption that nothing changes but
the velocity law, cannot even be investigated within pure-kinematics test theories, such as the PKV0 test
theory. Synchrotron radiation is due to the acceleration of the relevant charged particles and,
therefore, implicit in the derivation of the formula (35 ) is a subtle role for dynamics [62]. From a
quantum-field-theory perspective, the process of synchrotron-radiation emission can be described in terms of
Compton scattering of the electrons with the virtual photons of the magnetic field, and its analysis
is, therefore, rather sensitive even to details of the description of dynamics in a given theory.
Indeed, essentially this synchrotron-radiation phenomenology has focused on the FTV0 test
theory and its generalizations, so that one can rely on the familiar formalism of quantum field
theory. Making reasonably prudent assumptions on the correct model of the source one can
establish [378] valuable (sub-Planckian!) experimental bounds on the parameters of the FTV0 test
theory.
) is a subtle role for dynamics [62]. From a
quantum-field-theory perspective, the process of synchrotron-radiation emission can be described in terms of
Compton scattering of the electrons with the virtual photons of the magnetic field, and its analysis
is, therefore, rather sensitive even to details of the description of dynamics in a given theory.
Indeed, essentially this synchrotron-radiation phenomenology has focused on the FTV0 test
theory and its generalizations, so that one can rely on the familiar formalism of quantum field
theory. Making reasonably prudent assumptions on the correct model of the source one can
establish [378] valuable (sub-Planckian!) experimental bounds on the parameters of the FTV0 test
theory.
3.12 Birefringence and observations of polarized radio galaxies
As I stressed already a few times earlier in this review, the FTV0 test theory, as a result of a rigidity of the
adopted effective-field-theory framework, necessarily predicts birefringence, by assigning different speeds to
different photon polarizations. Birefringence is a pure-kinematics effect, so it can also be included in
straightforward generalizations of the PKV0 test theory, if one assigns a different dispersion relation to
different photon polarizations and then assumes that the speed is obtained from the dispersion relation via
the standard  relation.
relation.
I have already discussed some ways in which birefringence may affect other tests of dispersion-inducing (energy-dependent) modifications of the dispersion relation, as in the example of searches of time-of-arrival/energy correlations for observations of gamma-ray bursts. The applications I already discussed use the fact that for large enough travel times birefringence essentially splits a group of simultaneously-emitted photons with roughly the same energy and without characteristic polarization into two temporally and spatially separated groups of photons, with different circular polarization (one group being delayed with respect to the other as a result of the polarization-dependent speed of propagation).
Another feature that can be exploited is the fact that even for travel times that are somewhat shorter
than the ones achieving a separation into two groups of photons, the same type of birefringence can already
effectively erase [261 , 262
, 262 ] any linear polarization that might have been there to begin with, when the
signal was emitted. This observation can be used in turn to argue that for given magnitude of the
birefringence effects and given values of the distance from the source it should be impossible
to observe linearly polarized light, since the polarization should have been erased along the
way.
] any linear polarization that might have been there to begin with, when the
signal was emitted. This observation can be used in turn to argue that for given magnitude of the
birefringence effects and given values of the distance from the source it should be impossible
to observe linearly polarized light, since the polarization should have been erased along the
way.
Using observations of polarized light from distant radio galaxies [395 , 261
, 261 , 262
, 262 , 158, 342, 495] one can
comfortably achieve Planck-scale sensitivity (for “
, 158, 342, 495] one can
comfortably achieve Planck-scale sensitivity (for “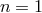 ” linear modifications of the dispersion relation)
to birefringence effects following this strategy. In particular, the analysis reported in Ref. [261, 262] leads
to a limit of
” linear modifications of the dispersion relation)
to birefringence effects following this strategy. In particular, the analysis reported in Ref. [261, 262] leads
to a limit of 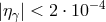 on the parameter
on the parameter 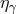 of the FTV0 test theory. And more recent studies of
this type allowed even more stringent bounds to be established(see Refs. [395
of the FTV0 test theory. And more recent studies of
this type allowed even more stringent bounds to be established(see Refs. [395 , 365] and references
therein).
, 365] and references
therein).
Interestingly, even for this strategy based on the effect of removal of linear polarization, gamma-ray
bursts could in principle provide formidable opportunities. And there was a report [173 ] of observation of
polarized MeV gamma rays in the prompt emission of the gamma-ray burst GRB 021206, which would
have allowed very powerful bounds on energy-dependent birefringence to be established. However, Ref. [173]
has been challenged (see, e.g., Ref. [481, 124]). Still, experimental studies of polarization for gamma-ray
bursts continue to be a very active area of research (see, e.g., Refs. [359, 556, 528]), and it is likely
that this will gradually become the main avenue for constraining quantum-spacetime-induced
birefringence.
] of observation of
polarized MeV gamma rays in the prompt emission of the gamma-ray burst GRB 021206, which would
have allowed very powerful bounds on energy-dependent birefringence to be established. However, Ref. [173]
has been challenged (see, e.g., Ref. [481, 124]). Still, experimental studies of polarization for gamma-ray
bursts continue to be a very active area of research (see, e.g., Refs. [359, 556, 528]), and it is likely
that this will gradually become the main avenue for constraining quantum-spacetime-induced
birefringence.
3.13 Testing modified dispersion relations in the lab
Over this past decade there has been growing awareness of the fact that data analyses with good sensitivity to effects introduced genuinely at the Planck scale are not impossible, as once thought. It is at this point well known, even outside the quantum-gravity/quantum-spacetime community, that Planck-scale sensitivity is achieved in certain (however rare) astrophysics studies. It would be very very valuable if we could establish the availability of analogous tests in controlled laboratory setups, but this is evidently more difficult, and opportunities are rare and of limited reach. Still, I feel it is important to keep this goal as a top priority, so in this Section I mention a couple of illustrative examples, which can at least show that laboratory tests are possible. Considering these objectives it makes sense to focus again on quantum-spacetime-motivated Planck-scale modifications of the dispersion relation, so that the estimates of sensitivity levels achievable in a controlled laboratory setup can be compared to the corresponding studies in astrophysics.
One possibility is to use laser-light interferometry to look for in-vacuo-dispersion effects. In Ref. [68 ] two
examples of interferometric setups were discussed in some detail, with the common feature of making use of
a frequency doubler, so that part of the beam would be for a portion of its journey through the
interferometer at double the reference frequency of the laser beam feeding the interferometer. The setups
must be such that the interference pattern is sensitive to the fact that, as a result of in-vacuo
dispersion, there is a nonlinear relation between the phase advancement of a beam at frequency
] two
examples of interferometric setups were discussed in some detail, with the common feature of making use of
a frequency doubler, so that part of the beam would be for a portion of its journey through the
interferometer at double the reference frequency of the laser beam feeding the interferometer. The setups
must be such that the interference pattern is sensitive to the fact that, as a result of in-vacuo
dispersion, there is a nonlinear relation between the phase advancement of a beam at frequency 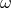 and a beam at frequency
and a beam at frequency 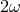 . For my purposes here it suffices to discuss briefly one such
interferometric setup. Specifically, let me give a brief description of a setup in which the frequency (or
energy) is the parameter characterizing the splitting of the photon state, so the splitting is in
energy space (rather than the more familiar splitting in configuration space, in which two parts
of the beam actually follow geometrically different paths). The frequency doubling could be
accomplished using a “second harmonic generator” [487] so that if a wave reaches the frequency
doubler with frequency
. For my purposes here it suffices to discuss briefly one such
interferometric setup. Specifically, let me give a brief description of a setup in which the frequency (or
energy) is the parameter characterizing the splitting of the photon state, so the splitting is in
energy space (rather than the more familiar splitting in configuration space, in which two parts
of the beam actually follow geometrically different paths). The frequency doubling could be
accomplished using a “second harmonic generator” [487] so that if a wave reaches the frequency
doubler with frequency 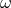 then, after passing through the frequency doubler, the outgoing
wave in general consists of two components, one at frequency
then, after passing through the frequency doubler, the outgoing
wave in general consists of two components, one at frequency 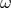 and the other at frequency
and the other at frequency
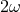 .
.
If two such frequency doublers are placed along the path of the beam at the end, one has a beam with
several components, two of which have frequency  : the transmission of the component that
left the first frequency doubler as a
: the transmission of the component that
left the first frequency doubler as a 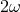 wave, and another component that is the result of
frequency doubling of that part of the beam that went through the first frequency doubler without
change in the frequency. Therefore, the final
wave, and another component that is the result of
frequency doubling of that part of the beam that went through the first frequency doubler without
change in the frequency. Therefore, the final 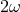 beam represents an interferometer in energy
space.
beam represents an interferometer in energy
space.
As shown in detail in Ref. [68 ] the intensity of this
] the intensity of this 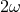 beam takes a form of type
beam takes a form of type
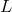 is the distance between the two frequency doublers,
is the distance between the two frequency doublers, 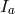 and
and 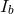 are
are 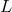 -independent (they
depend on the amplitude of the original wave and the effectiveness of the frequency doublers [68
-independent (they
depend on the amplitude of the original wave and the effectiveness of the frequency doublers [68 ]), the
phase
]), the
phase 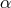 is also
is also 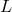 -independent and is obtained combining several contributions to the phase (both a
contribution from the propagation of the wave and a contribution introduced by the frequency
doublers [68
-independent and is obtained combining several contributions to the phase (both a
contribution from the propagation of the wave and a contribution introduced by the frequency
doublers [68 ]),
]), 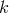 is the wave number corresponding to the frequency
is the wave number corresponding to the frequency 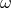 through the dispersion relation,
and
through the dispersion relation,
and 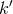 is the wave number corresponding to the frequency
is the wave number corresponding to the frequency 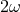 through the dispersion relation (since the
dispersion relation is Planck-scale modified one expects departures from the special-relativistic result
through the dispersion relation (since the
dispersion relation is Planck-scale modified one expects departures from the special-relativistic result
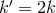 ).
).
Since the intensity only depends on the distance  between the frequency doublers through
the Planck-scale correction to the phase,
between the frequency doublers through
the Planck-scale correction to the phase, 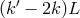 , by exploiting a setup that allows one
to vary
, by exploiting a setup that allows one
to vary 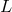 , one should rather easily disentangle the Planck-scale effect. And one finds [68]
that the accuracy achievable with modern interferometers is sufficient to achieve Planck-scale
sensitivity (e.g., sensitivity to
, one should rather easily disentangle the Planck-scale effect. And one finds [68]
that the accuracy achievable with modern interferometers is sufficient to achieve Planck-scale
sensitivity (e.g., sensitivity to 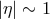 in the PKV0 test theory with
in the PKV0 test theory with  ). It is rather
optimistic to assume that the accuracy achieved in standard interferometers would also be
achievable with this peculiar setup, particularly since it would require the optics aspects of
the setup (such as lenses) to work with that high accuracy simultaneously with two beams of
different wavelength. Moreover, it would require some very smart techniques to vary the distance
between the frequency doublers without interfering with the effectiveness of the optics aspects
of the setup. So, in practice we would not presently be capable of using such setups to set
Planck-scale-sensitive limits on in-vacuo dispersion, but the fact that the residual obstructions
are of rather mundane technological nature encourages us to think that in the not-so-distant
future tests of Planck-scale in-vacuo dispersion in controlled laboratory experiments will be
possible.
). It is rather
optimistic to assume that the accuracy achieved in standard interferometers would also be
achievable with this peculiar setup, particularly since it would require the optics aspects of
the setup (such as lenses) to work with that high accuracy simultaneously with two beams of
different wavelength. Moreover, it would require some very smart techniques to vary the distance
between the frequency doublers without interfering with the effectiveness of the optics aspects
of the setup. So, in practice we would not presently be capable of using such setups to set
Planck-scale-sensitive limits on in-vacuo dispersion, but the fact that the residual obstructions
are of rather mundane technological nature encourages us to think that in the not-so-distant
future tests of Planck-scale in-vacuo dispersion in controlled laboratory experiments will be
possible.
Besides in-vacuo dispersion, another aspect of the physics of Planck-scale modified dispersion
relations that we should soon be able to test in controlled laboratory experiments is the one
concerning anomalous thresholds, at least in the case of the  process that I already
considered from an astrophysics perspective in Section 3.4. It is not so far from our present
technical capabilities to set up collisions between 10 TeV photons and 0.03 eV photons, thereby
reproducing essentially the situation of the analysis of blazars that I discussed in Section 3.4. And
notice that with respect to the analysis of observations of blazars, such controlled laboratory
studies would give much more powerful indications. In particular, for the analysis of observations
of blazars discussed in Section 3.4, a key limitation on our ability to translate the data into
experimental bounds on parameters of a pure-kinematics framework was due to the fact that (even
assuming we are indeed seeing absorption of multiTeV photons) the astrophysics context does
not allow us to firmly establish whether the absorption is indeed due to the IR component
of the intergalactic background radiation (as expected) or instead is due to a higher-energy
component of the background (in which case the absorption would instead be compatible with some
corresponding Planck-scale pictures). If collisions between 10 TeV and 0.03 eV photons in
the lab do produce pairs, since we would in that case have total control of the properties of
the particles in the in state of the process, we would then have firm pure-kinematics bounds
on the parameters of certain corresponding Planck scale test theories (such as the PKV0 test
theory).
process that I already
considered from an astrophysics perspective in Section 3.4. It is not so far from our present
technical capabilities to set up collisions between 10 TeV photons and 0.03 eV photons, thereby
reproducing essentially the situation of the analysis of blazars that I discussed in Section 3.4. And
notice that with respect to the analysis of observations of blazars, such controlled laboratory
studies would give much more powerful indications. In particular, for the analysis of observations
of blazars discussed in Section 3.4, a key limitation on our ability to translate the data into
experimental bounds on parameters of a pure-kinematics framework was due to the fact that (even
assuming we are indeed seeing absorption of multiTeV photons) the astrophysics context does
not allow us to firmly establish whether the absorption is indeed due to the IR component
of the intergalactic background radiation (as expected) or instead is due to a higher-energy
component of the background (in which case the absorption would instead be compatible with some
corresponding Planck-scale pictures). If collisions between 10 TeV and 0.03 eV photons in
the lab do produce pairs, since we would in that case have total control of the properties of
the particles in the in state of the process, we would then have firm pure-kinematics bounds
on the parameters of certain corresponding Planck scale test theories (such as the PKV0 test
theory).
These laboratory studies of Planck-scale-modified dispersion relations could also be adapted to the FTV0 test theory, by simply introducing some handles on the polarization of the photons that are placed under observation (also see Refs. [254, 255]), with sensitivity not far from Planck-scale sentivity in controlled laboratory experiments.
3.14 On test theories without energy-dependent modifications of dispersion relations
Readers for which this review is the first introduction to the world of quantum-spacetime phenomenology might be surprised that this long section, with an ambitious title announcing related tests of Lorentz symmetry, was so heavily biased toward probing the form of the energy-momentum dispersion relation. Other aspects of the implications of Lorentz (and Poincaré) symmetry did intervene, such as the law of energy-momentum conservation and its deformations (and the form of the interaction vertices and their deformations), and are in part probed through the data analyses reviewed, but the feature that clearly is at center stage is the structure of the dispersion relation. The reason for this is rather simple: researchers that recognize themselves as “quantum-spacetime phenomenologists” will consider a certain data analysis as part of the field if that analysis concerns an effect that can be robustly linked to quantum properties of spacetime (rather than, for example, some classical-field background) and if the analysis exposes the availability of Planck-scale sensitivities, in the sense I described above. At least according to the results obtained so far, the aspect of Lorentz/Poincaré symmetry that is most robustly challenged by the idea of a quantum spacetime is the form of the dispersion relation, and this is also an aspect of Lorentz/Poincaré symmetry for which the last decade of work on this phenomenology robustly exposed opportunities for Planck-scale sensitivities.
For the type of modifications of the dispersion relation that I considered in this section we have at present rather robust evidence of their applicability in certain noncommutative pictures of spacetime, where the noncommutativity is very clearly introduced at the Planck scale. And several independent (although all semi-heuristic) arguments suggest that the same general type of modified dispersion relations should apply to the “Minkowski limit” of LQG, a framework where a certain type of discretization of spacetime structure is introduced genuinely at the Planck scale. Unfortunately, these two frameworks are so complex that one does not manage to analyze spacetime symmetries much beyond building a “case” (and not a waterproof case) for modified dispersion relations.
A broader range of Lorentz-symmetry tests could be valuable for quantum-spacetime research,
but without the support of a derivation it is very hard to argue that the relevant effects are
being probed with sensitivities that are significant from a quantum-spacetime/Planck-scale
perspective. Think, for example, of a framework, such as the one adopted in Ref. [179], in
which the form of the dispersion relation is modified, but not in an energy-dependent way: one
still has dispersion relations of the type 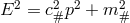 , but with a different value of the
velocity scale
, but with a different value of the
velocity scale 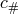 for different particles. This is not necessarily a picture beyond the realm of
possibilities one would consider from a quantum-spacetime perspective, but there is no known
quantum-spacetime picture that has provided direct support for it. And it is also essentially
impossible to estimate what accuracy must be achieved in measurements of
for different particles. This is not necessarily a picture beyond the realm of
possibilities one would consider from a quantum-spacetime perspective, but there is no known
quantum-spacetime picture that has provided direct support for it. And it is also essentially
impossible to estimate what accuracy must be achieved in measurements of  ,
in order to reach Planck-scale sensitivity. Some authors qualify as “Planckian magnitude” of
this type of effect, the case in which the dimensionless parameter has value on the order of
the ratio of the mass of the particles involved in the process versus the Planck scale (as in
,
in order to reach Planck-scale sensitivity. Some authors qualify as “Planckian magnitude” of
this type of effect, the case in which the dimensionless parameter has value on the order of
the ratio of the mass of the particles involved in the process versus the Planck scale (as in
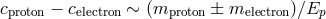 ) but this arbitrary criterion clearly does not amount to
establishing genuine Planck-scale sensitivity, at least as long as we do not have a derivation starting with
spacetime quantization at the Planck scale that actually finds such magnitudes of these sorts of
effects.
) but this arbitrary criterion clearly does not amount to
establishing genuine Planck-scale sensitivity, at least as long as we do not have a derivation starting with
spacetime quantization at the Planck scale that actually finds such magnitudes of these sorts of
effects.
Still, it is true that the general structure of the quantum-gravity problem and the structure of some of the quantum spacetimes that are being considered for the Minkowski limit of quantum gravity might host a rather wide range of departures from classical Lorentz symmetry. Correspondingly, a broad range of Lorentz-symmetry tests could be considered of potential interest.
I shall not review here this broader Lorentz-symmetry-tests literature, since it is not specific to
quantum-spacetime research (these are tests that could be done and in large part were done even before the
development of research on Lorentz symmetries from within the quantum-spacetime literature) and it has
already been reviewed very effectively in Ref. [395 ]. Let me just stress that for these broad searches of
departures from Lorentz symmetry one needs test theories with many parameters. Formalisms that
are well suited to a systematic program of such searches are already at an advanced stage of
development [180
]. Let me just stress that for these broad searches of
departures from Lorentz symmetry one needs test theories with many parameters. Formalisms that
are well suited to a systematic program of such searches are already at an advanced stage of
development [180 , 181
, 181 , 340
, 340 , 343
, 343 , 123
, 123 , 356
, 356 , 357
, 357 ] (also see Ref. [239]), and in particular the
“standard-model-extension” framework [180
] (also see Ref. [239]), and in particular the
“standard-model-extension” framework [180 , 181, 340
, 181, 340 , 343] has reached a high level of adoption of
preference for theorists and experimentalists as the language in which to characterize the results of
systematic multi-parameter Lorentz-symmetry-test data analyses. The “Standard Model Extension” was
originally conceived [340] as a generalization of the Standard Model of particle-physics interactions
restricted to power-counting-renormalizable correction terms, and as such it was of limited
interest for the bulk of the quantum-spacetime/quantum-gravity community: since quantum
gravity is not a (perturbatively) renormalizable theory, many quantum-spacetime researchers
would be unimpressed with Lorentz-symmetry tests restricted to powercounting-renormalizable
correction terms. However, over these last few years [123
, 343] has reached a high level of adoption of
preference for theorists and experimentalists as the language in which to characterize the results of
systematic multi-parameter Lorentz-symmetry-test data analyses. The “Standard Model Extension” was
originally conceived [340] as a generalization of the Standard Model of particle-physics interactions
restricted to power-counting-renormalizable correction terms, and as such it was of limited
interest for the bulk of the quantum-spacetime/quantum-gravity community: since quantum
gravity is not a (perturbatively) renormalizable theory, many quantum-spacetime researchers
would be unimpressed with Lorentz-symmetry tests restricted to powercounting-renormalizable
correction terms. However, over these last few years [123 ] most theorists involved in studies of the
“Standard Model Extension” have started to add correction terms that are not powercounting
renormalizable.26
A good entry point for the literature on limits on the parameters of the “Standard Model Extension” is
provided by Refs. [395
] most theorists involved in studies of the
“Standard Model Extension” have started to add correction terms that are not powercounting
renormalizable.26
A good entry point for the literature on limits on the parameters of the “Standard Model Extension” is
provided by Refs. [395 , 123, 346
, 123, 346 ].
].
From a quantum-gravity-phenomenology perspective it is useful to contemplate the differences between
alternative strategies for setting up a “completely general” systematic investigation of possible violations of
Lorentz symmetry. In particular, it has been stressed (see, e.g., Refs. [356 , 357
, 357 ]) that violations of Lorentz
symmetry can be introduced directly at the level of the dynamical equations, without assuming (as done in
the Standard Model Extension) the availability of a Lagrangian generating the dynamical equations. This is
more general than the Lagrangian approach: for example, the generalized Maxwell equation discussed in
Ref. [356
]) that violations of Lorentz
symmetry can be introduced directly at the level of the dynamical equations, without assuming (as done in
the Standard Model Extension) the availability of a Lagrangian generating the dynamical equations. This is
more general than the Lagrangian approach: for example, the generalized Maxwell equation discussed in
Ref. [356 , 357
, 357 ] predicts effects that go beyond the Standard Model Extension. And charge conservation,
which automatically comes from the Lagrangian approach, can be violated in models generalizing the field
equations [356, 357]. The comparison of the Standard-Model-Extension approach and of the
approach based on generalizations introduced directly at the level of the dynamical equations
illustrates how different “philosophies” lead to different strategies for setting up a “completely
general” systematic investigation of possible departures from Lorentz symmetry. By removing the
assumption of the availability of a Lagrangian, the second approach is “more general”. Still, no
“general approach” can be absolutely general: in principle one could always consider removing
an extra layer of assumptions. As the topics I have reviewed in this section illustrate, from a
quantum-spacetime-phenomenology perspective it is not necessarily appropriate to seek the most general
parametrizations. On the contrary, we would like to single out some particularly promising candidate
quantum-spacetime effects (as in the case of modified dispersion relations) and focus our efforts
accordingly.
] predicts effects that go beyond the Standard Model Extension. And charge conservation,
which automatically comes from the Lagrangian approach, can be violated in models generalizing the field
equations [356, 357]. The comparison of the Standard-Model-Extension approach and of the
approach based on generalizations introduced directly at the level of the dynamical equations
illustrates how different “philosophies” lead to different strategies for setting up a “completely
general” systematic investigation of possible departures from Lorentz symmetry. By removing the
assumption of the availability of a Lagrangian, the second approach is “more general”. Still, no
“general approach” can be absolutely general: in principle one could always consider removing
an extra layer of assumptions. As the topics I have reviewed in this section illustrate, from a
quantum-spacetime-phenomenology perspective it is not necessarily appropriate to seek the most general
parametrizations. On the contrary, we would like to single out some particularly promising candidate
quantum-spacetime effects (as in the case of modified dispersion relations) and focus our efforts
accordingly.



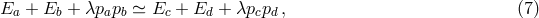
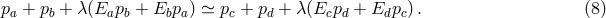








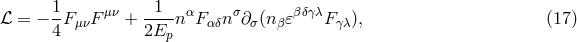
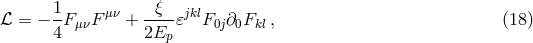


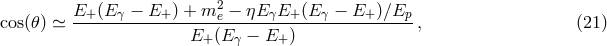





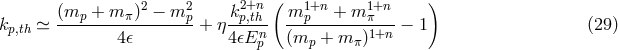
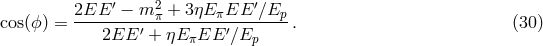


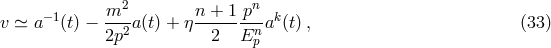
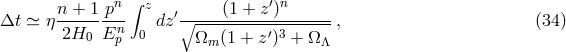
![1 Ec ≃ ---------------, (35 ) R ⋅ δ ⋅ [vγ − ve]](article423x.gif)