4 Other Areas of UV Quantum-Spacetime Phenomenology
Tests of Lorentz symmetry, and particularly of the form of the dispersion relation, probably make up something on the order of half of the whole quantum-spacetime-phenomenology literature. The other half is spread over a few other, evidently less developed, research lines. Nonetheless, for some of these other research lines the literature has reached some nonnegligible maturity, and even those that are at preliminary stages of development could be precious potential opportunities for quantum-spacetime research.Evidently, the most challenging part of this review work concerns these other components of quantum-spacetime-phenomenology research, since it is harder to summarize and organize intelligibly the results and scopes of research programs that are still in early stages of development. But it is also the part of this review that could be most valuable, since there is already some work [52, 308, 485, 294] attempting to summarize and review, although more concisely than done here in Section 3, the results obtained by the quantum-spacetime phenomenology of Planck-scale modified dispersion relations.
In reporting on the work done in these other quantum-spacetime-phenomenology reseach lines, I shall
use as one of the guiding concepts the one of assessing whether a given research program concerns UV
quantum-spacetime effects or IR quantum-spacetime effects. The typical situation for a UV
quantum-spacetime effect is that it takes the form of correction terms that grow with the energy of the
particles, and whose significance is therefore increasingly high as the energy of the particles increases. For
any given standard-physics (no-quantum-spacetime) prediction 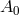 , this will take the general form
, this will take the general form
This is the type of quantum-spacetime effect that one traditionally one to be inevitably produced by any form of spacetime quantization, and is the focus of this section. The possibility of “IR quantum-spacetime effects”, effects that are due to Planck-scale spacetime quantization but are significant in some deep-IR regime, came to the attention of the community only rather recently, emerging mainly from work on “IR/UV mixing in quantum spacetime”, and I shall focus on it in the next Section 5.
4.1 Preliminary remarks on fuzziness
In this review, as natural for phenomenology, I am primarily looking at quantum-spacetime effects from the perspective of the type of pre-quantum-spacetime laws that they affect (so we have “departures from classical spacetime symmetries”, “violations of the quantum-mechanical coherence”, and so on). And our experimental opportunities are such that the main focus is on how spacetime quantization could affect particle propagation (and, for a restricted sample of phenomenological opportunities, interactions among particles). For this section on “other UV quantum-spacetime effects” a significant role (particularly noticeable in Sections 4.2, 4.3, and 4.5 will be played by the idea that quantum-spacetime effects may introduce an additional irreducible contribution to the fuzziness of the worldlines of particles.
This should be contrasted to the content of Section 3, which focuses mainly on phenomenological proposals involving mechanisms for systematic departures from the currently-adopted laws of propagation of (and interaction among) particles. In most cases such systematic effects amount to departures from the predictions of Lorentz symmetry (such as a systematic dependence on the velocity of a massless particle on its energy, which would produce a systematic difference between the arrival times of high-energy and low-energy photons that are simultaneously emitted).
If it ends up being the case that the correct quantum-spacetime picture does not provide us any such
systematic effects, then we will be left with non-systematic effects, i.e., “fuzziness” [57 ]. In looking for
such effects we can be guided by the intuition that spacetime quantization might act as an
environment inducing apparently random fluctuations in certain observables. For example, by distance
fuzziness one does not describe an effect that would systematically gives rise to larger (or smaller)
distance-measurement results, but rather one describes a sort of new uncertainty principle for distance
measurements.
]. In looking for
such effects we can be guided by the intuition that spacetime quantization might act as an
environment inducing apparently random fluctuations in certain observables. For example, by distance
fuzziness one does not describe an effect that would systematically gives rise to larger (or smaller)
distance-measurement results, but rather one describes a sort of new uncertainty principle for distance
measurements.
This distinction between systematic and nonsystematic effects can easily be characterized for any given
observable 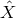 for which the pre-quantum-spacetime theoretical prediction can be described in terms of a
“prediction”
for which the pre-quantum-spacetime theoretical prediction can be described in terms of a
“prediction” 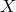 and, possibly, a fundamental (ordinarily quantum mechanical) “uncertainty”
and, possibly, a fundamental (ordinarily quantum mechanical) “uncertainty”
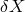 . The effects of spacetime quantization in general could lead [57
. The effects of spacetime quantization in general could lead [57 ] to a new prediction
] to a new prediction
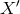 and a new uncertainty
and a new uncertainty 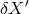 . One would attribute to quantum spacetime the effects
. One would attribute to quantum spacetime the effects
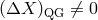 and
and 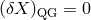 ,
while the opposite case,
,
while the opposite case, 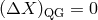 and
and 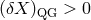 , can be qualified as purely non-systematic. It is
likely that for many observables both types of quantum-spacetime effect may be present simultaneously, but
it is natural that at least the first stages of development of a quantum-spacetime phenomenology on an
observable
, can be qualified as purely non-systematic. It is
likely that for many observables both types of quantum-spacetime effect may be present simultaneously, but
it is natural that at least the first stages of development of a quantum-spacetime phenomenology on an
observable 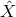 be focused on one or the other special case (
be focused on one or the other special case (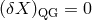 or
or 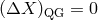 ).
Clearly, the discusions of effects given in Section 3 were all with
).
Clearly, the discusions of effects given in Section 3 were all with 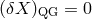 , while for most of
the proposals discussed in this section the main focus will be on the effects characterized by
, while for most of
the proposals discussed in this section the main focus will be on the effects characterized by
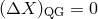 .
.
4.2 Spacetime foam, distance fuzziness and interferometric noise
The scenarios for spacetime fuzziness that are most studied from a quantum-spacetime perspective are intuitively linked to the notion of “spacetime foam”, championed by Wheeler and studied extensively in the quantum-gravity literature, more or less directly, for several decades (see, e.g., Refs. [547, 203, 178, 281, 150, 250, 553]). From a modern perspective one is attempting to characterize the physics of matter particles as effectively occurring in an “environment” of short-distance quantum-gravitational degrees of freedom. And one may expect that for propagating particles with wavelength much larger than the Planck length, when it may be appropriate to integrate out these short-distance quantum-gravitational degrees of freedom, the main residual effect of short-distance gravity would indeed be an additional contribution to the fuzziness of worldlines.
While in full-fledged quantum-spacetime theories, such a LQG, such analyses are still beyond our reach,
one can find partial encouragement for this intuition in recent progress on the understanding
of quantum gravity in 3D (2+1-dimensional) spacetime. Studies such as the ones reported in
Refs. [75 , 237
, 237 , 412, 152, 259
, 412, 152, 259 , 238
, 238 , 313, 441
, 313, 441 ] establish that for 3D quantum gravity (exploiting the much
lower complexity than for the 4D case) we are able to perform the task needed for studies of
spacetime foam: we can actually integrate out gravity, reabsorbing its effects into novel properties
for a gravity-free propagation of particles. And foaminess is formalized in the fact that this
procedure integrating out gravity leaves us with a theory of free particles in a noncommutative
spacetime, Refs. [75, 237, 259, 238
] establish that for 3D quantum gravity (exploiting the much
lower complexity than for the 4D case) we are able to perform the task needed for studies of
spacetime foam: we can actually integrate out gravity, reabsorbing its effects into novel properties
for a gravity-free propagation of particles. And foaminess is formalized in the fact that this
procedure integrating out gravity leaves us with a theory of free particles in a noncommutative
spacetime, Refs. [75, 237, 259, 238 ], specifically a spacetime with “Lie-algebra noncommutativity”
], specifically a spacetime with “Lie-algebra noncommutativity”
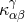 as the Levi-Civita tensor is the one suggested by the direct derivation
given in Ref. [441]). In other words, upon integrating out the gravitational degrees of freedom, the
quantum dynamics of matter fields coupled to 3D gravity is effectively described [238] by matter fields in a
noncommutative spacetime, a fuzzy/foamy spacetime.
as the Levi-Civita tensor is the one suggested by the direct derivation
given in Ref. [441]). In other words, upon integrating out the gravitational degrees of freedom, the
quantum dynamics of matter fields coupled to 3D gravity is effectively described [238] by matter fields in a
noncommutative spacetime, a fuzzy/foamy spacetime.
While the only direct/deductive derivations of such results are for 3D quantum gravity, it is natural to take that as a starting point for the study of real 4D quantum gravity, whereas analogous results are still unavailable. And a sizable literature has been devoted to the search of possible experimental manifestations of “spacetime foam”. Several subsections of this section concern related phenomenological proposals. I start with spacetime-foam test theories, whose structure renders them well suited for interferometric tests.
4.2.1 Spacetime foam as interferometric noise
The first challenge for a phenomenology investigating the possibility of spacetime foam originates in the fact that Wheeler’s spacetime foam intuition, while carrying strong conceptual appeal, cannot on its own be used for phenomenology, since it is not characterized in terms of observable properties. The phenomenology then is based on test theories inspired by the spacetime-foam intuition.
A physical/operative definition of at least one aspect of spacetime foam is
given in Refs. [51 , 54
, 54 , 53
, 53 , 433
, 433 ] and is well suited for a phenomenology based on
interferometry27.
According to this definition the fuzziness/foaminess of a spacetime is established[51
] and is well suited for a phenomenology based on
interferometry27.
According to this definition the fuzziness/foaminess of a spacetime is established[51 , 54
, 54 , 53
, 53 , 433
, 433 ] on the basis of an analysis
of strain noise28
in interferometers set up in that spacetime. In achieving their remarkable accuracy, modern interferometers
must deal with several classical-physics strain noise sources (e.g., thermal and seismic effects induce
fluctuations in the relative positions of the test masses). And importantly strain noise sources associated
with effects due to ordinary quantum mechanics are also significant for modern interferometers (the
combined minimization of photon shot noise and radiation pressure noise leads to a noise source that
originates from ordinary quantum mechanics [486
] on the basis of an analysis
of strain noise28
in interferometers set up in that spacetime. In achieving their remarkable accuracy, modern interferometers
must deal with several classical-physics strain noise sources (e.g., thermal and seismic effects induce
fluctuations in the relative positions of the test masses). And importantly strain noise sources associated
with effects due to ordinary quantum mechanics are also significant for modern interferometers (the
combined minimization of photon shot noise and radiation pressure noise leads to a noise source that
originates from ordinary quantum mechanics [486 ]). One can give an operative definition [51
]). One can give an operative definition [51 , 53
, 53 ] of
fuzzy/foamy spacetime in terms of a corresponding additional source of strain noise. A theory in which the
concept of distance is fundamentally fuzzy in this operative sense would be such that the read-out of an
interferometer would still be noisy (because of quantum-spacetime effects) even in the idealized limit
in which all classical-physics and ordinary-quantum-mechanics noise sources are completely
eliminated/subtracted.
] of
fuzzy/foamy spacetime in terms of a corresponding additional source of strain noise. A theory in which the
concept of distance is fundamentally fuzzy in this operative sense would be such that the read-out of an
interferometer would still be noisy (because of quantum-spacetime effects) even in the idealized limit
in which all classical-physics and ordinary-quantum-mechanics noise sources are completely
eliminated/subtracted.
4.2.2 A crude estimate for laser-light interferometers
Before even facing the task of developing test theories for spacetime foaminess in interferometry it is best to
first check whether there is any chance of using realistic interferometric setups to uncover effects as small as
expected if introduced at the Planck scale. A first encouraging indication comes from identifying the
presence of a huge amplifier in modern interferometers: a well-known quality of these modern
interferometers is their ability to detect gravity waves of amplitude 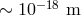 by carefully monitoring
distances of order
by carefully monitoring
distances of order 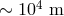 , and this should provide opportunities for an “amplifier” that is of order
, and this should provide opportunities for an “amplifier” that is of order
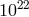 .
.
This also means that our modern interferometers have outstanding control over noise sources,
which is ideal for the task at hand, involving scenarios for how quantum-spacetime effects may
contribute an additional source of noise in such interferometers. Clearly, the noise we could
conceivably see emerging from spacetime quantization should be modeled in terms of some
random vibrations. Evidently random vibrations are particularly difficult to characterize. For
example there is in general no spendable notion of “amplitude” of random vibrations. The
most fruitful way to characterize them, also for the purposes of comparing their “intensity” to
other non-random sources of vibration that might affect the same system, is by using the power
spectral density. Let me introduce some notation, which will prove useful when I move on to
discuss crude models of quantum-spacetime-induced noise. For this I simple-mindedly consider
the readout of an interferometer as 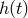 , given by the position
, given by the position 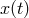 of a mirror divided
by a reference length scale
of a mirror divided
by a reference length scale 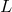 (
(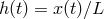 ), and adjust the reference frame so that on
average
), and adjust the reference frame so that on
average 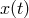 vanishes,
vanishes,  . Given some rules for fluctuations of this readout one can
indeed be interested in its power spectral density
. Given some rules for fluctuations of this readout one can
indeed be interested in its power spectral density 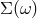 , in principle computable via [486
, in principle computable via [486 ]
]
![μ[h(t)h(t+ τ)]](article506x.gif) depends only on
depends only on 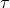 and is the value expected on average for
and is the value expected on average for 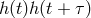 in the
presence of the vibration/fluctuation process of interest in the analysis.
in the
presence of the vibration/fluctuation process of interest in the analysis.
Having characterized the noise source in terms of its power spectral density we can then easily compute
some primary characteristics, such as its root mean square deviation 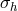 , which for cases of zero-mean
noise, such as the one I am considering, will be given by the expectation of
, which for cases of zero-mean
noise, such as the one I am considering, will be given by the expectation of 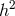 . This can be expressed in
terms of the power spectral density as follows [486]
. This can be expressed in
terms of the power spectral density as follows [486]
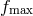 ) and a finite observation time (
) and a finite observation time (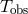 ),
this relation will take the shape
),
this relation will take the shape
In modern interferometers such as LIGO [9 , 1
, 1 ] and VIRGO [157
] and VIRGO [157 , 12
, 12 ] the power spectral density of the
noise is controlled at a level of
] the power spectral density of the
noise is controlled at a level of 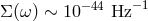 at observation frequencies
at observation frequencies 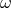 of about
100 Hz, and in turn this (also considering the length of the arms of these modern interferometers)
implies [9, 1, 157, 12] that for a gravity wave with 100 Hz frequency the detection threshold is indeed
around
of about
100 Hz, and in turn this (also considering the length of the arms of these modern interferometers)
implies [9, 1, 157, 12] that for a gravity wave with 100 Hz frequency the detection threshold is indeed
around 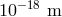 .
.
The challenge here for quantum-spacetime phenomenologists is to characterize the relevant
quantum-spacetime effects in terms of a novel contribution ![[QG ] Σ (ω )](article518x.gif) to the power spectral density of the
noise. If at some point experimentalists manage to bring the total noise
to the power spectral density of the
noise. If at some point experimentalists manage to bring the total noise 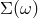 , for some range of
observation frequencies
, for some range of
observation frequencies 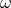 , below the level predicted by a certain quantum-spacetime test theory, then
that test theory will be ruled out.
, below the level predicted by a certain quantum-spacetime test theory, then
that test theory will be ruled out.
Is there any hope for a reasonable quantum-spacetime test theory to predict noise at a level comparable to the ones that are within the reach of modern interferometry? Well, this is the type of question that one can only properly address in the context of models, but it may be valuable to first use dimensional analysis, assuming the most optimistic behavior of the quantum-spacetime effects, and check if the relevant order of magnitude is at all providing any encouragement for the painful (if at all doable) analysis of the relevant issues in quantum-spacetime models.
To get what is likely to be the most optimistic (and certainly the simplest, but not necessarily the most
realistic) Planck-scale estimate of the effect, let us assume that quantum-spacetime noise is
“white noise”,  = Σ 0](article521x.gif) (frequency independent), so that it is fully specified by a single
dimensionful number setting the level of this white noise. And since
(frequency independent), so that it is fully specified by a single
dimensionful number setting the level of this white noise. And since 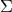 carries units of
carries units of 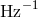 one
easily notices [54
one
easily notices [54 ] a tempting simple naive estimate in terms of the Planck length and the
speed-of-light29
scale:
] a tempting simple naive estimate in terms of the Planck length and the
speed-of-light29
scale: 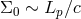 , which, since
, which, since 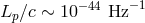 , encouragingly happens to be just at the mentioned
level of sensitivity of LIGO-VIRGO-type interferometers. This provides some initial encouragement for a
phenomenology based on interferometric noise, though only within the limitations of a very crude and naive
estimate.
, encouragingly happens to be just at the mentioned
level of sensitivity of LIGO-VIRGO-type interferometers. This provides some initial encouragement for a
phenomenology based on interferometric noise, though only within the limitations of a very crude and naive
estimate.
4.2.3 A simple-minded mechanism for noise in laser-light interferometers
My next task is going beyond assuming for simplicity that the quantum-spacetime noise be white and beyond adopting a naive dimensional-analysis estimate of what could constitute a Planck-scale level of such a noise. The ultimate objective here would be to analyze an interferometer in the framework of a compelling quantum-spacetime theory, but this is beyond our capabilities at present. However, we can start things off by identifying some semi-heuristic pictures (the basis for a test theory) with effects introduced genuinely at the Planck scale that turn out to produce strain noise at the level accessible with modern interferometers.
Having in mind this objective, let us take as a starting point for a first naive picture of spacetime
fuzziness the popular arguments suggesting that the Planck scale should also set some absolute limitation
on the measurability of distances. And let us (optimistically) assume that this translates to the fact that
any experiment in which a distance 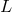 plays a key role (meaning that one is either measuring
plays a key role (meaning that one is either measuring 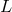 itself or
the observable quantity under study depends strongly on
itself or
the observable quantity under study depends strongly on 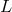 ) is affected by a mean square deviation
) is affected by a mean square deviation
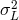 .
.
It turns out to be useful [51 , 53
, 53 ] to consider this
] to consider this 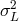 as a possible stepping stone toward the
strain-noise power-spectrum estimate. And a particularly striking picture arises by assuming that the
distances
as a possible stepping stone toward the
strain-noise power-spectrum estimate. And a particularly striking picture arises by assuming that the
distances 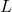 between the test masses of an interferometer be affected by Planck-length fluctuations of
random-walk type occurring at a rate of one per Planck time (
between the test masses of an interferometer be affected by Planck-length fluctuations of
random-walk type occurring at a rate of one per Planck time (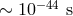 ), so that [51
), so that [51 , 53
, 53 ]
]
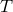 is the time scale over which the experiment monitors the distance
is the time scale over which the experiment monitors the distance 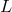 , assuming the use of
ultrarelativistic particles (
, assuming the use of
ultrarelativistic particles (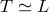 ).
).
It is noteworthy that 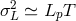 can be motivated independently (without having in mind the idea of
such effective spacetime fluctuations) on the basis of some aspects of the quantum-gravity problem [50].
And the study of certain quantum-spacetime pictures that have been of interest to the quantum-gravity
community, such as the
can be motivated independently (without having in mind the idea of
such effective spacetime fluctuations) on the basis of some aspects of the quantum-gravity problem [50].
And the study of certain quantum-spacetime pictures that have been of interest to the quantum-gravity
community, such as the  -Minkowski noncommutative spacetime of Eq. (4
-Minkowski noncommutative spacetime of Eq. (4 ), provide some support for
this random-walk picture: from
), provide some support for
this random-walk picture: from ![[xj, t] = iLP xj](article542x.gif) one could guess roughly a law of the form
one could guess roughly a law of the form
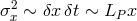 .
.
Some arguments inspired by the “holography paradigm” for quantum gravity [433 , 430
, 430 , 170
, 170 ] suggest
even weaker effects, characterized by
] suggest
even weaker effects, characterized by
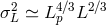 had been independently proposed in the quantum-gravity
literature on the basis of a perspective on the quantum-gravity problem (see Ref. [432, 319, 209]), which
originally in no way involved spacetime fuzziness.
had been independently proposed in the quantum-gravity
literature on the basis of a perspective on the quantum-gravity problem (see Ref. [432, 319, 209]), which
originally in no way involved spacetime fuzziness.
Probably the most conservative (and pessimistic) expectation for spacetime fuzziness one can find in the quantum-spacetime literature is the one omitting any opportunity for amplification by the involvement of a long observation time (see, e.g., parts of Refs. [249, 293])
The random-walk case is the most typical textbook study case for random noise. Its power spectral
density goes like 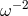 , so one should have
, so one should have
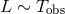 one indeed finds
one indeed finds 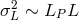 ).
).
Analogously, one can associate to the “holographic noise” of Eq. (45 ) a power spectral density going as
) a power spectral density going as
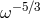 , so one should have
, so one should have
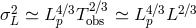 .
.
And, finally, for the 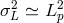 case of Eq. (46
case of Eq. (46 ), a rough but valuable approximate description of the
power spectral density goes like
), a rough but valuable approximate description of the
power spectral density goes like 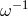 , so one should have
, so one should have
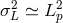 .
.
It is tempting to obtain from these estimates of the quantum-spacetime-induced distance uncertainty an
estimate for the quantum-spacetime-induced strain noise, by simply dividing by the square of the length of
the arms of the interferometer, ![Σ [QG ] = Σ [QG ]∕L2 L](article559x.gif) . This would be the way to proceed if we were converting
distance noise into strain noise, but really here we are obtaining a rough estimate of strain noise from an
estimate of distance uncertainty, and I shall therefore proceed in some sense sub judice (see in particular my
comments below concerning the large number of photons collectively used for producing the accurate
measurements of a modern interferometer). Assuming that indeed
. This would be the way to proceed if we were converting
distance noise into strain noise, but really here we are obtaining a rough estimate of strain noise from an
estimate of distance uncertainty, and I shall therefore proceed in some sense sub judice (see in particular my
comments below concerning the large number of photons collectively used for producing the accurate
measurements of a modern interferometer). Assuming that indeed ![Σ[QG] = Σ[QG]∕L2 L](article560x.gif) , and taking as
reference value an observation frequency of
, and taking as
reference value an observation frequency of 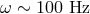 , one would get for the three cases I
discussed the following estimates of strain noise at 100 Hz, for arm lengths of a few kilometers:
, one would get for the three cases I
discussed the following estimates of strain noise at 100 Hz, for arm lengths of a few kilometers:
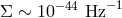 , so estimates like
, so estimates like ![Σ[QG;weak]](article564x.gif) and
and ![Σ [QG;holo]](article565x.gif) would
be safe, but the estimate
would
be safe, but the estimate ![Σ [QG;rw]](article566x.gif) must be excluded: the estimate
must be excluded: the estimate ![Σ[QG;rw]](article567x.gif) would assign more noise of
quantum-spacetime origin than the total noise that LIGO and VIRGO managed to control (which would
include the hypothetical quantum-spacetime-induced noise). In spite of the crudeness of the derivations I
discussed so far, this does give a rather worthy input for those who fancy the random-walk picture, as I
shall stress in Section 4.2.4.
would assign more noise of
quantum-spacetime origin than the total noise that LIGO and VIRGO managed to control (which would
include the hypothetical quantum-spacetime-induced noise). In spite of the crudeness of the derivations I
discussed so far, this does give a rather worthy input for those who fancy the random-walk picture, as I
shall stress in Section 4.2.4.
Before I get to that issue, let me stress that there is a possible source of confusion for terminology (and
content) in the literature. In the quantum-gravity literature there has been some discussion for several years
of “holography-inspired noise” in the sense of my Eq. (49 ) and of Refs. [433
) and of Refs. [433 , 430
, 430 , 170
, 170 ]. More recently, a
different mechanism for quantum-spacetime-induced noise, also labeled as “holography inspired”, was
proposed in a series of papers by Hogan [287
]. More recently, a
different mechanism for quantum-spacetime-induced noise, also labeled as “holography inspired”, was
proposed in a series of papers by Hogan [287 , 286
, 286 , 288
, 288 ]. There is no relation between the two
“holography-inspired” proposals for quantum-spacetime-induced interferometric noise. I do not think it is
particularly important at the present time to establish which (if either) of the two proposals is more directly
inspired by holography. I must instead stress that the holographic noise of Refs. [433
]. There is no relation between the two
“holography-inspired” proposals for quantum-spacetime-induced interferometric noise. I do not think it is
particularly important at the present time to establish which (if either) of the two proposals is more directly
inspired by holography. I must instead stress that the holographic noise of Refs. [433 , 430, 170
, 430, 170 ] is a rather
mature proposal, centered on Eq. (49
] is a rather
mature proposal, centered on Eq. (49 ) and meaningful at least as a quantum-spacetime test theory
in the sense I just described. Instead it is probably fair to describe the alternative version of
holographic noise more recently proposed in Ref. [287, 286
) and meaningful at least as a quantum-spacetime test theory
in the sense I just described. Instead it is probably fair to describe the alternative version of
holographic noise more recently proposed in Ref. [287, 286 , 288
, 288 ] as a young proposal still
looking for some maturity: it does not amount to any however-wild variant of the description of
interferometric noise I summarized here, and actually it is claimed [288
] as a young proposal still
looking for some maturity: it does not amount to any however-wild variant of the description of
interferometric noise I summarized here, and actually it is claimed [288 ] to be immune not
only to the sort of interferometric noise I discussed in this Section but also to all other effects
that have been typically associated with spacetime quantization in the literature. It would
be a quantum-spacetime picture whose effects “can only be detected in an experiment that
coherently compares transverse positions over an extended spacetime volume to extremely high
precision, and with high time resolution or bandwidth” [288] . Evidently some work is still
needed on the conceptual aspects (as a rigorous theory of spacetime quantization) and on the
phenomenological aspects (as a computably predictive and broadly applicable test theory of spacetime
quantization) of this proposal. Only time will tell if this present lack of maturity is due to intrinsic
unsurmountable limitations of the proposal or is simply a result of the fact that the proposal was made
only rather recently (so there was not much time for this maturity to be reached). I should
note that at some point, in spite of its lack of maturity, this proposal started to attract some
pronounced interest in relation to reports by the GEO600 interferometer [550] of unexplained
excess noise [373]: it had been claimed [286] that Hogan’s version of holographic noise could
match exactly the anomaly that was being reported by GEO600. However, it appears that
experimenters at GEO600 have recently achieved a better understanding of their noise sources, and no
unexplained contribution is at this point reported (this is at least implicit in Ref. [462] and is
highlighted at
] to be immune not
only to the sort of interferometric noise I discussed in this Section but also to all other effects
that have been typically associated with spacetime quantization in the literature. It would
be a quantum-spacetime picture whose effects “can only be detected in an experiment that
coherently compares transverse positions over an extended spacetime volume to extremely high
precision, and with high time resolution or bandwidth” [288] . Evidently some work is still
needed on the conceptual aspects (as a rigorous theory of spacetime quantization) and on the
phenomenological aspects (as a computably predictive and broadly applicable test theory of spacetime
quantization) of this proposal. Only time will tell if this present lack of maturity is due to intrinsic
unsurmountable limitations of the proposal or is simply a result of the fact that the proposal was made
only rather recently (so there was not much time for this maturity to be reached). I should
note that at some point, in spite of its lack of maturity, this proposal started to attract some
pronounced interest in relation to reports by the GEO600 interferometer [550] of unexplained
excess noise [373]: it had been claimed [286] that Hogan’s version of holographic noise could
match exactly the anomaly that was being reported by GEO600. However, it appears that
experimenters at GEO600 have recently achieved a better understanding of their noise sources, and no
unexplained contribution is at this point reported (this is at least implicit in Ref. [462] and is
highlighted at  http://www.aei.mpg.de/hannover-en/05-research/GEO600/). The brief season of
the “GEO600 anomaly” (at some point known among specialists as the “mystery noise”) is
over.
http://www.aei.mpg.de/hannover-en/05-research/GEO600/). The brief season of
the “GEO600 anomaly” (at some point known among specialists as the “mystery noise”) is
over.
4.2.4 Insight already gained and ways to go beyond it
At the present time the “state of the art” of phenomenologically-spendable descriptions of
Planck-scale-induced strain noise does not go much beyond the simple-minded estimates I just described in
relation to Eqs. (47 ), (49
), (49 ), and (50
), and (50 ). But some lessons were nonetheless learned, as usually happens even
with the most humble phenomenology. And these lessons do point toward some directions worthy of
exploration in the future. In this section I highlight some of these lessons and possible future
developments.
). But some lessons were nonetheless learned, as usually happens even
with the most humble phenomenology. And these lessons do point toward some directions worthy of
exploration in the future. In this section I highlight some of these lessons and possible future
developments.
Among the few steps of simple derivation, which I described in Section 4.2.3, evidently much scrutiny
should be particularly directed toward the assumption ![[QG ] [QG ] 2 Σ = Σ L ∕L](article568x.gif) : I motivated some candidate
forms for
: I motivated some candidate
forms for ![Σ[LQG]](article569x.gif) using essentially the sort of arguments that usually allow us to establish uncertainty
principles for single particles, such as the ones taking as a starting point a postulated noncommutativity of
single-particle coordinates; however, the strain noise
using essentially the sort of arguments that usually allow us to establish uncertainty
principles for single particles, such as the ones taking as a starting point a postulated noncommutativity of
single-particle coordinates; however, the strain noise ![[QG] Σ](article570x.gif) relevant for our interferometers is not at all a
single-particle feature. Let me use the example of random-walk fuzziness for illustrating how the
relationship between single-particle quantum-spacetime arguments and interferometric strain noise
could be more subtle than assumed in
relevant for our interferometers is not at all a
single-particle feature. Let me use the example of random-walk fuzziness for illustrating how the
relationship between single-particle quantum-spacetime arguments and interferometric strain noise
could be more subtle than assumed in ![[QG] [QG] 2 Σ = ΣL ∕L](article571x.gif) . For this, I shall follow Ref. [57
. For this, I shall follow Ref. [57 ] (a
similar thesis was also reported in Ref. [170]). I specialize the more general idea of random-walk
quantum-spacetime fuzziness in the sense of assuming that each single photon in an interferometer
experiences a random-walk path: a random Planck-length fluctuation per Planck-time would
affect the path of each photon of the beam. This would imply in particular that as a photon
goes from one mirror of the interferometer to the other, over a distance
] (a
similar thesis was also reported in Ref. [170]). I specialize the more general idea of random-walk
quantum-spacetime fuzziness in the sense of assuming that each single photon in an interferometer
experiences a random-walk path: a random Planck-length fluctuation per Planck-time would
affect the path of each photon of the beam. This would imply in particular that as a photon
goes from one mirror of the interferometer to the other, over a distance 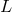 , it reaches its
destination with an uncertainty corresponding to
, it reaches its
destination with an uncertainty corresponding to 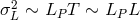 . However, the interferometer
(and this is key to its outstanding sensitivity) does not depend on determining the position of
each single photon in the beam: on the contrary the key observable is the average position
of the photons composing the beam, which may be viewed as the putative “position of the
mirror” (when such a beam reaches the mirror). If
. However, the interferometer
(and this is key to its outstanding sensitivity) does not depend on determining the position of
each single photon in the beam: on the contrary the key observable is the average position
of the photons composing the beam, which may be viewed as the putative “position of the
mirror” (when such a beam reaches the mirror). If 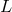 is now viewed as the distance between
positions of mirrors defined in this way, rather than as the distance of propagation of an individual
photon, then evidently the result is an estimate
is now viewed as the distance between
positions of mirrors defined in this way, rather than as the distance of propagation of an individual
photon, then evidently the result is an estimate 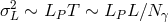 , where
, where 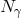 is the
(very large!) number of photons contributing to each such determination of the “position of the
mirror”.
is the
(very large!) number of photons contributing to each such determination of the “position of the
mirror”.
While the noise levels produced by a random-walk ansatz assuming ![[QG ] [QG ] 2 Σ = Σ L ∕L](article577x.gif) are, as stressed
in Section 4.2.3, already ruled out by the achievements of LIGO and VIRGO, this single-particle picture of
a random-walk scenario, which evidently leads us to assume
are, as stressed
in Section 4.2.3, already ruled out by the achievements of LIGO and VIRGO, this single-particle picture of
a random-walk scenario, which evidently leads us to assume
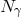 suppression.
suppression.
This observation is not specific to the random-walk scenario. A similar 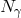 suppression
could naturally be expected for the holographic noise scenario of Eq. (49
suppression
could naturally be expected for the holographic noise scenario of Eq. (49 ). As discussed in
the previous Section 4.2.3, that holographic noise scenario would be safe from LIGO/VIRGO
bounds even without the
). As discussed in
the previous Section 4.2.3, that holographic noise scenario would be safe from LIGO/VIRGO
bounds even without the 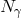 suppression. (In some sense that holographic noise scenario
would turn into unpleasantly “too safe from LIGO/VIRGO”, i.e., probably beyond the reach of
any foreseeable interferometric experiment, if it were to take into account the plausible
suppression. (In some sense that holographic noise scenario
would turn into unpleasantly “too safe from LIGO/VIRGO”, i.e., probably beyond the reach of
any foreseeable interferometric experiment, if it were to take into account the plausible 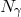 suppression).
suppression).
Concerning the scenario for weak quantum-spacetime-induced fuzziness, the one of Eq. (50 ),
contemplating the possibility of an
),
contemplating the possibility of an 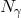 suppression is of mere academic interest: those noise levels are so
low, even without the possible additional
suppression is of mere academic interest: those noise levels are so
low, even without the possible additional 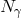 suppression, that we should exclude their testability for the
foreseeable future.
suppression, that we should exclude their testability for the
foreseeable future.
But for random-walk noise and for the holographic-noise scenario of Eq. (49 ) this issue of a
possible
) this issue of a
possible 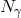 suppression needs to be investigated and understood. This is probably not for the
LIGO/VIRGO season: LIGO and VIRGO have not found any excess noise so far, and at this point
it is unlikely they will ever find it. But a completely new drawing board for phenomenology
would materialize with the advent of LISA [282]: LISA will operate at lower observational
frequencies
suppression needs to be investigated and understood. This is probably not for the
LIGO/VIRGO season: LIGO and VIRGO have not found any excess noise so far, and at this point
it is unlikely they will ever find it. But a completely new drawing board for phenomenology
would materialize with the advent of LISA [282]: LISA will operate at lower observational
frequencies 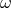 than LIGO/VIRGO-type interferometers, which is important from the
quantum-spacetime perspective since both random-walk noise, as described by Eq. (47
than LIGO/VIRGO-type interferometers, which is important from the
quantum-spacetime perspective since both random-walk noise, as described by Eq. (47 ), and
the holographic-noise scenario of Eq. (49
), and
the holographic-noise scenario of Eq. (49 ) predict effects that increase at lower observational
frequencies.30
The outcome of such LISA quantum-spacetime-noise studies may then depend on issues such as the possible
) predict effects that increase at lower observational
frequencies.30
The outcome of such LISA quantum-spacetime-noise studies may then depend on issues such as the possible
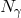 suppression.
suppression.
I should also stress that the analysis of these opportunities for quantum-spacetime phenomenology from
experiments operating at low observational frequencies 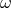 , is perhaps the most significant and
most robust conceptual achievement of the sort of phenomenology of spacetime foam that I am
discussing in this Section. When these pictures were first proposed it was seen by many as a total
surprise that one could contemplate Planck-scale effects at frequencies of observation of only
100 Hz. The naive argument goes something like “Planck-scale-induced noise must be studied
at Planck frequency”, and the Planck frequency is
, is perhaps the most significant and
most robust conceptual achievement of the sort of phenomenology of spacetime foam that I am
discussing in this Section. When these pictures were first proposed it was seen by many as a total
surprise that one could contemplate Planck-scale effects at frequencies of observation of only
100 Hz. The naive argument goes something like “Planck-scale-induced noise must be studied
at Planck frequency”, and the Planck frequency is 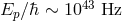 . However, in analyzing
actual pictures of quantum-spacetime fuzziness, even the simple-minded ones described above,
one becomes familiar with well-known facts establishing (and we should expect this lesson to
apply even to more sophisticated picture of quantum-spacetime-induced fuzziness) that discrete
fluctuation mechanisms tend to produce very significant effects at low observational frequencies
. However, in analyzing
actual pictures of quantum-spacetime fuzziness, even the simple-minded ones described above,
one becomes familiar with well-known facts establishing (and we should expect this lesson to
apply even to more sophisticated picture of quantum-spacetime-induced fuzziness) that discrete
fluctuation mechanisms tend to produce very significant effects at low observational frequencies
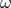 , with typical behaviors of the type
, with typical behaviors of the type 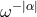 , even when their charateristic time scale is
ultrashort.
, even when their charateristic time scale is
ultrashort.
4.2.5 Distance fuzzyness for atom interferometers
Since the phenomenology of the implications of spacetime foam for interferometry is at an early stage of development, at the present time it may be premature to enter into detailed discussions of what type of interferometry might be best suited for uncovering quantum-spacetime/Planck-scale effects. Accordingly, in Section 4.2 I focus by default on the simplest case of interferometric studies, the one using a laser-light beam. However, in recent times atom interferometry has reached equally astonishing levels of sensitivity and for several interferometric measurements it is presently the best choice. Laser-light interferometry is still preferred for certain well-established techniques of interferometric studies of spacetime observables, as in the case of searches for gravity waves, and the observations I reported above for the phenomenology of strain noise induced by quantum-spacetime effects appear to be closely linked to the issues encountered in the search for gravity waves. However, it seems plausible that soon there will be some atom-interferometry setups that are competitive for gravity-wave searches (see, e.g., Refs. [526, 208]). This in turn might imply that searches of quantum-spacetime-induced strain noise could rely on atom interferometry.
The alternative between light and matter interferometry might prove valuable at later more mature stages of this phenomenology. It is likely that different test theories will give different indications in this respect, so that atom interferometry might provide the tightest constraints on some spacetime-foam test theories, whereas laser-light interferometry might provide the best constraints on other spacetime-foam test theories. A key aspect of the description of Planck-scale effects for atom interferometry to be addressed by the test theories (and hopefully, some day, by some fully-developed quantum-spacetime/quantum-gravity theories) is the role played by the mass of the atoms. With respect to laser-light interferometry, the case of atom interferometry challenges us with at least two more variables to be controlled at the theory level, which are the mass of the atoms and their compositeness. How do these two aspects of atom interferometry interface with the quantum-spacetime features that are of interest here? Do they effectively turn out to introduce suppressions of the relevant effects or on the contrary could they be exploited to see the effects? For none of the quantum-spacetime models that are presently studied have we reached a level of understanding of physical implications robust enough for us to answer confidently these questions. Perhaps we should also worry about (or exploit) another feature that is in principle tunable in atom interferometry, which is the velocity of the particles in the beam.
4.3 Fuzziness for waves propagating over cosmological distances
Interferometric studies of spacetime-foam are another rare example of tests of quantum-spacetime effects that can be conducted in a controlled laboratory setup (also see Section 3.13). Astrophysics may turn into the most powerful arena for this type of study. Indeed, the studies I discussed in the previous Section 4.2, which started toward the end of the 1990s, inspired a few years later some follow-up studies from the astrophysics side. As should be expected, the main opportunities come from observations of waves that have propagated over very large distances, thereby possibly accumulating a significant collective effect of the fuzziness encountered along the way to our detectors.
4.3.1 Time spreading of signals
An implication of distance fuzziness that one should naturally consider for waves propagating over large
distances is the possibility of “time spreading” of the signal: if at the source the signal only lasted a certain
very short time, but the photons that compose the signal travel a large distance 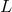 , affected by
uncertainty
, affected by
uncertainty 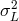 , before reaching our detectors the observed spread of times of arrival might
carry little trace of the original time spread at the source and be instead a manifestation of the
quantum-gravity-induced
, before reaching our detectors the observed spread of times of arrival might
carry little trace of the original time spread at the source and be instead a manifestation of the
quantum-gravity-induced 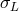 . If the distance
. If the distance 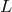 is affected by a quantum-spacetime uncertainty
is affected by a quantum-spacetime uncertainty
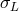 then different photons composing the signal will effectively travel distances that are not
all exactly given by
then different photons composing the signal will effectively travel distances that are not
all exactly given by 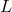 but actually differ from
but actually differ from 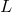 and from each other up to an amount
and from each other up to an amount
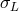 .
.
Again, it is of particular interest to test laws of the type discussed in the previous Section 4.2, but
it appears that these effects would be unobservably small even in the case that provides the
strongest effects, which is the random-walk ansatz 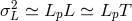 (assuming ultrarelativistic
particles, for which
(assuming ultrarelativistic
particles, for which 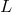 is at least roughly equal to the time duration
is at least roughly equal to the time duration 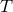 of the journey).
To see this let me consider once again gamma-ray bursts, which often travel for times on the
order of
of the journey).
To see this let me consider once again gamma-ray bursts, which often travel for times on the
order of 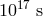 before reaching Earth detectors and are sometimes characterized by time
structures (microbursts within the burst) that have durations as short as
before reaching Earth detectors and are sometimes characterized by time
structures (microbursts within the burst) that have durations as short as 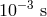 . Values of
. Values of 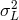 as small as
as small as 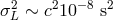 could be noticeable in the analysis of such bursts. However, the
estimate
could be noticeable in the analysis of such bursts. However, the
estimate 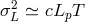 only provides
only provides 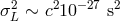 and is, therefore, much beyond our
reach.
and is, therefore, much beyond our
reach.
I shall comment in Section 4.8 on an alternative formulation of the phenomenology of
quantum-spacetime-induced worldline fuzziness, the one in Ref. [490 ] inspired by the causal-set approach
(the approach on which Section 4.8 focuses).
] inspired by the causal-set approach
(the approach on which Section 4.8 focuses).
4.3.2 Fuzziness from nonsystematic symmetry-modification effects
As an alternative way to model spacetime fuzziness, there has been some interest [431 , 72
, 72 , 37
, 37 ] in the
possibility that there might be effects resembling the ones discussed in Section 3, which are systematic
deviations from the predictions of Poincaré symmetry, but are “nonsystematic” in the sense discussed at
the beginning of this section. The possibility of fuzziness of particle worldlines governed by
] in the
possibility that there might be effects resembling the ones discussed in Section 3, which are systematic
deviations from the predictions of Poincaré symmetry, but are “nonsystematic” in the sense discussed at
the beginning of this section. The possibility of fuzziness of particle worldlines governed by 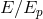 ,
mentioned in the previous Section 4.3.1, is an example of such nonsystematic violations of Poincaré
symmetry.
,
mentioned in the previous Section 4.3.1, is an example of such nonsystematic violations of Poincaré
symmetry.
These speculations are not on firm ground on the theory side, in the sense that there is not much in
support of this among available results on actual analysis of formalizations of spacetime quantization. But it
is legitimate to expect that this might be due to our limited abilities in mastering these complex formalisms.
After all, as suggested in Ref. [431 ], if spacetime geometry is fuzzy then it may be inevitable for the
operative procedures that give sense to the notion of energy and momentum of a particle to also be
fuzzy.
], if spacetime geometry is fuzzy then it may be inevitable for the
operative procedures that give sense to the notion of energy and momentum of a particle to also be
fuzzy.
This sort of picture could have tangible observational consequences. For example, it can inspire, as
suggested in Refs. [74 , 57
, 57 , 72
, 72 ], scenarios such that spacetime fuzziness effectively produces an uncertainty
in the velocity of particles of order
], scenarios such that spacetime fuzziness effectively produces an uncertainty
in the velocity of particles of order 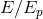 . This would give rise to a magnitude of these nonsystematic
effects comparable to the one discussed in Section 3.8 for the corresponding systematic effects. After a
journey of
. This would give rise to a magnitude of these nonsystematic
effects comparable to the one discussed in Section 3.8 for the corresponding systematic effects. After a
journey of 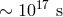 the acquired fuzziness of arrival times could be within the reach [74
the acquired fuzziness of arrival times could be within the reach [74 ] of suitably
arranged gamma-ray-burst studies. However, there is no significant effort to report here on establishing
bounds following this strategy.
] of suitably
arranged gamma-ray-burst studies. However, there is no significant effort to report here on establishing
bounds following this strategy.
There are instead some studies of this phenomenological picture [431 , 72
, 72 , 37
, 37 ], which take as a starting
point the possibility, discussed in Sections 3.4 and 3.5, of modifications of the dispersion relation leading to
modifications of the threshold requirements for certain particle-production processes, such as the case of two
incoming photons producing an outgoing electron-positron pair. Refs. [431, 72
], which take as a starting
point the possibility, discussed in Sections 3.4 and 3.5, of modifications of the dispersion relation leading to
modifications of the threshold requirements for certain particle-production processes, such as the case of two
incoming photons producing an outgoing electron-positron pair. Refs. [431, 72 , 37
, 37 ] considered the
possibility of a non-systematic quantum-spacetime-induced deformation of the dispersion relation,
specifically the case in which the classical relation
] considered the
possibility of a non-systematic quantum-spacetime-induced deformation of the dispersion relation,
specifically the case in which the classical relation 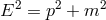 still holds on average, but
for a given particle with large momentum
still holds on average, but
for a given particle with large momentum 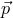 , energy would be somewhere in the range of
, energy would be somewhere in the range of
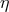 , but each given particle would satisfy a dispersion
relation of the type
with
, but each given particle would satisfy a dispersion
relation of the type
with 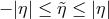 .
.
In analyses such as the one discussed in Section 3.4 (for observations of gamma rays from blazars) one
would then consider electron-positron pair production in a head-on photon-photon collision
assuming that one of the photons is very hard while the other is very soft. To leading order, for the
soft photon only, the energy  is significant (for an already small
is significant (for an already small  the actual value of
the actual value of
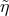 will not matter in leading order). So, the soft photon can, in leading order, be treated
as satisfying a classical dispersion relation. In a quantum-spacetime theory predicting such
non-systematic effects, the hard photon would be characterized both by its energy
will not matter in leading order). So, the soft photon can, in leading order, be treated
as satisfying a classical dispersion relation. In a quantum-spacetime theory predicting such
non-systematic effects, the hard photon would be characterized both by its energy  and its value
of
and its value
of 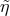 . In order to establish whether a collision between two such photons can produce an
electron-positron pair, one should establish whether, for some admissible values of
. In order to establish whether a collision between two such photons can produce an
electron-positron pair, one should establish whether, for some admissible values of 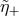 and
and
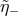 (the values of
(the values of 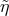 pertaining to the outgoing positron and the electron respectively), the
conditions for energy-momentum conservation can be satisfied. The process will be allowed if
pertaining to the outgoing positron and the electron respectively), the
conditions for energy-momentum conservation can be satisfied. The process will be allowed if
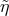 ,
, 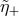 and
and 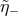 are bound by the range
are bound by the range 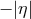 to
to 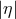 , the process is only allowed, independent
of the value of
, the process is only allowed, independent
of the value of 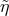 , if the condition
is satisfied. This condition defines the actual threshold in the non-systematic-effect scenario. Clearly, in this
sense the threshold is inevitably decreased by the non-systematic effect. However, there is only a tiny chance
that a given photon would have
, if the condition
is satisfied. This condition defines the actual threshold in the non-systematic-effect scenario. Clearly, in this
sense the threshold is inevitably decreased by the non-systematic effect. However, there is only a tiny chance
that a given photon would have 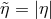 , since this is the limiting case of the range allowed
by the nonsystematic effect, and unless
, since this is the limiting case of the range allowed
by the nonsystematic effect, and unless 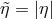 , the process will still not be allowed even if
Moreover, even assuming
, the process will still not be allowed even if
Moreover, even assuming 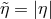 , the energy value described by (57
, the energy value described by (57 ) will only be sufficient to create an
electron positron pair with
) will only be sufficient to create an
electron positron pair with 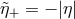 and
and 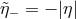 , which again are isolated points at
the extremes of the relevant probability distributions. Therefore the process becomes possible
at the energy level described by (57
, which again are isolated points at
the extremes of the relevant probability distributions. Therefore the process becomes possible
at the energy level described by (57 ) but it remains extremely unlikely, strongly suppressed
by the small probability that the values of
) but it remains extremely unlikely, strongly suppressed
by the small probability that the values of 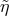 ,
, 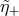 and
and 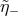 would satisfy the kinematical
requirements.
would satisfy the kinematical
requirements.
With reasoning of this type, one can easily develop an intuition for the dependence on the energy 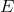 ,
for fixed value of
,
for fixed value of  (and treating
(and treating 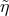 ,
, 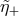 and
and 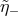 as totally unknown), of the likelihood that the
pair-production process can occur: (i) when (56
as totally unknown), of the likelihood that the
pair-production process can occur: (i) when (56 ) is not satisfied the process is not allowed; (ii) as the value
of
) is not satisfied the process is not allowed; (ii) as the value
of 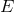 is increased above the value described by (57
is increased above the value described by (57 ), pair production becomes less and less suppressed by
the relevant probability distributions for
), pair production becomes less and less suppressed by
the relevant probability distributions for 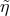 ,
, 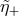 and
and 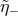 , but some suppression remains up to the value
of
, but some suppression remains up to the value
of 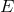 that satisfies
that satisfies
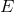 higher than the one described by (58
higher than the one described by (58 ), the process is kinematically allowed for
all values of
), the process is kinematically allowed for
all values of 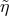 ,
, 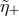 and
and 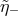 , and, therefore, the likelihood of the process is just the same as in the
classical-spacetime theory.
, and, therefore, the likelihood of the process is just the same as in the
classical-spacetime theory.
This describes a single photon-photon collision taking into account the nonsystematic effects. One
should next consider that for a hard photon traveling toward our Earth detectors from a distant
astrophysical source there are many opportunities to collide with soft photons with energy suitable for
pair production to occur (the mean free path is much shorter than the distance between the
source and the Earth). Thus, one expects [72 , 37
, 37 ] that even a small probability of producing an
electron-positron pair in a single collision would be sufficient to lead to the disappearance of the hard
photon before reaching our detectors. The probability is small in a single collision with a soft
background photon, but the fact that there are, during the long journey, many such pair-production
opportunities renders it likely that in one of the many collisions the hard photon would indeed
disappear into an electron-positron pair. Therefore, for this specific scheme of non-systematic
effects it appears that a characteristic prediction is that the detection of such hard photons from
distant astrophysical sources should start being significantly suppressed already at the energy
level described by (57
] that even a small probability of producing an
electron-positron pair in a single collision would be sufficient to lead to the disappearance of the hard
photon before reaching our detectors. The probability is small in a single collision with a soft
background photon, but the fact that there are, during the long journey, many such pair-production
opportunities renders it likely that in one of the many collisions the hard photon would indeed
disappear into an electron-positron pair. Therefore, for this specific scheme of non-systematic
effects it appears that a characteristic prediction is that the detection of such hard photons from
distant astrophysical sources should start being significantly suppressed already at the energy
level described by (57 ), which is below the threshold corresponding to the classical-spacetime
kinematics.
), which is below the threshold corresponding to the classical-spacetime
kinematics.
It is interesting [57 , 72
, 72 , 74
, 74 ] to contemplate in this case the possibility that systematic and
nonsystematic effects may both be present. It is not unnatural to arrange the framework in such a way that
the systematic effects tend to give higher values of the threshold energy, but then the nonsystematic effects
would allow (with however small probability) configurations below threshold to produce the
electron-positron pair. And for very large propagation distances (very many “target soft photons” available)
the nonsystematic effect can essentially erase [72] the systematic effect (no noticeable upward shift of the
threshold).
] to contemplate in this case the possibility that systematic and
nonsystematic effects may both be present. It is not unnatural to arrange the framework in such a way that
the systematic effects tend to give higher values of the threshold energy, but then the nonsystematic effects
would allow (with however small probability) configurations below threshold to produce the
electron-positron pair. And for very large propagation distances (very many “target soft photons” available)
the nonsystematic effect can essentially erase [72] the systematic effect (no noticeable upward shift of the
threshold).
I illustrated the implications of nonsystematic effects within a given scenario and specifically for the case of observations of gamma rays from blazars. One can implement the non-systematic effects in some alternative ways and the study of the observational implications can consider other contexts. In this respect I should bring to the attention of my readers the studies of non-systematic effects for ultra-high-energy cosmic rays reported in Refs. [37, 310, 106].
Combinations of systematic and nonsystematic effects can also be relevant [57, 74 ] for studies of the
correlations between times of arrival and energy of simultaneously-emitted particles. For that type of study
both the systematic and the nonsystematic effects could leave an observable trace [74] in the data, codified
in the mean arrival time and the standard deviation of arrival times found in different energy
channels.
] for studies of the
correlations between times of arrival and energy of simultaneously-emitted particles. For that type of study
both the systematic and the nonsystematic effects could leave an observable trace [74] in the data, codified
in the mean arrival time and the standard deviation of arrival times found in different energy
channels.
4.3.3 Blurring images of distant sources
The two examples of studies in astrophysics of quantum-spacetime-induced distance fuzziness I discuss in Sections 4.3.1 and 4.3.2 have only been moderately popular. I have left as last the most intensely studied opportunity in astrophysics for quantum-spacetime-induced distance fuzziness. These are studies essentially looking for effects blurring the images of distant sources.
It is interesting that these studies were started by Ref. [367 ], which cleverly combined some aspects of
Refs. [51
], which cleverly combined some aspects of
Refs. [51 , 54
, 54 , 53
, 53 , 433
, 433 ], providing the main concepts for the proposal summarized in Section 4.2,
and some aspects of Ref. [66
], providing the main concepts for the proposal summarized in Section 4.2,
and some aspects of Ref. [66 ], providing the main concepts for the proposal summarized in
Section 3.8. Ref. [367
], providing the main concepts for the proposal summarized in
Section 3.8. Ref. [367 ] was interested in the same phenomenology of distance fuzziness introduced and
analyzed for controlled interferometers in Refs. [51
] was interested in the same phenomenology of distance fuzziness introduced and
analyzed for controlled interferometers in Refs. [51 , 54
, 54 , 53
, 53 , 433
, 433 ], but looked for opportunities to
perform analogous tests using the whole Universe as laboratory, in the sense first introduced in
Ref. [66
], but looked for opportunities to
perform analogous tests using the whole Universe as laboratory, in the sense first introduced in
Ref. [66 ].
].
Gradually over the last decade this became a rather active research area, as illustrated by the studies
reported in Refs. [367 , 434
, 434 , 189
, 189 , 464
, 464 , 363
, 363 , 171
, 171 , 167
, 167 , 402
, 402 , 514
, 514 , 403
, 403 , 404
, 404 , 520
, 520 , 456
, 456 , 405
, 405 ].
].
The phenomenological idea is powerfully simple: effects of quantum-spacetime-induced spacetime
fuzziness had been shown [51 , 54
, 54 , 53
, 53 , 433
, 433 ] to be potentially relevant for LIGO/VIRGO-like (and
LISA-like) intereferometers, exploiting not only the distance-monitoring accuracy of those interferometers,
but also the fact that such accuracy on distance monitoring is achieved for rather large terrestrial distances.
Essentially the Universe gives much larger distances for us to monitor [66], and although we can monitor
them with accuracy inferior to the one of a LIGO/VIRGO-like intereferometer, on balance, the
astrophysics route may also be advantageous also for studies of quantum-spacetime-induced spacetime
fuzziness [367
] to be potentially relevant for LIGO/VIRGO-like (and
LISA-like) intereferometers, exploiting not only the distance-monitoring accuracy of those interferometers,
but also the fact that such accuracy on distance monitoring is achieved for rather large terrestrial distances.
Essentially the Universe gives much larger distances for us to monitor [66], and although we can monitor
them with accuracy inferior to the one of a LIGO/VIRGO-like intereferometer, on balance, the
astrophysics route may also be advantageous also for studies of quantum-spacetime-induced spacetime
fuzziness [367 ].
].
As for Refs. [51, 54, 53, 433], reviewed in Section 4.2, the core intuition here is that the
quantum-spacetime contribution to the fuzziness of a particle’s worldline might grow with propagation
distance. And collecting the scenarios summarized in Eqs. (47 ), (49
), (49 ), and (50
), and (50 ), one arrives at a
one-parameter family of phenomenological ansätze for the characterization of this dependence of fuzziness
on distance
), one arrives at a
one-parameter family of phenomenological ansätze for the characterization of this dependence of fuzziness
on distance
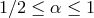 .
.
An assumption shared by most explorations [367 , 434
, 434 , 189, 464, 363, 171
, 189, 464, 363, 171 , 167, 402, 514
, 167, 402, 514 , 403, 404, 520
, 403, 404, 520 , 456, 405]
of this phenomenological avenue is that from Eq. (59
, 456, 405]
of this phenomenological avenue is that from Eq. (59 ), that there would also follow an associated
uncertainty in the specification of momenta
), that there would also follow an associated
uncertainty in the specification of momenta
 ) it is easy to see [367
) it is easy to see [367 ] that it follows that
(assuming a classical-wave description is still admissible when such effects are nonnegligible) there
should be a mismatch between uncertainty in the group velocity and in the phase velocity of
a classical wave, and this in turn proves to be a very powerful tool for the phenomenology.
During a propagation time
] that it follows that
(assuming a classical-wave description is still admissible when such effects are nonnegligible) there
should be a mismatch between uncertainty in the group velocity and in the phase velocity of
a classical wave, and this in turn proves to be a very powerful tool for the phenomenology.
During a propagation time 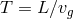 (
(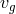 being the group velocity) the phase of a wave
advances by
being the group velocity) the phase of a wave
advances by 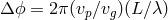 (where
(where 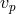 is the phase velocity and
is the phase velocity and 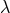 is the wavelength).
There are two schools of intuition concerning how quantitatively spacetime fuzziness should
scramble the phase of a wave. According to Ref. [367] and followers the effect should go as
whereas according to Ref. [434, 171
is the wavelength).
There are two schools of intuition concerning how quantitatively spacetime fuzziness should
scramble the phase of a wave. According to Ref. [367] and followers the effect should go as
whereas according to Ref. [434, 171 ] and followers, the effect should grow more slowly with the distance of
propagation, going like
] and followers, the effect should grow more slowly with the distance of
propagation, going like
As first observed in Ref. [514 ], the alternative formulas (61
], the alternative formulas (61 ) and (62
) and (62 ) should be improved to account for
redshift. For the case of Eq. (62
) should be improved to account for
redshift. For the case of Eq. (62 ) Ref. [514
) Ref. [514 ] proposes the following
] proposes the following
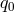 is the decelaration parameter,
is the decelaration parameter, 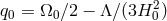 and
and 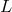 is the luminosity distance,
is the luminosity distance,
![L = [zq + (1 − q )(1 − √1-+-2zq-)]∕(H q2) 0 0 0 0 0](article673x.gif) (
(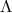 ,
, 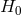 and
and 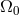 here denote, as usual, respectively the
cosmological constant, the Hubble parameter and the matter fraction).
here denote, as usual, respectively the
cosmological constant, the Hubble parameter and the matter fraction).
Evidently, this phenomenology still has a few too many quantitative details subject to further
scrutiny and a few too many alternative scenarios. This is the result of the fact that work on
actual formalizations of spacetime quantization, while encouraging the general intuitive picture,
has been unable to provide detailed guidance. And the heuristic arguments based on these
preliminary studies have been unable to narrow the range of possibilities. But pursuing this path
further appears to be an exciting opportunity for quantum-spacetime phenomenology, and we
should, therefore, persevere. In particular, based on the (however alternative) estimates given by
Eqs. (61 ), (62
), (62 ), and (63
), and (63 ), several authors (see, e.g., Refs. [171
), several authors (see, e.g., Refs. [171 , 514
, 514 , 520
, 520 ]) have concluded that a
phenomenology based on blurring of the images of distant sources can provide Planck-scale
sensitivity for a rather broad range of possible phenomenological test theories and for values of
]) have concluded that a
phenomenology based on blurring of the images of distant sources can provide Planck-scale
sensitivity for a rather broad range of possible phenomenological test theories and for values of 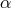 significantly greater than
significantly greater than 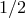 , possibly [520
, possibly [520 ] going all the way up to values of
] going all the way up to values of 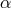 close to 1. In
Ref. [514
close to 1. In
Ref. [514 ] one even finds a preliminary data analysis suggesting that for observations of quasars
there might be a trend towards lower observed Strehl ratios with increasing redshift, which
would provide encouragement for the hope of discovering quantum-spacetime-induced image
blurring.
] one even finds a preliminary data analysis suggesting that for observations of quasars
there might be a trend towards lower observed Strehl ratios with increasing redshift, which
would provide encouragement for the hope of discovering quantum-spacetime-induced image
blurring.
The main opportunities appear to be provided by observations of distant quasars [171, 514, 520], whose dimensions are small and are rather abundantly observed at high redshift.
4.4 Planck-scale modifications of CPT symmetry and neutral-meson studies
Investigations of spacetime symmetries and distance fuzziness are evidently relevant for some of the core features of the idea of spacetime quantization. My next task concerns CPT-symmetry tests, and the possibility that indirectly some scenarios for the quantization of spacetime might affect CPT symmetry.
A complication, but also an opportunity, for quantum-spacetime-motivated tests of CPT symmetries comes from the fact that CPT symmetry should be and is tested independently of the quantum-spacetime motivation. From this perspective the situation is somewhat analogous to that discussed earlier concerning quantum-spacetime-motivated tests of Lorentz symmetry. The quantum spacetime literature can provide special motivation for probing CPT symmetry in certain specific ways, but there is already plenty of motivation, even without quantum-spacetime research, for testing CPT symmetry as broadly as possible [389, 439, 234].
Also, in this case, the Standard Model Extension provides a much appreciated and widely adopted formalization, finding a good balance between the desire of searching for violations of CPT symmetry (and/or, as mentioned, violations of Lorentz symmetry) within the confines of quantum field theory but allowing for both effects that have been discussed from the quantum-spacetime perspective and effects for which so far there is no quantum-spacetime motivation. I shall focus here on the hypothesis of quantum-spacetime-induced and Planck-scale-magnitude CPT violation effects, so I shall not review the broad subject of CPT violation within the Standard Model Extension, for which readers can find valuable reviews and perspectives in Refs. [345, 117, 180, 339, 299, 341, 346] (see also parts of Ref. [395]).
Another issue that should always be kept in mind in relation to CPT symmetry is the fact that it can be derived as a theorem for local quantum field theories with Lorentz invariance. In approaches based on local field theory, it is natural to perform combined studies of CPT and Lorentz symmetry.31 However, the notion of spacetime quantization at the Planck scale involves some aspects of nonlocality (at least the notion of points that coincide with accuracy better than the Planck length is typically abandoned) and in most quantum-spacetime studies of the fate of CPT symmetry the expectation is that these aspects of non-locality may be primarily responsible for the conjectured violations of CPT symmetry.
I shall not attempt to summarize here the results on violations of CPT symmetry arising from spacetime quantization not introduced at the Planck scale (but rather at some much lower scale), for which readers can find valuable starting points to the related literature in Refs. [162, 43, 417, 496, 28] and references therein.
Consistent with the scope of this review, I shall focus exclusively on scenarios for violations of CPT symmetry based on nonclassicality (“quantization”) of spacetime introduced at the Planck scale. As a result of some technical challenges, mentioned in Section 2.2.2, this literature can only rely on preliminary theory results, but does suggest convincingly that Planck-scale sensitivity to quantum-spacetime-induced violations of CPT symmetry is within our reach.
4.4.1 Broken-CPT effects from Liouville strings
In the case of the test of CPT symmetry it is easier for me to start by discussing the availability of Planck-scale sensitivity, postponing briefly some comments on test theories based on the idea of spacetime quantization.
There is a sizable literature establishing that CPT symmetry can be tested with Planck-scale sensitivity
in the neutral-kaon and the neutral-B systems (see, e.g., Refs. [219 , 220
, 220 , 298
, 298 , 108
, 108 ]). It turns out that in
these neutral-meson systems there are plenty of opportunities for Planck-scale departures from
CPT symmetry to be amplified. In particular, the neutral-kaon system hosts the peculiarly
small mass difference between long-lived and short-lived kaons
]). It turns out that in
these neutral-meson systems there are plenty of opportunities for Planck-scale departures from
CPT symmetry to be amplified. In particular, the neutral-kaon system hosts the peculiarly
small mass difference between long-lived and short-lived kaons 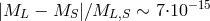 and other small numbers naturally show up in the analysis of the system, such as the ratio
and other small numbers naturally show up in the analysis of the system, such as the ratio
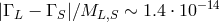 . And for certain types of departures from CPT symmetry the inverse of
one of these small numbers amplifies the small CPT-violation effect [219, 220
. And for certain types of departures from CPT symmetry the inverse of
one of these small numbers amplifies the small CPT-violation effect [219, 220 , 298, 108
, 298, 108 ]. In
particular, this mechanism turns out to provide sufficient amplification for Planck-scale effects,
inducing a difference of order
]. In
particular, this mechanism turns out to provide sufficient amplification for Planck-scale effects,
inducing a difference of order 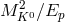 between the terms on the diagonal of the
between the terms on the diagonal of the 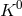 ,
, 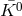 mass matrix (exact classical CPT symmetry would require the terms on the diagonal to be
identical). It should be noticed that
mass matrix (exact classical CPT symmetry would require the terms on the diagonal to be
identical). It should be noticed that 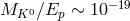 , which is not overwhelmingly smaller than
, which is not overwhelmingly smaller than
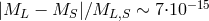 .
.
A much studied quantum-spacetime description of violations of CPT symmetry is centered on the
mentioned Liouville-strings approach [221 , 220
, 220 ], particularly with its description of spacetime foam and its
non-classical description of time, involving a non-trivial role for the Liouville field [224]. This model is, in
particular, the reference for the analysis of Planck-scale limits on quantum-spacetime-induced CPT
violation reported by the CPLEAR collaboration on the basis of studies of neutral kaons [13
], particularly with its description of spacetime foam and its
non-classical description of time, involving a non-trivial role for the Liouville field [224]. This model is, in
particular, the reference for the analysis of Planck-scale limits on quantum-spacetime-induced CPT
violation reported by the CPLEAR collaboration on the basis of studies of neutral kaons [13 ] (also see the
related results reported using neutral-kaon data gathered at the particle-physics laboratory in
Frascati [13
] (also see the
related results reported using neutral-kaon data gathered at the particle-physics laboratory in
Frascati [13 , 534
, 534 , 205
, 205 ]). Interestingly, the Liouville-string model hosts both departures from CPT
symmetry and decoherence, and I find it most convenient to discuss it in the later part of this section
devoted to decoherence studies.
]). Interestingly, the Liouville-string model hosts both departures from CPT
symmetry and decoherence, and I find it most convenient to discuss it in the later part of this section
devoted to decoherence studies.
Let me highlight a recent development that is in part inspired by these Liouville-string studies. It was
recently observed (primarily in Refs. [112 , 113
, 113 ]) that quantum-spacetime scenarios with violations of CPT
symmetry might also require some corresponding modifications of the recipe for obtaining multiparticle
states from single-particle states for identical particles. This may apply in particular to the
neutral-kaon
]) that quantum-spacetime scenarios with violations of CPT
symmetry might also require some corresponding modifications of the recipe for obtaining multiparticle
states from single-particle states for identical particles. This may apply in particular to the
neutral-kaon 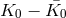 system, since standard CPT transformations take
system, since standard CPT transformations take 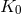 into
into 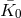 but
violations of CPT symmetry are likely to also induce a modification of the link between
but
violations of CPT symmetry are likely to also induce a modification of the link between 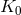 and
and
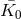 .
.
Refs. [112 , 113
, 113 ] proposed a phenomenology inspired by this argument and based on the following
parametrization of the state
] proposed a phenomenology inspired by this argument and based on the following
parametrization of the state 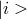 initially produced by a
initially produced by a 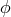 -meson decay:
-meson decay:
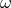 essentially characterizes the level of contamination of the state
essentially characterizes the level of contamination of the state 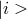 by
the (otherwise unexpected) C-even component
by
the (otherwise unexpected) C-even component  .
.
Stringent constraints on  can be placed by performing measurements of the chain of processes
can be placed by performing measurements of the chain of processes
 , in which first the
, in which first the 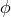 meson decays into a pair of neutral kaons and then one
of the kaons decays at time
meson decays into a pair of neutral kaons and then one
of the kaons decays at time 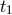 into a final state
into a final state 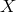 , while the other kaon decays at time
, while the other kaon decays at time
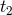 into a final state
into a final state 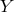 . By following this strategy the KLOE experiment [534
. By following this strategy the KLOE experiment [534 , 522] at
DA
, 522] at
DA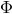 NE is setting [204, 205
NE is setting [204, 205 ] experimental limits on
] experimental limits on 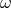 at the level
at the level  (
( ,
,
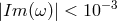 ).
).
It is not easy at present to establish robustly what level of sensitivity to 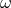 could really amount to
Planck-scale sensitivity, but it is noteworthy that there are semi-quantitative/semi-heuristic estimates based
on a certain intuition for spacetime foam suggesting [112, 113, 398
could really amount to
Planck-scale sensitivity, but it is noteworthy that there are semi-quantitative/semi-heuristic estimates based
on a certain intuition for spacetime foam suggesting [112, 113, 398 ] that sensitivities in the neighborhood
of
] that sensitivities in the neighborhood
of 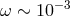 ,
, 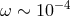 could already be significant.
could already be significant.
4.4.2 Departures from classical CPT symmetry from spacetime noncommutativity at the Planck scale
Another formalism for spacetime quantization at the Planck scale where violations of CPT symmetry have
been discussed to some extent is “ -Minkowski spacetime noncommutativity” [391, 374, 70
-Minkowski spacetime noncommutativity” [391, 374, 70 ]. A first hint
that this might be appropriate comes from the fact that the
]. A first hint
that this might be appropriate comes from the fact that the  -Minkowski formalism is one of those
providing support for the possibility of modifications of the dispersion relation of the form
-Minkowski formalism is one of those
providing support for the possibility of modifications of the dispersion relation of the form
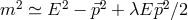 , with
, with  on the order of the Planck length. It may be relevant for the relation
between particles and antiparticles (for which CPT symmetry is a crucial player) that for the values of
on the order of the Planck length. It may be relevant for the relation
between particles and antiparticles (for which CPT symmetry is a crucial player) that for the values of  allowed by the dispersion relation for given
allowed by the dispersion relation for given  one does not recover the ordinary result (with its
traditional two solutions of equal magnitude and opposite sign); instead, one finds that the two solutions
one does not recover the ordinary result (with its
traditional two solutions of equal magnitude and opposite sign); instead, one finds that the two solutions
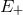 ,
, 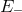 are given by
are given by
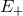 and
and 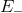 are not exactly opposite may suggest that one should make
room for a mismatch
are not exactly opposite may suggest that one should make
room for a mismatch 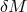 of the terms on the diagonal of the
of the terms on the diagonal of the 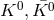 mass matrix, of order
The most significant feature of this description of
mass matrix, of order
The most significant feature of this description of 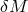 is its momentum dependence, and, for
given
is its momentum dependence, and, for
given 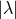 ,
, 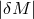 is an increasing function of
is an increasing function of 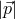 , quadratic in the non-relativistic limit and
linear in the ultra-relativistic limit. Therefore, among experiments achieving comparable
, quadratic in the non-relativistic limit and
linear in the ultra-relativistic limit. Therefore, among experiments achieving comparable 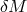 sensitivity the ones studying more energetic kaons are going to lead to more stringent bounds on
sensitivity the ones studying more energetic kaons are going to lead to more stringent bounds on
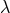 .
.
Considering that, as mentioned, neutral-kaon experiments at 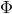 factories are now sensitive at the
level
factories are now sensitive at the
level 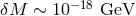 , one infers a sensitivity to this type of candidate quantum-gravity
effect that, for kaons of momenta of about 110 MeV (at the
, one infers a sensitivity to this type of candidate quantum-gravity
effect that, for kaons of momenta of about 110 MeV (at the 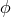 resonance), corresponds to a
sensitivity to values of
resonance), corresponds to a
sensitivity to values of 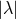 around
around 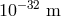 , i.e., not far (just 3 orders of magnitude away)
from the Planck scale. Because of the premium on high momenta of this scenario, better limits
could be set using experiments with high-momentum kaons Fermilab’s E731 [554, 450]. And
studies with neutral B mesons of relatively high momenta could also be valuable from this
perspective.
, i.e., not far (just 3 orders of magnitude away)
from the Planck scale. Because of the premium on high momenta of this scenario, better limits
could be set using experiments with high-momentum kaons Fermilab’s E731 [554, 450]. And
studies with neutral B mesons of relatively high momenta could also be valuable from this
perspective.
However, we are at a very early stage of understanding of the fate of CPT symmetry in these spacetimes
with quantization at the Planck scale. Specifically, for the case of  -Minkowski spacetime, analyses such
as the one in Ref. [70] suggest that CPT symmetry is deformed rather than broken/lost. Indeed, in
-Minkowski spacetime, analyses such
as the one in Ref. [70] suggest that CPT symmetry is deformed rather than broken/lost. Indeed, in
 -Minkowski the anomalies one can presently preliminarily see for CPT symmetry are all linked to the
peculiarity of
-Minkowski the anomalies one can presently preliminarily see for CPT symmetry are all linked to the
peculiarity of 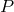 -parity transformations. It appears that in
-parity transformations. It appears that in  -Minkowski
-Minkowski 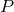 -parity transformations for
momenta should not take a momentum
-parity transformations for
momenta should not take a momentum 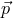 into
into 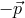 , but rather
, but rather 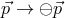 , where
, where  denotes the
“antipode operation”:
denotes the
“antipode operation”: 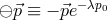 (where
(where 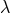 denotes again the
denotes again the  -Minkowski noncommutativity
length scale).
-Minkowski noncommutativity
length scale).
4.5 Decoherence studies with kaons and atoms
4.5.1 Spacetime foam as decoherence effects and the “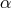 ,
, 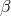 ,
, 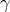 test theory”
test theory”
As stressed earlier in this review the idea of “spacetime foam” appears to appeal to everyone involved
in quantum-spacetime research, but this is in part due to the fact that this idea is not really
well defined, not by the qualitative intuitive picture proposed by Wheeler. In order to set up a
phenomenology for effects induced by this spacetime foam, it is necessary to provide for it
physical/experimentally-meaningful characterizations. I already discussed one possible such
characterization, given in terms of distance fuzziness and associated strain noise for interferometry.
Another attempt to physically characterize spacetime foam can be found in Refs. [220 , 221
, 221 ]
(other valuable perspectives on this subject can be found in Refs. [108, 251]), focusing on the
possibility that the rich dynamical properties of spacetime foam might act as a decoherence-inducing
environment.
]
(other valuable perspectives on this subject can be found in Refs. [108, 251]), focusing on the
possibility that the rich dynamical properties of spacetime foam might act as a decoherence-inducing
environment.
The main focus of Refs. [220 , 221
, 221 ] has been the neutral-kaon system, whose remarkably delicate balance
of scales provides opportunities not only for very sensitive tests of CPT symmetry, but also for very
sensitive tests of decoherence. Refs. [220, 221] essentially propose a test theory, based on the mentioned
Liouville-strings idea, for spacetime-foam-induced decoherence in the neutral-kaon system. This test theory
adopts the formalism of density matrices and is centered on the following evolution equation for the
neutral-kaon reduced density matrix
] has been the neutral-kaon system, whose remarkably delicate balance
of scales provides opportunities not only for very sensitive tests of CPT symmetry, but also for very
sensitive tests of decoherence. Refs. [220, 221] essentially propose a test theory, based on the mentioned
Liouville-strings idea, for spacetime-foam-induced decoherence in the neutral-kaon system. This test theory
adopts the formalism of density matrices and is centered on the following evolution equation for the
neutral-kaon reduced density matrix 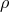 :
:
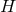 is an ordinary-quantum-mechanics Hamiltonian and
is an ordinary-quantum-mechanics Hamiltonian and 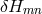 (with indices
(with indices 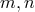 running from
1 to 4:
running from
1 to 4: 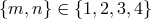 ) is the spacetime-foam-induced decoherence matrix, taken to be such that
) is the spacetime-foam-induced decoherence matrix, taken to be such that
 , while
, while  ,
,  , and
, and 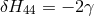 .
Therefore, the test theory is fully specified upon fixing
.
Therefore, the test theory is fully specified upon fixing  and giving some definite values to the
parameters
and giving some definite values to the
parameters  ,
,  ,
, 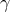 .
.
It should be stressed that this test theory necessarily violates CPT symmetry whenever
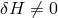 . Additional CPT violating features may be introduced in the ordinary-quantum-mechanics
Hamiltonian
. Additional CPT violating features may be introduced in the ordinary-quantum-mechanics
Hamiltonian  , by allowing for differences in masses and/or differences in widths between
particles and antiparticles. Therefore, this test theory is an example of a framework that could be
used in a phenomenology looking simultaneously for departures from CPT symmetry of types
admissible within ordinary quantum mechanics and for departures from CPT symmetry that
require going beyond quantum mechanics (by allowing for decoherence). It is noteworthy that
the two types of CPT violation (within and beyond quantum mechanics) can be distinguished
experimentally.
, by allowing for differences in masses and/or differences in widths between
particles and antiparticles. Therefore, this test theory is an example of a framework that could be
used in a phenomenology looking simultaneously for departures from CPT symmetry of types
admissible within ordinary quantum mechanics and for departures from CPT symmetry that
require going beyond quantum mechanics (by allowing for decoherence). It is noteworthy that
the two types of CPT violation (within and beyond quantum mechanics) can be distinguished
experimentally.
Concerning more directly decoherence, various characterizations of the effects of this test theory have
been provided, and in particular a valuable description of how significant the decoherence effects are
(depending on the values given to 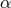 ,
, 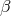 ,
, 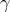 ) is found looking at how the rate of kaon decay into a pair
of pions,
) is found looking at how the rate of kaon decay into a pair
of pions,  , evolves as a function of time. This time evolution will in general take the form
, evolves as a function of time. This time evolution will in general take the form
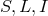 stand respectively for short-lived, long-lived, interference, and the combination
stand respectively for short-lived, long-lived, interference, and the combination
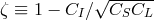 provides a good phenomenological characterization of the amount of decoherence
induced in the system [398
provides a good phenomenological characterization of the amount of decoherence
induced in the system [398 ].
].
Using data gathered by the CPLEAR experiment [13], one can set bounds on  at the levels
at the levels
 ,
,  , and
, and 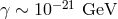 . A comparable limit on
. A comparable limit on  has been placed by
DA
has been placed by
DA NE’s KLOE experiment, and in that case the analysis was based [398, 534, 205] on entangled kaon
states.
NE’s KLOE experiment, and in that case the analysis was based [398, 534, 205] on entangled kaon
states.
I should stress that this is clearly a quantum-spacetime picture (at least in as much as it models
spacetime foam) and the objective of the associated research program is to introduce quantum/foamy
properties of spacetime at the Planck scale, but it is at present still unclear which levels of sensitivity to
 ,
, 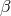 ,
, 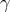 would correspond to foaminess of spacetime at the Planck scale. We are still unable to
perform a derivation starting from foaminess at the Planck scale and deriving corresponding values for
would correspond to foaminess of spacetime at the Planck scale. We are still unable to
perform a derivation starting from foaminess at the Planck scale and deriving corresponding values for 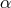 ,
,
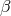 ,
, 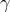 . It is nonetheless encouraging that the present experimental limits on these (dimensionful)
parameters are in a neighborhood of the Planck-scale-inspired quantification
. It is nonetheless encouraging that the present experimental limits on these (dimensionful)
parameters are in a neighborhood of the Planck-scale-inspired quantification 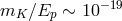 (but it
should be noticed that as much “Planck-scale inspiration” should be attributed, for example, to the scale
(but it
should be noticed that as much “Planck-scale inspiration” should be attributed, for example, to the scale
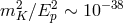 ).
).
4.5.2 Other descriptions of foam-induced decoherence for matter interferometry
Another attempt to characterize spacetime foam as a decoherence-inducing medium was developed by
Percival and collaborators (see, e.g., Refs. [452 , 453
, 453 , 454
, 454 ]). This approach assumes that ordinary quantum
systems should all be treated as open systems due to neglecting the degrees of freedom of the spacetime
foam, but, rather than a formalization using density matrices, Refs. [452, 453, 454
]). This approach assumes that ordinary quantum
systems should all be treated as open systems due to neglecting the degrees of freedom of the spacetime
foam, but, rather than a formalization using density matrices, Refs. [452, 453, 454 ] adopt a formalism in
which an open quantum system is represented by a pure state diffusing in Hilbert space. The dynamics
of such states is formulated in terms of “Primary state diffusion”, an alternative to quantum
theory with only one free parameter, a time scale
] adopt a formalism in
which an open quantum system is represented by a pure state diffusing in Hilbert space. The dynamics
of such states is formulated in terms of “Primary state diffusion”, an alternative to quantum
theory with only one free parameter, a time scale 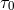 , which one can set to be the Planck time
, which one can set to be the Planck time
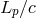 .
.
One way to charaterize  is through a formula for the proper time interval for a timelike segment,
which is given by [454
is through a formula for the proper time interval for a timelike segment,
which is given by [454 ]
]
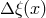 are point-dependent fluctuations induced by the foaminess/quantization of spacetime, which
are modelled within the proposed theory.
are point-dependent fluctuations induced by the foaminess/quantization of spacetime, which
are modelled within the proposed theory.
A key characteristic of this picture would be [454 ] a suppression of the interference pattern for
interferometers using beams of massive particles (such that the original beam is first split and then reunited
to seek an interference pattern). The suppression increases with the mass of the particles, so it could more
easily be tested with atom interferometers (rather than neutron interferometers). Unfortunately, a realistic
analysis of an interferometer in the relevant primary-state-diffusion formalism is much beyond the level of
answers one is (at least presently) able to extract from the primary-state-diffusion setup. Ref. [454
] a suppression of the interference pattern for
interferometers using beams of massive particles (such that the original beam is first split and then reunited
to seek an interference pattern). The suppression increases with the mass of the particles, so it could more
easily be tested with atom interferometers (rather than neutron interferometers). Unfortunately, a realistic
analysis of an interferometer in the relevant primary-state-diffusion formalism is much beyond the level of
answers one is (at least presently) able to extract from the primary-state-diffusion setup. Ref. [454 ]
considered resorting to some simple-minded simplifications, including the assumption that the Hamiltonian
be given by the mass together with projectors onto the wave packets in the arms of the interferometer,
neglecting the kinetic-energy terms. Within such simplifications one does find that values of
]
considered resorting to some simple-minded simplifications, including the assumption that the Hamiltonian
be given by the mass together with projectors onto the wave packets in the arms of the interferometer,
neglecting the kinetic-energy terms. Within such simplifications one does find that values of  at or even
a few orders of magnitude below the Planck time would leave an observably large trace in modern atom
interferometers. However, these simplifications amount to a model of the interferometer that is much
too crude (as acknowledged by the authors themselves [454]) and this does not allow us to
meaningfully explore the possibility of genuine Planck-scale sensitivities being achieved by this
strategy. Note that by taking
at or even
a few orders of magnitude below the Planck time would leave an observably large trace in modern atom
interferometers. However, these simplifications amount to a model of the interferometer that is much
too crude (as acknowledged by the authors themselves [454]) and this does not allow us to
meaningfully explore the possibility of genuine Planck-scale sensitivities being achieved by this
strategy. Note that by taking 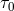 as the Planck time it is not obvious that the effects are being
introduced genuinely at the Planck scale, since the nature of the effects is characterized not only by
as the Planck time it is not obvious that the effects are being
introduced genuinely at the Planck scale, since the nature of the effects is characterized not only by
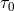 but also by other aspects of the framework, such as the description of the fluctuations.
Moreover, even if all other aspects of the picture were understood, the crudity of the model used
for matter interferometers would still not allow us to investigate the Planck-scale-sensitivity
issue.
but also by other aspects of the framework, such as the description of the fluctuations.
Moreover, even if all other aspects of the picture were understood, the crudity of the model used
for matter interferometers would still not allow us to investigate the Planck-scale-sensitivity
issue.
Recently, Ref. [498] and Ref. [541 ] presented somewhat different pictures of quantum-gravity-induced
decoherence for atom interferometers. Several aspects of the Percival setup are maintained but different
interpretations are applied in some aspects of the analysis. For example, Ref. [541
] presented somewhat different pictures of quantum-gravity-induced
decoherence for atom interferometers. Several aspects of the Percival setup are maintained but different
interpretations are applied in some aspects of the analysis. For example, Ref. [541 ] removes some of the
assumptions adopted by Percival and collaborators, particularly in relation to the description of the “quantum
fluctuations” of the metric, and proposes an estimate of the amount of suppression of the interference
pattern,32
that is perhaps more intriguing from a phenomenology perspective, since it would suggest that the
effect is just beyond present sensitivities (but within the reach of sensitivities achievable by
atom interferometers in the not-so-distant future). For these recent proposals one is still (for
reasons analogous to these just discussed for the Percival approach) unable to meaningfully
explore the issue of “genuine Planck-scale sensitivity”, but they may represent a step in the
direction of a more detailed description of spacetime foam, if intended as fluctuations of the
metric.
] removes some of the
assumptions adopted by Percival and collaborators, particularly in relation to the description of the “quantum
fluctuations” of the metric, and proposes an estimate of the amount of suppression of the interference
pattern,32
that is perhaps more intriguing from a phenomenology perspective, since it would suggest that the
effect is just beyond present sensitivities (but within the reach of sensitivities achievable by
atom interferometers in the not-so-distant future). For these recent proposals one is still (for
reasons analogous to these just discussed for the Percival approach) unable to meaningfully
explore the issue of “genuine Planck-scale sensitivity”, but they may represent a step in the
direction of a more detailed description of spacetime foam, if intended as fluctuations of the
metric.
4.6 Decoherence and neutrino oscillations
The observations briefly discussed in the previous Section 4.5 that are relevant for the study of
manifestations of foam-induced decoherence in some laboratory experiments (neutral-meson studies, atom
interferometers) can very naturally be applied to neutrino astrophysics as well, as discussed in Ref. [400 ]
and references therein (see also Refs. [109, 23, 422, 241]). Also in the neutrino context it is natural to
attempt to develop test theories codifying the intuition that spacetime foam may act as an environment, so
that neutrino observations would have to be analyzed considering the relevant neutrino system as an open
system. And the evolution of the neutrino density matrix could be described (in the same sense as
the description in Eq. (67
]
and references therein (see also Refs. [109, 23, 422, 241]). Also in the neutrino context it is natural to
attempt to develop test theories codifying the intuition that spacetime foam may act as an environment, so
that neutrino observations would have to be analyzed considering the relevant neutrino system as an open
system. And the evolution of the neutrino density matrix could be described (in the same sense as
the description in Eq. (67 ) for neutral-meson systems) by an evolution equation of the type
) for neutral-meson systems) by an evolution equation of the type
 ] that such a formalization of the effects of spacetime foam should generate a
contribution to the mass difference between different netrinos, and could give rise to neutrino oscillations
constituting a “gravitational MSW effect”.
] that such a formalization of the effects of spacetime foam should generate a
contribution to the mass difference between different netrinos, and could give rise to neutrino oscillations
constituting a “gravitational MSW effect”.
As an alternative to the setup of Eq. (70 ) one could consider [400
) one could consider [400 , 401
, 401 ] the possibility of random
(Gaussian) fluctuations of the background spacetime metric over which the neutrinos propagates. For the
random metric one can take [400
] the possibility of random
(Gaussian) fluctuations of the background spacetime metric over which the neutrinos propagates. For the
random metric one can take [400 , 401
, 401 ] a formalization of the type
] a formalization of the type
 , 401
, 401 ] for the random Gaussian variables
] for the random Gaussian variables 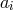 a parametrization based on parameters
a parametrization based on parameters 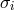 (one per
(one per 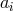 ) such that
) such that 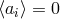 and
and 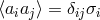 . These fluctuations of the metric are
found [400
. These fluctuations of the metric are
found [400 , 401
, 401 ] to induce decoherence even when the neutrinos are assumed to evolve according to a
standard Hamiltonian setup,
But the decoherence effects generated in this framework with standard Hamiltonian evolution in a
nonstandard (randomly-fluctuating) metric, are significantly different from the ones generated with the
nonstandard evolution equation (70
] to induce decoherence even when the neutrinos are assumed to evolve according to a
standard Hamiltonian setup,
But the decoherence effects generated in this framework with standard Hamiltonian evolution in a
nonstandard (randomly-fluctuating) metric, are significantly different from the ones generated with the
nonstandard evolution equation (70 ) in a standard classical metric. In particular, in both cases one obtains
neutrino-transition probabilities with decoherence-induced exponential damping factors in front of the
oscillatory terms, but in the framework with evolution equation (70
) in a standard classical metric. In particular, in both cases one obtains
neutrino-transition probabilities with decoherence-induced exponential damping factors in front of the
oscillatory terms, but in the framework with evolution equation (70 ) the scaling with the oscillation length
(time) is naturally linear [400
) the scaling with the oscillation length
(time) is naturally linear [400 , 401
, 401 ], whereas when adopting standard Hamiltonian evolution in a
fluctuating metric it is natural [400
], whereas when adopting standard Hamiltonian evolution in a
fluctuating metric it is natural [400 , 401] to have quadratic scaling with the oscillation length
(time).
, 401] to have quadratic scaling with the oscillation length
(time).
The growing evidence for ordinary-physics neutrino oscillations, which one expects to be much more significant than the foam-induced ones, provides a formidable challenge for the phenomenology based on these test theories for foam-induced decoherence in the neutrino sector. Some preliminary ideas on how to overcome this difficulty are described in Ref. [400]. From the strict quantum-spacetime-phenomenology perspective of requiring one to establish that the relevant measurements could be sensitive to effects introduced genuinely at the Planck scale, these neutrino-decoherence test theories must face challenges already discussed for a few other test theories: there is at present no rigorous/constructive derivation of the values of the parameters of these test theories from a description (be it a full quantum-spacetime theory or simply a toy model) of effects introduced genuinely at the Planck scale, so one can only express these parameters in terms of the Planck scale using some dimensional-analysis arguments.
4.7 Planck-scale violations of the Pauli Exclusion Principle
A case for Planck-scale sensitivity was recently made [97 , 99
, 99 ] for the hypothesis of possible violations
of the Pauli Exclusion Principle. This has still not been metabolized by an appreciably-wide
quantum-gravity community, but it certainly deserves to be highlighted briefly in this review, since the
chances for gradually gaining a strong impact on quantum-spacetime phenomenology are rather
high.
] for the hypothesis of possible violations
of the Pauli Exclusion Principle. This has still not been metabolized by an appreciably-wide
quantum-gravity community, but it certainly deserves to be highlighted briefly in this review, since the
chances for gradually gaining a strong impact on quantum-spacetime phenomenology are rather
high.
As observed already a few times in this review, the spin-statistics theorem assumes a classical spacetime with ordinary locality. Therefore, it is legitimate to speculate that small departures from the implications of the spin-statistics theorem may arise in a quantum spacetime. Some earlier suggestions that this might be the case can be found, e.g., in Refs. [98, 163, 86], but the setup then was not such that one could see an emerging case for Planck-scale sensitivity.
The recent studies reported in Refs. [97 , 99
, 99 ] investigated this issues assuming the specific form of
spacetime noncommutativity given by
] investigated this issues assuming the specific form of
spacetime noncommutativity given by
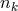 are the components of a fixed spatial unit vector and the deformation length scale
are the components of a fixed spatial unit vector and the deformation length scale 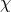 can be
taken to be on the order of the Planck length.
can be
taken to be on the order of the Planck length.
It is rather easy to show that this form of noncommutativity imposes a corresponding modification of
the “flip operator”, i.e., the operator that is used for symmetrization (anti-symmetrization) purposes in the
commutative-spacetime case. In turn this gives rise to a deformed description of bosons and
fermions. And the end result is that certain transitions that would be Pauli-forbidden in a
commutative spacetime are actually allowed, although at a small rate (suppressed by the smallness of
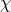 ).
).
Computing these rates on the basis of Eq. (73 ) is at present only possible by relying on an
uncomfortable number of simplifying assumptions [97, 99], but the outcome is nonetheless intriguing since
it suggests that sensitivity to values of
) is at present only possible by relying on an
uncomfortable number of simplifying assumptions [97, 99], but the outcome is nonetheless intriguing since
it suggests that sensitivity to values of 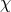 on the order of the Planck length is within reach. This exploits
the high sensitivity toward possible violations of the Pauli Exclusion Principle at ongoing experiments, such
as Borexino [107] and VIP [105].
on the order of the Planck length is within reach. This exploits
the high sensitivity toward possible violations of the Pauli Exclusion Principle at ongoing experiments, such
as Borexino [107] and VIP [105].
4.8 Phenomenology inspired by causal sets
Most of the quantum-spacetime phenomenology of this past decade has been inspired by results on
spacetime noncommutativity and/or LQG. But several other approaches are getting closer to inspiring
phenomenological programs. I share the view of many quantum-spacetime phenomenologists who are
looking at the approach based on causal dynamical triangulations [45, 371, 46, 47, 372, 49]
as a maturing opportunity for inspiring the phenomenology work. And first indications are
coming from the “asymptotic safety approach” [544, 466, 212, 469 , 468], on which I shall
comment in relation to a tangible proposal for phenomenology later in this review. Certainly
in recent years we have seen a blossoming phenomenology emerging from the the causal-set
program.
, 468], on which I shall
comment in relation to a tangible proposal for phenomenology later in this review. Certainly
in recent years we have seen a blossoming phenomenology emerging from the the causal-set
program.
I place here an aside on this recent phenomenology inspired by the causal-set program, which also allows me to return, from a different perspective, on the important subject of non-systematic effects, already briefly discussed in Section 4.3.2. Indeed, because of the perspective that guides that research program, most (if not all) new effects predicted within the causal set program will be of non-systematic type.
Causal sets are a discretization of spacetime that allows the symmetries of GR to be preserved in the continuum approximation [131, 470, 284]. And causal sets can be used to construct simple models suitable for exploring possible manifestations of fuzziness of quantum spacetime. Moreover, the causal set proposal has recently been combined with the loop representation to formulate “causal spin foams” [392], thereby establishing a link to an already mature source of inspiration for quantum-spacetime phenomenology.
Clearly, some of the manifestations one must expect from a causal-set setup fall within the class of phenomena already briefly described in Section 4.3.1: at a coarse-grained level of analysis a causal-set background should introduce an intrinsic limitation to the accuracy of lengths and durations. Several recent works were aimed at formalizing and modeling these aspects of fuzziness for propagation [311, 312, 215]. The preliminary indications that are emerging appear to suggest that, if discreteness is indeed introduced at the Planck scale, the effects are very soft (hard to detect). Nonetheless we do already have a few examples of studies aiming for tangible predictions to be compared to actual data: for example, Ref. [490] reports a causal-set-inspired analysis of possible fuzziness of arrival times (the sort of effects already discussed in Section 4.3.1), relevant for studies conducted by gamma-ray telescopes.
An intriguing effect of random fluctuations in photon polarization can also be motivated by the causal-set framework [186]. The presently-available models of this causal-set-induced effect are to be viewed as very crude/preliminary, particularly since the present understanding of the framework is still not at the point of providing a definite model of photons propagating on a causal set background (from which one could derive the polarization-fluctuation feature). Still, this appears a very promising direction, especially since experimental information on CMB polarization is improving quickly and will keep improving in the coming years.
Presently the most tangible phenomenological plans inspired by the causal-set framework revolve around
an effect [214 , 458] of Lorentz invariant diffusion in the 4-momentum of massive particles. This is an
Ornstein–Uhlenbeck process, a diffusion process on the mass-shell that results in a stochastic
evolution in spacetime. An intuitive picture for this mechanism was given in Ref. [214
, 458] of Lorentz invariant diffusion in the 4-momentum of massive particles. This is an
Ornstein–Uhlenbeck process, a diffusion process on the mass-shell that results in a stochastic
evolution in spacetime. An intuitive picture for this mechanism was given in Ref. [214 ], by
considering a classical particle, of mass
], by
considering a classical particle, of mass 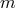 propagating on a random spacetime lattice. The particle
would then be constrained to move from point to point, but the discretization is such that in
order to “reach the next point” (remaining on the lattice) the particle must ‘swerve’ slightly,
also adapting its velocity
propagating on a random spacetime lattice. The particle
would then be constrained to move from point to point, but the discretization is such that in
order to “reach the next point” (remaining on the lattice) the particle must ‘swerve’ slightly,
also adapting its velocity  to the swerving (also see Ref. [457] for a comparison of possible
variants of the description of particle propagation in causal-set theory). The change in velocity
amounts to the particle jumping to a different point on its mass shell. The net result of this
swerving is that [214
to the swerving (also see Ref. [457] for a comparison of possible
variants of the description of particle propagation in causal-set theory). The change in velocity
amounts to the particle jumping to a different point on its mass shell. The net result of this
swerving is that [214 , 316
, 316 , 396
, 396 ] a collection of particles initially with an energy-momentum
distribution
] a collection of particles initially with an energy-momentum
distribution 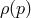 will diffuse in momentum space along their mass shell according to the equation
will diffuse in momentum space along their mass shell according to the equation
 , 396
, 396 ]
] 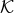 is the diffusion constant,
is the diffusion constant, 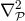 is the Laplacian in momentum space
on the mass shell of the particle,
is the Laplacian in momentum space
on the mass shell of the particle, 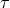 is the proper time, and
is the proper time, and 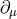 is an ordinary spacetime
derivative.
is an ordinary spacetime
derivative.
The tightest limit on  is
is  , and was obtained [316] from limits on the amount of
relic-neutrino contribution to hot dark matter. This follows from the observation that energy on the mass
shell is bound from below by the mass, so that particles close to rest, when swerving, can essentially only
increase their energy.
, and was obtained [316] from limits on the amount of
relic-neutrino contribution to hot dark matter. This follows from the observation that energy on the mass
shell is bound from below by the mass, so that particles close to rest, when swerving, can essentially only
increase their energy.
Interestingly these  -governed effects can also be relevant [396
-governed effects can also be relevant [396 ] for some of the phenomenology
already discussed in this review, concerning the threshold requirements for certain particle-physics
processes. Essentially the expected implications of swerving for these threshold analyses
is similar to that already discussed in Section 4.3.2: in any given opportunity of interaction
between a hard photon and a soft photon the swerving can effectively raise or lower (from the
perspective of the asymptotically-incoming states) the threshold requirements for pion
production. However, it appears that the bound
] for some of the phenomenology
already discussed in this review, concerning the threshold requirements for certain particle-physics
processes. Essentially the expected implications of swerving for these threshold analyses
is similar to that already discussed in Section 4.3.2: in any given opportunity of interaction
between a hard photon and a soft photon the swerving can effectively raise or lower (from the
perspective of the asymptotically-incoming states) the threshold requirements for pion
production. However, it appears that the bound 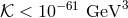 , if applicable also to
protons,33
brings the magnitude of such effects safely beyond the reach [396] of ongoing cosmic-ray studies.
, if applicable also to
protons,33
brings the magnitude of such effects safely beyond the reach [396] of ongoing cosmic-ray studies.
4.9 Tests of the equivalence principle
4.9.1 Aside on tests of the equivalence principle in the semiclassical-gravity limit
I am focusing in this review on tests motivated by (and on effects modeled within) proposals of spacetime quantization at the Planck scale, but concerning tests of the equivalence principle inspired by quantum-spacetime models there is some merit in making a small digression on tests of the equivalence principle in the semiclassical limit of quantum gravity (where, by construction, no quantum-spacetime effects could be seen). This will allow me to compellingly set-up the issue of testing the equivalence principle from a general quantum-gravity perspective and specifically from the perspective of spacetime quantization at the Planck scale.
As already discussed briefly in Section 1, there is a long tradition of phenomenological studies, concerning the semiclassical-gravity limit, based on a “gravity version” of the Schrödinger equation of the form
describing the dynamics of matter (with wave function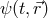 , inertial mass
, inertial mass  and gravitational mass
and gravitational mass
 ) in an external gravitational potential
) in an external gravitational potential 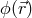 . Some of the most noteworthy results obtained within
this framework are the interferometric studies of the type first set up by Colella, Overhauser and
Werner [177], which establish that the Earth’s gravitational field is strong enough to affect the evolution of
the wave function
. Some of the most noteworthy results obtained within
this framework are the interferometric studies of the type first set up by Colella, Overhauser and
Werner [177], which establish that the Earth’s gravitational field is strong enough to affect the evolution of
the wave function 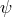 in an observably-large manner, and the more recent evidence [428
in an observably-large manner, and the more recent evidence [428 ] that
ultracold neutrons falling towards a horizontal mirror do form gravitational quantum bound
states.
] that
ultracold neutrons falling towards a horizontal mirror do form gravitational quantum bound
states.
Of relevance here is the fact that some of the issues that have been most extensively considered by
researchers involved in these studies concern the equivalence principle. This is signaled by the adoption of
separate notation for inertial and gravitational mass in Eq. (75 ). In principle the gravitational mass
). In principle the gravitational mass 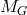 governs the accrual of gravity-induced phases, while the inertial mass
governs the accrual of gravity-induced phases, while the inertial mass 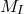 intervenes in determining the
ratio between wave vector and velocity vector in the Galilean limit (
intervenes in determining the
ratio between wave vector and velocity vector in the Galilean limit (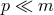 ). And even for
). And even for 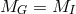 the mass does not factor out of the free-fall evolution of the quantum state (but for
the mass does not factor out of the free-fall evolution of the quantum state (but for 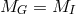 one at least
recovers [535] a complete identification between the effects of gravitation and the effects of
acceleration).
one at least
recovers [535] a complete identification between the effects of gravitation and the effects of
acceleration).
Besides neutrons, these studies can also be performed with atoms [14]. And, interestingly, one can also perform rather similar analyses in studying neutrino oscillations, finding (see, e.g., Refs. [252, 272, 148] and references therein), that gravity may induce neutrino oscillations if different neutrino flavors are coupled differently to the gravitational field, thereby violating the equivalence principle.
4.9.2 On the equivalence principle in quantum spacetime
Evidently, searches of possible violations of the equivalence principle in the semiclassical-gravity limit of quantum gravity have significant intrinsic interest. And some of these tests of the equivalence principle in semiclassical-gravity limit also find explicit motivation in approaches to the study of the full quantum-gravity problem: most notably the string-theory-inspired studies reported in Refs. [521, 195, 196, 194, 193, 192], and references therein, predict violations of the equivalence principle in the semiclassical-gravity limit.
Returning to the main subject of this review, I should stress that the idea of spacetime quantization at
the Planck scale provides a particularly crisp motivation for testing the equivalence principle. The
simplest way to see this comes from observing the role of absolute and ideally sharp locality in the
role that the equivalence principle plays in classical gravity, in contrast to the large class of
qualitatively very severe (though tiny) anomalies for locality that the various known scenarios
for spacetime quantization (starting with spacetime noncommutativity for example) provide.
Unfortunately, our present level of mastery of the relevant formalisms often falls short of allowing us to
investigate the fate of the equivalence principle. Therefore, I will briefly describe one illustrative
example of promising attempt to model how spacetime foam could affect the equivalence principle.
This is the objective of recent studies, reported in Ref. [263 ] and references therein, in which
spacetime foam is modeled in terms of small fluctuations of the metric on a given background
metric.34
The analysis of Ref. [263
] and references therein, in which
spacetime foam is modeled in terms of small fluctuations of the metric on a given background
metric.34
The analysis of Ref. [263 ], which also involves an averaging procedure over a finite spacetime scale, ends up
motivating the study of a modified Schrödinger equation of the form
], which also involves an averaging procedure over a finite spacetime scale, ends up
motivating the study of a modified Schrödinger equation of the form
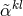 is a characterization of the spacetime foaminess, and it is natural to consider the
tensor
is a characterization of the spacetime foaminess, and it is natural to consider the
tensor 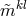 ,
as an anomalous inertial mass tensor that depends on the type of particle and on the fluctuation scenario.
The particle-dependent rescaling of the inertial mass provides a candidate key manifestation of
foam-induced violations of the equivalence principle to be sought experimentally, in ways that are once
again exemplified by the COW experiments.
,
as an anomalous inertial mass tensor that depends on the type of particle and on the fluctuation scenario.
The particle-dependent rescaling of the inertial mass provides a candidate key manifestation of
foam-induced violations of the equivalence principle to be sought experimentally, in ways that are once
again exemplified by the COW experiments.
This very recent proposal illustrates a type of path that could be followed to introduce violations of the equivalence principle originating genuinely from spacetime quantization at the Planck scale: one might find a way to describe spacetime foaminess n terms of effects of genuinely Planckian size, and then elaborate the implications of this spacetime foaminess for the equivalence principle. The formalization adopted in Ref. [263] is still too crude to allow such an explicit link between the Planck-scale picture of spacetime foam and the nature and magnitude of the effects, but provides a significant step in that direction.




![γ [xα, xβ] = iκ αβxγ (40 )](article493x.gif)
![∫ ∞ −2πiωτ Σ (ω) = −∞ dτ μ [h(t)h(t+τ)]e , (41 )](article505x.gif)


![σ2L ≃ LpT ≃ LpL [random walk case], (44 )](article536x.gif)
![2 4∕3 2∕3 σL ≃ Lp L [holography -inspired case]. (45 )](article544x.gif)
![σ2L ≃ L2p [weakest case]. (46 )](article546x.gif)
![[QG;rw] LP Σ L ≃ ω2- , (47 )](article548x.gif)
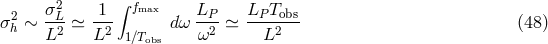
![[QG;holo] L4∕3 Σ L ≃ --P5∕3-, (49 ) ω](article553x.gif)
![[QG;weak] L2P ΣL ≃ ---, (50 ) ω](article557x.gif)
![Σ [QG;weak] ∼ 10−78 Hz −1 , Σ [QG;holo] ∼ 10−52 Hz− 1, Σ [QG;rw] ∼ 10−38 Hz −1. (51 )](article562x.gif)
![[QG] [QG ] -ΣL--- Σ = N γL2 (52 )](article578x.gif)
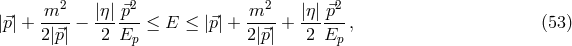

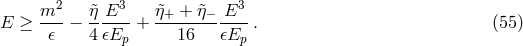




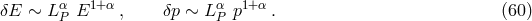


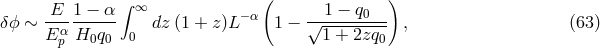
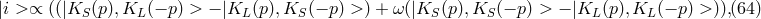

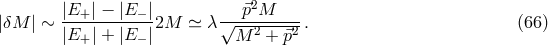
![∂tρ = i[ρ,H ] + δH ρ, (67 )](article754x.gif)
![R2π(t) = CSe −Γ St + CLe −Γ Lt + 2CI e−(Γ L+ Γ S)t∕2cos[(mL − mS )t − ϕ], (68 )](article773x.gif)

![∂tρ = i[ρ,H ] + δH ρ . (70 )](article798x.gif)
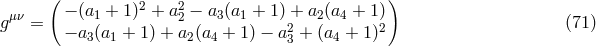
![∂tρ = i[ρ,H ]. (72 )](article805x.gif)
![[xi,xj] = 0, [x0,xi] = iχ𝜖kijnkxj , (73 )](article806x.gif)

![[ ( ) ] -1--- ⃗ 2 ∂ ψ-(t,⃗r) − 2M ∇ + MG ϕ(⃗r) ψ (t,⃗r) = i ∂t , (75 ) I](article825x.gif)
![[ ( 1 ) kl kl ] − ---- (δ + &tidle;α )∂k∂l − m ϕ(⃗r) ψ (t,⃗r) = i ∂tψ(t,⃗r), (76 ) 2m](article836x.gif)