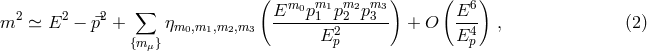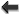1 Introduction and Preliminaries
1.1 The “Quantum-Gravity problem” as seen by a phenomenologist
Our present description of the fundamental laws of Nature is based on two disconnected pieces: “quantum
mechanics” and “general relativity”. On the quantum-mechanics side our most significant successes were
obtained applying relativistic quantum field theory, which turns out to be the appropriate formalization of
(special-) relativistic quantum mechanics. This theory neglects gravitational effects and is formulated in a
flat/Minkowskian spacetime background. Interesting results (but, so far, with little experimental support)
can be obtained by reformulating this theory in certain curved spacetime backgrounds, but there is
no rigorous generalization allowing for the dynamics of gravitational fields. The only known
way for having a manageable formulation of some gravitational effects within quantum field
theory is to adopt the perspective of effective field theory [144 , 276
, 276 ], which allows Lagrangians
that are not renormalizable. At leading order, this effective theory just gives us back Einstein’s
general relativity (GR), but beyond leading order it predicts corrections proportional to powers
of
], which allows Lagrangians
that are not renormalizable. At leading order, this effective theory just gives us back Einstein’s
general relativity (GR), but beyond leading order it predicts corrections proportional to powers
of 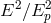 , where
, where 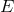 is the characteristic energy scale of the process under consideration
(typically, the center-of-mass energy for a scattering experiment) and
is the characteristic energy scale of the process under consideration
(typically, the center-of-mass energy for a scattering experiment) and 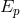 is the Planck scale
(
is the Planck scale
(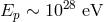 ). The effective-field-theory description evidently breaks down at energies
). The effective-field-theory description evidently breaks down at energies 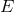 on the
order of the Planck scale, leaving unanswered [144, 276
on the
order of the Planck scale, leaving unanswered [144, 276 ] most of the core issues concerning
the interplay between gravity and quantum mechanics. Most importantly, the experiments
that have formed our trust in quantum mechanics are nearly exclusively experiments in which
gravitational effects are negligible at the presently-achievable levels of experimental sensitivity (some
of the rare instances where the outcome of a quantum-mechanical measurement is affected
by gravitational effects, such as the one reported in Ref. [428
] most of the core issues concerning
the interplay between gravity and quantum mechanics. Most importantly, the experiments
that have formed our trust in quantum mechanics are nearly exclusively experiments in which
gravitational effects are negligible at the presently-achievable levels of experimental sensitivity (some
of the rare instances where the outcome of a quantum-mechanical measurement is affected
by gravitational effects, such as the one reported in Ref. [428 ], will be discussed later in this
review).
], will be discussed later in this
review).
On the gravity side our present description is based on GR. This is a classical-mechanics theory that neglects all quantum properties of particles. Our trust in GR has emerged in experimental studies and observations in which gravitational interactions cannot be neglected, such as the motion of planets around the Sun. Planets are “composed” of a huge number of fundamental particles, and the additive nature of energy (playing in such contexts roughly the role of “gravitational charge”) is such that the energy of a planet is very large, in spite of the fact that each composing fundamental particle carries only a small amount of energy. As a result, for planets gravitational interactions dominate over other interactions. Moreover, a planet satisfies the conditions under which quantum theory is in the classical limit: in the description of the orbits of the planets the quantum properties of the composing particles can be safely neglected.
GR and relativistic quantum mechanics do have some “shared tools”, such as the notion of spacetime, but they handle these entities in profoundly different manners. The differences are indeed so profound that it might be natural to expect only one or the other language to be successful, but instead they have both been extremely successful. This is possible because of the type of experiments in which they have been tested so far, with two sharply separated classes of experiments, allowing complementary approximations.
While somewhat puzzling from a philosopher’s perspective, all this would not on its own amount to
a scientific problem. In the experiments we are presently able to perform and at the level of
sensitivities we are presently able to achieve there is no problem. But a scientific problem,
which may well deserve to be called a “quantum-gravity problem”, is found if we consider,
for example, the structure of the scattering experiments done in particle-physics laboratories.
There are no surprises in the analysis of processes with an “in” state with two particles each
with an energy of 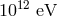 . Relativistic quantum mechanics makes definite predictions for the
(distributions/probabilities of) results of this type of measurement procedure, and our experiments fully
confirm the validity of these predictions. We are presently unable to redo the same experiments having as
“in state” two particles with energy of
. Relativistic quantum mechanics makes definite predictions for the
(distributions/probabilities of) results of this type of measurement procedure, and our experiments fully
confirm the validity of these predictions. We are presently unable to redo the same experiments having as
“in state” two particles with energy of 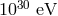 (i.e., energy higher than the Planck scale), but,
nonetheless, if one factors out gravity, relativistic quantum mechanics makes a definite prediction for
these conceivable (but presently undoable) experiments. However, for collisions of particles of
(i.e., energy higher than the Planck scale), but,
nonetheless, if one factors out gravity, relativistic quantum mechanics makes a definite prediction for
these conceivable (but presently undoable) experiments. However, for collisions of particles of
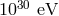 energy, the gravitational interactions predicted by GR are very strong and gravity should
not be negligible. On the other hand, the quantum properties predicted for the particles by
relativistic quantum mechanics (for example the fuzziness of their trajectories) cannot be neglected,
contrary to the “desires” of the classical mechanics of our present description of gravity. One
could naively attempt to apply both theories simultaneously, but it is well established that such
attempts do not produce anything meaningful (for example by encountering uncontrollable
divergences). As mentioned above, a framework where these issues can be raised in very precise
manner is the one of effective quantum field theory, and the break down of the effective quantum
field theory of gravitation at the Planck scale signals the challenges that are here concerning
me.
energy, the gravitational interactions predicted by GR are very strong and gravity should
not be negligible. On the other hand, the quantum properties predicted for the particles by
relativistic quantum mechanics (for example the fuzziness of their trajectories) cannot be neglected,
contrary to the “desires” of the classical mechanics of our present description of gravity. One
could naively attempt to apply both theories simultaneously, but it is well established that such
attempts do not produce anything meaningful (for example by encountering uncontrollable
divergences). As mentioned above, a framework where these issues can be raised in very precise
manner is the one of effective quantum field theory, and the break down of the effective quantum
field theory of gravitation at the Planck scale signals the challenges that are here concerning
me.
This “trans-Planckian collisions” picture is one (not necessarily the best, but a sufficiently clear)
way to introduce a quantum-gravity problem. But is the conceivable measurement procedure I
just discussed truly sufficient to introduce a scientific problem? One ingredient appears to be
missing: the measurement procedure is conceivable but presently we are unable to perform it.
Moreover, one could argue that mankind might never be able to perform the measurement
procedure I just discussed. There appears to be no need to elaborate predictions for the outcomes of
that measurement procedure. However, it is easy to see that the measurement procedure I
just discussed contains the elements of a true scientific problem. One relevant point can be
made considering the experimental/observational evidence we are gathering about the “early
Universe”. This evidence strongly supports the idea that in the early Universe particles with energies
comparable to the Planck energy scale 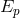 were abundant, and that these particles played
a key role in those early stages of evolution of the Universe. This does not provide us with
opportunities for “good experiments” (controlled repeatable experiments), but it does represent a
context in which proposals for the quantum-gravity/Planck-scale realm could be tested. Different
scenarios for the physical theory that applies in the quantum-gravity realm could be compared on
the basis of their description of the early Universe. The detailed analysis of a given physical
theory for the quantum-gravity realm could allow us to establish some characteristic predictions
for the early Universe and for some manifestations in our observations (cosmology) of those
early stages of evolution of the Universe. The theory would be testable on the basis of those
predictions for our present observations. Therefore, these early-Universe considerations provide an
opportunity for comparison between the predictions of a quantum-gravity theory and measurement
results. And it might not be necessary to resort to cosmology: the fact that (in setting up the
quantum-gravity problem) we have established some objective limitations of our present theories
implies that some qualitatively new effects will be predicted by the theory that applies to the
quantum-gravity realm. These effects should dominate in that realm (in particular, they will
profoundly affect the results of measurements done on particles with Planck-scale energy), but they
should always be present. For processes involving particles with energy
were abundant, and that these particles played
a key role in those early stages of evolution of the Universe. This does not provide us with
opportunities for “good experiments” (controlled repeatable experiments), but it does represent a
context in which proposals for the quantum-gravity/Planck-scale realm could be tested. Different
scenarios for the physical theory that applies in the quantum-gravity realm could be compared on
the basis of their description of the early Universe. The detailed analysis of a given physical
theory for the quantum-gravity realm could allow us to establish some characteristic predictions
for the early Universe and for some manifestations in our observations (cosmology) of those
early stages of evolution of the Universe. The theory would be testable on the basis of those
predictions for our present observations. Therefore, these early-Universe considerations provide an
opportunity for comparison between the predictions of a quantum-gravity theory and measurement
results. And it might not be necessary to resort to cosmology: the fact that (in setting up the
quantum-gravity problem) we have established some objective limitations of our present theories
implies that some qualitatively new effects will be predicted by the theory that applies to the
quantum-gravity realm. These effects should dominate in that realm (in particular, they will
profoundly affect the results of measurements done on particles with Planck-scale energy), but they
should always be present. For processes involving particles with energy 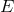 much smaller than
much smaller than
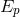 the implications of a typical quantum-gravity theory will be rather marginal but not
altogether absent. The magnitude of the associated effects should be suppressed by some small
overall coefficients, probably given by powers of the ratio
the implications of a typical quantum-gravity theory will be rather marginal but not
altogether absent. The magnitude of the associated effects should be suppressed by some small
overall coefficients, probably given by powers of the ratio 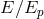 ; small but different from
zero.
; small but different from
zero.
Therefore, we do have a genuine “quantum-gravity problem”, and this problem has been studied for
more than 70 years [508 ]. Unfortunately, most of this research has been conducted assuming that no
guidance could be obtained from experiments. But, if there is to be a “science” of the quantum-gravity
problem, this problem must be treated just like any other scientific problem, seeking desperately the
guidance of experimental facts, and letting those facts take the lead in the development of new concepts.
Clearly, physicists must hope this also works for the quantum-gravity problem, or else abandon it to the
appetites of philosophers.
]. Unfortunately, most of this research has been conducted assuming that no
guidance could be obtained from experiments. But, if there is to be a “science” of the quantum-gravity
problem, this problem must be treated just like any other scientific problem, seeking desperately the
guidance of experimental facts, and letting those facts take the lead in the development of new concepts.
Clearly, physicists must hope this also works for the quantum-gravity problem, or else abandon it to the
appetites of philosophers.
It is unfortunately true that there is a certain level of risk that experiments might never give us any
clear lead toward quantum gravity, especially if we are correct in expecting that the magnitude of the
characteristic effects of the new theory should be set by the tiny Planck length (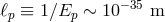 , the
inverse of the huge Planck scale in natural units). But even if the new effects were really so small
we could still try to uncover experimentally some manifestations of quantum gravity. This is
hard, and there is no guarantee of success, but we must try. As I shall stress again in later
parts of this first section, let me note here that some degree of optimism could be inspired by
considering, for example, the prediction of proton decay within certain modern grand unified theories
of particle physics. The decay probability for a proton in those theories is really very small,
suppressed by the fourth power of the ratio between the mass of the proton and the grand
unification scale (a scale that is only some three orders of magnitude smaller than the Planck
scale), but meaningful tests of scenarios for proton decay in grand unified theories have been
devised.
, the
inverse of the huge Planck scale in natural units). But even if the new effects were really so small
we could still try to uncover experimentally some manifestations of quantum gravity. This is
hard, and there is no guarantee of success, but we must try. As I shall stress again in later
parts of this first section, let me note here that some degree of optimism could be inspired by
considering, for example, the prediction of proton decay within certain modern grand unified theories
of particle physics. The decay probability for a proton in those theories is really very small,
suppressed by the fourth power of the ratio between the mass of the proton and the grand
unification scale (a scale that is only some three orders of magnitude smaller than the Planck
scale), but meaningful tests of scenarios for proton decay in grand unified theories have been
devised.
While the possibility of a “quantum gravity phenomenology” [52 ] could be considered, on
the basis of these arguments, even in the early days of quantum-gravity research, a sizable
effort has finally matured only since the second half of the 1990s. In particular, only over this
recent period do we have the first cases of phenomenological programs that truly affect the
directions taken by more formal work in quantum gravity. And, especially in relation to this healthy
two-way cross-influence between formal theory and phenomenology, a prominent role has been
played by proposals testing features that could be manifestations of spacetime quantization. The
expectation that the fundamental description of spacetime should not be given by a classical
geometry is shared by a large majority of quantum-gravity researchers. And, as a result, the
phenomenology inspired by this expectation has had influence on a sizable part of the recent
quantum-gravity literature. My goal here is primarily the one of reviewing the main results and proposals
produced by this emerging area of phenomenology centered on the possibility of spacetime
quantization.
] could be considered, on
the basis of these arguments, even in the early days of quantum-gravity research, a sizable
effort has finally matured only since the second half of the 1990s. In particular, only over this
recent period do we have the first cases of phenomenological programs that truly affect the
directions taken by more formal work in quantum gravity. And, especially in relation to this healthy
two-way cross-influence between formal theory and phenomenology, a prominent role has been
played by proposals testing features that could be manifestations of spacetime quantization. The
expectation that the fundamental description of spacetime should not be given by a classical
geometry is shared by a large majority of quantum-gravity researchers. And, as a result, the
phenomenology inspired by this expectation has had influence on a sizable part of the recent
quantum-gravity literature. My goal here is primarily the one of reviewing the main results and proposals
produced by this emerging area of phenomenology centered on the possibility of spacetime
quantization.
1.2 Quantum spacetime vs quantum black hole and graviton exchange
The notion of “quantum-gravity research” can have a different meaning for different researchers. This is due both to the many sides of the quantum-gravity problem and the fact that most researchers arrive to the study of quantum gravity from earlier interests in other areas of physics research. Because of its nature the quantum-gravity problem has a different appearance, for example, to a particle physicist and to a relativist.
In particular, this affects the perception of the implications of the “double role” of gravitational fields: unlike all other fields studied in fundamental physics the gravitational field is not just used to describe “gravitational interactions” but also characterizes the structure of spacetime itself. The structure of Einstein’s theory of gravitational phenomena tells us both of the geometry of spacetime, which should be described in terms of smooth Riemannian manifolds, and of the implications of Einstein’s equations for dynamics. But in most approaches these two sides of gravity are not handled on the same footing. Particularly from the perspective of a particle physicist it makes sense to focus on contexts amenable to treatment assuming some given Riemannian-manifold spacetime background and “gravitons” as mediators of “perturbative gravitational interactions”. Other researchers, typically not coming from a particle-physics background, are instead primarily interested in speculations for how to replace Riemannian manifolds in the description of the structure of spacetime, and contemplating a regime describing perturbative gravitational interactions is not one of their main concerns.
Because of my objectives, it is appropriate for me to locate early on in this review the quantum-spacetime issues within the broader spectrum of quantum-gravity research.
1.2.1 The quantum-black-hole regime
We do expect that there is a regime of physics where quantum gravity does not simply amount to small corrections to our currently adopted theories, but rather our current theories should be there completely inapplicable. An example of this is the class of hypothetical situations discussed in my opening remarks: if we consider a collision with impact parameter on the order of the Planck length between two particles, which exchange in the collision an energy on the order of the Planck scale, then our current theories do not even give us a reliable first approximation of the outcome.
Such collisions would create a concentration of energy comparable to the Planck scale in a region of Planck-length
size. And we have no previous experience with systems concentrated in a Planck-length region with rest
energy1
on the order of the Planck scale. In such cases, the pillars of our current description of the laws of physics
come in very explicit conflict. On one side, we have quantum mechanics, with its characteristic
property that a rest energy 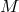 can only be localized within a region the size of the Compton
wavelength
can only be localized within a region the size of the Compton
wavelength
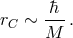
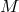 of rest energy a region of size its
Schwarzschild radius
of rest energy a region of size its
Schwarzschild radius
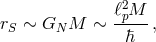
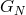 denotes Newton’s constant and
denotes Newton’s constant and 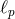 denotes the Planck length (
denotes the Planck length (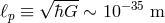 , in
units with speed-of-light scale set to unity,
, in
units with speed-of-light scale set to unity, 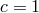 ).
).
If 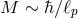 (rest energy on the order of the Planck scale), the Compton and Schwarzschild radii are of the
same order of magnitude and quantum mechanics cannot ignore gravitation but at the same time gravitation
cannot ignore quantum mechanics. Evidently we can get nowhere attempting to investigate this issue by just
combining2
somehow the Standard Model of particle physics and the general-relativistic classical description of
gravitational phenomena.
(rest energy on the order of the Planck scale), the Compton and Schwarzschild radii are of the
same order of magnitude and quantum mechanics cannot ignore gravitation but at the same time gravitation
cannot ignore quantum mechanics. Evidently we can get nowhere attempting to investigate this issue by just
combining2
somehow the Standard Model of particle physics and the general-relativistic classical description of
gravitational phenomena.
Another context of similar conceptual content can be imagined if we take for granted (which we can do only as working assumptions) the existence of Hawking radiation. We could then start with an isolated macroscopic black hole and attempt to describe its whole future evolution. As long as the black hole remains macroscopic, but loses weight through Hawking radiation, we can imagine to be able to devise a reliable first approximation. But when the black hole reaches Planck-length size (and Planck-scale rest energy) we are again left without any even approximate answers.
The description of these types of “quantum-black-hole regimes” (description that I shall use rather generically, including for example the regime characteristic of the very early Universe) is evidently an example of cases such that we could only have a satisfactory picture by understanding how both of the two roles of the gravitational fields need to be revised (how spacetime structure should be then described and how the gravitational-interaction aspects of gravitation should be then described).
Providing a description of such a quantum-black-hole regime is probably the most fascinating challenge for quantum-gravity research, but evidently it is not a promising avenue for actually discovering quantum-gravity effects experimentally. As I shall mention, somewhat incidentally in a few points of this review, this expectation would change if, surprisingly, gravitation turns out to be much stronger than we presently expect, so that at least in some contexts its strength is not characterized by the Planck scale. But this review adopts the conservative view that quantum-gravity effects are at least roughly as small as we expect, and, therefore, characterized roughly by the Planck scale. And if that is the case, it is hard to even imagine a future in which we gain access to a quantum-black-hole regime.
A key assumption of this review is that quantum gravity will manifest itself experimentally in the shape of small corrections to contexts, which we are able to describe in first approximation within our current theories.
1.2.2 The graviton-exchange regime
For particle physicists (and, therefore, for at least part of the legitimate overall perspective on the quantum-gravity problem) the most natural opportunities in which quantum gravity could introduce small corrections are in contexts involving the gravitational-interaction aspects of quantum gravity.
Rather than attempting to give general definitions let me offer a clear example. These are studies of long-range corrections to the Newtonian limit of gravitation, where gravity does look like a Newton-force interaction. By focusing on long-range features one stays far from the trouble zone mentioned in the previous Section 1.2.1. But there are still issues of considerable interest, at least conceptually, that quantum gravity should address in that regime. It is natural to expect that the description of gravity in terms of a Newton-force interaction would also show traces of the new laws that quantum gravity will bring about.
This possibility can be investigated coherently (but without any guarantee of a reliable answer) with effective-field-theory techniques applied to the nonrenormalizable theory of quantum gravity obtained by linearizing the Einstein–Hilbert theory before quantization. It essentially turns into an exercise of exploring the properties that such an effective theory attributes to gravitons. And one does derive a correction to Newton’s potential with behavior [210, 27, 329, 120, 324, 449]
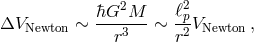
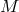 is the mass of the source of the gravitational potential and on the right-hand side I highlighted
the fact that this correction would come in suppressed with respect to the standard leading Newtonian term
by a factor given by the square of the ratio of the Planck length versus the distance scale at which the
potential is probed.
is the mass of the source of the gravitational potential and on the right-hand side I highlighted
the fact that this correction would come in suppressed with respect to the standard leading Newtonian term
by a factor given by the square of the ratio of the Planck length versus the distance scale at which the
potential is probed.
This illustrates the sort of effects one may look for within schemes centered on a background Minkowski spacetime and properties of the graviton. In this specific case the effect is unmanageably small,3 but in principle one could look for other effects of this sort that might be observably large in some applications.
1.2.3 The quantum-spacetime regime
Having given some examples of the ways in which quantum gravity might change our description of gravitational interactions, let me now turn to the complementary type of issues that are in focus when one studies the idea of spacetime quantization.
The nature of the quantum-gravity problem tells us in many ways that the ultimate description of
spacetime structure is not going to be in terms of a smooth classical geometry. We do not have
at present enough information to deduce how our formalization of spacetime should change,
but it must change. The collection of arguments in support of this expectation (see, e.g.,
Refs. [406 , 532
, 532 , 269
, 269 , 44
, 44 , 332
, 332 , 442
, 442 , 211
, 211 , 20
, 20 , 432
, 432 , 50
, 50 , 249
, 249 , 489
, 489 ]) is impressive and relies both on aspects
of the quantum-gravity problem and on analyses of proposed approaches to the solution of the
quantum-gravity problem.
]) is impressive and relies both on aspects
of the quantum-gravity problem and on analyses of proposed approaches to the solution of the
quantum-gravity problem.
Surely, some very dramatic manifestations of spacetime quantization should be expected in what I labeled as the quantum-black-hole regime. But, as already stressed above, it is hard to even imagine managing to derive evidence of spacetime quantization from experimental access to that regime. It is easy to see that our best chance for uncovering non-classical properties of spacetime is to focus on the implications of spacetime quantization for the “Minkowski limit” (or perhaps the “de Sitter limit”) of quantum gravity. Our data on contexts we presently describe as involving particle propagation in a background Minkowski spacetime is abundant and of high quality. If the fundamental formalization of spacetime is not in terms of a smooth classical geometry then we should find some traces of spacetime quantization also in those well-studied contexts. The effects are likely to be very small, but the quality of the data available to us in this quantum-spacetime regime is very high, occasionally high enough to probe spacetime structure with Planck-scale sensitivity.
This is the main theme of my review. I do not elaborate further on it here since it will take full shape in the following.
1.2.4 Aside on the classical-gravity regime
It is an interesting aspect of how the quantum-gravity community is fragmented to observe that it is sometimes difficult to explain to a relativist how graviton-exchange studies could be seen as part of quantum-gravity research and it is difficult to explain to particle physicists how studies of particles not interacting gravitationally in a quantum-spacetime can play a role in quantum-gravity research. I hope this Section proves useful in this respect.
Let me also discuss one more aspect of the interplay between quantum mechanics and gravitation that is of interest from a quantum-gravity perspective, even though at first sight it does not look like quantum gravity at all. These are studies of quantum mechanics in a curved background spacetime, without assuming spacetime is quantized and without including any graviton-like contribution to the interactions. No aspect of gravity is quantized in such studies, but they concern a regime that must be present as a limiting case of quantum gravity, and, therefore, by studying this regime we are establishing constraints on how quantum gravity might look.
On the conceptual side perhaps the most significant example of how quantum mechanics in curved
spacetime backgrounds can provide important hints toward quantum gravity is provided by
studies of black-hole thermodynamics. And it is a regime of physics where we do have some
experimental access mainly through studies of the quantum properties of particles in cases
when the geometry of spacetime near the surface of the Earth (essentially gravity of Earth, the
acceleration 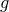 ) does matter. I shall mention a couple of these experimental studies in the next
Section 1.3.
) does matter. I shall mention a couple of these experimental studies in the next
Section 1.3.
While my focus here is on quantum-spacetime studies, it will occasionally be useful for me to adopt the perspective of quantum mechanics in curved classical background spacetimes.
1.3 20th century quantum-gravity phenomenology
In order to fully expose the change of perspective, which matured over the last decade, it is useful to first discuss briefly some earlier analyses that made contact with experiments/observations and are relevant for the understanding of the interplay between GR and quantum mechanics.
Some of the works produced by Chandrasekhar in the 1930s already fit this criterion. In particular, the renowned Chandrasekhar limit [164, 165], which describes the maximum mass of a white-dwarf star, was obtained introducing some quantum-mechanical properties of particles (essentially Pauli’s exclusion principle) within an analysis of gravitational phenomena.
A fully rigorous derivation of the Chandrasekhar limit would require quantum gravity, but not all of it: it would suffice to master one special limit of quantum gravity, the “classical-gravity limit”, in which one takes into account the quantum properties of matter fields (particles) in the presence of rather strong spacetime curvature (treated, however, classically). By testing experimentally the Chandrasekhar-limit formula, one is, therefore, to some extent probing (the classical-gravity limit of) quantum gravity.
Also relevant to the classical-gravity limit of quantum gravity are the relatively more recent studies of
the implications of the Earth’s gravitational field in matter-interferometry experiments. Experiments
investigating these effects have been conducted since the mid 1970s and are often called “COW
experiments” from the initials of Colella, Overhauser and Werner who performed the first such
experiment [177 ]. The main target of these studies is the form of the Schrödinger equation in the
presence of the Earth’s gravitational field, which could be naturally conjectured to be of the
form4
]. The main target of these studies is the form of the Schrödinger equation in the
presence of the Earth’s gravitational field, which could be naturally conjectured to be of the
form4
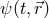 ) in the presence of the Earth’s
gravitational potential
) in the presence of the Earth’s
gravitational potential 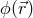 .
.
The COW experiments exploit the fact that the Earth’s gravitational potential puts together the contributions of a very large number of particles (all the particles composing the Earth) and, as a result, in spite of its per-particle weakness, the overall gravitational field is large enough to introduce observable effects.
Valuable reading material relevant for these COW experiments can be found in Refs. [484, 252 , 14
, 14 ].
While the basic message is that a gravity-improved Schrödinger equation of the form (1
].
While the basic message is that a gravity-improved Schrödinger equation of the form (1 ) is indeed
essentially applicable, some interesting discussions have been generated by these COW experiments,
particularly as a result of the data reported by one such experiment [369] (data whose reliability is still
being debated), which some authors have interpreted as a possible manifestation of a violation of the
equivalence principle.
) is indeed
essentially applicable, some interesting discussions have been generated by these COW experiments,
particularly as a result of the data reported by one such experiment [369] (data whose reliability is still
being debated), which some authors have interpreted as a possible manifestation of a violation of the
equivalence principle.
In the same category of studies relevant for the classical-gravity limit of quantum gravity I should
mention some proposals put forward mainly by Anandan (see, e.g., Ref. [77, 76]), already in the mid 1980s,
and some very recent remarkable studies that test how the gravitational field affects the structure of
quantum states, such as the study reported in Ref. [428 ] that I shall discuss in some detail later in this
review.
] that I shall discuss in some detail later in this
review.
Evidently, the study of the classical limit provides only a limited window on quantum gravity, and surely cannot provide any insight on the possibility of short-distance spacetime quantization, on which I shall focus here.
A list of early examples of studies raising at least the issue that spacetime structure might one day be
probed with Planck-scale sensitivity should start with the arguments reported by Mead in 1965 [407].
There, Mead contemplated the broadening of spectral lines possibly resulting from adopting the Planck
length as the value of the minimum possible uncertainty in position measurements. Then, in works
published in the 1980s and early 1990s, there were a few phenomenological studies, adopting the Planck
scale as target and focusing essentially on the possibility that quantum-mechanical coherence might be
spoiled by quantum-gravity effects. One example is provided by the studies of Planck-scale-induced
CPT-symmetry violation and violations of ordinary quantum mechanics reported in Refs. [219 , 220
, 220 ] and
references therein (also see, for aspects concerning mainly the CPT-symmetry aspects, Refs. [298
] and
references therein (also see, for aspects concerning mainly the CPT-symmetry aspects, Refs. [298 , 108
, 108 ]),
which are particularly relevant for the analysis of data [13
]),
which are particularly relevant for the analysis of data [13 ] on the neutral-kaon system. A
quantization of spacetime is encoded in the non-critical-string-theory formalism adopted in
Refs. [219
] on the neutral-kaon system. A
quantization of spacetime is encoded in the non-critical-string-theory formalism adopted in
Refs. [219 , 220
, 220 ], but only to the extent that one can view as such the novel description of time there
adopted. A similar characterization applies to the studies reported in Refs. [452
], but only to the extent that one can view as such the novel description of time there
adopted. A similar characterization applies to the studies reported in Refs. [452 , 453
, 453 , 454
, 454 ],
which considered violations of ordinary quantum mechanics of a type describable in terms of the
“primary-state-diffusion” formalism, with results that could be relevant for atom interferometry. Also
in Refs. [452
],
which considered violations of ordinary quantum mechanics of a type describable in terms of the
“primary-state-diffusion” formalism, with results that could be relevant for atom interferometry. Also
in Refs. [452 , 453
, 453 , 454
, 454 ] the main quantum-spacetime feature is found in the description of
time.
] the main quantum-spacetime feature is found in the description of
time.
From a broader quantum-gravity-problem perspective I should also mention the possibility of violations
of CPT and Lorentz symmetry within string theory analyzed in Refs. [347 , 345
, 345 ]. These studies, like most
phenomelogy-relevant studies inspired by string theory (see related comments later in this review), do not
involve any spacetime quantization and do not necessarily imply that the magnitude of the effects is set by
a Planckian scale. But they should nonetheless be prominently listed among the early proposals assuming
that some of the theories used in quantum-gravity research might be testable with currently-available
experimental techniques.
]. These studies, like most
phenomelogy-relevant studies inspired by string theory (see related comments later in this review), do not
involve any spacetime quantization and do not necessarily imply that the magnitude of the effects is set by
a Planckian scale. But they should nonetheless be prominently listed among the early proposals assuming
that some of the theories used in quantum-gravity research might be testable with currently-available
experimental techniques.
1.4 Genuine Planck-scale sensitivity and the dawn of quantum-spacetime phenomenology
The rather isolated proposals that composed “20th-century quantum-gravity phenomenology” were already
rather significant. In particular, some of these studies, perhaps most notably the ones in Ref. [220 ] and
Ref. [454
] and
Ref. [454 ], were providing first preliminary evidence of the fact that it might be possible to investigate
experimentally the structure of spacetime at the Planck scale, which is expected to be the main key to the
understanding of the quantum-gravity realm, and should involve spacetime quantization. But, in spite of
their objective significance, these studies did not manage to have an impact on the overall development of
quantum-gravity research. For example, all mainstream quantum-gravity reviews up to the mid 1990s still
only mentioned the “experiments issue” in the form of some brief folkloristic statements, such
as “the only way to test Planck scale effects is to build a particle accelerator all around our
galaxy”.
], were providing first preliminary evidence of the fact that it might be possible to investigate
experimentally the structure of spacetime at the Planck scale, which is expected to be the main key to the
understanding of the quantum-gravity realm, and should involve spacetime quantization. But, in spite of
their objective significance, these studies did not manage to have an impact on the overall development of
quantum-gravity research. For example, all mainstream quantum-gravity reviews up to the mid 1990s still
only mentioned the “experiments issue” in the form of some brief folkloristic statements, such
as “the only way to test Planck scale effects is to build a particle accelerator all around our
galaxy”.
The fact that up to the mid 1990s the possibility of a quantum-spacetime phenomenology was
mostly ignored, resulted in large part from a common phenomenon of “human inertia” that
affects some scientific communities, but some role was also played by a meaningful technical
observation: the studies available up to that point relied on models with the magnitude of the effect
set by a free dimensionless parameter, and at best the sensitivity of the experiment was at a
level such that one could argue setting the value of the dimensionless parameter as a ratio
between the Planck length and one of the characteristic length scales of the relevant physical
context. It is true that this kind of dimensional-analysis reasoning does not amount to really
establishing that the relevant candidate quantum-gravity effect is being probed with Planck-scale
sensitivity, and this resulted in a perception that such studies, while deserving some interest,
could not be described objectively as probes of the quantum-gravity realm. For some theorists a
certain level of uneasiness also originated from the fact that the formalisms adopted in studies
such as the ones in Ref. [220 ] and Ref. [454
] and Ref. [454 ] involved rather virulent departures from quantum
mechanics.
] involved rather virulent departures from quantum
mechanics.
Still, it did turn out that those earlier attempts to investigate the quantum-gravity problem
experimentally were setting the stage for a wider acceptance of quantum-spacetime phenomenology. The
situation started to evolve rather rapidly when in the span of just a few years, between 1997 and 2000,
several analyses were produced describing different physical contexts in which effects introduced
genuinely at the Planck sale could be tested. It started with some analyses of observations
of gamma-ray bursts at sub-MeV energies [66 , 247
, 247 , 491
, 491 ], then came some analyses of large
laser-light interferometers [51
], then came some analyses of large
laser-light interferometers [51 , 54
, 54 , 53
, 53 , 433
, 433 ], quickly followed by the first discussions of Planck
scale effects relevant for the analysis of ultra-high-energy cosmic rays [327
], quickly followed by the first discussions of Planck
scale effects relevant for the analysis of ultra-high-energy cosmic rays [327 , 38
, 38 , 73
, 73 ] and the
first analyses relevant for observations of TeV gamma rays from blazars [38
] and the
first analyses relevant for observations of TeV gamma rays from blazars [38 , 73
, 73 , 463
, 463 ] (also see
Ref. [331, 119]).
] (also see
Ref. [331, 119]).
In particular, the fact that some of these analyses (as I discuss in detail later) considered Planck-scale
effects amounting to departures from classical Lorentz symmetry played a key role in their ability to
have an impact on a significant portion of the overall quantum-gravity-research effort. Classical
Lorentz symmetry is a manifestation of the smooth (classical) light-cone structure of Minkowski
spacetime, and it has long been understood that by introducing new “quantum features” (e.g.,
discreteness or noncommutativity of the spacetime coordinates) in spacetime structure, as some
aspects of the “quantum-gravity problem” might invite us to do, Lorentz symmetry may be
affected. And the idea of having some departure from Lorentz symmetry does not necessarily
require violations of ordinary quantum mechanics. Moreover, by offering an opportunity to test
quantum-gravity theories at a pure kinematical level, these “Lorentz-symmetry-test proposals” provided a
path toward testability that appeared to be accessible even to the most ambitious theories that
are being considered as candidates for the solution of the quantum gravity problem. Some of
these theories are so complex that one cannot expect (at least not through the work of only a
few generations of physicists) to extract all of their physical predictions, but the kinematics of
the “Minkowski limit” may well be within our reach. An example of this type is provided by
Loop Quantum Gravity (LQG) [476 , 96
, 96 , 502
, 502 , 524
, 524 , 93
, 93 ], where one is presently unable to even
formulate many desirable physics questions, but at least some (however tentative) progress
has been made [247
], where one is presently unable to even
formulate many desirable physics questions, but at least some (however tentative) progress
has been made [247 , 33
, 33 , 523
, 523 , 75
, 75 , 128] in the exploration of the kinematics of the Minkowski
limit.
, 128] in the exploration of the kinematics of the Minkowski
limit.
From a pure-phenomenology perspective, the late-1990s transition is particularly significant, as I shall
discuss in greater detail later, in as much as it marks a sharp transition toward falsifiability. Some of the
late-1990s phenomenology proposals concern effects that one can imagine honestly deriving
in a given quantum-gravity theory. Instead the effects described in studies such as the ones
reported in Ref. [220 ] and Ref. [454
] and Ref. [454 ] were not really derived from proposed models but rather
they were inspired by some paths toward the solution of the quantum-gravity problem (the
relevant formalisms were not really manageable to the point of allowing a rigorous derivation of
the nature and size of the effects under study, but some intuition for the nature and size of
the effects was developed combining our limited understanding of the formalisms and some
heuristics). Such a line of reasoning is certainly valuable, and can inspire some meaningful
“new physics” experimental searches, but if the results of the experiments are negative the
theoretical ideas that motivated them are not falsified: when the link from theory to experiments is
weak (contaminated by heuristic arguments) it is not possible to follow the link in the opposite
direction (use negative experimental results to falsify the theory). Through further developments of
the work that started in the late 1990s we are now getting close to taking quantum-spacetime
phenomenology from the mere realm of searches of quantum-spacetime effects (which are striking if
they are successful but have limited impact if they fail) to the one of “falsification tests” of
some theoretical ideas. This is a point that I am planning to convey strongly with some key
parts of this review, together with another sign of maturity of this phenomenology: the ability
to discriminate between different (but similar) Planck-scale physics scenarios. In order for a
phenomenology to even get started one must find some instances in which the new-physics
effects can be distinguished from the effects predicted by current theories, but a more mature
phenomenology should also be able to discriminate between similar (but somewhat different) new-physics
scenarios.
] were not really derived from proposed models but rather
they were inspired by some paths toward the solution of the quantum-gravity problem (the
relevant formalisms were not really manageable to the point of allowing a rigorous derivation of
the nature and size of the effects under study, but some intuition for the nature and size of
the effects was developed combining our limited understanding of the formalisms and some
heuristics). Such a line of reasoning is certainly valuable, and can inspire some meaningful
“new physics” experimental searches, but if the results of the experiments are negative the
theoretical ideas that motivated them are not falsified: when the link from theory to experiments is
weak (contaminated by heuristic arguments) it is not possible to follow the link in the opposite
direction (use negative experimental results to falsify the theory). Through further developments of
the work that started in the late 1990s we are now getting close to taking quantum-spacetime
phenomenology from the mere realm of searches of quantum-spacetime effects (which are striking if
they are successful but have limited impact if they fail) to the one of “falsification tests” of
some theoretical ideas. This is a point that I am planning to convey strongly with some key
parts of this review, together with another sign of maturity of this phenomenology: the ability
to discriminate between different (but similar) Planck-scale physics scenarios. In order for a
phenomenology to even get started one must find some instances in which the new-physics
effects can be distinguished from the effects predicted by current theories, but a more mature
phenomenology should also be able to discriminate between similar (but somewhat different) new-physics
scenarios.
Together with some (however slow) progress toward establishing the ability to falsify models and
discriminate between models, the phenomenology work of this past decade has also shown that the handful
of examples of “Planck-scale sensitivities” that generated excitement between 1997 and 2000 were not a
“one-time lucky streak”: the list of examples of experimental/observational contexts in which sensitivity to
some effects introduced genuinely at the Planck scale is established (or found to be realistically within
reach) has continued to grow at a steady pace, as the content of this review will indicate, and the number of
research groups joining the quantum-spacetime-phenomenology effort is also growing rapidly. And it is not
uncommon for recent quantum-gravity reviews [91, 475 , 501, 151], even when the primary focus is on
developments on the mathematics side, to discuss in some detail (and acknowledge the significance of) the
work done in quantum-gravity phenomenology.
, 501, 151], even when the primary focus is on
developments on the mathematics side, to discuss in some detail (and acknowledge the significance of) the
work done in quantum-gravity phenomenology.
1.5 A simple example of genuine Planck-scale sensitivity
So far, my preliminary description of quantum-spacetime phenomenology has a rather abstract character. It may be useful to now provide a simple example of analysis that illustrates some of the concepts I have discussed and renders more explicit the fact that some of the sensitivity levels now available experimentally do correspond to effects introduced genuinely at the Planck scale.
These objectives motivate me to invite the reader to contemplate the possibility of
a discretization of spacetime on a lattice with 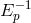 lattice spacing and a free particle
propagating on such a spacetime. It is well established that in these hypotheses there are
lattice spacing and a free particle
propagating on such a spacetime. It is well established that in these hypotheses there are
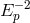 corrections to the energy-momentum on-shell relation, which in general are of the
type5
corrections to the energy-momentum on-shell relation, which in general are of the
type5
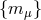 are such that
are such that 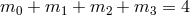 , and the parameters
, and the parameters
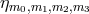 , which for
, which for 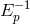 lattice spacing typically turn out to be of order 1 (when non-zero), reflect
the specifics of the chosen discretization.
lattice spacing typically turn out to be of order 1 (when non-zero), reflect
the specifics of the chosen discretization.
I should stress that the idea of a rigid-lattice description of spacetime is not really one of the most
advanced for quantum-gravity research (but see the recent related study in Ref. [114]). Moreover, while it is
easy to describe a free particle on such a lattice, the more realistic case of interacting fields is very different,
and its implications for the form of the on-shell relation are expected to be significantly more complex than
assumed in Eq. (2 ). In particular, if described within effective field theory, the implications for interacting
theories of such a lattice description of spacetime include departures from special-relativistic on-shellness for
which there is no Planck-scale suppression, and are therefore unacceptable. This is due to loop corrections,
through a mechanism of the type discussed in Refs. [455
). In particular, if described within effective field theory, the implications for interacting
theories of such a lattice description of spacetime include departures from special-relativistic on-shellness for
which there is no Planck-scale suppression, and are therefore unacceptable. This is due to loop corrections,
through a mechanism of the type discussed in Refs. [455 , 182
, 182 , 515
, 515 , 190
, 190 ] (on which I shall return
later), and assumes one is naturally unwilling to contemplate extreme fine-tuning. I feel it is
nonetheless very significant that the, however, unrealistic case of a free particle propagating in a
lattice with Planck-scale lattice spacing leads to features of the type shown in Eq. (2
] (on which I shall return
later), and assumes one is naturally unwilling to contemplate extreme fine-tuning. I feel it is
nonetheless very significant that the, however, unrealistic case of a free particle propagating in a
lattice with Planck-scale lattice spacing leads to features of the type shown in Eq. (2 ). It shows
that features of the type shown in Eq. (2
). It shows
that features of the type shown in Eq. (2 ) have magnitude set by nothing else but a feature of
Planck-scale magnitude introduced in spacetime structure. So, in spite of the idealizations involved,
the smallness of the effects discussed in this Section is plausibly representative of the type of
magnitude that quantum-spacetime effects could have, even though any realistic model of the
Standard Model of particle physics in a quantum spacetime, should evidently remove those
idealizations.
) have magnitude set by nothing else but a feature of
Planck-scale magnitude introduced in spacetime structure. So, in spite of the idealizations involved,
the smallness of the effects discussed in this Section is plausibly representative of the type of
magnitude that quantum-spacetime effects could have, even though any realistic model of the
Standard Model of particle physics in a quantum spacetime, should evidently remove those
idealizations.
One finds that in most contexts corrections to the energy-momentum relation of the type in
Eq. (2 ) are completely negligible. For example, for the analysis of center-of-mass collisions
between particles of energy
) are completely negligible. For example, for the analysis of center-of-mass collisions
between particles of energy 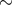 1 TeV (such as the ones studied at the LHC) these correction
terms affect the analysis at the level of 1 part in
1 TeV (such as the ones studied at the LHC) these correction
terms affect the analysis at the level of 1 part in 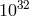 . However (at least if such a modified
dispersion relation is part of a framework with standard laws of energy-momentum conservation),
one easily finds [327
. However (at least if such a modified
dispersion relation is part of a framework with standard laws of energy-momentum conservation),
one easily finds [327 , 38
, 38 , 463
, 463 , 73
, 73 ] significant implications for the cosmic-ray spectrum. In
particular, one can consider the “GZK cutoff” (named after Greisen–Zatsepin–Kuzmin), which is
a key expected feature of the cosmic-ray spectrum, and is essentially given by the threshold
energy for cosmic-ray protons to produce pions in collisions with cosmic microwave background
radiation (CMBR) photons. In the evaluation of the threshold energy for
] significant implications for the cosmic-ray spectrum. In
particular, one can consider the “GZK cutoff” (named after Greisen–Zatsepin–Kuzmin), which is
a key expected feature of the cosmic-ray spectrum, and is essentially given by the threshold
energy for cosmic-ray protons to produce pions in collisions with cosmic microwave background
radiation (CMBR) photons. In the evaluation of the threshold energy for 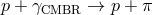 , the
, the
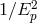 correction terms of (2
correction terms of (2 ) can be very significant. As I shall discuss in greater detail in
Section 3.5, whereas the classical-spacetime prediction for the GZK cutoff is around
) can be very significant. As I shall discuss in greater detail in
Section 3.5, whereas the classical-spacetime prediction for the GZK cutoff is around 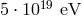 , a
much higher value of the cutoff is naturally obtained [327
, a
much higher value of the cutoff is naturally obtained [327 , 38
, 38 , 463
, 463 , 73
, 73 ] in frameworks with the
structure of Eq. (2
] in frameworks with the
structure of Eq. (2 ). The Planck-scale correction terms in Eq. (2
). The Planck-scale correction terms in Eq. (2 ) turn into corresponding
correction terms for the threshold-energy formula, and the significance of these corrections can
be roughly estimated with
) turn into corresponding
correction terms for the threshold-energy formula, and the significance of these corrections can
be roughly estimated with 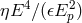 , where
, where 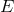 is the energy of the cosmic-ray proton
and
is the energy of the cosmic-ray proton
and  is the energy of the CMBR photon, to be compared to
is the energy of the CMBR photon, to be compared to 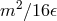 , where
, where 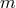 here is
the proton mass, which roughly gives the GZK scale. Adopting the “typical quantum-gravity
estimate”6
here is
the proton mass, which roughly gives the GZK scale. Adopting the “typical quantum-gravity
estimate”6
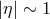 it turns out that in the GZK regime the ratio
it turns out that in the GZK regime the ratio 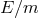 is large enough to compensate for the
smallness of the ratio
is large enough to compensate for the
smallness of the ratio 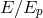 , so that a term of the type
, so that a term of the type 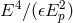 is not negligible with
respect to
is not negligible with
respect to 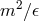 . This observation is one of the core ingredients of the quantum-spacetime
phenomenology that has been done [327
. This observation is one of the core ingredients of the quantum-spacetime
phenomenology that has been done [327 , 38
, 38 , 463
, 463 , 73
, 73 ] analyzing GZK-scale cosmic rays. Another key
ingredient of those analyses is the quality of cosmic-ray data, which has improved very significantly
over these last few years, especially as a result of observations performed at the Pierre Auger
Observatory.
] analyzing GZK-scale cosmic rays. Another key
ingredient of those analyses is the quality of cosmic-ray data, which has improved very significantly
over these last few years, especially as a result of observations performed at the Pierre Auger
Observatory.
Let me here use this cosmic-ray context also as an opportunity to discuss explicitly a first example of the
type of “amplifier” that is inevitably needed in quantum-gravity phenomenology. It is easy to figure
out [52 , 73
, 73 ] that the large ordinary-physics number that acts as amplifier of the Planck-scale effect in this
case is provided by the ratio between a cosmic-ray proton ultra-high energy, which can be of order
] that the large ordinary-physics number that acts as amplifier of the Planck-scale effect in this
case is provided by the ratio between a cosmic-ray proton ultra-high energy, which can be of order
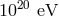 , and the mass (rest energy) of the proton. This is clearly shown by the comparison I made
between an estimate of Planck-scale corrections of order
, and the mass (rest energy) of the proton. This is clearly shown by the comparison I made
between an estimate of Planck-scale corrections of order 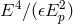 and an estimate of the uncorrected
result of order
and an estimate of the uncorrected
result of order 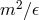 . Evidently,
. Evidently, 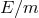 is the amplifier of the Planck-scale corrections, which also implies
that these Planck-scale modifications of the photopion-production threshold formula go very quickly from
being significant to being completely negligible, as the proton energy is decreased. A cosmic-ray proton
with energy
is the amplifier of the Planck-scale corrections, which also implies
that these Planck-scale modifications of the photopion-production threshold formula go very quickly from
being significant to being completely negligible, as the proton energy is decreased. A cosmic-ray proton
with energy 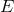 on the order of
on the order of 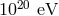 is so highly boosted that
is so highly boosted that 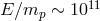 , and this
leads to
, and this
leads to 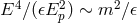 in my estimates, but at accelerator-accessible proton energies (and
proton boosts with respect to its rest frame) the correction is completely negligible. According
to traditional quantum-gravity arguments, which focus only on the role played by the ratio
in my estimates, but at accelerator-accessible proton energies (and
proton boosts with respect to its rest frame) the correction is completely negligible. According
to traditional quantum-gravity arguments, which focus only on the role played by the ratio
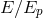 , one should assume that this analysis could be successful only when
, one should assume that this analysis could be successful only when 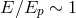 ; clearly
instead this analysis is successful already at energies of order
; clearly
instead this analysis is successful already at energies of order 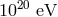 (i.e., some 8 orders of
magnitude below the Planck scale). And this is not surprising since the relevant Planck-scale
effect is an effect of Lorentz symmetry violation, so that large boosts (i.e., in this context, large
values of
(i.e., some 8 orders of
magnitude below the Planck scale). And this is not surprising since the relevant Planck-scale
effect is an effect of Lorentz symmetry violation, so that large boosts (i.e., in this context, large
values of 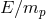 ) can act as powerful amplifiers of the effect, even when the energies are not
Planckian.
) can act as powerful amplifiers of the effect, even when the energies are not
Planckian.
1.6 Focusing on a neighborhood of the Planck scale
There are a strikingly large number of arguments pointing to the Planck scale as the characteristic scale of
quantum-gravity effects. Although clearly these arguments are not all independent, their overall
weight must certainly be judged as substantial. I shall not review them here since they can
easily be found in several quantum-gravity reviews, and there are even some dedicated review
papers (see, e.g., Ref. [249 ]). Faithful to the perspective of this review, I do want to stress one
argument in favor of the Planck scale as the quantum-gravity/quantum-spacetime scale, which
is often overlooked, but is in my opinion particularly significant, especially since it is based
(however indirectly) on experimental facts. These are the well-known experimental facts pointing
to a unification of the coupling “constants” of the electroweak forces and of the strong force.
While gravity usually is not involved in arguments that provide support for unification of the
nongravitational couplings, it is striking from a quantum-gravity perspective that, even just using the
little information we presently have (mostly at scales below the TeV scale), our present best
extrapolation of the available data on the running of these coupling constants rather robustly
indicates that there will indeed be a unification and that this unification will occur at a scale
that is not very far from the Planck scale. In spite of the fact that we are not in a position to
exclude that it is just a quantitative accident, this correspondence between (otherwise completely
unrelated) scales must presently be treated as the clearest hint of new physics that is available to
us.
]). Faithful to the perspective of this review, I do want to stress one
argument in favor of the Planck scale as the quantum-gravity/quantum-spacetime scale, which
is often overlooked, but is in my opinion particularly significant, especially since it is based
(however indirectly) on experimental facts. These are the well-known experimental facts pointing
to a unification of the coupling “constants” of the electroweak forces and of the strong force.
While gravity usually is not involved in arguments that provide support for unification of the
nongravitational couplings, it is striking from a quantum-gravity perspective that, even just using the
little information we presently have (mostly at scales below the TeV scale), our present best
extrapolation of the available data on the running of these coupling constants rather robustly
indicates that there will indeed be a unification and that this unification will occur at a scale
that is not very far from the Planck scale. In spite of the fact that we are not in a position to
exclude that it is just a quantitative accident, this correspondence between (otherwise completely
unrelated) scales must presently be treated as the clearest hint of new physics that is available to
us.
As hinted in Figure 1 , the present (admittedly preliminary) status of our understanding of this
“unification puzzle” might even suggest that there could be a single stage of full unification of all forces,
including gravity. However, according to the arguments that are presently fashionable among theoretical
physicists, it would seem that the unification of nongravitational coupling constants should occur sizably
above the scale of
, the present (admittedly preliminary) status of our understanding of this
“unification puzzle” might even suggest that there could be a single stage of full unification of all forces,
including gravity. However, according to the arguments that are presently fashionable among theoretical
physicists, it would seem that the unification of nongravitational coupling constants should occur sizably
above the scale of 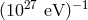 (presently preferred is a value close to
(presently preferred is a value close to 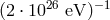 ) and at such
relatively large distance scales gravity should still be too weak to matter, since it is indeed naively expected
that gravity should be able to compete with the other forces only starting at scales as short as the Planck
length, of
) and at such
relatively large distance scales gravity should still be too weak to matter, since it is indeed naively expected
that gravity should be able to compete with the other forces only starting at scales as short as the Planck
length, of 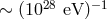 .
.
Even setting aside this coupling-unification argument, there are other compelling reasons for attributing
to the Planck scale the role of characteristic sale of quantum-gravity effects. In particular, if one adopts the
perspective of the effective-quantum-field-theory description of gravitational phenomena the case for the
Planck scale can be made rather precisely. A particularly compelling argument in this respect is found
in Ref. [276 ] which focuses on the loss of unitarity within the effective-quantum-field-theory
description of gravitational phenomena. Unitarity has been a successful criterion for determining the
scale at which other effective quantum field theories break down, such as the Fermi theory of
weak interactions. And it does turn out that the scale at which unitarity is violated for the
effective-quantum-field-theory description of gravitational phenomena is within an order of magnitude of the
Planck scale [276].
] which focuses on the loss of unitarity within the effective-quantum-field-theory
description of gravitational phenomena. Unitarity has been a successful criterion for determining the
scale at which other effective quantum field theories break down, such as the Fermi theory of
weak interactions. And it does turn out that the scale at which unitarity is violated for the
effective-quantum-field-theory description of gravitational phenomena is within an order of magnitude of the
Planck scale [276].
But it appears legitimate to consider alternatives to such estimates. For example, some authors (see,
e.g., Ref. [146 ]) consider it to be likely that the “effective Newton constant” is also affected by some
sort of renormalization-group running, and, if this is the case, then the prospects of all these
arguments would change significantly. For the length scale of spacetime quantization,
]) consider it to be likely that the “effective Newton constant” is also affected by some
sort of renormalization-group running, and, if this is the case, then the prospects of all these
arguments would change significantly. For the length scale of spacetime quantization,  , naively
assumed to be given by
, naively
assumed to be given by 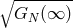 , where
, where 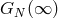 is the measured value of the Newton
constant (characteristic of gravity at large distances), any running of gravity would imply an
estimate7
of the type
is the measured value of the Newton
constant (characteristic of gravity at large distances), any running of gravity would imply an
estimate7
of the type 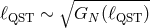 .
.
In relation to estimates of the scale of spacetime quantization these considerations should invite us to
consider the Planck length, 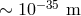 only as a crude, very preliminary estimate. Throughout
this review I shall tentatively take into account this issue by assuming that the scale where
nonclassical properties of spacetime emerge should be somewhere between
only as a crude, very preliminary estimate. Throughout
this review I shall tentatively take into account this issue by assuming that the scale where
nonclassical properties of spacetime emerge should be somewhere between 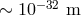 and
and
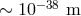 , hoping that three orders of magnitude of prudence from above and below should
suffice.
, hoping that three orders of magnitude of prudence from above and below should
suffice.
It is striking that these considerations also allow one to be more optimistic with respect to the (already
intrinsically appealing [473 ]) hypothesis of a single stage of unification of all forces, possibly even at
distance scales as “large” as
]) hypothesis of a single stage of unification of all forces, possibly even at
distance scales as “large” as 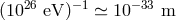 . And I find that, in relation to this issue, the recent
(mini-)burst of interest in the role of gravity in unification is particularly exciting. A convincing case is
being built concerning the possibility that gravity might affect the running of the Standard-Model coupling
constants, and this too could have significant effects for the estimate of the unification scale (see, e.g.,
Refs. [473, 529] and references therein). And in turn there is a rather robust argument (see, e.g.,
Refs. [146, 147] and references therein) suggesting that the other fields might significantly affect the
strength of gravity.
. And I find that, in relation to this issue, the recent
(mini-)burst of interest in the role of gravity in unification is particularly exciting. A convincing case is
being built concerning the possibility that gravity might affect the running of the Standard-Model coupling
constants, and this too could have significant effects for the estimate of the unification scale (see, e.g.,
Refs. [473, 529] and references therein). And in turn there is a rather robust argument (see, e.g.,
Refs. [146, 147] and references therein) suggesting that the other fields might significantly affect the
strength of gravity.
My personal perspective on the overall balance of this limited insight that is available to us is summarized by the attitude I adopted for this review in relation to the expectations for the value of the quantum-spacetime scale. Unsurprisingly, I give top priority for this to the only (and however faint) indication we have from experiments: the values measured for coupling constants at presently accessible “ultra-large” distance scales appear to be arranged in such a way as to produce a unification of nongravitational forces at a much smaller length scale, which happens to be not distant from where we would naively expect gravity to come into the picture. This in some sense tells us that our naive estimate of where gravity becomes “strong” (and spacetime turns nonclassical) cannot be too far off the mark. But at the same time imposes upon us at least a certain level of prudence: we cannot assume that the quantum-spacetime scale is exactly the Planck length, but we have some encouragement for assuming that it is within a few orders of magnitude of the Planck length.
In closing this long aside on the quantum-gravity/quantum-spacetime scale, let me stress that
even prudently assuming a few orders of uncertainty above and below the Planck length is
not necessarily safe. It is in my opinion the most natural working assumption in light of the
information presently available to us, but we should be fully aware of the fact that our naive
estimates might be off by more than a few orders of magnitude. Following the line of reasoning
adopted here this would take the shape of a solution for 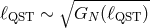 that unexpectedly
turned out to be wildly different form the Planck length. The outlook of the analysis of the
unification of forces appears to discourage such speculations, but we must be open to the possibility
that the story here summarized in Figure 1
that unexpectedly
turned out to be wildly different form the Planck length. The outlook of the analysis of the
unification of forces appears to discourage such speculations, but we must be open to the possibility
that the story here summarized in Figure 1 might just be a cruel numerical accident (more
on this toward the end of this review, when I briefly consider the “large extra dimensions”
scenario).
might just be a cruel numerical accident (more
on this toward the end of this review, when I briefly consider the “large extra dimensions”
scenario).
1.7 Characteristics of the experiments
Having commented on the first “ingredient” for the search of experiments relevant for quantum spacetime and quantum gravity, which is the estimate of the characteristic scale of this new physics, let me next comment on a few other ingredients, starting with some intuition for the type of quantum-spacetime effects that one might plausibly look for, and what that requires.
As stressed earlier in this section, we cannot place much hope of experimental breakthroughs in the full quantum-black-hole regime. Our best chances are for studies of contexts amenable to a description in terms of the properties of particles in a background quantum spacetime. And, as also already stressed, these effects will be minute, with magnitude governed by some power of the ratio between the Planck length and the wavelength of the particles involved.
The presence of these suppression factors on the one hand reduces sharply our chances of actually
discovering quantum-spacetime effects, but on the other hand simplifies the problem of figuring out what
are the most promising experimental contexts, since these experimental contexts must enjoy very special
properties that would not easily go unnoticed. For laboratory experiments, even an optimistic
estimate of these suppression factors leads to a suppression of order 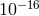 , which one obtains by
assuming (probably already using some optimism) that at least some quantum-gravity effects are
only linearly suppressed by the Planck length and taking as particle wavelength the shorter
wavelengths we are able to produce (
, which one obtains by
assuming (probably already using some optimism) that at least some quantum-gravity effects are
only linearly suppressed by the Planck length and taking as particle wavelength the shorter
wavelengths we are able to produce (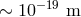 ). In astrophysics (which, however, limits one to
“observations” rather than “experiments”) particles of shorter wavelength are being studied, but even
for the highest energy cosmic rays, with energy of
). In astrophysics (which, however, limits one to
“observations” rather than “experiments”) particles of shorter wavelength are being studied, but even
for the highest energy cosmic rays, with energy of 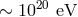 and, therefore, wavelengths of
and, therefore, wavelengths of
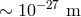 , a suppression of the type
, a suppression of the type 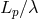 would take values of order
would take values of order 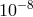 . It is mostly as a
result of this type of consideration that traditional quantum-gravity reviews considered the
possibility of experimental studies with unmitigated pessimism. However, the presence of these large
suppression factors surely cannot suffice for drawing any conclusions. Even just looking within
the subject of particle physics we know that certain types of small effects can be studied, as
illustrated by the example of the remarkable limits obtained on proton instability. The prediction of
proton decay within certain grand unified theories of particle physics is really a small effect,
suppressed by the fourth power of the ratio between the mass of the proton and grand-unification
scale, which is only three orders of magnitude smaller than the Planck scale. In spite of this
horrifying suppression, of order
. It is mostly as a
result of this type of consideration that traditional quantum-gravity reviews considered the
possibility of experimental studies with unmitigated pessimism. However, the presence of these large
suppression factors surely cannot suffice for drawing any conclusions. Even just looking within
the subject of particle physics we know that certain types of small effects can be studied, as
illustrated by the example of the remarkable limits obtained on proton instability. The prediction of
proton decay within certain grand unified theories of particle physics is really a small effect,
suppressed by the fourth power of the ratio between the mass of the proton and grand-unification
scale, which is only three orders of magnitude smaller than the Planck scale. In spite of this
horrifying suppression, of order ![[m ∕E ]4 ∼ 10− 64 proton GUT](article97x.gif) , with a simple idea we have managed to
acquire full sensitivity to the new effect: the proton lifetime predicted by grand unified theories is
of order
, with a simple idea we have managed to
acquire full sensitivity to the new effect: the proton lifetime predicted by grand unified theories is
of order 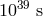 and quite a few generations of physicists should invest their entire lifetimes
staring at a single proton before its decay, but by managing to keep under observation a large
number of protons (think for example of a situation in which
and quite a few generations of physicists should invest their entire lifetimes
staring at a single proton before its decay, but by managing to keep under observation a large
number of protons (think for example of a situation in which 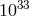 protons are monitored) our
sensitivity to proton decay is dramatically increased. In that context the number of protons is
the (ordinary-physics) dimensionless quantity that works as “amplifier” of the new-physics
effect.
protons are monitored) our
sensitivity to proton decay is dramatically increased. In that context the number of protons is
the (ordinary-physics) dimensionless quantity that works as “amplifier” of the new-physics
effect.
Outside of particle physics more success stories of this type are easily found: think for example of the Brownian-motion studies conducted a century ago. Within the 1905 Einstein description one uses Brownian-motion measurements on macroscopic scales as evidence for the atomic structure of matter. For the Brownian-motion case the needed amplifier is provided by the fact that a very large number of microscopic processes intervenes in each single macroscopic effect that is being measured.
It is hard but clearly not impossible to find experimental contexts in which there is effectively a large
amplification of some small effects of interest. And this is the strategy that is adopted [52 ] in the attempts
to gain access to the Planck-scale realm.
] in the attempts
to gain access to the Planck-scale realm.
1.8 Paradigm change and test theories of not everything
Something else that characterizes the work attitude of the community, whose results I am here reviewing, is the expectation that the solution of the quantum-gravity problem will require a significant change of theory paradigm. Members of this community find in the structure of the quantum-gravity problem sufficient elements for expecting that the transition from our current theories to a successful theory of quantum gravity should be no less (probably more) significant then the transition from classical mechanics to quantum mechanics, the prototypical example of a change of theory paradigm.
This marks a strong difference in intuition and methodology with respect to other areas of quantum-gravity research, which do not assume the need of a paradigm change. If the string theory program turned out to be successful then quantum gravity should take the shape of just one more (particularly complex but nonetheless consequential) step in the exploitation of the current theory paradigm, the one that took us all the way from QED to the Standard Model of particle physics.
This difference of intuitions even affects the nature of the sort of questions the different communities ask. The expectation of those not preparing for a change of theory paradigm is that one day some brilliant mind will wake up with the correct full quantum-gravity theory, with a single big conceptual jump. What is expected is a single big conceptual step leading to a theory that describes potentially everything we know so far.8 Something of the sort of the discovery of QCD: a full theory even though some of its answers to our questions are not immediately manifest once the theory is written out (see, e.g., confinement).
The expectation of those who are instead preparing for a change of theory paradigm is that we will get to a mature formulation of quantum gravity only at the end of a multi-step journey, with each step being of rather humble nature. The model here of is the phase of the “old quantum theory”. The change of theory paradigm in going from classical mechanics to quantum mechanics was of such magnitude that we could not possibly get it right in one single jump. Imagine someone, however brilliant, looking at black-body radiation and proposing a solution based on observables described as self-adjoint operators on Hilbert spaces and all that. Planck’s description of black-body radiation was very far from being a full formalization of quantum mechanics, and was even internally unsatisfactory, with a very limited class of contexts and regimes where it could be applied. It was a theory of very few things, but it was a necessary step toward quantum mechanics. A similar role in the gradual emergence of quantum mechanics was played by other theories of limited scope, such as Einstein’s description of the photoelectric effect, Bohr’s description of atoms, and the successful proposal by de Broglie that wave-particle duality should be applied also to matter.
So, while those not preparing for a change of paradigm look for theories of everything, we are looking for theories of very few things, like Planck, Einstein, Bohr, de Broglie and other great contributors to the ultimate advent of quantum mechanics. Let me here add that even when exploiting a successful theory paradigm, often the next level of exploitation still requires us taking some clumsy steps based on theories of few things. Consider Fermi’s description of weak interactions in terms of four-fermion-vertex processes. Fermi’s theory can be applied to a limited class of phenomena and only in a relatively narrow regime, and it is even a theory that is not satisfactory from the perspective of internal logical consistency. Yet Fermi’s theory was an important and necessary step toward richer and more satisfactory descriptions of weak interactions.
The difference in methodologies is also connected with some practical considerations, connected with the fact that the formalisms presently being considered as solutions for the quantum-gravity problem are so complex that very little is understood of their truly physical implications. Some theories of few things can even be inspired by a given theory of everything: since it is de facto impossible to compare to data present full candidates for quantum gravity one ends up comparing to data the predictions of an associated “test theory”, a model that is inspired by some features we do understand (usually not more than qualitatively or semi-quantitatively) of the original theory, but casts them within a simple framework that is well suited for comparison to experiments (but for which there is no actual guarantee of full compatibility with the original theory).
So, in the eyes of some workers these test theories of few things are needed to bridge the gap between the experimental data and our present understanding of the relevant formalisms. In the eyes of others the test theories of few things are just attempts to bridge the gap between the experimental data available to us and our limited understanding of the quantum-gravity problem.
Essentially in working in quantum-spacetime phenomenology one must first develop some intuition for some candidate quantum-spacetime effects. And this can come either from analyzing the structure of the formalisms that are being considered in the search of a solution to the quantum-gravity problem or from analyzing the structure of the quantum-gravity problem. Once a class of effects is deemed of interest some test theories of these candidate effects must be developed so that they can be used as guidance for experimental searches.
From the perspective of a phenomenologist, some carefully tailored test theories can also be valuable as some sort of common language to be used in assessing the progresses made in improving the sensitivity of experiments, a language that must be suitable both for experimentalists and for those working on the development of quantum-gravity theories.
The possibility to contemplate such “quantum-gravity theories of not everything” is facilitated by the fact that the “quantum-gravity problem” can be described in terms of several “subproblems”, each challenging us perhaps as much as some full open problems of other areas of physics. To mention just a few of these “subproblems” let me notice that: (i) it appears likely that the solution of this problem requires a nonclassical description of spacetime geometry, (ii) quantum gravity might have to be profoundly different (from an “information-theory perspective”) from previous fundamental-physics theories, as suggested by certain analyses of the evolution of pure states in a black-hole background, (iii) the perturbative expansions that are often needed for the analysis of experimental data might require the development of new techniques, since it appears that the ones that rely on perturbative renormalizability might be unavailable, and (iv) we must find some way to reconcile general-relativistic background independence with the apparent need of quantum mechanics to be formulated in a given background spacetime.
For each of these aspects of the quantum-gravity problem we can, in principle, attempt to devise formalisms, intended as descriptions of those regimes of the quantum-gravity realm that are dominantly characterized by the corresponding features.
1.9 Sensitivities rather than limits
In providing my description of the present status of quantum-spacetime phenomenology, I shall adopt as my “default mode” that of characterizing the sensitivities that are within reach for certain classes of experiments/observations, with only a few cases where I discuss both sensitivities and available experimental limits. The analysis of sensitivities was the traditional exercise a decade ago, in the early days of modern quantum-spacetime phenomenology, since the key objective then was to establish that sensitivity to effects introduced genuinely at the Planck scale is achievable. In light of the observation I already reported in Section 1.5 (and several other observations reported later in this review), the “case for existence” of quantum-spacetime phenomenology is at this point well settled.
We are now entering a more mature phase in which we start having the first examples of candidate quantum-spacetime effects for which the development of suitable test theories is approaching a level of maturity such that placing experimental bounds (“limits”) on the parameters of these test theories does deserve intrinsic interest. However, at the time of writing, the transition “from sensitivities to limits” is not yet complete. The cases where I will offer comments on available experimental limits are cases for which (in my opinion) this transition has been made satisfactorily. But in several areas of quantum-spacetime phenomenology it is still common practice to discuss experimental bounds on the basis of a single little-understood experimental result (often a single observation in astrophysics) and most of the test theories are not yet developed to the point that we can attach much significance to placing limits on their parameters. This is a key issue, and throughout this review I will find opportunities to discuss in more detail my concerns and offer some remarks that are relevant for completing the needed transition “from sensitivities to limits”. I do plan to regularly update this review, and with each update readers should find the emphasis gradually going more and more from sensitivities to experimental limits.
1.10 Other limitations on the scope of this review
After having clarified that the “default mode” of this review provides descriptions of sensitivities (with
occasional characterizations of experimental bounds), I should comment on the types of theory
and phenomenology that are the main focus of this review. I have prepared other reviews on
these and related topics [52 , 62
, 62 ] with a broader perspective but much more limited depth.
Here my main focus is to analyze and review in some detail the healthy interface between pure
theory and phenomenology of quantum spacetime. I shall mostly describe the phenomenology
proposals, but the selection of which proposals should be included is primarily based on their proven
ability to motivate developments on the pure-theory side and to react to (take into account
adaptively of) the indications that then emerge from these pure-theory studies. This will be the
“default mode” of my selection of topics, with some exceptions allowed in cases where I find that
there are promising opportunities for such a healthy interface to mature over the next few
years.
] with a broader perspective but much more limited depth.
Here my main focus is to analyze and review in some detail the healthy interface between pure
theory and phenomenology of quantum spacetime. I shall mostly describe the phenomenology
proposals, but the selection of which proposals should be included is primarily based on their proven
ability to motivate developments on the pure-theory side and to react to (take into account
adaptively of) the indications that then emerge from these pure-theory studies. This will be the
“default mode” of my selection of topics, with some exceptions allowed in cases where I find that
there are promising opportunities for such a healthy interface to mature over the next few
years.
The net result of these goals of the review produces a certain bias toward proposals for quantum spacetime, which originated from (or were inspired by) the study of LQG and/or the study of Planck-scale spacetime noncommutativity. These are the two areas of pure-theory research in which, so far, the desirable two-way interface has most concretely materialized: pure-theory specialists have redirected part of their work toward the topics that phenomenologists have highlighted as most promising for phenomenology; and the work of quantum-spacetime phenomenologists has been in turn influenced by the results then obtained on the pure-theory side.
In addition to a relatively long list of proposals inspired by LQG and/or by Planck-scale spacetime noncommutativity, I shall also comment on a few proposals inspired by other approaches to spacetime quantization (e.g., Causal Sets and Noncritical String Theory). From a broader quantum-gravity-problem perspective one should also consider critical string theory, which actually remains the most studied candidate for quantum gravity. However, I focus here on quantum-spacetime effects and effects whose natural characteristic scale is the Planck scale, whereas the phenomenology proposals so far inspired by the critical-string-theory research program do not revolve around quantum properties of spacetime and often the characteristic scale of the effects is not naturally the Planck scale.
I shall observe in Section 2.1.1 that the analysis of critical string theory actually has provided encouragement for the idea that it could also be a model of spacetime quantization, but the relevant aspects of critical string theory are still poorly understood and have not produced phenomenological proposals of the sort I am here reviewing. I do believe that it is likely that in a not-so-distant future some new opportunities for quantum-spacetime phenomenology will arise from this avenue.
1.11 Schematic outline of this review
The main objective of the next Section 2 is to motivate a list of candidate quantum-spacetime effects, on the basis of the structure of the quantum-gravity problem and/or of results obtained in certain theories that are being considered as relevant to the understanding of the quantum-gravity problem. The rest of this review attempts to describe the status of searches of these candidate quantum-spacetime effects.
Choosing what structure to give to Sections 3, 4, 5 and 6 was the main challenge faced by my work on this review. The option that finally prevailed attempts to assign each phenomenological proposal to a certain area of quantum-spacetime phenomenology. These should be viewed only as tentative assignments, or at least assignments based on a perception of what could be the primary targets of a given phenomenological proposal. And there are some visible limitations: some readers could legitimately argue that a certain subsection that I placed in one of the sections should instead find a more fitting setting in another section. Indeed, as I was working on this review, there were a few subsections that kept switching from one section to another. If used wisely, I feel that the structure I gave is still preferable to some of the alternatives that could have been considered. For example, even such a tentative structure of organization is probably going to be more easy to use than a long unstructured list of all the many phenomenological proposals I am considering. And the option of organizing phenomenological proposals on the basis of the theories that motivate them, rather than roughly on the basis of their primary area of relevance in phenomenology, would have been against the whole spirit of this review.
Section 3 focuses on effects that amount to Planck-scale departures from Lorentz/Poincaré symmetry,
which is the type of effects on which the most energetic quantum-spacetime phenomenology effort has
been so far directed. The content of Section 3 has some overlap with [395 ] that describes the
status of modern tests of Lorentz symmetry, and, therefore, is in part also devoted to cases in
which such tests are motivated by quantum-spacetime research. However, my perspective will
be rather different, focused on the quantum-spacetime-motivated searches and also using the
example of Lorentz/Poincaré-symmetry tests to comment on the level of maturity reached
by quantum-spacetime phenomenology in relation to the falsification of (test) theories and
to the discrimination between different but similar theories. And whereas from the broader
viewpoint of probing the robustness of Lorentz symmetry one should consider as significant any
proposal capable of improving the bounds established within a given parametrization of departures
from Lorentz symmetry, I shall focus on the demands of Planck-scale sensitivity, as required by
the objectives of research on Planck-scale quantization of spacetime, that is my main focus
here.
] that describes the
status of modern tests of Lorentz symmetry, and, therefore, is in part also devoted to cases in
which such tests are motivated by quantum-spacetime research. However, my perspective will
be rather different, focused on the quantum-spacetime-motivated searches and also using the
example of Lorentz/Poincaré-symmetry tests to comment on the level of maturity reached
by quantum-spacetime phenomenology in relation to the falsification of (test) theories and
to the discrimination between different but similar theories. And whereas from the broader
viewpoint of probing the robustness of Lorentz symmetry one should consider as significant any
proposal capable of improving the bounds established within a given parametrization of departures
from Lorentz symmetry, I shall focus on the demands of Planck-scale sensitivity, as required by
the objectives of research on Planck-scale quantization of spacetime, that is my main focus
here.
In Section 4, I describe the status of other areas of quantum-spacetime phenomenology in which the Planck-scale also characterizes the onset of ultraviolet effects, but not of the types that require departures from Lorentz/Poincaré symmetry.
While the primary objectives of this review are the ultraviolet effects linked with the Planck-scale structure of spacetime, in Section 5 I briefly consider the possibility of ultraviolet/infrared (UV/IR) mixing. In such UV/IR-mixing scenarios the role of the Planck scale would be in governing the UV side, and possibly then combining with other scales when IR effects are considered.
Sections 3, 4, and 5 concern proposals of (only a few) controlled laboratory experiments and (several) observations in astrophysics. These are the contexts in which currently one finds more mature proposals, particularly concerning the robustness of claims of Planck-scale sensitivity of some relevant data analyses. However, observations in cosmology should also provide some very valuable opportunities, and there are some “quantum-spacetime-cosmology” proposals, to which I devote Section 6, that can already be used to expose the great potential reach of this type of analyses.
While different proposals of quantum-spacetime phenomenology often involve different formalizations and completely different experimental techniques, there is a common setup of all proposals described in Sections 3, 4, 5, and 6. This main strategy of quantum-spacetime phenomenology is summarized in Section 7 , also pondering what might be some of its limitations.
Section 8 offers some closing remarks.

![[ ( 1 ) 2 ] ∂ ψ (t,⃗r) − 2-M-- ⃗∇ + MG ϕ (⃗r) ψ(t,⃗r) = i---∂t--- (1 ) I](article30x.gif)