List of Footnotes
| 1 | For simplicity, I am assuming the description of the collision is being given in the center-of-mass frame. For example, we might have two identical particles, which in that frame have the same gigantic energy but propagate in opposite directions. | |
| 2 | Note, however, that this type of Heisenberg-microscope-type issues can be studied in some of the frameworks under consideration for the quantum-gravity problem. In particular, this has attracted some interest by proponents of asymptotic safety, as illustrated by the study reported in Ref. [451] (for an alternative perspective see Ref. [216]). | |
| 3 | Our familiarity with the Newtonian regime of gravity extends down to distance scales no shorter than  ,
so the factor ,
so the factor 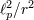 would invite us to determine a Newtonian potential with accuracy of at least parts in would invite us to determine a Newtonian potential with accuracy of at least parts in
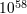 . . |
|
| 4 | Consistent with what is done in the relevant literature, I write Eq. (1 ) without assuming exact validity of the equivalence
principle, and, therefore, introduce different symbols ) without assuming exact validity of the equivalence
principle, and, therefore, introduce different symbols 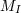 and and 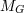 for the inertial and gravitational mass
respectively. for the inertial and gravitational mass
respectively. |
|
| 5 | For a detailed discussion of the implications for the energy-momentum relation of a given scheme of spacetime discretization see, e.g., Ref. [517]. | |
| 6 | 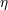 represents one of (or a linear combination of) the coefficients represents one of (or a linear combination of) the coefficients  . The quantum-gravity intuition for . The quantum-gravity intuition for 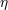 is is
 . For example, in my simple-minded “spacetime-lattice picture” . For example, in my simple-minded “spacetime-lattice picture” 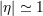 is obtained when the lattice spacing is
exactly is obtained when the lattice spacing is
exactly 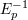 . Sensitivity to values of . Sensitivity to values of 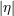 even smaller than 1 would reflect the ability to probe spacetime structure down to
distance scales even smaller than the Planck length (in the “spacetime-lattice picture” this would correspond to a lattice
spacing of even smaller than 1 would reflect the ability to probe spacetime structure down to
distance scales even smaller than the Planck length (in the “spacetime-lattice picture” this would correspond to a lattice
spacing of 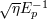 ). ). |
|
| 7 | Evidently, this might mean that the length scale of spacetime quantization might be somewhat lower or somewhat higher
than the Planck scale. But notice that when reasoning in terms of  one should then allow for the
possibility that there might not be any spacetime quantization after all (the self-consistent solution of one should then allow for the
possibility that there might not be any spacetime quantization after all (the self-consistent solution of 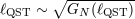 might be
might be 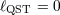 ). ). |
|
| 8 | Some colleagues even use the expression “theory of everything” without adding “we know so far”. | |
| 9 | One may then argue that there are some indirect reasons why the Planck scale should appear in formulas setting the significance of the effects, but the connection with the Planck scale remains relatively weak. | |
| 10 | While the type of quantum-spacetime effects considered in the LQG literature makes it natural to question the fate of Lorentz symmetry in the quasi-Minkowski limit, I should stress that at present no fully robust result is available, and some authors (notably Refs. [478, 479]) have observed that there could be ways to reconcile what is presently known about LQG with the presence of exact Lorentz symmetry in the quasi-Minkowski limit. | |
| 11 | A space with some elements of quantization/discreteness may have classical continuous symmetries, but only if things are arranged in an ad hoc manner. Typically quantization/discretization of spacetime observables does lead to departures from classical spacetime symmetries. So clearly spacetime-symmetry tests should be a core area of quantum-spacetime phenomenology, but to be pursued with the awareness that spacetime quantization does not automatically affect spacetime symmetries (it typically does but not automatically). | |
| 12 | In the case of canonical noncommutativity, evidence of some departures from Poincaré symmetry are
found both if 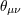 is a fixed tensor [213 is a fixed tensor [213 , 516 , 516 ] and if it is a fixed observer-independent matrix [161, 236, 100].
The possibility to preserve classical Poincaré symmetry is instead still not excluded in what was actually the
earliest approach [211 ] and if it is a fixed observer-independent matrix [161, 236, 100].
The possibility to preserve classical Poincaré symmetry is instead still not excluded in what was actually the
earliest approach [211 ] based on ] based on ![[xμ,xν] = i𝜃μν](article106x.gif) , where for , where for 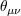 one seeks a formulation with richer algebraic
properties. one seeks a formulation with richer algebraic
properties. |
|
| 13 | While I shall not discuss it here, because it has so far attracted little interest from a quantum-spacetime perspective, I
should encourage readers to also become acquainted with the fact that studies such as the ones in Refs. [196 , 192 , 192 ],
through the mechanism for violation of the equivalence principle, also provide motivation for “varying coupling
constants” [531, 394]. ],
through the mechanism for violation of the equivalence principle, also provide motivation for “varying coupling
constants” [531, 394]. |
|
| 14 | Think of the limitations that the speed-of-light limit imposes on certain setups for clock synchronization and of the contexts in which it is impossible to distinguish between a constant acceleration and the presence of a gravitational field. | |
| 15 | And this assessment does not improve much upon observing that exact supersymmetry could protect from the emergence of any energy density of the sort relevant to such cosmological-constant studies. In fact, nature clearly does not have supersymmetry at least up to the TeV scale, and this would still lead to a natural prediction of the cosmological constant, which is some 60 orders of magnitude too high. | |
| 16 | As stressed earlier in this section, one can restore a relativistic formulation by appropriately matching the modification of the dispersion relation and a modification of energy-momentum conservation. When the modifications of the dispersion relation and of energy-momentum conservation (even when both present) do not match, one has a framework that requires a preferred frame. | |
| 17 | While Myers and Pospelov have the merit of alerting the community to several opportunities and issues within a simple model, we now understand that many of these aspects uncovered through their simple model (such as birefringence) are common aspects of a more general class of field-theory models with rotationally-invariant operators of odd dimension (see, e.g., Ref. [337]). | |
| 18 | While some observers understandably argue that the the residual grey areas that I discuss force us to still be extremely
prudent, even at the present time one could legitimately describe as robust [62 ] the observational evidence
indicating that some ] the observational evidence
indicating that some  -rays with energies up to 20 TeV are absorbed by the IR diffuse extragalactic background.
And some authors (see, e.g., Ref. [511]) actually see in the presently-available data an even sharper level of
agreement with the classical-spacetime picture, which would translate in having already achieved Planck-scale
sensitivity. -rays with energies up to 20 TeV are absorbed by the IR diffuse extragalactic background.
And some authors (see, e.g., Ref. [511]) actually see in the presently-available data an even sharper level of
agreement with the classical-spacetime picture, which would translate in having already achieved Planck-scale
sensitivity. |
|
| 19 | It used to be natural to expect [111] that indeed the highest energy cosmic rays are protons. However, this is changing
rather rapidly in light of recent dedicated studies using Auger data [7, 242 , 509 , 509 ], which favor a significant contribution from
heavy nuclei. The implications for the Lorentz symmetry analysis of the differences between protons and heavy nuclei, while
significant in the detail (see, e.g., Ref. [488]), are not as large as one might naively expect. This is due to the fact that it just
happens to be the case that the photodisintegration threshold is reached when the energy of typical heavy nuclei, such as Fe,
is ], which favor a significant contribution from
heavy nuclei. The implications for the Lorentz symmetry analysis of the differences between protons and heavy nuclei, while
significant in the detail (see, e.g., Ref. [488]), are not as large as one might naively expect. This is due to the fact that it just
happens to be the case that the photodisintegration threshold is reached when the energy of typical heavy nuclei, such as Fe,
is 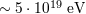 , i.e., just about the value of the photopion-production threshold, expected for cosmic-ray
protons. , i.e., just about the value of the photopion-production threshold, expected for cosmic-ray
protons. |
|
| 20 | We are dealing again with the limitations that pure-kinematics particle-reaction analyses suffer when the properties of the
incoming particles are not fully under control. The pure kinematics of the PKV0 test theory definitely forbids (for negative
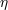 of order 1 and of order 1 and 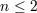 ) pion production resulting from collisions between a ) pion production resulting from collisions between a 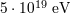 proton and a
CMBR photon. But it allows pion production resulting from collisions between a proton and a
CMBR photon. But it allows pion production resulting from collisions between a 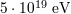 proton and
more energetic photons, and in order to exclude that possibility one ends up formulating assumptions about
dynamics (the low density of relevant photons may be compensated for by an unexpected increase in cross
section). proton and
more energetic photons, and in order to exclude that possibility one ends up formulating assumptions about
dynamics (the low density of relevant photons may be compensated for by an unexpected increase in cross
section). |
|
| 21 | For the related subject of the description of light propagation in models of emergent spacetime, see, e.g., Ref. [275] and references therein. | |
| 22 | Up to 1997, the distances from gamma-ray bursts to Earth were not established experimentally. Starting with the 1997
result of Ref. [188], we are now able to establish, through a suitable analysis of the gamma-ray-burst “afterglow”, the distance
between the gamma-ray bursts and Earth for a significant portion of all detected bursts. Sources at a distance of 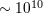 light years (
light years (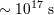 ) are not uncommon. ) are not uncommon. |
|
| 23 | There are ordinary-physics effects that could be relevant for these analyses, such as ordinary electromagnetic dispersion,
but it is easy to show [66 , 132] that already at energies of a few GeV these ordinary-physics effects would be negligible with
respect to the candidate quantum-gravity effect here considered. , 132] that already at energies of a few GeV these ordinary-physics effects would be negligible with
respect to the candidate quantum-gravity effect here considered. |
|
| 24 | Also noteworthy is the analysis reported in Ref. [156], which argues that neutrino oscillations may play a role for other aspects of quantum-spacetime phenomenology, in addition to their use in relation to flavor-dependent Planck-scale modifications of the dispersion relation. | |
| 25 | This is in part due to the fact that “naive quantum gravity” is not a renormalizable theory, and as a result the restriction to power-counting renormalizable correction terms (which is standard outside quantum-gravity research) is expected not to be necessarily applicable to quantum-gravity research. | |
| 26 | A warning to readers: whereas originally the denomination “Standard Model Extension” was universally used to describe a
framework implementing the restriction to powercounting-renormalizable correction terms, recently (see, e.g., Ref. [123 ]) some
theorists describe as “Standard Model Extension” the generalization that includes correction terms that are not powercounting
renormalizable, while they describe as a “Minimal Standard Model Extension” the case with the original restriction to
powercounting-renormalizable correction terms. Still, even as I write this review, many authors (in particular the near totality
of experimentalists involved in such studies) continue to adopt the original description of the “Standard Model
Extension”, restricted to powercounting-renormalizable correction terms, and this may create some confusion
(for example experimentalists reporting results on the “Standard Model Extension” are actually, according to
the terminology now used by some theorists, describing experimental limits on the “Minimal Standard Model
Extension”). ]) some
theorists describe as “Standard Model Extension” the generalization that includes correction terms that are not powercounting
renormalizable, while they describe as a “Minimal Standard Model Extension” the case with the original restriction to
powercounting-renormalizable correction terms. Still, even as I write this review, many authors (in particular the near totality
of experimentalists involved in such studies) continue to adopt the original description of the “Standard Model
Extension”, restricted to powercounting-renormalizable correction terms, and this may create some confusion
(for example experimentalists reporting results on the “Standard Model Extension” are actually, according to
the terminology now used by some theorists, describing experimental limits on the “Minimal Standard Model
Extension”). |
|
| 27 | Interestingly, this simple scheme for modeling spacetime-foam effects also provides the basis for the proposal put forward in Refs. [25, 24] of a mechanism that could be responsible for the cosmological matter-antimatter asymmetry. | |
| 28 | Since modern interferometers were designed to look for classical gravity waves (gravity waves are their sought “signal”), it is reasonable to denominate as “noise” all test-mass-distance fluctuations that are not due to gravity waves. I adopt terminology that reflects the original objectives of modern interferometers, even though it is somewhat awkward for the type of quantum-spacetime-phenomenology studies discussed, in which interferometers would be used for searches of quantum-gravity-induced distance fluctuations (and, therefore, in these studies quantum-gravity-induced distance fluctuations would play the role of “signal”). | |
| 29 | While most formulas in this review adopt 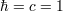 conventions, I do make some exceptions (with explicit conventions, I do make some exceptions (with explicit 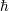 or or  )
when I believe it can help to characterize the conceptual ingredients of the formula. )
when I believe it can help to characterize the conceptual ingredients of the formula. |
|
| 30 | The fact that, according to some of these test theories, quantum-spacetime-induced noise becomes increasingly significant
as the characteristic frequency of observation is lowered, also opens the way to possible studies [492] using
cryogenic resonators, which are rigid optical interferometers with good sensitivities down to frequencies of about
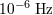 . . |
|
| 31 | The interplay between violations of Lorentz symmetry and violations of CPT symmetry, which is a part of the objectives being pursued within the context provided by the Standard Model Extension, is also the subject of a lively debate, as can be seen from Refs. [265, 160]. | |
| 32 | In Ref. [541] the main focus was again on atom interferometry, but following a closely related approach the very recent
Ref. [542 ] made a proposal for Bose–Einstein condensates. ] made a proposal for Bose–Einstein condensates. |
|
| 33 | It is not implausible that different particles would be characterized by different values of 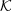 . This in particular could
reflect the expectation that more pointlike particles, such as neutrinos, should be more sensitive to the spacetime-lattice
structure with respect to composite particles (such as protons and, even more evidently, atoms). However, it appears natural to
assume [396 . This in particular could
reflect the expectation that more pointlike particles, such as neutrinos, should be more sensitive to the spacetime-lattice
structure with respect to composite particles (such as protons and, even more evidently, atoms). However, it appears natural to
assume [396 ], at least in these first explorations of causal-set phenomenology, that different particles would have values of ], at least in these first explorations of causal-set phenomenology, that different particles would have values of 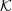 that are not too far apart.
that are not too far apart. |
|
| 34 | Similar types of “fuzzy metrics” were considered in Refs. [206 , 557 , 557 , 460 , 460 ] but I postpone their discussion to Section 6.2
devoted to quantum-spacetime cosmology. ] but I postpone their discussion to Section 6.2
devoted to quantum-spacetime cosmology. |
|
| 35 | For example, for Planck-length radii one might even imagine to satisfy the Bekenstein–Hawking bound 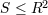 in a
theory where entropy actually scales with a cubic law of the type in a
theory where entropy actually scales with a cubic law of the type 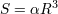 , if the proportionality parameter , if the proportionality parameter  is such that is such that
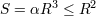 . But evidently for any such . But evidently for any such 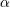 there are values of the radius large enough that instead the
Bekenstein–Hawking bound would be violated. there are values of the radius large enough that instead the
Bekenstein–Hawking bound would be violated. |
|
| 36 | I set aside here, as in Refs. [155 , 69 , 69 ], the possibility of a helicity dependence [34 ], the possibility of a helicity dependence [34 ] on the effects. ] on the effects. |
|
| 37 | There is no consistent adoption of conventions for notation in Refs. [33, 34, 154 , 155 , 155 , 69 , 69 ]. I am adopting here a notation
that appears to render more transparent the connection between arguments for UV/IR mixing from LQG and arguments for
UV/IR mixing from spacetime noncommutativity. ]. I am adopting here a notation
that appears to render more transparent the connection between arguments for UV/IR mixing from LQG and arguments for
UV/IR mixing from spacetime noncommutativity. |
|
| 38 | As already stressed, this is not necessarily a natural expectation. In particular, several arguments appear to suggest that composite particles may be less sensitive to quantum-spacetime effects than “fundamental” particles. Still, it is interesting to study this issue experimentally, and a way to do that is to look for opportunities for the “universality assumption” to break down. | |
| 39 | I am describing the analysis of Ref. [154 ] using the notation I adopted throughout this section. Instead of ] using the notation I adopted throughout this section. Instead of 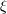 Ref. [154]
used a parameter Ref. [154]
used a parameter 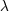 linked to linked to 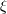 by by 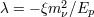 . . |
|
| 40 | Though not relevant to my review, it is interesting to note that, besides constraining certain quantum pictures of
spacetime, the measurement results reported in Refs. [428 , 429 , 429 ] can also be used to set an upper limit for an additional
short-range fundamental force [429 ] can also be used to set an upper limit for an additional
short-range fundamental force [429 ]. ]. |

