6 Quantum-Spacetime Cosmology

In the previous Sections 3, 4, 5, I discussed several opportunities for investigating candidate quantum-spacetime effects through observations in astrophysics and, occasionally, some controlled laboratory setups. However, it is likely that gradually cosmology will acquire more and more weight in the search for manifestations of quantum-spacetime effects. In the earliest stages of evolution of the Universe, the typical energies of particles were much higher than the ones we can presently achieve, and high-energy particles are the ideal probes for the short-distance structure of spacetime. Over these past few years, several studies that could be viewed as preparing the ground for this use of cosmology have been presented in the literature. Most of these proposals do not have the structure and robustness necessary for actual phenomenological analyses, such as the ones setting bounds on the parameters of a given quantum-spacetime picture. But the overall picture emerging from these studies confirms the expectation that cosmology has the potential to be a key player in quantum-spacetime phenomenology.

For a combination of reasons, I shall review this recent literature in an even more sketchy way than other parts of this review. This reflects the fact that I view this area as still at a very early stage of development: we are probably just starting to learn what could be the observable manifestations of the quantization of spacetime in cosmology. Even in cases when the quantum-spacetime side is reasonably well understood, the study of the implications for cosmology, when focused on possible observably-large manifestations, is still in its infancy. Moreover, most of the work done so far in this area does not even invoke a definite role for spacetime quantization, which is the main focus of this review, but rather finds inspiration in generic features of the quantum-gravity problem, or relies on string theory (which, as stressed, is a fully legitimate quantum-gravity candidate, but is one such candidate that, as presently understood, would rather lead us to assume that quantum properties of spacetime are absent/negligible).

In light of these considerations, the list of proposals and ideas that composes this section is not representative of the list of scenarios being considered in quantum-spacetime cosmology. It mainly serves the purpose of offering some illustrative examples of how one might go about proposing a quantum-spacetime-cosmology scenario and giving some strength to my opening remarks foreseeing a great future for quantum-spacetime cosmology.

In the last Section 6.5, I briefly mention some examples of quantum-gravity-cosmology proposals, which in their present formulation do not invoke a role for the quantization of spacetime (but could inspire future reformulations centered on a quantum-spacetime perspective).

6.1 Probing the trans-Planckian problem with modified dispersion relations

In the long run, one of the most significant opportunities for quantum-spacetime phenomenology could be an aspect of quantum-spacetime cosmology: the trans-Planckian problem. Inflation works in such a way that some of the scales that are presently of cosmological interest should have been trans-Planckian scales at the beginning of inflation, and, therefore, cannot be handled satisfactorily without (the correct) quantum gravity [134, 393, 197]. In extrapolating the evolution of cosmological perturbations according to linear theory to very early times, we are implicitly making the assumption that the theory remains perturbative to arbitrarily-high energies. And it is easy to see that the expected new physics at the Planck scale could affect our predictions. For example, if there was a sharp Planck-scale cutoff in the theory, then, if inflation lasts many e-folding, the modes which represent fluctuations on galactic scales today would not be present [134] in the theory since their wavelength would have been smaller than the cutoff length at the beginning of inflation.

While in the long run this might get very exciting, I feel we are at present only at a very early stage of exploration of the potentialities of this opportunity for quantum-spacetime phenomenology. But there is growing awareness of this opportunity and the related literature starts to grow large (see, e.g., Refs. [393, 197, 435, 136, 320, 172, 410, 217, 266, 198, 321, 145, 274, 510, 383, 135], and references therein). Many of these studies [136, 172, 410, 217, 266, 198, 321, 274] have probed the possibility that a short-distance cutoff might leave a trace in cosmology measurements such as the ones conducted on the cosmic microwave background.

Among the scenarios that have so far been considered in relation to the trans-Planckian problem, the ones that are more directly linked with the study of spacetime quantization are those involving Planck-scale modifications of the dispersion relation (see, e.g., Refs. [383, 32, 382]). For example, one may consider the possibility [32] of dispersion relations with a trans-Planckian branch, where energy increases with decreasing momenta, such as

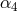for appropriate choices of the parameters and 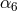. A radiation-dominated Universe with particles governed by such modified dispersion relations ends up being characterized [32] by negative radiation pressure and remarkably may be governed by an inflationary equation of state, even without introducing an inflaton field.

These results (and those of Refs. [248, 318, 437, 273]) establish a connection with previous attempts at replacing inflation by scenarios accommodating departures from Lorentz symmetry, such as the scenario with a time-varying speed of light, introduced in works by Moffat [419] and in works by Albrecht and Magueijo [30] (see also Ref. [104]). By postulating an appropriate time variation of the speed of light one can affect causality in a way that is somewhat analogous to inflation: very distant regions of the Universe, which could have never been in causal contact with a time-independent speed of light, could have been in causal contact at very early times if at those early times the speed of light was much higher than at the present time. As argued in the recent review given in Ref. [385], this alternative to inflation is rather severely constrained but still to be considered a viable alternative to inflation.

6.2 Randomly-fluctuating metrics and the cosmic microwave background

Also relevant for cosmology are the mentioned studies suggesting that spacetime quantization could effectively produce spacetime fuzziness/foam amenable to description in terms of a fluctuating spacetime metric [206, 557, 460] (see also Refs. [133, 525]). In particular one can consider [206] fluctuating spacetime metrics amounting to a fluctuating lightcone. Such fluctuations of the lightcone have implications for the arrival times of signals from distant sources that would result in a broadening of the spectra. It was observed in Ref. [206] that starting with a thermal spectrum one would end up with a slightly different spectrum. This can be summarized in a simple phenomenological formula for spectrum distorsion [206]

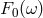where is the spectrum expected without the light-cone fluctuation effects and 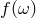encodes the corrections due to the lightcone fluctuations. Ref. [206] provides arguments in support of the possibility that the corrections due to lightcone fluctuations could get very large at large frequencies, with 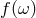growing like 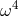. As we achieve better and better accuracy in the measurement of possible high-frequency departures from a thermal spectrum for the cosmic microwave background, we should then find evidence of such effects [206].

Ref. [460] also explored the possibility that lightcone fluctuations might have observable implications for the gravitational-wave background. The gravitational-wave background is always emitted much before the cosmic microwave background, but it was found [460] that the flat nature of the gravitational-wave-background spectrum is such that the effects of lightcone fluctuations are negligible.

6.3 Loop quantum cosmology

An area of quantum-spacetime cosmology that is not directly linked to the tools and scenarios considered in other areas of quantum-spacetime phenomenology is the Loop Quantum Cosmology (LQC) [125, 94, 126, 92] . This is a framework for implementing several effects seen to arise for the quantum spacetime of LQG in a cosmological setting. The most popular formulations of LQC are defined on “minisuperspace”, where one quantizes homogeneous spacetimes using the methods of LQG. And one finds that the characteristic discreteness of the LQG spacetime quantization change the dynamics of expanding Universe models. These changes are particularly significant at high densities, giving rise to mechanisms avoiding classical singularities.

And one can also consider the novel quantum-spacetime effects at later stages of the Universe expansion, when densities are lower and the corrections can be treated perturbatively in a gauge-invariant way. This can be done in particular for linear perturbations around spatially flat Friedmann–Robertson–Walker models, and the results are found to be primarily characterized in terms of “inverse-volume corrections”, due to the fact that the quantized densitized triad has a discrete spectrum, with the value zero contained in the spectrum. Essentially one finds that the LQG quantum-spacetime effects can be effectively described in terms of a novel repulsive force [92]. This repulsion can compete with the standard gravitational attraction, and can even become the dominant contribution, thereby evading the singularity, when the curvature is strong.

In Refs. [126, 92, 127], and references therein, readers can find a list of possible signatures of LQC. In my opinion, at present, such tests of predictions of LQC may tell us more about the choice of setup for incorporating the quantum-spacetime effects, rather than providing actual information on the quantum structure of spacetime. But as this novel approach keeps maturing, it may well turn into a key resource for experimentally probing the quantum structure of spacetime.

6.4 Cosmology with running spectral dimensions

As mentioned earlier in this review, several formalisms relevant to the study of the quantum-gravity problem have recently been shown to host the mechanism of running spectral dimensions. The spectral dimension of a spacetime is essentially defined [506] by considering a fictitious diffusion process, with the spectral dimension given in terms of the average return probability for given (fictitious) diffusion time. When the number of spectral dimensions matches the number of Hausdorff dimensions of a spacetime, the return probability depends on diffusion time in a characteristic way that is indeed found in all models for large diffusion times. But at short diffusion times one finds in several studies of interest for quantum-gravity and quantum-spacetime research that the average return probability has properties signaling a number of spectral dimensions smaller than the number of Hausdorff dimensions.

First results of this type were found in studies done within the framework of causal dynamical triangulations[48], naturally working with four Hausdorff dimensions and finding that the behavior at small diffusion times signaled two spectral dimensions. Two spectral dimensions for small diffusion times was then also found in studies inspired by asymptotic safety [360, 467] and studies based on Hořava–Liftschitz gravity [290]. A somewhat different situation is found in studies inspired by spacetime noncommutativity [110, 87, 31] and by spin foams [418], but still giving fewer than four spectral dimensions for small diffusion times (also see Refs. [506, 153]).

These “running spectral dimensions” could have very significant implications for cosmology, as suggested at least intuitively by the definition of spectral dimensions based on the dependence of the return probability on the diffusion time. At present these potentialities are still largely unexplored, but one possibility has been debated in Refs. [424, 505, 425]. Ref. [424], citing as motivation some of the quantum-gravity studies exhibiting running spectral dimensions, proposed that such studies should motivate the search for indirect evidence of the absence of gravitational degrees of freedom in the early Universe. However, Ref. [505] more prudently observed that gravitational degrees of freedom are indeed absent in spacetimes with three or fewer Hausdorff dimensions, but may well be present in spacetimes with four Hausdorff dimensions but with three or fewer spectral dimensions.

6.5 Some other quantum-gravity-cosmology proposals

So far in this section, consistent with the main goals of this review, I have focused on cosmology proposals that are based on (or at least directly linkable to) some theories of quantum spacetime. In this last part of the section, I mention just a few illustrative examples of ideas and proposals that are still based on the quantum-gravity problem, but without invoking any definite quantum properties of spacetime. It is not unlikely that future exploitations of the associated phenomenological opportunities would involve spacetime quantization.

6.5.1 Quantum-gravity-induced vector fields

An active area of quantum-gravity cosmology focuses on Lorentz-violating vector fields. These studies do not have as reference scenarios for spacetime quantization, but they are being linked generically to the opportunities that the quantum-gravity problem provides for the emergence of Lorentz-violating vector fields. Several possible implications are being considered, including the possibility that in the presence of such Lorentz-violating vector fields the Universe might experience a slower rate of expansion for a given matter content (see, e.g., Ref. [159]).

It is also emerging that the implications of such Lorentz-violating vector fields would be rather significant for the cosmic microwave background [368]. In particular, as stressed in other parts of this review, the presence of Lorentz-violating vector fields is often associated with energy-dependent birefringence. And the cosmic microwave background, since its radiation originates from the surface of last scattering, which is the most distant source of light, can be a very powerful opportunity to test anomalous features for the propagation of photons. Several techniques of data analysis have been developed that are capable of constraining the birefringence of photon propagation using cosmic-microwave-background data (see, e.g., Refs.[317, 315, 344, 270] and references therein).

6.5.2 A semiclassical Wheeler–DeWitt-based description of the early Universe

Cosmology is also an arena where some interest is attracted by studies of the semiclassical limit of quantum gravity. These do not invoke a quantum-spacetime picture and may not even rely on any given quantum-gravity proposal. They are rather viewed in analogy [325] with the semiclassical limits of other quantum theories: one can consider, for example, the corrections to the classical Maxwell action described by Heisenberg and Euler (in a pre-QED era) in terms of quantum fluctuations of electrons and positrons, which can now be rederived [325] from QED by integrating out the fermions and expanding in powers of .

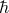These studies of the semiclassical limit of quantum gravity are often centered around the Wheeler–DeWitt equation. While for the development of a full quantum-gravity theory the Wheeler–DeWitt equation has proven to be extremely “cumbersome”, the fact that it is rather intuitively formulated is convenient for setting up a semiclassical approximation (see, e.g., Refs. [326, 447, 409]). A result that can be rather readily analyzed from a phenomenology perspective is the one providing [326] correction terms for the Schrödinger equation, obtained through a formal expansion of the Wheeler–DeWitt equation with respect to powers of the Planck mass. Unsurprisingly the relevant correction terms are far too small to matter in laboratory experiments [326]. However, it is plausible that such a procedure could give rise to observably large effects in the description of the early stages of the evolution of the Universe. In particular, the semiclassical approximation set up in Ref. [326] could be used rather straightforwardly to describe corrections to the Schrödinger equation for higher multipoles on a Friedman background.

6.5.3 No-singularity cosmology from string theory

An interesting string-theory-inspired area of cosmology research revolves around a scenario for singularity avoidance linked to the availability of duality tranformations, which allow one to set up a suitable “pre-Big-Bang” scenario [253, 143, 142]. In this scenario the Universe starts inflating from an initial state characterized by very small curvature and weak interactions. The small-curvature initial state is gravitationally unstable and would naturally evolve [253, 143, 142] into states with higher curvature, until string-size (roughly Planck-scale-size) effects are strong enough to induce a “bounce” into a decreasing-curvature regime. Instead of a conventional hot big bang one would have [253, 143, 142] a “hot big bounce” in which in particular the heating mechanism is provided by the quantum production of particles in the pre-bounce phase characterized by high curvature and strong interactions.

For this string-inspired pre-big-bang scenario several possible observational consequences have been discussed [253, 143, 142], including the one of a stochastic background of gravity waves due to a background of gravitons from the pre-big-bang phase. It appears to be plausible [253, 143, 142] that the magnitude of the associated effects might be within the range of sensitivities of modern gravity-wave interferometers.