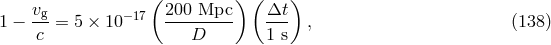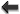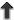7 Gravitational-Wave Tests of Gravitational Theory
7.1 Gravitational-wave observatories
Soon after the publication of this update, a new method of testing relativistic gravity will be realized, when
a worldwide network of upgraded laser interferometric gravitational-wave observatories in the U.S. (LIGO
Hanford and LIGO Livingston) and Europe (VIRGO and GEO600) begins regular detection and analysis of
gravitational-wave signals from astrophysical sources. Within a few years, they may be joined by an
underground cryogenic interferometer (KAGRA) in Japan, and around 2022, by a LIGO-type interferometer
in India. These broad-band antennas will have the capability of detecting and measuring the gravitational
waveforms from astronomical sources in a frequency band between about 10 Hz (the seismic
noise cutoff) and 500 Hz (the photon counting noise cutoff), with a maximum sensitivity to
strain at around 100 Hz of  (rms), for the kilometer-scale LIGO/VIRGO
projects. The most promising source for detection and study of the gravitational wave signal is
the “inspiralling compact binary” – a binary system of neutron stars or black holes (or one of
each) in the final minutes of a death spiral leading to a violent merger. Such is the fate, for
example, of the Hulse–Taylor binary pulsar B1913+16 in about 300 Myr, or the double pulsar
J0737–3039 in about 85 Myr. Given the expected sensitivity of the advanced LIGO-Virgo detectors,
which could see such sources out to many hundreds of megaparsecs, it has been estimated that
from 40 to several hundred annual inspiral events could be detectable. Other sources, such as
supernova core collapse events, instabilities in rapidly rotating newborn neutron stars, signals from
non-axisymmetric pulsars, and a stochastic background of waves, may be detectable (see [352] for a
review).
(rms), for the kilometer-scale LIGO/VIRGO
projects. The most promising source for detection and study of the gravitational wave signal is
the “inspiralling compact binary” – a binary system of neutron stars or black holes (or one of
each) in the final minutes of a death spiral leading to a violent merger. Such is the fate, for
example, of the Hulse–Taylor binary pulsar B1913+16 in about 300 Myr, or the double pulsar
J0737–3039 in about 85 Myr. Given the expected sensitivity of the advanced LIGO-Virgo detectors,
which could see such sources out to many hundreds of megaparsecs, it has been estimated that
from 40 to several hundred annual inspiral events could be detectable. Other sources, such as
supernova core collapse events, instabilities in rapidly rotating newborn neutron stars, signals from
non-axisymmetric pulsars, and a stochastic background of waves, may be detectable (see [352] for a
review).
In addition, plans are being developed for orbiting laser interferometer space antennae, such as DECIGO
in Japan and eLISA in Europe. The eLISA system would consist of three spacecraft orbiting the sun in a
triangular formation separated from each other by a million kilometers, and would be sensitive primarily in
the very low-frequency band between  and
and  , with peak strain sensitivity of order
, with peak strain sensitivity of order
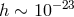 .
.
A third approach that focuses on the ultra low-frequency band (nanohertz) is that of Pulsar Timing Arrays (PTA), whereby a network of highly stable millisecond pulsars is monitored in a coherent way using radio telescopes, in hopes of detecting the fluctuations in arrival times induced by passing gravitational waves.
For recent reviews of the status of all these approaches to gravitational-wave detection, see the Proceedings of the 8th Edoardo Amaldi Conference on Gravitational Waves [272].
In addition to opening a new astronomical window, the detailed observation of gravitational waves by such observatories may provide the means to test general relativistic predictions for the polarization and speed of the waves, for gravitational radiation damping and for strong-field gravity. These topics have been thoroughly covered in two recent Living Reviews by Gair et al. [170] for space-based detectors, and by Yunes and Siemens [452] for ground-based detectors. Here we present a brief overview.
7.2 Gravitational-wave amplitude and polarization
7.2.1 General relativity
A generic gravitational wave detector can be modelled as a body of mass 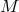 at a distance
at a distance 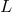 from a
fiducial laboratory point, connected to the point by a spring of resonant frequency
from a
fiducial laboratory point, connected to the point by a spring of resonant frequency 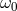 and quality
factor
and quality
factor 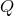 . From the equation of geodesic deviation, the infinitesimal displacement
. From the equation of geodesic deviation, the infinitesimal displacement 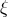 of the
mass along the line of separation from its equilibrium position satisfies the equation of motion
of the
mass along the line of separation from its equilibrium position satisfies the equation of motion
 and
and 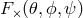 are “beam-pattern” factors that depend on the direction of the
source
are “beam-pattern” factors that depend on the direction of the
source 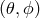 and on a polarization angle
and on a polarization angle  , and
, and 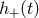 and
and 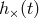 are gravitational
waveforms corresponding to the two polarizations of the gravitational wave (for pedagogical
reviews, see [386, 324*]). In a source coordinate system in which the
are gravitational
waveforms corresponding to the two polarizations of the gravitational wave (for pedagogical
reviews, see [386, 324*]). In a source coordinate system in which the  plane is the plane
of the sky and the
plane is the plane
of the sky and the  -direction points toward the detector, these two modes are given by
where
-direction points toward the detector, these two modes are given by
where 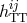 represent transverse-traceless (TT) projections of the calculated waveform of Eq. (84*), given
by
where
represent transverse-traceless (TT) projections of the calculated waveform of Eq. (84*), given
by
where 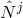 is a unit vector pointing toward the detector. The beam pattern factors depend
on the orientation and nature of the detector. For a wave approaching along the laboratory
is a unit vector pointing toward the detector. The beam pattern factors depend
on the orientation and nature of the detector. For a wave approaching along the laboratory
 -direction, and for a mass whose location on the
-direction, and for a mass whose location on the  plane makes an angle
plane makes an angle 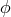 with the
with the
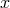 -axis, the beam pattern factors are given by
-axis, the beam pattern factors are given by 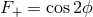 and
and 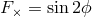 . For a laser
interferometer with one arm along the laboratory
. For a laser
interferometer with one arm along the laboratory  -axis, the other along the
-axis, the other along the  -axis, with
-axis, with  defined as the differential displacement along the two arms, the beam pattern functions are
Here, we assume that
defined as the differential displacement along the two arms, the beam pattern functions are
Here, we assume that 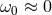 in Eq. (124*), corresponding to the essentially free motion of the suspended
mirrors in the horizontal direction. For a laser interferometer in which the angle between the arms is
in Eq. (124*), corresponding to the essentially free motion of the suspended
mirrors in the horizontal direction. For a laser interferometer in which the angle between the arms is 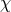 ,
the overall response is reduced by
,
the overall response is reduced by 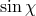 ; for a space-based interferometer such as eLISA,
; for a space-based interferometer such as eLISA,
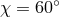 .
.
The waveforms 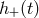 and
and 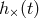 depend on the nature and evolution of the source. For example, for
a binary system in a circular orbit, with an inclination
depend on the nature and evolution of the source. For example, for
a binary system in a circular orbit, with an inclination 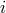 relative to the plane of the sky, and the
relative to the plane of the sky, and the 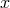 -axis
oriented along the major axis of the projected orbit, the quadrupole approximation of Eq. (86*) gives
-axis
oriented along the major axis of the projected orbit, the quadrupole approximation of Eq. (86*) gives
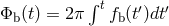 is the orbital phase.
is the orbital phase.
7.2.2 Alternative theories of gravity
A generic gravitational wave detector whose scale is small compared to the gravitational wavelength
measures the local components of a symmetric 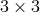 tensor which is composed of the “electric”
components of the Riemann curvature tensor,
tensor which is composed of the “electric”
components of the Riemann curvature tensor, 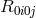 , via the equation of geodesic deviation, given, for a
pair of freely falling particles by
, via the equation of geodesic deviation, given, for a
pair of freely falling particles by 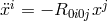 , where
, where 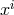 denotes the spatial separation. In general
there are six independent components, which can be expressed in terms of polarizations (modes with
specific transformation properties under rotations and boosts); for a wave propagating in the
denotes the spatial separation. In general
there are six independent components, which can be expressed in terms of polarizations (modes with
specific transformation properties under rotations and boosts); for a wave propagating in the  -direction,
they can be displayed by the matrix
-direction,
they can be displayed by the matrix
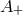 ,
, 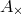 , and
, and 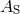 ) are transverse to the direction of propagation, with two representing
quadrupolar deformations and one representing a monopolar transverse “breathing” deformation.
Three modes are longitudinal, with one (
) are transverse to the direction of propagation, with two representing
quadrupolar deformations and one representing a monopolar transverse “breathing” deformation.
Three modes are longitudinal, with one (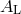 ) an axially symmetric stretching mode in the
propagation direction, and one quadrupolar mode in each of the two orthogonal planes containing the
propagation direction (
) an axially symmetric stretching mode in the
propagation direction, and one quadrupolar mode in each of the two orthogonal planes containing the
propagation direction (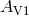 and
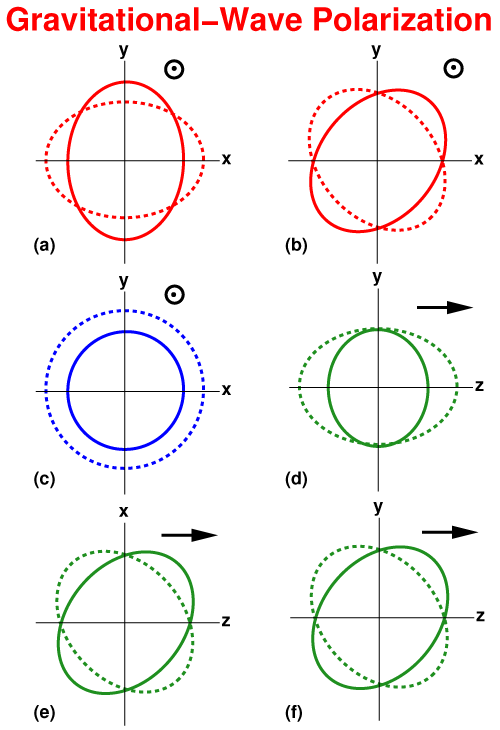
and 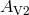 ). Figure 10* shows the displacements induced on a ring of
freely falling test particles by each of these modes. General relativity predicts only the first two
transverse quadrupolar modes (a) and (b) independently of the source; these correspond to the
waveforms
). Figure 10* shows the displacements induced on a ring of
freely falling test particles by each of these modes. General relativity predicts only the first two
transverse quadrupolar modes (a) and (b) independently of the source; these correspond to the
waveforms 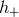 and
and 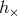 discussed earlier (note the
discussed earlier (note the 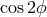 and
and 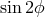 dependences of the
displacements).
dependences of the
displacements).
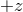 direction. There is no displacement out of the plane of the picture. In (a),
(b), and (c), the wave propagates out of the plane; in (d), (e), and (f), the wave propagates in the
plane. In GR, only (a) and (b) are present; in massless scalar–tensor gravity, (c) may also be present.
direction. There is no displacement out of the plane of the picture. In (a),
(b), and (c), the wave propagates out of the plane; in (d), (e), and (f), the wave propagates in the
plane. In GR, only (a) and (b) are present; in massless scalar–tensor gravity, (c) may also be present. Massless scalar–tensor gravitational waves can in addition contain the transverse breathing mode (c).
This can be obtained from the physical waveform  , which is related to
, which is related to 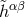 and
and  to the required
order by
to the required
order by
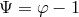 . In this case,
. In this case, 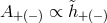 , while
, while 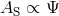 (see Eqs. (99*), (100*), (101*) and (102*)
for the leading contributions to these fields). In massive scalar–tensor theories, the longitudinal
mode (d) can also be present, but is suppressed relative to (c) by a factor
(see Eqs. (99*), (100*), (101*) and (102*)
for the leading contributions to these fields). In massive scalar–tensor theories, the longitudinal
mode (d) can also be present, but is suppressed relative to (c) by a factor  , where
, where
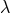 is the wavelength of the radiation, and
is the wavelength of the radiation, and 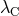 is the Compton wavelength of the massive
scalar.
is the Compton wavelength of the massive
scalar.
More general metric theories predict additional longitudinal modes, up to the full complement of six (TEGP 10.2 [420*]). For example, Einstein-Æther theory generically predicts all six modes [205].
A suitable array of gravitational antennas could delineate or limit the number of modes present
in a given wave. The strategy depends on whether or not the source direction is known. In
general there are eight unknowns (six polarizations and two direction cosines), but only six
measurables (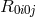 ). If the direction can be established by either association of the waves with
optical or other observations, or by time-of-flight measurements between separated detectors,
then six suitably oriented detectors suffice to determine all six components. If the direction
cannot be established, then the system is underdetermined, and no unique solution can be
found. However, if one assumes that only transverse waves are present, then there are only three
unknowns if the source direction is known, or five unknowns otherwise. Then the corresponding
number (three or five) of detectors can determine the polarization. If distinct evidence were found
of any mode other than the two transverse quadrupolar modes of GR, the result would be
disastrous for GR. On the other hand, the absence of a breathing mode would not necessarily
rule out scalar–tensor gravity, because the strength of that mode depends on the nature of the
source.
). If the direction can be established by either association of the waves with
optical or other observations, or by time-of-flight measurements between separated detectors,
then six suitably oriented detectors suffice to determine all six components. If the direction
cannot be established, then the system is underdetermined, and no unique solution can be
found. However, if one assumes that only transverse waves are present, then there are only three
unknowns if the source direction is known, or five unknowns otherwise. Then the corresponding
number (three or five) of detectors can determine the polarization. If distinct evidence were found
of any mode other than the two transverse quadrupolar modes of GR, the result would be
disastrous for GR. On the other hand, the absence of a breathing mode would not necessarily
rule out scalar–tensor gravity, because the strength of that mode depends on the nature of the
source.
For laser interferometers, the signal controlling the laser phase output can be written in the form
where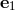 and
and  are unit vectors directed along the two arms of the interferometer. The final result is
where the angular pattern functions
are unit vectors directed along the two arms of the interferometer. The final result is
where the angular pattern functions 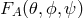 are given by
(see [324] for detailed derivations and definitions). Note that the scalar and longitudinal pattern
functions are degenerate and thus no array of laser interferometers can measure these two modes
separately.
are given by
(see [324] for detailed derivations and definitions). Note that the scalar and longitudinal pattern
functions are degenerate and thus no array of laser interferometers can measure these two modes
separately.
Some of the details of implementing such polarization observations have been worked out for arrays of
resonant cylindrical, disk-shaped, spherical, and truncated icosahedral detectors (TEGP 10.2 [420*], for
recent reviews see [256, 403]). Early work to assess whether the ground-based or space-based
laser interferometers (or combinations of the two types) could perform interesting polarization
measurements was carried out in [404, 70, 267, 171, 411]; for a recent detailed analysis see [301].
Unfortunately for this purpose, the two LIGO observatories (in Washington and Louisiana
states, respectively) have been constructed to have their respective arms as parallel as possible,
apart from the curvature of the Earth; while this maximizes the joint sensitivity of the two
detectors to gravitational waves, it minimizes their ability to detect two modes of polarization.
In this regard the addition of Virgo, and the future KAGRA and LIGO-India systems will
be crucial to polarization measurements. By combining signals from various interferometers
into a kind of “null channel” one can test for the existence of modes beyond the 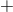 and
and  modes in a model independent manner [78]. The capability of space-based interferometers to
measure the polarization modes was assessed in detail in [388, 302]. For pulsar timing arrays,
see [245, 14, 74].
modes in a model independent manner [78]. The capability of space-based interferometers to
measure the polarization modes was assessed in detail in [388, 302]. For pulsar timing arrays,
see [245, 14, 74].
7.3 Gravitational-wave phase evolution
7.3.1 General relativity
In the binary pulsar, a test of GR was made possible by measuring at least three relativistic effects that
depended upon only two unknown masses. The evolution of the orbital phase under the damping effect of
gravitational radiation played a crucial role. Another situation in which measurement of orbital phase can
lead to tests of GR is that of the inspiralling compact binary system. The key differences are that here
gravitational radiation itself is the detected signal, rather than radio pulses, and the phase
evolution alone carries all the information. In the binary pulsar, the first derivative of the binary
frequency 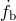 was measured; here the full nonlinear variation of
was measured; here the full nonlinear variation of 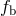 as a function of time is
measured.
as a function of time is
measured.
Broad-band laser interferometers are especially sensitive to the phase evolution of the gravitational
waves, which carry the information about the orbital phase evolution. The analysis of gravitational wave
data from such sources will involve some form of matched filtering of the noisy detector output against an
ensemble of theoretical “template” waveforms which depend on the intrinsic parameters of the inspiralling
binary, such as the component masses, spins, and so on, and on its inspiral evolution. How accurate must a
template be in order to “match” the waveform from a given source (where by a match we mean maximizing
the cross-correlation or the signal-to-noise ratio)? In the total accumulated phase of the wave detected in
the sensitive bandwidth, the template must match the signal to a fraction of a cycle. For two
inspiralling neutron stars detected by the advanced LIGO/Virgo systems, around 16 000 cycles
should be detected during the final few minutes of inspiral; this implies a phasing accuracy of
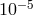 or better. Since
or better. Since 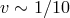 during the late inspiral, this means that correction terms
in the phasing at the level of
during the late inspiral, this means that correction terms
in the phasing at the level of 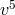 or higher are needed. More formal analyses confirm this
intuition [99, 153, 97, 323].
or higher are needed. More formal analyses confirm this
intuition [99, 153, 97, 323].
Because it is a slow-motion system ( ), the binary pulsar is sensitive only to the lowest-order
effects of gravitational radiation as predicted by the quadrupole formula. Nevertheless, the first correction
terms of order
), the binary pulsar is sensitive only to the lowest-order
effects of gravitational radiation as predicted by the quadrupole formula. Nevertheless, the first correction
terms of order  and
and  to the quadrupole formula were calculated as early as 1976 [405] (see
TEGP 10.3 [420*]).
to the quadrupole formula were calculated as early as 1976 [405] (see
TEGP 10.3 [420*]).
But for laser interferometric observations of gravitational waves, the bottom line is that, in order to measure the astrophysical parameters of the source and to test the properties of the gravitational waves, it is necessary to derive the gravitational waveform and the resulting radiation back-reaction on the orbit phasing at least to 3PN order beyond the quadrupole approximation.
For the special case of non-spinning bodies moving on quasi-circular orbits (i.e., circular apart from a
slow inspiral), the evolution of the gravitational wave frequency 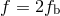 through 2PN order has the form
through 2PN order has the form
 . The first term is the quadrupole contribution (compare Eq. (88*)), the second term
is the 1PN contribution, the third term, with the coefficient
. The first term is the quadrupole contribution (compare Eq. (88*)), the second term
is the 1PN contribution, the third term, with the coefficient 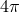 , is the “tail” contribution,
and the fourth term is the 2PN contribution. Two decades of intensive work by many groups
have led to the development of waveforms in GR that are accurate to 3.5PN order, and for
some specific effects, such as those related to spin, to 4.5PN order (see [51] for a thorough
review).
, is the “tail” contribution,
and the fourth term is the 2PN contribution. Two decades of intensive work by many groups
have led to the development of waveforms in GR that are accurate to 3.5PN order, and for
some specific effects, such as those related to spin, to 4.5PN order (see [51] for a thorough
review).
Similar expressions can be derived for the loss of angular momentum and linear momentum. Expressions
for non-circular orbits have also been derived [175, 107]. These losses react back on the orbit to circularize
it and cause it to inspiral. The result is that the orbital phase (and consequently the gravitational wave
phase) evolves non-linearly with time. It is the sensitivity of the broad-band laser interferometric
detectors to phase that makes the higher-order contributions to 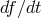 so observationally
relevant.
so observationally
relevant.
If the coefficients of each of the powers of 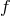 in Eq. (135*) can be measured, then one again obtains
more than two constraints on the two unknowns
in Eq. (135*) can be measured, then one again obtains
more than two constraints on the two unknowns 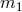 and
and 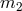 , leading to the possibility to test GR. For
example, Blanchet and Sathyaprakash [59, 60] have shown that, by observing a source with a sufficiently
strong signal, an interesting test of the
, leading to the possibility to test GR. For
example, Blanchet and Sathyaprakash [59, 60] have shown that, by observing a source with a sufficiently
strong signal, an interesting test of the 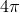 coefficient of the “tail” term could be performed (but see [22]
for a more sophisticated analysis).
coefficient of the “tail” term could be performed (but see [22]
for a more sophisticated analysis).
Another possibility involves gravitational waves from a small mass orbiting and inspiralling into a (possibly supermassive) spinning black hole. A general non-circular, non-equatorial orbit will precess around the hole, both in periastron and in orbital plane, leading to a complex gravitational waveform that carries information about the non-spherical, strong-field spacetime around the hole. According to GR, this spacetime must be the Kerr spacetime of a rotating black hole, uniquely specified by its mass and angular momentum, and consequently, observation of the waves could test this fundamental hypothesis of GR [345, 322].
7.3.2 Alternative theories of gravity
In general, alternative theories of gravity will predict rather different phase evolution from that of GR, notably via the addition of dipole gravitational radiation. For example, the dipole gravitational radiation predicted by scalar–tensor theories modifies the gravitational radiation back-reaction, and thereby the phase evolution. Including only the leading 0PN and –1PN (dipole) contributions, one obtains,
where , and
, and 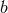 is the coefficient of the dipole term, given to first order in
is the coefficient of the dipole term, given to first order in 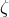 by
by
 , where
, where  is given by Eq. (104*),
is given by Eq. (104*), 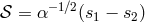 and
and 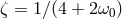 .
Double neutron star systems are not promising because the small range of masses available near
.
Double neutron star systems are not promising because the small range of masses available near 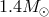 results in suppression of dipole radiation by symmetry. For black holes,
results in suppression of dipole radiation by symmetry. For black holes,  identically, consequently
double black hole systems turn out to be observationally identical in the two theories. Thus mixed systems
involving a neutron star and a black hole are preferred. However, a number of analyses of the capabilities of
both ground-based and space-based (eLISA) observatories have shown that observing waves
from neutron-star–black-hole inspirals is not likely to bound scalar–tensor gravity at a level
competitive with the Cassini bound, with future solar-system improvements, or with binary pulsar
observations [422, 236, 106, 353, 433*, 41*, 42*, 445]. A possible exception is DECIGO/BBO, a
proposed space gravitational-wave observatory with peak sensitivity between the eLISA and
LIGO/Virgo bands; observations of inspirals of neutron stars onto hypothetical intermediate
mass (
identically, consequently
double black hole systems turn out to be observationally identical in the two theories. Thus mixed systems
involving a neutron star and a black hole are preferred. However, a number of analyses of the capabilities of
both ground-based and space-based (eLISA) observatories have shown that observing waves
from neutron-star–black-hole inspirals is not likely to bound scalar–tensor gravity at a level
competitive with the Cassini bound, with future solar-system improvements, or with binary pulsar
observations [422, 236, 106, 353, 433*, 41*, 42*, 445]. A possible exception is DECIGO/BBO, a
proposed space gravitational-wave observatory with peak sensitivity between the eLISA and
LIGO/Virgo bands; observations of inspirals of neutron stars onto hypothetical intermediate
mass (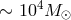 ) black holes could improve upon the Cassini bound by several orders of
magnitude [446].
) black holes could improve upon the Cassini bound by several orders of
magnitude [446].
These considerations suggest that it might be fruitful to attempt to parametrize the phasing formulae in a manner reminiscent of the PPN framework for post-Newtonian gravity. A number of approaches along this line have been developed, including the parametrized post-Einsteinian (PPE) framework [451, 347], a Bayesian parametrized approach [250], and a parametrization based on the post-Newtonian expansions discussed above [288]. The discovery of relationships between the moment of inertia, the gravitational Love number, and the quadrupole moment of neutron stars (“I-Love-Q” relations) in general relativity has opened the possibility of testing theories using gravitational waves in a manner that is relatively free of contamination from the neutron-star equation of state [448, 447].
7.4 Speed of gravitational waves
According to GR, in the limit in which the wavelength of gravitational waves is small compared to the
radius of curvature of the background spacetime, the waves propagate along null geodesics of the
background spacetime, i.e., they have the same speed  as light (in this section, we do not set
as light (in this section, we do not set 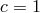 ). In
other theories, the speed could differ from
). In
other theories, the speed could differ from  because of coupling of gravitation to “background”
gravitational fields. For example, in the Rosen bimetric theory with a flat background metric
because of coupling of gravitation to “background”
gravitational fields. For example, in the Rosen bimetric theory with a flat background metric
 , gravitational waves follow null geodesics of
, gravitational waves follow null geodesics of 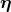 , while light follows null geodesics of
, while light follows null geodesics of 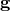 (TEGP 10.1 [420*]).
(TEGP 10.1 [420*]).
Another way in which the speed of gravitational waves could differ from  is if gravitation were
propagated by a massive field (a massive graviton), in which case
is if gravitation were
propagated by a massive field (a massive graviton), in which case 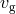 would be given by, in a local inertial
frame,
would be given by, in a local inertial
frame,
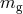 and
and 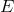 are the graviton rest mass and energy, respectively.
are the graviton rest mass and energy, respectively.
The most obvious way to test this is to compare the arrival times of a gravitational wave and an
electromagnetic wave from the same event, e.g., a supernova or a prompt gamma-ray burst. For a source at
a distance 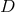 , the resulting value of the difference
, the resulting value of the difference 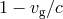 is
is
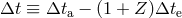 is the “time difference”, where
is the “time difference”, where 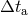 and
and 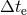 are the differences in
arrival time and emission time of the two signals, respectively, and
are the differences in
arrival time and emission time of the two signals, respectively, and 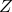 is the redshift of the source. In
many cases,
is the redshift of the source. In
many cases, 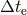 is unknown, so that the best one can do is employ an upper bound on
is unknown, so that the best one can do is employ an upper bound on  based on
observation or modelling. The result will then be a bound on
based on
observation or modelling. The result will then be a bound on 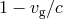 .
.
For a massive graviton, if the frequency of the gravitational waves is such that 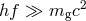 , where
, where
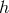 is Planck’s constant, then
is Planck’s constant, then 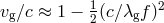 , where
, where 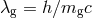 is the graviton
Compton wavelength, and the bound on
is the graviton
Compton wavelength, and the bound on 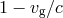 can be converted to a bound on
can be converted to a bound on 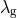 , given by
, given by
The foregoing discussion assumes that the source emits both gravitational and electromagnetic radiation in detectable amounts, and that the relative time of emission can be established to sufficient accuracy, or can be shown to be sufficiently small.
However, there is a situation in which a bound on the graviton mass can be set using gravitational
radiation alone [423*]. That is the case of the inspiralling compact binary. Because the frequency of
the gravitational radiation sweeps from low frequency at the initial moment of observation
to higher frequency at the final moment, the speed of the gravitons emitted will vary, from
lower speeds initially to higher speeds (closer to  ) at the end. This will cause a distortion of
the observed phasing of the waves and result in a shorter than expected overall time
) at the end. This will cause a distortion of
the observed phasing of the waves and result in a shorter than expected overall time 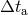 of
passage of a given number of cycles. Furthermore, through the technique of matched filtering, the
parameters of the compact binary can be measured accurately (assuming that GR is a good
approximation to the orbital evolution, even in the presence of a massive graviton), and thereby the
emission time
of
passage of a given number of cycles. Furthermore, through the technique of matched filtering, the
parameters of the compact binary can be measured accurately (assuming that GR is a good
approximation to the orbital evolution, even in the presence of a massive graviton), and thereby the
emission time 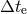 can be determined accurately. Roughly speaking, the “phase interval”
can be determined accurately. Roughly speaking, the “phase interval”
 in Eq. (139*) can be measured to an accuracy
in Eq. (139*) can be measured to an accuracy 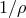 , where
, where 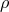 is the signal-to-noise
ratio.
is the signal-to-noise
ratio.
Thus one can estimate the bounds on 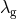 achievable for various compact inspiral systems, and for
various detectors. For stellar-mass inspiral (neutron stars or black holes) observed by the LIGO/VIRGO
class of ground-based interferometers,
achievable for various compact inspiral systems, and for
various detectors. For stellar-mass inspiral (neutron stars or black holes) observed by the LIGO/VIRGO
class of ground-based interferometers,  ,
, 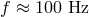 , and
, and 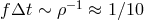 . The result
is
. The result
is 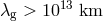 . For supermassive binary black holes (
. For supermassive binary black holes (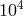 to
to  ) observed by the proposed laser
interferometer space antenna (LISA),
) observed by the proposed laser
interferometer space antenna (LISA), 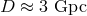 ,
, 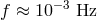 , and
, and 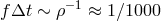 . The result
is
. The result
is 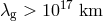 .
.
A full noise analysis using proposed noise curves for the advanced LIGO and for LISA weakens these
crude bounds by factors between two and 10 [423, 433, 41*, 42, 23, 377, 445]. For example, for the inspiral
of two 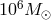 black holes with aligned spins at a distance of
black holes with aligned spins at a distance of 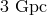 observed by LISA, a bound of
observed by LISA, a bound of
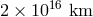 could be placed [41]. Other possibilities include using binary pulsar data to bound
modifications of gravitational radiation damping by a massive graviton [154], using LISA observations of
the phasing of waves from compact white-dwarf binaries, eccentric galactic binaries, and eccentric inspiral
binaries [98, 209], using pulsar timing arrays [244], and using DECIGO/BBO to observe neutron-star
intermediate-mass black-hole inspirals [446].
could be placed [41]. Other possibilities include using binary pulsar data to bound
modifications of gravitational radiation damping by a massive graviton [154], using LISA observations of
the phasing of waves from compact white-dwarf binaries, eccentric galactic binaries, and eccentric inspiral
binaries [98, 209], using pulsar timing arrays [244], and using DECIGO/BBO to observe neutron-star
intermediate-mass black-hole inspirals [446].
Bounds obtainable from gravitational radiation effects should be compared with the solid bound
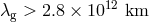 [381] derived from solar system dynamics, which limit the presence of a Yukawa
modification of Newtonian gravity of the form
[381] derived from solar system dynamics, which limit the presence of a Yukawa
modification of Newtonian gravity of the form
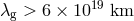 from consideration of galactic and cluster
dynamics [401].
from consideration of galactic and cluster
dynamics [401].
Mirshekari et al. [287] studied bounds that could be placed on more general graviton dispersion relations that could emerge from alternative theories with Lorentz violation, in which the effective propagation speed is given by
where and
and 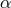 are parameters that depend on the theory.
are parameters that depend on the theory.

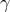
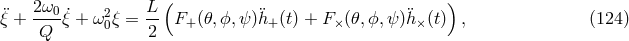
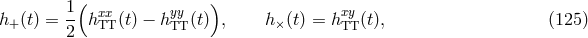
![[( )( ) ( ) ( )] hij = hkl δik − Nˆi ˆN k δjl − NˆjNˆl − 1- δij − NˆiNˆj δkl − NˆkNˆl , (126 ) TT 2](article1442x.gif)
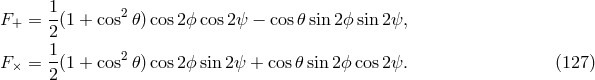
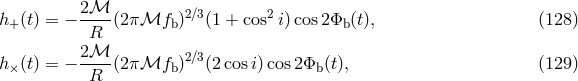


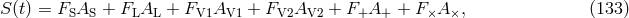

![[ ( ) 96π 2 5∕3 743 11 2∕3 ˙f = -5--f (πℳf ) 1 − 336-+ 4-η (πmf ) + 4π (πmf ) ( ) ] 34103- 13661- 59- 2 4∕3 5∕3 + 18144 + 2016 η + 18 η (πmf ) + 𝒪[(πmf ) ] , (135 )](article1510x.gif)
![f˙= 96π-f2(πα ℳf )5∕3κ1-[1 + b(πmf )− 2∕3] , (136 ) 5 12](article1518x.gif)