6 Stellar System Tests of Gravitational Theory
6.1 The binary pulsar and general relativity
The 1974 discovery of the binary pulsar B1913+16 by Joseph Taylor and Russell Hulse during a routine search for new pulsars provided the first possibility of probing new aspects of gravitational theory: the effects of strong relativistic internal gravitational fields on orbital dynamics, and the effects of gravitational radiation reaction. For reviews of the discovery, see the published Nobel Prize lectures by Hulse and Taylor [195, 385]. For reviews of the current status of testing general relativity with pulsars, including binary and millisecond pulsars, see [261, 374, 412]; specific details on every pulsar discovered to date, along with orbit elements of pulsars in binary systems, can be found at the Australia Telescope National Facility (ATNF) online pulsar catalogue [28]. Table 7 lists the current values of the key orbital and relativistic parameters for B1913+16, from analysis of data through 2006 [409].
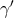 is not the same as the PPN parameter
is not the same as the PPN parameter 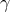 [see
Eqs. (108*)].
[see
Eqs. (108*)].| Parameter |
Symbol
|
Value
|
|
(units)
|
||
| (i) Astrometric and spin parameters: | ||
| Right Ascension |  |
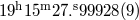 |
| Declination |  |
 |
| Pulsar period | 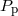 (ms) (ms) |
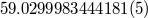 |
| Derivative of period | 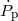 |
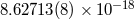 |
| (ii) “Keplerian” parameters: | ||
| Projected semimajor axis | 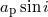 (s) (s) |
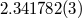 |
| Eccentricity |  |
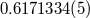 |
| Orbital period | 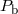 (day) (day) |
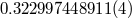 |
| Longitude of periastron | 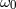 ( ( ) ) |
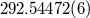 |
| Julian date of periastron | 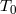 (MJD) (MJD) |
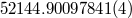 |
| (iii) “Post-Keplerian” parameters: | ||
| Mean rate of periastron advance | 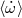 ( ( ) ) |
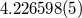 |
| Redshift/time dilation |  (ms) (ms) |
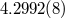 |
| Orbital period derivative |  ( ( ) ) |
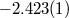 |
The system consists of a pulsar of nominal period 59 ms in a close binary orbit with an unseen
companion. The orbital period is about 7.75 hours, and the eccentricity is 0.617. From detailed analyses of
the arrival times of pulses (which amounts to an integrated version of the Doppler-shift methods used in
spectroscopic binary systems), extremely accurate orbital and physical parameters for the system have
been obtained (see Table 7). Because the orbit is so close (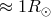 ) and because there is
no evidence of an eclipse of the pulsar signal or of mass transfer from the companion, it is
generally agreed that the companion is compact. Evolutionary arguments suggest that it is
most likely a dead pulsar, while B1913+16 is a “recycled” pulsar. Thus the orbital motion
is very clean, free from tidal or other complicating effects. Furthermore, the data acquisition
is “clean” in the sense that by exploiting the intrinsic stability of the pulsar clock combined
with the ability to maintain and transfer atomic time accurately using GPS, the observers can
keep track of pulse time-of-arrival with an accuracy of
) and because there is
no evidence of an eclipse of the pulsar signal or of mass transfer from the companion, it is
generally agreed that the companion is compact. Evolutionary arguments suggest that it is
most likely a dead pulsar, while B1913+16 is a “recycled” pulsar. Thus the orbital motion
is very clean, free from tidal or other complicating effects. Furthermore, the data acquisition
is “clean” in the sense that by exploiting the intrinsic stability of the pulsar clock combined
with the ability to maintain and transfer atomic time accurately using GPS, the observers can
keep track of pulse time-of-arrival with an accuracy of 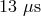 , despite extended gaps between
observing sessions (including a several-year gap in the middle 1990s for an upgrade of the Arecibo
radio telescope). The pulsar has experienced only one small “glitch” in its pulse period, in May
2003.
, despite extended gaps between
observing sessions (including a several-year gap in the middle 1990s for an upgrade of the Arecibo
radio telescope). The pulsar has experienced only one small “glitch” in its pulse period, in May
2003.
Three factors made this system an arena where relativistic celestial mechanics must be used: the
relatively large size of relativistic effects [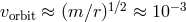 ], a factor of 10 larger than the
corresponding values for solar-system orbits; the short orbital period, allowing secular effects to build up
rapidly; and the cleanliness of the system, allowing accurate determinations of small effects. Because the
orbital separation is large compared to the neutron stars’ compact size, tidal effects can be ignored.
Just as Newtonian gravity is used as a tool for measuring astrophysical parameters of ordinary
binary systems, so GR is used as a tool for measuring astrophysical parameters in the binary
pulsar.
], a factor of 10 larger than the
corresponding values for solar-system orbits; the short orbital period, allowing secular effects to build up
rapidly; and the cleanliness of the system, allowing accurate determinations of small effects. Because the
orbital separation is large compared to the neutron stars’ compact size, tidal effects can be ignored.
Just as Newtonian gravity is used as a tool for measuring astrophysical parameters of ordinary
binary systems, so GR is used as a tool for measuring astrophysical parameters in the binary
pulsar.
The observational parameters that are obtained from a least-squares solution of the arrival-time data fall into three groups:
- non-orbital parameters, such as the pulsar period and its rate of change (defined at a given epoch), and the position of the pulsar on the sky;
- five “Keplerian” parameters, most closely related to those appropriate for standard Newtonian
binary systems, such as the eccentricity
 , the orbital period
, the orbital period 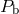 , and the semi-major axis
of the pulsar projected along the line of sight,
, and the semi-major axis
of the pulsar projected along the line of sight,  ; and
; and
- five “post-Keplerian” parameters.
The five post-Keplerian parameters are: 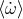 , the average rate of periastron advance;
, the average rate of periastron advance; 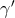 , the amplitude of
delays in arrival of pulses caused by the varying effects of the gravitational redshift and time dilation as the
pulsar moves in its elliptical orbit at varying distances from the companion and with varying speeds;
, the amplitude of
delays in arrival of pulses caused by the varying effects of the gravitational redshift and time dilation as the
pulsar moves in its elliptical orbit at varying distances from the companion and with varying speeds; 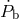 ,
the rate of change of orbital period, caused predominantly by gravitational radiation damping; and
,
the rate of change of orbital period, caused predominantly by gravitational radiation damping; and  and
and
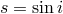 , respectively the “range” and “shape” of the Shapiro time delay of the pulsar signal as it
propagates through the curved spacetime region near the companion, where
, respectively the “range” and “shape” of the Shapiro time delay of the pulsar signal as it
propagates through the curved spacetime region near the companion, where 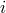 is the angle of inclination of
the orbit relative to the plane of the sky. An additional 14 relativistic parameters are measurable in
principle [119].
is the angle of inclination of
the orbit relative to the plane of the sky. An additional 14 relativistic parameters are measurable in
principle [119].
In GR, the five post-Keplerian parameters can be related to the masses of the two bodies and to measured Keplerian parameters by the equations (TEGP 12.1, 14.6 (a) [420*])
where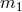 and
and 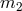 denote the pulsar and companion masses, respectively. The formula
for
denote the pulsar and companion masses, respectively. The formula
for 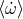 ignores possible non-relativistic contributions to the periastron shift, such as tidally
or rotationally induced effects caused by the companion (for discussion of these effects, see
TEGP 12.1 (c) [420*]). The formula for
ignores possible non-relativistic contributions to the periastron shift, such as tidally
or rotationally induced effects caused by the companion (for discussion of these effects, see
TEGP 12.1 (c) [420*]). The formula for 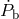 includes only quadrupole gravitational radiation; it ignores
other sources of energy loss, such as tidal dissipation (TEGP 12.1 (f) [420*]). Notice that, by virtue of
Kepler’s third law,
includes only quadrupole gravitational radiation; it ignores
other sources of energy loss, such as tidal dissipation (TEGP 12.1 (f) [420*]). Notice that, by virtue of
Kepler’s third law, 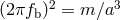 ,
, 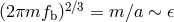 , thus the first two post-Keplerian
parameters can be seen as
, thus the first two post-Keplerian
parameters can be seen as 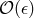 , or 1PN corrections to the underlying variable, while the
third is an
, or 1PN corrections to the underlying variable, while the
third is an 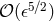 , or 2.5PN correction. The current observed values for the Keplerian and
post-Keplerian parameters are shown in Table 7. The parameters
, or 2.5PN correction. The current observed values for the Keplerian and
post-Keplerian parameters are shown in Table 7. The parameters  and
and  are not separately
measurable with interesting accuracy for B1913+16 because the orbit’s
are not separately
measurable with interesting accuracy for B1913+16 because the orbit’s  inclination does not
lead to a substantial Shapiro delay. However they are measurable in the double pulsar, for
example.
inclination does not
lead to a substantial Shapiro delay. However they are measurable in the double pulsar, for
example.
Because  and
and  are separately measured parameters, the measurement of the three post-Keplerian
parameters provides three constraints on the two unknown masses. The periastron shift measures the total
mass of the system,
are separately measured parameters, the measurement of the three post-Keplerian
parameters provides three constraints on the two unknown masses. The periastron shift measures the total
mass of the system,  measures the chirp mass, and
measures the chirp mass, and 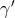 measures a complicated function of the masses.
GR passes the test if it provides a consistent solution to these constraints, within the measurement
errors.
measures a complicated function of the masses.
GR passes the test if it provides a consistent solution to these constraints, within the measurement
errors.
From the intersection of the  and
and  constraints we obtain the values
constraints we obtain the values  and
and
 . The third of Eqs. (108*) then predicts the value
. The third of Eqs. (108*) then predicts the value 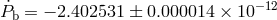 .
In order to compare the predicted value for
.
In order to compare the predicted value for 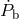 with the observed value of Table 7, it is necessary to take
into account the small kinematic effect of a relative acceleration between the binary pulsar system and the
solar system caused by the differential rotation of the galaxy. Using data on the location and proper motion
of the pulsar, combined with the best information available on galactic rotation; the current value of this
effect is
with the observed value of Table 7, it is necessary to take
into account the small kinematic effect of a relative acceleration between the binary pulsar system and the
solar system caused by the differential rotation of the galaxy. Using data on the location and proper motion
of the pulsar, combined with the best information available on galactic rotation; the current value of this
effect is  . Subtracting this from the observed
. Subtracting this from the observed 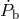 (see Table 7) gives the
corrected
(see Table 7) gives the
corrected 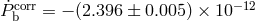 , which agrees with the prediction within the errors. In other
words,
, which agrees with the prediction within the errors. In other
words,
A third way to display the agreement with GR is by comparing the observed phase of the orbit with a
theoretical template phase as a function of time. If 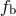 varies slowly in time, then to first order
in a Taylor expansion, the orbital phase is given by
varies slowly in time, then to first order
in a Taylor expansion, the orbital phase is given by 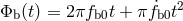 . The time of
periastron passage
. The time of
periastron passage 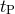 is given by
is given by  , where
, where 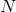 is an integer, and consequently, the
periastron time will not grow linearly with
is an integer, and consequently, the
periastron time will not grow linearly with 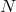 . Thus the cumulative difference between periastron
time
. Thus the cumulative difference between periastron
time 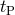 and
and 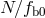 , the quantities actually measured in practice, should vary according to
, the quantities actually measured in practice, should vary according to
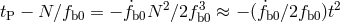 . Figure 7* shows the results: The dots are the data points,
while the curve is the predicted difference using the measured masses and the quadrupole formula for
. Figure 7* shows the results: The dots are the data points,
while the curve is the predicted difference using the measured masses and the quadrupole formula for
 [409].
[409].
The consistency among the constraints provides a test of the assumption that the two bodies behave as “point” masses, without complicated tidal effects, obeying the general relativistic equations of motion including gravitational radiation. It is also a test of strong gravity, in that the highly relativistic internal structure of the neutron stars does not influence their orbital motion, as predicted by the SEP of GR.
Observations [231, 410] indicate that the pulse profile is varying with time, which suggests that the pulsar is undergoing geodetic precession on a 300-year timescale as it moves through the curved spacetime generated by its companion (see Section 4.4.2). The amount is consistent with GR, assuming that the pulsar’s spin is suitably misaligned with the orbital angular momentum. Unfortunately, the evidence suggests that the pulsar beam may precess out of our line of sight by 2025.
6.2 A zoo of binary pulsars
More than 70 binary neutron star systems with orbital periods less than a day are now known. While some are less interesting for testing relativity, some have yielded interesting tests, and others, notably the recently discovered “double pulsar” are likely to continue to produce significant results well into the future. Here we describe some of the more interesting or best studied cases;
The “double” pulsar: J0737–3039A, B.
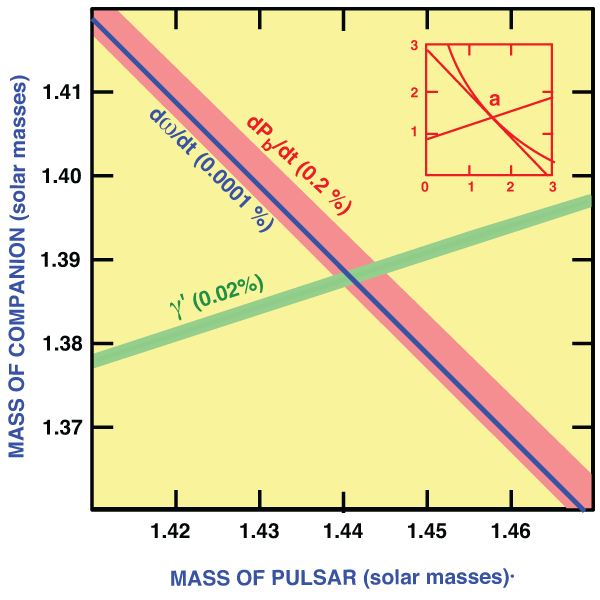
This binary pulsar system, discovered in 2003 [72], was already remarkable for its extraordinarily short orbital period (0.1 days) and large periastron advance (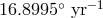 ), but then the companion was also discovered to be a pulsar [265]. Because two projected
semi-major axes could be measured, the mass ratio was obtained directly from the ratio of the two values of
), but then the companion was also discovered to be a pulsar [265]. Because two projected
semi-major axes could be measured, the mass ratio was obtained directly from the ratio of the two values of
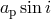 , and thereby the two masses could be obtained by combining that ratio with the periastron
advance, assuming GR. The results are
, and thereby the two masses could be obtained by combining that ratio with the periastron
advance, assuming GR. The results are  and
and 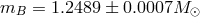 , where
, where
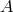 denotes the primary (first) pulsar. From these values, one finds that the orbit is nearly edge-on, with
denotes the primary (first) pulsar. From these values, one finds that the orbit is nearly edge-on, with
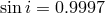 , a value which is completely consistent with that inferred from the Shapiro delay
parameter. In fact, the five measured post-Keplerian parameters plus the ratio of the projected
semi-major axes give six constraints on the masses (assuming GR): as seen in Figure 8*, all six
overlap within their measurement errors [232]. (Note that Figure 8* is based on more recent data
than that quoted in [232], in this discussion and in Table 8.) Because of the location of the
system, galactic proper-motion effects play a significantly smaller role in the interpretation
of
, a value which is completely consistent with that inferred from the Shapiro delay
parameter. In fact, the five measured post-Keplerian parameters plus the ratio of the projected
semi-major axes give six constraints on the masses (assuming GR): as seen in Figure 8*, all six
overlap within their measurement errors [232]. (Note that Figure 8* is based on more recent data
than that quoted in [232], in this discussion and in Table 8.) Because of the location of the
system, galactic proper-motion effects play a significantly smaller role in the interpretation
of  measurements than they did in B1913+16; this and the reduced effect of interstellar
dispersion means that the accuracy of measuring the gravitational-wave damping may soon
beat that from the Hulse–Taylor system. It may ultimately be necessary for the data analysis
to include second post-Newtonian (2PN) corrections, for example in the pericenter advance.
The geodetic precession of pulsar B’s spin axis has also been measured by monitoring changes
in the patterns of eclipses of the signal from pulsar A, with a result in agreement with GR
to about 13 percent [68]; the constraint on the masses from that effect (assuming GR to be
correct) is also shown in Figure 8*. In fact, pulsar B has precessed so much that its signal no
longer sweeps by the Earth, so it has gone “silent”. For a recent overview of the double pulsar,
see [71].
measurements than they did in B1913+16; this and the reduced effect of interstellar
dispersion means that the accuracy of measuring the gravitational-wave damping may soon
beat that from the Hulse–Taylor system. It may ultimately be necessary for the data analysis
to include second post-Newtonian (2PN) corrections, for example in the pericenter advance.
The geodetic precession of pulsar B’s spin axis has also been measured by monitoring changes
in the patterns of eclipses of the signal from pulsar A, with a result in agreement with GR
to about 13 percent [68]; the constraint on the masses from that effect (assuming GR to be
correct) is also shown in Figure 8*. In fact, pulsar B has precessed so much that its signal no
longer sweeps by the Earth, so it has gone “silent”. For a recent overview of the double pulsar,
see [71].
J1738+0333: A white-dwarf companion.
This is a low-eccentricity, 8.5-hour period system in which the white-dwarf companion is bright enough to permit detailed spectroscopy, allowing the companion mass to be determined directly to be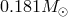 . The mass ratio is determined from
Doppler shifts of the spectral lines of the companion and of the pulsar period, giving the pulsar
mass
. The mass ratio is determined from
Doppler shifts of the spectral lines of the companion and of the pulsar period, giving the pulsar
mass 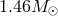 . Ten years of observation of the system yielded both a measurement of the
apparent orbital period decay, and enough information about its parallax and proper motion
to account for the substantial kinematic effect to give a value of the intrinsic period decay of
. Ten years of observation of the system yielded both a measurement of the
apparent orbital period decay, and enough information about its parallax and proper motion
to account for the substantial kinematic effect to give a value of the intrinsic period decay of
 in agreement with the predicted effect [164]. But because of the
asymmetry of the system, the result also places a significant bound on the existence of dipole radiation,
predicted by many alternative theories of gravity (see Section 6.3 below for discussion). Data from
this system were also used to place the tight bound on the PPN parameter
in agreement with the predicted effect [164]. But because of the
asymmetry of the system, the result also places a significant bound on the existence of dipole radiation,
predicted by many alternative theories of gravity (see Section 6.3 below for discussion). Data from
this system were also used to place the tight bound on the PPN parameter 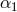 shown in
Table 4.
shown in
Table 4.
J1141–6545: A white-dwarf companion.
This system is similar in some ways to the Hulse–Taylor binary: short orbital period (0.20 days), significant orbital eccentricity (0.172), rapid periastron advance (5.3 degrees per year) and massive components (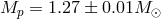 ,
, 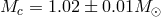 ). The key
difference is that the companion is again a white dwarf. The intrinsic orbit period decay has been
measured in agreement with GR to about six percent, again placing limits on dipole gravitational
radiation [46].
). The key
difference is that the companion is again a white dwarf. The intrinsic orbit period decay has been
measured in agreement with GR to about six percent, again placing limits on dipole gravitational
radiation [46].
J0348+0432: The most massive neutron star.
Discovered in 2011 [264, 19], this is another neutron-star white-dwarf system, in a very short period (0.1 day), low eccentricity (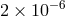 ) orbit. Timing of the
neutron star and spectroscopy of the white dwarf have led to mass values of
) orbit. Timing of the
neutron star and spectroscopy of the white dwarf have led to mass values of 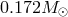 for the white dwarf
and
for the white dwarf
and 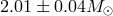 for the pulsar, making it the most massive accurately measured neutron
star yet. This supported an earlier discovery of a
for the pulsar, making it the most massive accurately measured neutron
star yet. This supported an earlier discovery of a 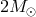 pulsar [127]; such large masses rule
out a number of heretofore viable soft equations of state for nuclear matter. The orbit period
decay agrees with the GR prediction within 20 percent and is expected to improve steadily with
time.
pulsar [127]; such large masses rule
out a number of heretofore viable soft equations of state for nuclear matter. The orbit period
decay agrees with the GR prediction within 20 percent and is expected to improve steadily with
time.
J0337+1715: Two white-dwarf companions.
This remarkable system was reported in 2014 [332]. It consists of a 2.73 millisecond pulsar (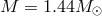 ) with extremely good timing precision, accompanied by two
white dwarfs in coplanar circular orbits. The inner white dwarf (
) with extremely good timing precision, accompanied by two
white dwarfs in coplanar circular orbits. The inner white dwarf (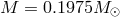 ) has an orbital period of
1.629 days, with
) has an orbital period of
1.629 days, with 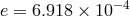 , and the outer white dwarf (
, and the outer white dwarf (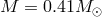 ) has a period of
327.26 days, with
) has a period of
327.26 days, with 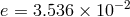 . This is an ideal system for testing the Nordtvedt effect in the
strong-field regime. Here the inner system is the analogue of the Earth-Moon system, and the outer white
dwarf plays the role of the Sun. Because the outer semi-major axis is about 1/3 of an astronomical unit, the
basic driving perturbation is comparable to that provided by the Sun. However, the self-gravitational
binding energy per unit mass of the neutron star is almost a billion times larger than that of
the Earth, greatly amplifying the size of the Nordtvedt effect. Depending on the details, this
system could exceed lunar laser ranging in testing the Nordtvedt effect by several orders of
magnitude.
. This is an ideal system for testing the Nordtvedt effect in the
strong-field regime. Here the inner system is the analogue of the Earth-Moon system, and the outer white
dwarf plays the role of the Sun. Because the outer semi-major axis is about 1/3 of an astronomical unit, the
basic driving perturbation is comparable to that provided by the Sun. However, the self-gravitational
binding energy per unit mass of the neutron star is almost a billion times larger than that of
the Earth, greatly amplifying the size of the Nordtvedt effect. Depending on the details, this
system could exceed lunar laser ranging in testing the Nordtvedt effect by several orders of
magnitude.
Other binary pulsars.
Two of the earliest binary pulsars, B1534+12 and B2127+11C, discovered in 1990, failed to live up to their early promise despite being similar to the Hulse–Taylor system in most respects (both were believed to be double neutron-star systems). The main reason was the significant uncertainty in the kinematic effect on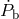 of local accelerations, galactic in the case of B1534+12, and those arising from
the globular cluster that was home to B2127+11C.
of local accelerations, galactic in the case of B1534+12, and those arising from
the globular cluster that was home to B2127+11C.
| Parameter |
J0737–3039(A, B)
|
J1738+0333
|
J1141–6545
|
| (i) Keplerian: | |||
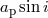 (s) (s) |
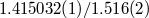 |
 |
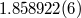 |
 |
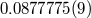 |
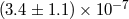 |
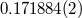 |
 (day) (day) |
 |
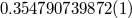 |
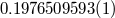 |
| (ii) Post-Keplerian: | |||
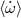 ( ( ) ) |
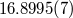 |
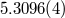 |
|
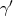 (ms) (ms) |
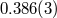 |
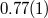 |
|
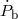 ( (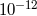 ) ) |
 |
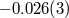 |
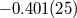 |
 ( (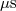 ) ) |
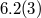 |
||
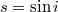 |
 |
||
6.3 Binary pulsars and alternative theories
Soon after the discovery of the binary pulsar it was widely hailed as a new testing ground for relativistic gravitational effects. As we have seen in the case of GR, in most respects, the system has lived up to, indeed exceeded, the early expectations.
In another respect, however, the system has only partially lived up to its promise, namely as a direct
testing ground for alternative theories of gravity. The origin of this promise was the discovery [139, 415]
that alternative theories of gravity generically predict the emission of dipole gravitational radiation from
binary star systems. In GR, there is no dipole radiation because the “dipole moment” (center of mass) of
isolated systems is uniform in time (conservation of momentum), and because the “inertial mass” that
determines the dipole moment is the same as the mass that generates gravitational waves (SEP). In
other theories, while the inertial dipole moment may remain uniform, the “gravity wave” dipole
moment need not, because the mass that generates gravitational waves depends differently on the
internal gravitational binding energy of each body than does the inertial mass (violation of SEP).
Schematically, in a coordinate system in which the center of inertial mass is at the origin, so that
 , the dipole part of the retarded gravitational field would be given by
, the dipole part of the retarded gravitational field would be given by
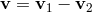 ,
, 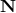 is a unit vector directed toward the observer, and
is a unit vector directed toward the observer, and 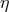 and
and 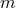 are defined using
inertial masses. In theories that violate SEP, the difference between gravitational-wave mass and inertial
mass is a function of the internal gravitational binding energy of the bodies. This additional form of
gravitational radiation damping could, at least in principle, be significantly stronger than the
usual quadrupole damping, because it depends on fewer powers of the orbital velocity
are defined using
inertial masses. In theories that violate SEP, the difference between gravitational-wave mass and inertial
mass is a function of the internal gravitational binding energy of the bodies. This additional form of
gravitational radiation damping could, at least in principle, be significantly stronger than the
usual quadrupole damping, because it depends on fewer powers of the orbital velocity  ,
and it depends on the gravitational binding energy per unit mass of the bodies, which, for
neutron stars, could be as large as 20 percent (see TEGP 10 [420*] for further details). As one
fulfillment of this promise, Will and Eardley worked out in detail the effects of dipole gravitational
radiation in the bimetric theory of Rosen, and, when the first observation of the decrease of the
orbital period was announced in 1979, the Rosen theory suffered a terminal blow. A wide class of
alternative theories also fails the binary pulsar test because of dipole gravitational radiation
(TEGP 12.3 [420*]).
,
and it depends on the gravitational binding energy per unit mass of the bodies, which, for
neutron stars, could be as large as 20 percent (see TEGP 10 [420*] for further details). As one
fulfillment of this promise, Will and Eardley worked out in detail the effects of dipole gravitational
radiation in the bimetric theory of Rosen, and, when the first observation of the decrease of the
orbital period was announced in 1979, the Rosen theory suffered a terminal blow. A wide class of
alternative theories also fails the binary pulsar test because of dipole gravitational radiation
(TEGP 12.3 [420*]).
On the other hand, the early observations of PSR 1913+16 already indicated that, in GR, the masses of
the two bodies were nearly equal, so that, in theories of gravity that are in some sense “close” to GR, dipole
gravitational radiation would not be a strong effect, because of the apparent symmetry of the system. The
Rosen theory, and others like it, are not “close” to GR, except in their predictions for the weak-field,
slow-motion regime of the solar system. When relativistic neutron stars are present, theories like
these can predict strong effects on the motion of the bodies resulting from their internal highly
relativistic gravitational structure (violations of SEP). As a consequence, the masses inferred
from observations of the periastron shift and 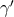 may be significantly different from those
inferred using GR, and may be different from each other, leading to strong dipole gravitational
radiation damping. By contrast, the Brans–Dicke theory is “close” to GR, roughly speaking within
may be significantly different from those
inferred using GR, and may be different from each other, leading to strong dipole gravitational
radiation damping. By contrast, the Brans–Dicke theory is “close” to GR, roughly speaking within
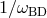 of the predictions of the latter, for large values of the coupling constant
of the predictions of the latter, for large values of the coupling constant  . Thus,
despite the presence of dipole gravitational radiation, the Hulse–Taylor binary pulsar provides
at present only a weak test of pure Brans–Dicke theory, not competitive with solar-system
tests.
. Thus,
despite the presence of dipole gravitational radiation, the Hulse–Taylor binary pulsar provides
at present only a weak test of pure Brans–Dicke theory, not competitive with solar-system
tests.
However, the discovery of binary pulsar systems with a white dwarf companion, such as J1738+0333,
J1141–6545 and J0348+0432 has made it possible to perform strong tests of the existence of dipole
radiation. This is because such systems are necessarily asymmetrical, since the gravitational binding
energy per unit mass of white dwarfs is of order 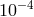 , much less than that of the neutron
star. Already, significant bounds have been placed on dipole radiation using J1738+0333 and
J1141–6545 [164, 46].
, much less than that of the neutron
star. Already, significant bounds have been placed on dipole radiation using J1738+0333 and
J1141–6545 [164, 46].
Because the gravitational-radiation and strong-field properties of alternative theories of gravity can be dramatically different from those of GR and each other, it is difficult to parametrize these aspects of the theories in the manner of the PPN framework. In addition, because of the generic violation of the strong equivalence principle in these theories, the results can be very sensitive to the equation of state and mass of the neutron star(s) in the system. In the end, there is no way around having to analyze every theory in turn. On the other hand, because of their relative simplicity, scalar–tensor theories provide an illustration of the essential effects, and so we shall discuss binary pulsars within this class of theories.
6.4 Binary pulsars and scalar–tensor gravity
Making the usual assumption that both members of the system are neutron stars, and using the methods
summarized in TEGP 10 – 12 [420*] (see also [286]) one can obtain formulas for the periastron shift, the
gravitational redshift/second-order Doppler shift parameter, the Shapiro delay coefficients, and the rate of
change of orbital period, analogous to Eqs. (108*). These formulas depend on the masses of the two neutron
stars, on their sensitivities 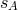 , and on the scalar–tensor parameters, as defined in Table 6 (and on a new
sensitivity
, and on the scalar–tensor parameters, as defined in Table 6 (and on a new
sensitivity 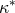 , defined below). First, there is a modification of Kepler’s third law, given by
, defined below). First, there is a modification of Kepler’s third law, given by
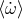 ,
, 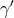 ,
,  ,
,  and
and  are
where
where
are
where
where 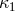 and
and  are defined in Eq. (104*). The quantity
are defined in Eq. (104*). The quantity 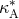 is defined by
and measures the “sensitivity” of the moment of inertia
is defined by
and measures the “sensitivity” of the moment of inertia 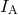 of each body to changes in the scalar field for
a fixed baryon number
of each body to changes in the scalar field for
a fixed baryon number  (see TEGP 11, 12 and 14.6 (c) [420*] for further details). The sensitivities
(see TEGP 11, 12 and 14.6 (c) [420*] for further details). The sensitivities 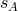 and
and  will depend on the neutron-star equation of state. Notice how the violation of SEP in
scalar–tensor theory introduces complex structure-dependent effects in everything from the Newtonian limit
(modification of the effective coupling constant in Kepler’s third law) to gravitational radiation. In the limit
will depend on the neutron-star equation of state. Notice how the violation of SEP in
scalar–tensor theory introduces complex structure-dependent effects in everything from the Newtonian limit
(modification of the effective coupling constant in Kepler’s third law) to gravitational radiation. In the limit
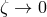 , we recover GR, and all structure dependence disappears. The first term in
, we recover GR, and all structure dependence disappears. The first term in 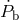 (see Eq. (114*))
is the combined effect of quadrupole and monopole gravitational radiation, post-Newtonian
corrections to dipole radiation, and a dipole-octupole coupling term, all contributing at 0PN order,
while the second term is the effect of dipole radiation, contributing at the dominant –1PN
order.
(see Eq. (114*))
is the combined effect of quadrupole and monopole gravitational radiation, post-Newtonian
corrections to dipole radiation, and a dipole-octupole coupling term, all contributing at 0PN order,
while the second term is the effect of dipole radiation, contributing at the dominant –1PN
order.
Unfortunately, because of the near equality of neutron star masses in typical double neutron star binary
pulsars, dipole radiation is somewhat suppressed, and the bounds obtained are typically not competitive
with the Cassini bound on 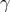 , except for those generalized scalar–tensor theories, with
, except for those generalized scalar–tensor theories, with 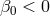 where the
strong gravity of the neutron stars induces spontaneous scalarization effects [106*]. Figure 9* illustrates this:
the bounds on
where the
strong gravity of the neutron stars induces spontaneous scalarization effects [106*]. Figure 9* illustrates this:
the bounds on 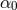 and
and 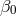 from the three binary neutron star systems B1913+16, J0737–3039, and
B1534+12 are not close to being competitive with the Cassini bound on
from the three binary neutron star systems B1913+16, J0737–3039, and
B1534+12 are not close to being competitive with the Cassini bound on 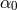 , except for very negative
values of
, except for very negative
values of 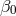 (recall that
(recall that 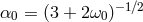 ).
).
On the other hand, a binary pulsar system with dissimilar objects, such as a white dwarf or black
hole companion, provides potentially more promising tests of dipole radiation. As a result, the
neutron-star–white-dwarf systems J1141–6545 and J1738+0333 yield much more stringent bounds. Indeed,
the latter system surpasses the Cassini bound for 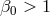 and
and  , and is close to that bound for
the pure Brans–Dicke case
, and is close to that bound for
the pure Brans–Dicke case 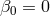 [164].
[164].
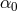 and
and 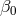 from solar-system and binary
pulsar measurements. Bounds from tests of the Nordtvedt effect using lunar laser ranging and circular
pulsar–white-dwarf binary systems are denoted LLR and SEP, respectively. Image reproduced with
permission from [164], copyright by the authors.
from solar-system and binary
pulsar measurements. Bounds from tests of the Nordtvedt effect using lunar laser ranging and circular
pulsar–white-dwarf binary systems are denoted LLR and SEP, respectively. Image reproduced with
permission from [164], copyright by the authors. It is worth pointing out that the bounds displayed in Figure 9* have been calculated using a specific
choice of scalar–tensor theory, in which the function  is given by
is given by
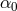 , and
, and 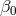 , are arbitrary parameters, and
, are arbitrary parameters, and 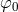 is the asymptotic value of the scalar
field. In the notation for scalar–tensor theories used here, this theory corresponds to the choice
where
is the asymptotic value of the scalar
field. In the notation for scalar–tensor theories used here, this theory corresponds to the choice
where 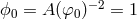 . The parameters
. The parameters 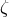 and
and 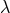 are given by
The bounds were also calculated using a polytropic equation of state, which tends to give lower maximum
masses for neutron stars than do more realistic equations of state.
are given by
The bounds were also calculated using a polytropic equation of state, which tends to give lower maximum
masses for neutron stars than do more realistic equations of state.
Bounds on various versions of TeVeS theories have also been established, with the tightest constraints
again coming from neutron-star–white-dwarf binaries [164]; in the case of TeVeS, the theory naturally
predicts 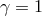 in the post-Newtonian limit, so the Cassini measurements are irrelevant here. Strong
constraints on the Einstein-Æther and Khronometric theories have also been placed using binary pulsar
measurements, exploiting both gravitational-wave damping data, and data related to preferred-frame
effects [443, 442].
in the post-Newtonian limit, so the Cassini measurements are irrelevant here. Strong
constraints on the Einstein-Æther and Khronometric theories have also been placed using binary pulsar
measurements, exploiting both gravitational-wave damping data, and data related to preferred-frame
effects [443, 442].





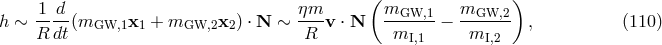

![⟨˙ω⟩ = 6πfb (2παmfb )2∕3(1 − e2)−1𝒫, (112 ) m [ m ] γ ′ = e(2πfb )−1(2παmfb )2∕3--2α −1 1 − 2ζs2 + α --2 + ζκ∗1(1 − 2s2) , (113 ) m m P˙ = − 192-π(2π αℳf )5∕3F ′(e) − 8π ζ(2πμf )𝒮2G (e), (114 ) b 5 b b r = m2 (1 − ζ), (115 ) s = sini, (116 )](article1386x.gif)
![1-( ¯ ¯ ) 𝒫 = 1 + 3 2¯γ − β+ + ψ β− , (117 ) 1 [ ( 7 1 ) 1 ( 1 ) ] F ′(e) = ---(1 − e2)−7∕2 κ1 1 + -e2 + --e4 − --κ2e2 1 + -e2 , (118 ) 12 ( ) 2 2 2 2 2 −5∕2 1 2 G (e) = (1 − e ) 1 + --e , (119 ) 2](article1387x.gif)


![[ ] A (φ) = exp α (φ − φ ) + 1β (φ − φ )2 , (121 ) 0 0 2 0 0](article1412x.gif)