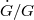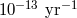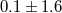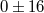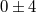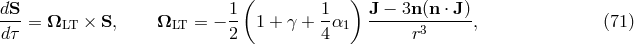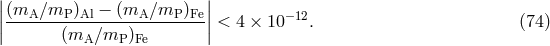4 Tests of Post-Newtonian Gravity
4.1 Tests of the parameter 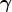
With the PPN formalism in hand, we are now ready to confront gravitation theories with the results of
solar-system experiments. In this section we focus on tests of the parameter  , consisting of the deflection
of light and the time delay of light.
, consisting of the deflection
of light and the time delay of light.
4.1.1 The deflection of light
A light ray (or photon) which passes the Sun at a distance 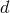 is deflected by an angle
is deflected by an angle
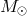 is the mass of the Sun and
is the mass of the Sun and 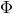 is the angle between the Earth-Sun line
and the incoming direction of the photon (see Figure 4*). For a grazing ray,
is the angle between the Earth-Sun line
and the incoming direction of the photon (see Figure 4*). For a grazing ray, 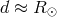 ,
, 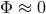 , and
independent of the frequency of light. Another, more useful expression gives the change in the relative
angular separation between an observed source of light and a nearby reference source as both rays pass near
the Sun:
where
, and
independent of the frequency of light. Another, more useful expression gives the change in the relative
angular separation between an observed source of light and a nearby reference source as both rays pass near
the Sun:
where 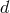 and
and 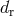 are the distances of closest approach of the source and reference rays respectively,
are the distances of closest approach of the source and reference rays respectively,
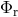 is the angular separation between the Sun and the reference source, and
is the angular separation between the Sun and the reference source, and 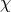 is the angle
between the Sun-source and the Sun-reference directions, projected on the plane of the sky (see
Figure 4*). Thus, for example, the relative angular separation between the two sources may vary if
the line of sight of one of them passes near the Sun (
is the angle
between the Sun-source and the Sun-reference directions, projected on the plane of the sky (see
Figure 4*). Thus, for example, the relative angular separation between the two sources may vary if
the line of sight of one of them passes near the Sun ( ,
, 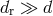 ,
, 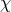 varying with
time).
varying with
time).
It is interesting to note that the classic derivations of the deflection of light that use only the
corpuscular theory of light (Cavendish 1784, von Soldner 1803 [416]), or the principle of equivalence
(Einstein 1911), yield only the “1/2” part of the coefficient in front of the expression in Eq. (61*).
But the result of these calculations is the deflection of light relative to local straight lines, as
established for example by rigid rods; however, because of space curvature around the Sun,
determined by the PPN parameter 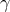 , local straight lines are bent relative to asymptotic
straight lines far from the Sun by just enough to yield the remaining factor “
, local straight lines are bent relative to asymptotic
straight lines far from the Sun by just enough to yield the remaining factor “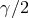 ”. The first
factor “1/2” holds in any metric theory, the second “
”. The first
factor “1/2” holds in any metric theory, the second “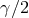 ” varies from theory to theory. Thus,
calculations that purport to derive the full deflection using the equivalence principle alone are
incorrect.
” varies from theory to theory. Thus,
calculations that purport to derive the full deflection using the equivalence principle alone are
incorrect.
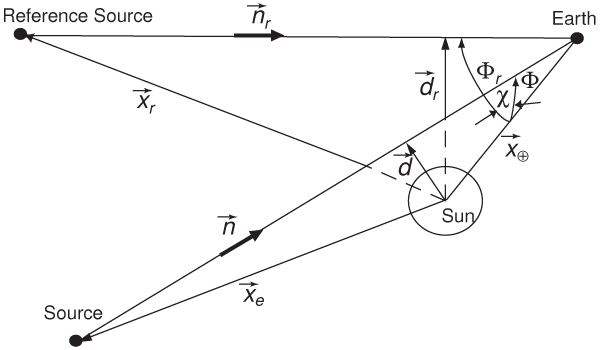
The prediction of the full bending of light by the Sun was one of the great successes of Einstein’s GR. Eddington’s confirmation of the bending of optical starlight observed during a solar eclipse in the first days following World War I helped make Einstein famous. However, the experiments of Eddington and his co-workers had only 30 percent accuracy (for a recent re-evaluation of Eddington’s conclusions, see [215]). Succeeding experiments were not much better: the results were scattered between one half and twice the Einstein value (see Figure 5*), and the accuracies were low. For a history of this period see [95].
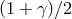 from light deflection and time delay
measurements. Its GR value is unity. The arrows at the top denote anomalously large values from
early eclipse expeditions. The Shapiro time-delay measurements using the Cassini spacecraft yielded
an agreement with GR to
from light deflection and time delay
measurements. Its GR value is unity. The arrows at the top denote anomalously large values from
early eclipse expeditions. The Shapiro time-delay measurements using the Cassini spacecraft yielded
an agreement with GR to 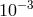 percent, and VLBI light deflection measurements have reached
0.01 percent. Hipparcos denotes the optical astrometry satellite, which reached 0.1 percent.
percent, and VLBI light deflection measurements have reached
0.01 percent. Hipparcos denotes the optical astrometry satellite, which reached 0.1 percent. However, the development of radio interferometery, and later of very-long-baseline radio
interferometry (VLBI), produced greatly improved determinations of the deflection of light.
These techniques now have the capability of measuring angular separations and changes in
angles to accuracies better than 100 microarcseconds. Early measurements took advantage of a
series of heavenly coincidences: Each year, groups of strong quasistellar radio sources pass very
close to the Sun (as seen from the Earth), including the group 3C273, 3C279, and 3C48, and
the group 0111+02, 0119+11, and 0116+08. As the Earth moves in its orbit, changing the
lines of sight of the quasars relative to the Sun, the angular separation 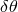 between pairs of
quasars varies (see Eq. (63*)). The time variation in the quantities
between pairs of
quasars varies (see Eq. (63*)). The time variation in the quantities  ,
, 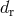 ,
, 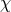 , and
, and 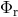 in
Eq. (63*) is determined using an accurate ephemeris for the Earth and initial directions for the
quasars, and the resulting prediction for
in
Eq. (63*) is determined using an accurate ephemeris for the Earth and initial directions for the
quasars, and the resulting prediction for 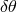 as a function of time is used as a basis for a
least-squares fit of the measured
as a function of time is used as a basis for a
least-squares fit of the measured  , with one of the fitted parameters being the coefficient
, with one of the fitted parameters being the coefficient
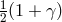 . A number of measurements of this kind over the period 1969 – 1975 yielded an accurate
determination of the coefficient
. A number of measurements of this kind over the period 1969 – 1975 yielded an accurate
determination of the coefficient 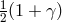 , or equivalently
, or equivalently  . A 1995 VLBI measurement
using 3C273 and 3C279 yielded
. A 1995 VLBI measurement
using 3C273 and 3C279 yielded 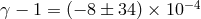 [243], while a 2009 measurement
using the VLBA targeting the same two quasars plus two other nearby radio sources yielded
[243], while a 2009 measurement
using the VLBA targeting the same two quasars plus two other nearby radio sources yielded
 [161].
[161].
In recent years, transcontinental and intercontinental VLBI observations of quasars and radio galaxies
have been made primarily to monitor the Earth’s rotation (“VLBI” in Figure 5*). These measurements are
sensitive to the deflection of light over almost the entire celestial sphere (at 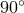 from the Sun, the
deflection is still 4 milliarcseconds). A 2004 analysis of almost 2 million VLBI observations of 541
radio sources, made by 87 VLBI sites yielded
from the Sun, the
deflection is still 4 milliarcseconds). A 2004 analysis of almost 2 million VLBI observations of 541
radio sources, made by 87 VLBI sites yielded  , or equivalently,
, or equivalently,
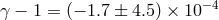 [363]. Analyses that incorporated data through 2010 yielded
[363]. Analyses that incorporated data through 2010 yielded
 [237, 238].
[237, 238].
Analysis of observations made by the Hipparcos optical astrometry satellite yielded a test at the level of 0.3 percent [165]. A VLBI measurement of the deflection of light by Jupiter was reported in 1991; the predicted deflection of about 300 microarcseconds was seen with about 50 percent accuracy [389].
Finally, a remarkable measurement of  on galactic scales was reported in 2006 [64]. It used data
on gravitational lensing by 15 elliptical galaxies, collected by the Sloan Digital Sky Survey.
The Newtonian potential
on galactic scales was reported in 2006 [64]. It used data
on gravitational lensing by 15 elliptical galaxies, collected by the Sloan Digital Sky Survey.
The Newtonian potential  of each lensing galaxy (including the contribution from dark
matter) was derived from the observed velocity dispersion of stars in the galaxy. Comparing the
observed lensing with the lensing predicted by the models provided a 10 percent bound on
of each lensing galaxy (including the contribution from dark
matter) was derived from the observed velocity dispersion of stars in the galaxy. Comparing the
observed lensing with the lensing predicted by the models provided a 10 percent bound on
 , in agreement with general relativity. Unlike the much tighter bounds described previously,
which were obtained on the scale of the solar system, this bound was obtained on a galactic
scale.
, in agreement with general relativity. Unlike the much tighter bounds described previously,
which were obtained on the scale of the solar system, this bound was obtained on a galactic
scale.
The results of light-deflection measurements are summarized in Figure 5*.
4.1.2 The time delay of light
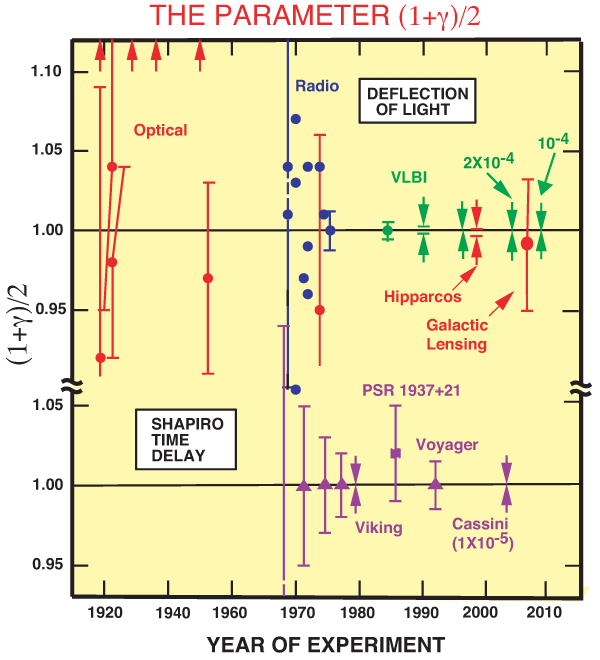
A radar signal sent across the solar system past the Sun to a planet or satellite and returned to the Earth suffers an additional non-Newtonian delay in its round-trip travel time, given by (see Figure 4*)
where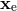 (
(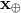 ) are the vectors, and
) are the vectors, and 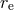 (
(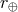 ) are the distances from the Sun to the source (Earth),
respectively (TEGP 7.2 [420*]). For a ray which passes close to the Sun,
where
) are the distances from the Sun to the source (Earth),
respectively (TEGP 7.2 [420*]). For a ray which passes close to the Sun,
where  is the distance of closest approach of the ray in solar radii, and
is the distance of closest approach of the ray in solar radii, and  is the distance of the planet
or satellite from the Sun, in astronomical units.
is the distance of the planet
or satellite from the Sun, in astronomical units.
In the two decades following Irwin Shapiro’s 1964 discovery of this effect as a theoretical consequence of
GR, several high-precision measurements were made using radar ranging to targets passing through superior
conjunction. Since one does not have access to a “Newtonian” signal against which to compare the
round-trip travel time of the observed signal, it is necessary to do a differential measurement of the
variations in round-trip travel times as the target passes through superior conjunction, and to look for the
logarithmic behavior of Eq. (65*). In order to do this accurately however, one must take into account the
variations in round-trip travel time due to the orbital motion of the target relative to the Earth. This is
done by using radar-ranging (and possibly other) data on the target taken when it is far from
superior conjunction (i.e., when the time-delay term is negligible) to determine an accurate
ephemeris for the target, using the ephemeris to predict the PPN coordinate trajectory 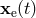 near
superior conjunction, then combining that trajectory with the trajectory of the Earth
near
superior conjunction, then combining that trajectory with the trajectory of the Earth 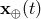 to
determine the Newtonian round-trip time and the logarithmic term in Eq. (65*). The resulting
predicted round-trip travel times in terms of the unknown coefficient
to
determine the Newtonian round-trip time and the logarithmic term in Eq. (65*). The resulting
predicted round-trip travel times in terms of the unknown coefficient 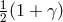 are then fit to
the measured travel times using the method of least-squares, and an estimate obtained for
are then fit to
the measured travel times using the method of least-squares, and an estimate obtained for
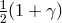 .
.
The targets employed included planets, such as Mercury or Venus, used as passive reflectors of the radar signals (“passive radar”), and artificial satellites, such as Mariners 6 and 7, Voyager 2, the Viking Mars landers and orbiters, and the Cassini spacecraft to Saturn, used as active retransmitters of the radar signals (“active radar”).
The results for the coefficient 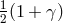 of all radar time-delay measurements performed to date
(including a measurement of the one-way time delay of signals from the millisecond pulsar PSR 1937+21)
are shown in Figure 5* (see TEGP 7.2 [420*] for discussion and references). The 1976 Viking experiment
resulted in a 0.1 percent measurement [333].
of all radar time-delay measurements performed to date
(including a measurement of the one-way time delay of signals from the millisecond pulsar PSR 1937+21)
are shown in Figure 5* (see TEGP 7.2 [420*] for discussion and references). The 1976 Viking experiment
resulted in a 0.1 percent measurement [333].
A significant improvement was reported in 2003 from Doppler tracking of the Cassini spacecraft while it
was on its way to Saturn [44], with a result 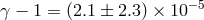 . This was made possible by the
ability to do Doppler measurements using both X-band (7175 MHz) and Ka-band (34316 MHz) radar,
thereby significantly reducing the dispersive effects of the solar corona. Note that with Doppler
measurements, one is essentially measuring the time derivative of the Shapiro delay. In addition, the 2002
superior conjunction of Cassini was particularly favorable: with the spacecraft at 8.43 astronomical
units from the Sun, the distance of closest approach of the radar signals to the Sun was only
. This was made possible by the
ability to do Doppler measurements using both X-band (7175 MHz) and Ka-band (34316 MHz) radar,
thereby significantly reducing the dispersive effects of the solar corona. Note that with Doppler
measurements, one is essentially measuring the time derivative of the Shapiro delay. In addition, the 2002
superior conjunction of Cassini was particularly favorable: with the spacecraft at 8.43 astronomical
units from the Sun, the distance of closest approach of the radar signals to the Sun was only
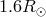 .
.
From the results of the Cassini experiment, we can conclude that the coefficient 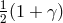 must be
within at most 0.0012 percent of unity. Massless scalar–tensor theories must have
must be
within at most 0.0012 percent of unity. Massless scalar–tensor theories must have 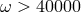 to be
compatible with this constraint.
to be
compatible with this constraint.
4.1.3 Shapiro time delay and the speed of gravity
In 2001, Kopeikin [221] suggested that a measurement of the time delay of light from a quasar as the light
passed by the planet Jupiter could be used to measure the speed of the gravitational interaction. He argued
that, since Jupiter is moving relative to the solar system, and since gravity propagates with a finite speed,
the gravitational field experienced by the light ray should be affected by gravity’s speed, since
the field experienced at one time depends on the location of the source a short time earlier,
depending on how fast gravity propagates. According to his calculations, there should be a
post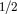 -Newtonian correction to the normal Shapiro time-delay formula (64*) which depends on the
velocity of Jupiter and on the velocity of gravity. On September 8, 2002, Jupiter passed almost in
front of a quasar, and Kopeikin and Fomalont made precise measurements of the Shapiro delay
with picosecond timing accuracy, and claimed to have measured the correction term to about
20 percent [162, 226, 222, 223*].
-Newtonian correction to the normal Shapiro time-delay formula (64*) which depends on the
velocity of Jupiter and on the velocity of gravity. On September 8, 2002, Jupiter passed almost in
front of a quasar, and Kopeikin and Fomalont made precise measurements of the Shapiro delay
with picosecond timing accuracy, and claimed to have measured the correction term to about
20 percent [162, 226, 222, 223*].
However, several authors pointed out that this 1.5PN effect does not depend on the speed of
propagation of gravity, but rather only depends on the speed of light [24, 425*, 348, 73, 349]. Intuitively, if
one is working to only first order in 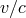 , then all that counts is the uniform motion of the planet Jupiter
(its acceleration about the Sun contributes a higher-order, unmeasurably small effect). But if that is the
case, then the principle of relativity says that one can view things from the rest frame of Jupiter. In
this frame, Jupiter’s gravitational field is static, and the speed of propagation of gravity is
irrelevant. A detailed post-Newtonian calculation of the effect was done using a variant of the
PPN framework, in a class of theories in which the speed of gravity could be different from
that of light [425*], and found explicitly that, at first order in
, then all that counts is the uniform motion of the planet Jupiter
(its acceleration about the Sun contributes a higher-order, unmeasurably small effect). But if that is the
case, then the principle of relativity says that one can view things from the rest frame of Jupiter. In
this frame, Jupiter’s gravitational field is static, and the speed of propagation of gravity is
irrelevant. A detailed post-Newtonian calculation of the effect was done using a variant of the
PPN framework, in a class of theories in which the speed of gravity could be different from
that of light [425*], and found explicitly that, at first order in 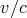 , the effect depends on the
speed of light, not the speed of gravity, in line with intuition. Effects dependent upon the speed
of gravity show up only at higher order in
, the effect depends on the
speed of light, not the speed of gravity, in line with intuition. Effects dependent upon the speed
of gravity show up only at higher order in  . Kopeikin gave a number of arguments in
opposition to this interpretation [223, 225, 224]. On the other hand, the
. Kopeikin gave a number of arguments in
opposition to this interpretation [223, 225, 224]. On the other hand, the 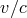 correction term does
show a dependence on the PPN parameter
correction term does
show a dependence on the PPN parameter 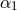 , which could be non-zero in theories of gravity
with a differing speed
, which could be non-zero in theories of gravity
with a differing speed 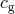 of gravity (see Eq. (7) of [425]). But existing tight bounds on
of gravity (see Eq. (7) of [425]). But existing tight bounds on 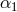 from other experiments (see Table 4) already far exceed the capability of the Jupiter VLBI
experiment.
from other experiments (see Table 4) already far exceed the capability of the Jupiter VLBI
experiment.
| Parameter |
Effect
|
Limit
|
Remarks
|
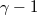 |
time delay | 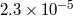 |
Cassini tracking |
| light deflection | 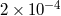 |
VLBI | |
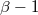 |
perihelion shift | 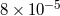 |
 |
| Nordtvedt effect | 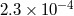 |
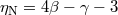 assumed assumed |
|
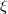 |
spin precession | 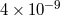 |
millisecond pulsars |
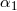 |
orbital polarization | 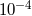 |
Lunar laser ranging |
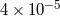 |
PSR J1738+0333 | ||
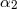 |
spin precession | 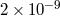 |
millisecond pulsars |
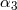 |
pulsar acceleration | 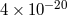 |
pulsar 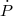 statistics statistics |
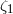 |
—
|
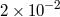 |
combined PPN bounds |
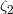 |
binary acceleration |  |
 for PSR 1913+16 for PSR 1913+16 |
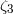 |
Newton’s 3rd law | 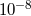 |
lunar acceleration |
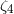 |
—
|
—
|
not independent [see Eq. (73*)] |
4.2 The perihelion shift of Mercury
The explanation of the anomalous perihelion shift of Mercury’s orbit was another of the triumphs of GR. This had been an unsolved problem in celestial mechanics for over half a century, since the announcement by Le Verrier in 1859 that, after the perturbing effects of the planets on Mercury’s orbit had been accounted for, and after the effect of the precession of the equinoxes on the astronomical coordinate system had been subtracted, there remained in the data an unexplained advance in the perihelion of Mercury. The modern value for this discrepancy is 43 arcseconds per century. A number of ad hoc proposals were made in an attempt to account for this excess, including, among others, the existence of a new planet Vulcan near the Sun, a ring of planetoids, a solar quadrupole moment and a deviation from the inverse-square law of gravitation, but none was successful. General relativity accounted for the anomalous shift in a natural way without disturbing the agreement with other planetary observations.
The predicted advance per orbit 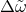 , including both relativistic PPN contributions and
the Newtonian contribution resulting from a possible solar quadrupole moment, is given by
, including both relativistic PPN contributions and
the Newtonian contribution resulting from a possible solar quadrupole moment, is given by
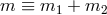 and
and 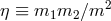 are the total mass and dimensionless reduced mass of the
two-body system respectively;
are the total mass and dimensionless reduced mass of the
two-body system respectively; 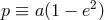 is the semi-latus rectum of the orbit, with the semi-major
axis
is the semi-latus rectum of the orbit, with the semi-major
axis  and the eccentricity
and the eccentricity  ;
; 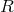 is the mean radius of the oblate body; and
is the mean radius of the oblate body; and 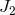 is a dimensionless
measure of its quadrupole moment, given by
is a dimensionless
measure of its quadrupole moment, given by 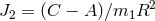 , where
, where 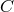 and
and 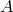 are the moments
of inertia about the body’s rotation and equatorial axes, respectively (for details of the derivation see
TEGP 7.3 [420*]). We have ignored preferred-frame and galaxy-induced contributions to
are the moments
of inertia about the body’s rotation and equatorial axes, respectively (for details of the derivation see
TEGP 7.3 [420*]). We have ignored preferred-frame and galaxy-induced contributions to 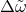 ; these are
discussed in TEGP 8.3 [420*].
; these are
discussed in TEGP 8.3 [420*].
The first term in Eq. (66*) is the classical relativistic perihelion shift, which depends upon the
PPN parameters 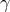 and
and 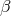 . The second term depends upon the ratio of the masses of the
two bodies; it is zero in any fully conservative theory of gravity (
. The second term depends upon the ratio of the masses of the
two bodies; it is zero in any fully conservative theory of gravity (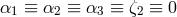 );
it is also negligible for Mercury, since
);
it is also negligible for Mercury, since  . We shall drop this term
henceforth.
. We shall drop this term
henceforth.
The third term depends upon the solar quadrupole moment 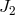 . For a Sun that rotates uniformly with
its observed surface angular velocity, so that the quadrupole moment is produced by centrifugal flattening,
one may estimate
. For a Sun that rotates uniformly with
its observed surface angular velocity, so that the quadrupole moment is produced by centrifugal flattening,
one may estimate 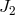 to be
to be 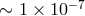 . This actually agrees reasonably well with values inferred from
rotating solar models that are in accord with observations of the normal modes of solar oscillations
(helioseismology); the latest inversions of helioseismology data give
. This actually agrees reasonably well with values inferred from
rotating solar models that are in accord with observations of the normal modes of solar oscillations
(helioseismology); the latest inversions of helioseismology data give 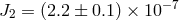 [275, 17]; for
a review of measurements of the solar quadrupole moment, see [344]. Substituting standard orbital elements
and physical constants for Mercury and the Sun we obtain the rate of perihelion shift
[275, 17]; for
a review of measurements of the solar quadrupole moment, see [344]. Substituting standard orbital elements
and physical constants for Mercury and the Sun we obtain the rate of perihelion shift  , in seconds of arc
per century,
, in seconds of arc
per century,
The most recent fits to planetary data include data from the Messenger spacecraft that orbited Mercury,
thereby significantly improving knowledge of its orbit. Adopting the Cassini bound on  a priori, these
analyses yield a bound on
a priori, these
analyses yield a bound on 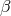 given by
given by 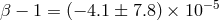 . Further analysis could push this
bound even lower [152, 399], although knowledge of
. Further analysis could push this
bound even lower [152, 399], although knowledge of 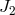 would have to improve simultaneously. A slightly
weaker bound
would have to improve simultaneously. A slightly
weaker bound 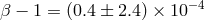 from the perihelion advance of Mars (again adopting
the Cassini bound on
from the perihelion advance of Mars (again adopting
the Cassini bound on  ) was obtained by exploiting data from the Mars Reconnaissance
Orbiter [220]
) was obtained by exploiting data from the Mars Reconnaissance
Orbiter [220]
Laser tracking of the Earth-orbiting satellite LAGEOS II led to a measurement of its relativistic perigee precession (3.4 arcseconds per year) in agreement with GR to two percent [262, 263] (note that the second paper contains an improved assessment of systematic errors).
4.3 Tests of the strong equivalence principle
The next class of solar-system experiments that test relativistic gravitational effects may be called tests of the strong equivalence principle (SEP). In Section 3.1.2 we pointed out that many metric theories of gravity (perhaps all except GR) can be expected to violate one or more aspects of SEP. Among the testable violations of SEP are a violation of the weak equivalence principle for gravitating bodies that leads to perturbations in the Earth-Moon orbit, preferred-location and preferred-frame effects in the locally measured gravitational constant that could produce observable geophysical effects, and possible variations in the gravitational constant over cosmological timescales.
4.3.1 The Nordtvedt effect and the lunar Eötvös experiment
In a pioneering calculation using his early form of the PPN formalism, Nordtvedt [304] showed that many
metric theories of gravity predict that massive bodies violate the weak equivalence principle – that is, fall
with different accelerations depending on their gravitational self-energy. Dicke [342] argued that such an
effect would occur in theories with a spatially varying gravitational constant, such as scalar–tensor gravity.
For a spherically symmetric body, the acceleration from rest in an external gravitational potential 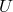 has
the form
has
the form
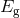 is the negative of the gravitational self-energy of the body (
is the negative of the gravitational self-energy of the body (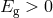 ). This violation
of the massive-body equivalence principle is known as the “Nordtvedt effect”. The effect is
absent in GR (
). This violation
of the massive-body equivalence principle is known as the “Nordtvedt effect”. The effect is
absent in GR (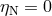 ) but present in scalar–tensor theory (
) but present in scalar–tensor theory (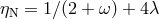 ). The
existence of the Nordtvedt effect does not violate the results of laboratory Eötvös experiments,
since for laboratory-sized objects
). The
existence of the Nordtvedt effect does not violate the results of laboratory Eötvös experiments,
since for laboratory-sized objects 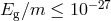 , far below the sensitivity of current or future
experiments. However, for astronomical bodies,
, far below the sensitivity of current or future
experiments. However, for astronomical bodies, 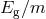 may be significant (
may be significant ( for the Sun,
for the Sun,
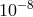 for Jupiter,
for Jupiter, 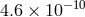 for the Earth,
for the Earth,  for the Moon). If the Nordtvedt
effect is present (
for the Moon). If the Nordtvedt
effect is present ( ) then the Earth should fall toward the Sun with a slightly different
acceleration than the Moon. This perturbation in the Earth-Moon orbit leads to a polarization of the
orbit that is directed toward the Sun as it moves around the Earth-Moon system, as seen from
Earth. This polarization represents a perturbation in the Earth-Moon distance of the form
where
) then the Earth should fall toward the Sun with a slightly different
acceleration than the Moon. This perturbation in the Earth-Moon orbit leads to a polarization of the
orbit that is directed toward the Sun as it moves around the Earth-Moon system, as seen from
Earth. This polarization represents a perturbation in the Earth-Moon distance of the form
where  and
and  are the angular frequencies of the orbits of the Moon and Sun around the Earth (see
TEGP 8.1 [420*] for detailed derivations and references; for improved calculations of the numerical
coefficient, see [309*, 120]).
are the angular frequencies of the orbits of the Moon and Sun around the Earth (see
TEGP 8.1 [420*] for detailed derivations and references; for improved calculations of the numerical
coefficient, see [309*, 120]).
Since August 1969, when the first successful acquisition was made of a laser signal reflected from the
Apollo 11 retroreflector on the Moon, the LLR experiment has made regular measurements of the
round-trip travel times of laser pulses between a network of observatories and the lunar retroreflectors, with
accuracies that are approaching the 5 ps (1 mm) level. These measurements are fit using the method of
least-squares to a theoretical model for the lunar motion that takes into account perturbations due to the
Sun and the other planets, tidal interactions, and post-Newtonian gravitational effects. The predicted
round-trip travel times between retroreflector and telescope also take into account the librations of the
Moon, the orientation of the Earth, the location of the observatories, and atmospheric effects on the signal
propagation. The “Nordtvedt” parameter 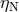 along with several other important parameters of the
model are then estimated in the least-squares method. For a review of lunar laser ranging, see
[277].
along with several other important parameters of the
model are then estimated in the least-squares method. For a review of lunar laser ranging, see
[277].
Numerous ongoing analyses of the data find no evidence, within experimental uncertainty, for the
Nordtvedt effect [436*, 437*] (for earlier results see [132*, 435*, 295*]). These results represent a
limit on a possible violation of WEP for massive bodies of about 1.4 parts in 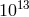 (compare
Figure 1*).
(compare
Figure 1*).
However, at this level of precision, one cannot regard the results of LLR as a “clean” test of SEP until
one eliminates the possibility of a compensating violation of WEP for the two bodies, because the chemical
compositions of the Earth and Moon differ in the relative fractions of iron and silicates. To this end, the
Eöt-Wash group carried out an improved test of WEP for laboratory bodies whose chemical compositions
mimic that of the Earth and Moon. The resulting bound of 1.4 parts in 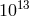 [29, 1] from composition
effects reduces the ambiguity in the LLR bound, and establishes the firm SEP test at the level of
about 2 parts in
[29, 1] from composition
effects reduces the ambiguity in the LLR bound, and establishes the firm SEP test at the level of
about 2 parts in 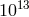 . These results can be summarized by the Nordtvedt parameter bound
. These results can be summarized by the Nordtvedt parameter bound
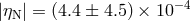 .
.
APOLLO, the Apache Point Observatory for Lunar Laser-ranging Operation, a joint effort by researchers from the Universities of Washington, Seattle, and California, San Diego, has achieved mm ranging precision using enhanced laser and telescope technology, together with a good, high-altitude site in New Mexico. However models of the lunar orbit must be improved in parallel in order to achieve an order-of-magnitude improvement in the test of the Nordtvedt effect [298]. This effort will be aided by the fortuitous 2010 discovery by the Lunar Reconnaissance Orbiter of the precise landing site of the Soviet Lunokhod I rover, which deployed a retroreflector in 1970. Its uncertain location made it effectively “lost” to lunar laser ranging for almost 40 years. Its location on the lunar surface will make it useful in improving models of the lunar libration [297].
In GR, the Nordtvedt effect vanishes; at the level of several centimeters and below, a number of non-null general relativistic effects should be present [309].
Tests of the Nordtvedt effect for neutron stars have also been carried out using a class of systems known
as wide-orbit binary millisecond pulsars (WBMSP), which are pulsar–white-dwarf binary systems with
small orbital eccentricities. In the gravitational field of the galaxy, a non-zero Nordtvedt effect can
induce an apparent anomalous eccentricity pointed toward the galactic center [118], which
can be bounded using statistical methods, given enough WBMSPs (see [374*] for a review and
references). Using data from 21 WBMSPs, including recently discovered highly circular systems,
Stairs et al. [375*] obtained the bound 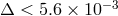 , where
, where  . Because
. Because
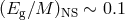 for typical neutron stars, this bound does not compete with the bound on
for typical neutron stars, this bound does not compete with the bound on
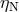 from LLR; on the other hand, it does test SEP in the strong-field regime because of the
presence of the neutron stars. The 2013 discovery of a millisecond pulsar in orbit with two white
dwarfs in very circular, coplanar orbits [332] may lead to a test of the Nordvedt effect in the
strong-field regime that surpasses the precision of lunar laser ranging by a substantial factor (see
Section 6.2).
from LLR; on the other hand, it does test SEP in the strong-field regime because of the
presence of the neutron stars. The 2013 discovery of a millisecond pulsar in orbit with two white
dwarfs in very circular, coplanar orbits [332] may lead to a test of the Nordvedt effect in the
strong-field regime that surpasses the precision of lunar laser ranging by a substantial factor (see
Section 6.2).
4.3.2 Preferred-frame and preferred-location effects
Some theories of gravity violate SEP by predicting that the outcomes of local gravitational experiments
may depend on the velocity of the laboratory relative to the mean rest frame of the universe
(preferred-frame effects) or on the location of the laboratory relative to a nearby gravitating body
(preferred-location effects). In the post-Newtonian limit, preferred-frame effects are governed by the values
of the PPN parameters 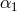 ,
, 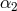 , and
, and  , and some preferred-location effects are governed by
, and some preferred-location effects are governed by 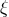 (see
Table 2).
(see
Table 2).
The most important such effects are variations and anisotropies in the locally-measured value of the gravitational constant which lead to anomalous Earth tides and variations in the Earth’s rotation rate, anomalous contributions to the orbital dynamics of planets and the Moon, self-accelerations of pulsars, anomalous torques on the Sun that would cause its spin axis to be randomly oriented relative to the ecliptic (see TEGP 8.2, 8.3, 9.3, and 14.3 (c) [420*]), and torques on spinning pulsars that could be seen in variations in their pulse profiles.
A tight bound on  of
of 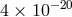 was obtained by placing limits on anomalous eccentricities in the
orbits of a number of binary millisecond pulsars [37, 375]. The best bound on
was obtained by placing limits on anomalous eccentricities in the
orbits of a number of binary millisecond pulsars [37, 375]. The best bound on 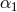 , comes from the orbit of
the pulsar–white-dwarf system J1738+0333 [359]. Early bounds on on
, comes from the orbit of
the pulsar–white-dwarf system J1738+0333 [359]. Early bounds on on 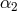 and
and 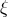 came from searches
for variations induced by an anisotropy in
came from searches
for variations induced by an anisotropy in 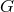 on the acceleration of gravity on Earth using
gravimeters, and (in the case of
on the acceleration of gravity on Earth using
gravimeters, and (in the case of 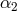 ) from limiting the effects of any anomalous torque on the
spinning Sun over the age of the solar system. Today the best bounds on
) from limiting the effects of any anomalous torque on the
spinning Sun over the age of the solar system. Today the best bounds on 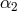 and
and 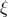 come from
bounding torques on the solitary millisecond pulsars B1937+21 and J1744–1134 [358, 360].
Because these later bounds involve systems with strong internal gravity of the neutron stars,
they should strictly speaking be regarded as bounds on “strong field” analogues of the PPN
parameters. Here we will treat them as bounds on the standard PPN parameters, as shown in
Table 4.
come from
bounding torques on the solitary millisecond pulsars B1937+21 and J1744–1134 [358, 360].
Because these later bounds involve systems with strong internal gravity of the neutron stars,
they should strictly speaking be regarded as bounds on “strong field” analogues of the PPN
parameters. Here we will treat them as bounds on the standard PPN parameters, as shown in
Table 4.
4.3.3 Constancy of the Newtonian gravitational constant
Most theories of gravity that violate SEP predict that the locally measured Newtonian gravitational
constant may vary with time as the universe evolves. For the scalar–tensor theories listed in Table 3, the
predictions for 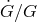 can be written in terms of time derivatives of the asymptotic scalar field. Where
can be written in terms of time derivatives of the asymptotic scalar field. Where  does change with cosmic evolution, its rate of variation should be of the order of the expansion rate
of the universe, i.e.,
does change with cosmic evolution, its rate of variation should be of the order of the expansion rate
of the universe, i.e., 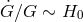 , where
, where  is the Hubble expansion parameter, given by
is the Hubble expansion parameter, given by
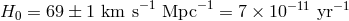 [39].
[39].
Several observational constraints can be placed on 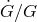 , one kind coming from bounding the present
rate of variation, another from bounding a difference between the present value and a past value. The first
type of bound typically comes from LLR measurements, planetary radar-ranging measurements, and pulsar
timing data. The second type comes from studies of the evolution of the Sun, stars and the Earth,
Big-Bang nucleosynthesis, and analyses of ancient eclipse data. Recent results are shown in
Table 5.
, one kind coming from bounding the present
rate of variation, another from bounding a difference between the present value and a past value. The first
type of bound typically comes from LLR measurements, planetary radar-ranging measurements, and pulsar
timing data. The second type comes from studies of the evolution of the Sun, stars and the Earth,
Big-Bang nucleosynthesis, and analyses of ancient eclipse data. Recent results are shown in
Table 5.
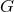 .
. The best limits on a current 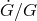 come from improvements in the ephemeris of Mars using range and
Doppler data from the Mars Global Surveyor (1998 – 2006), Mars Odyssey (2002 – 2008), and Mars
Reconnaissance Orbiter (2006 – 2008), together with improved data and modeling of the effects of the
asteroid belt [321, 220]. Since the bound is actually on variations of
come from improvements in the ephemeris of Mars using range and
Doppler data from the Mars Global Surveyor (1998 – 2006), Mars Odyssey (2002 – 2008), and Mars
Reconnaissance Orbiter (2006 – 2008), together with improved data and modeling of the effects of the
asteroid belt [321, 220]. Since the bound is actually on variations of  , any future improvements in
, any future improvements in
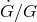 beyond a part in
beyond a part in 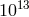 will have to take into account models of the actual mass loss from the Sun,
due to radiation of photons and neutrinos (
will have to take into account models of the actual mass loss from the Sun,
due to radiation of photons and neutrinos (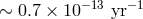 ) and due to the solar wind
(
) and due to the solar wind
(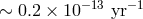 ). Another bound comes from LLR measurements ([436*]; for earlier results
see [132*, 435*, 295]).
). Another bound comes from LLR measurements ([436*]; for earlier results
see [132*, 435*, 295]).
Although bounds on 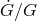 from solar-system measurements can be correctly obtained in a
phenomenological manner through the simple expedient of replacing
from solar-system measurements can be correctly obtained in a
phenomenological manner through the simple expedient of replacing 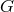 by
by 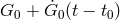 in Newton’s
equations of motion, the same does not hold true for pulsar and binary pulsar timing measurements. The
reason is that, in theories of gravity that violate SEP, such as scalar–tensor theories, the “mass” and
moment of inertia of a gravitationally bound body may vary with
in Newton’s
equations of motion, the same does not hold true for pulsar and binary pulsar timing measurements. The
reason is that, in theories of gravity that violate SEP, such as scalar–tensor theories, the “mass” and
moment of inertia of a gravitationally bound body may vary with 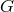 . Because neutron stars are highly
relativistic, the fractional variation in these quantities can be comparable to
. Because neutron stars are highly
relativistic, the fractional variation in these quantities can be comparable to 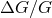 , the precise variation
depending both on the equation of state of neutron star matter and on the theory of gravity in the
strong-field regime. The variation in the moment of inertia affects the spin rate of the pulsar, while the
variation in the mass can affect the orbital period in a manner that can subtract from the direct
effect of a variation in
, the precise variation
depending both on the equation of state of neutron star matter and on the theory of gravity in the
strong-field regime. The variation in the moment of inertia affects the spin rate of the pulsar, while the
variation in the mass can affect the orbital period in a manner that can subtract from the direct
effect of a variation in 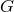 , given by
, given by 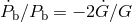 [308]. Thus, the bounds quoted in
Table 5 for binary and millisecond pulsars are theory-dependent and must be treated as merely
suggestive.
[308]. Thus, the bounds quoted in
Table 5 for binary and millisecond pulsars are theory-dependent and must be treated as merely
suggestive.
In a similar manner, bounds from helioseismology and Big-Bang nucleosynthesis (BBN) assume a
model for the evolution of 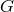 over the multi-billion year time spans involved. For example, the
concordance of predictions for light elements produced around 3 minutes after the Big Bang
with the abundances observed indicate that
over the multi-billion year time spans involved. For example, the
concordance of predictions for light elements produced around 3 minutes after the Big Bang
with the abundances observed indicate that 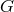 then was within 20 percent of
then was within 20 percent of 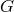 today.
Assuming a power-law variation of
today.
Assuming a power-law variation of  then yields a bound on
then yields a bound on 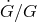 today shown in
Table 5.
today shown in
Table 5.
4.4 Other tests of post-Newtonian gravity
4.4.1 Search for gravitomagnetism
According to GR, moving or rotating matter should produce a contribution to the gravitational field that is
the analogue of the magnetic field of a moving charge or a magnetic dipole. In particular, one can view the
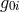 part of the PPN metric (see Box 2) as an analogue of the vector potential of electrodynamics. In a
suitable gauge (not the standard PPN gauge), and dropping the preferred-frame terms, it can be written
part of the PPN metric (see Box 2) as an analogue of the vector potential of electrodynamics. In a
suitable gauge (not the standard PPN gauge), and dropping the preferred-frame terms, it can be written
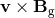 to the equation of motion, where the
gravitomagnetic field
to the equation of motion, where the
gravitomagnetic field 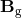 is given by
is given by 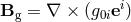 .
.
Gravitomagnetism plays a role in a variety of measured relativistic effects involving moving material sources, such as the Earth-Moon system and binary pulsar systems. Nordtvedt [307, 306] has argued that, if the gravitomagnetic potential (70*) were turned off, then there would be anomalous orbital effects in LLR and binary pulsar data.
Rotation also produces a gravitomagnetic effect, since for a rotating body, 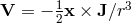 , where
, where
 is the angular momentum of the body. The result is a “dragging of inertial frames” around the body,
also called the Lense–Thirring effect. A consequence is a precession of a gyroscope’s spin
is the angular momentum of the body. The result is a “dragging of inertial frames” around the body,
also called the Lense–Thirring effect. A consequence is a precession of a gyroscope’s spin 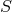 according to
according to
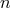 is a unit radial vector, and
is a unit radial vector, and  is the distance from the center of the body (TEGP 9.1 [420*]).
is the distance from the center of the body (TEGP 9.1 [420*]).
In 2011 the Relativity Gyroscope Experiment (Gravity Probe B or GPB) carried out by Stanford University, NASA and Lockheed Martin Corporation [177], finally completed a space mission to detect this frame-dragging or Lense–Thirring precession, along with the “geodetic” precession (see Section 4.4.2). Gravity Probe B will very likely go down in the history of science as one of the most ambitious, difficult, expensive, and controversial relativity experiments ever performed.2 It was almost 50 years from inception to completion, although only about half of that time was spent as a full-fledged, approved space program.
The GPB spacecraft was launched on April 20, 2004 into an almost perfectly circular polar orbit at an
altitude of 642 km, with the orbital plane parallel to the direction of a guide star known as IM Pegasi
(HR 8703). The spacecraft contained four spheres made of fuzed quartz, all spinning about the same axis
(two were spun in the opposite direction), which was oriented to be in the orbital plane, pointing toward the
guide star. An onboard telescope pointed continuously at the guide star, and the direction of each spin was
compared with the direction to the star, which was at a declination of 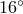 relative to the Earth’s
equatorial plane. With these conditions, the precessions predicted by GR were 6630 milliarcsecond per year
for the geodetic effect, and 38 milliarcsecond per year for frame dragging, the former in the
orbital plane (in the north-south direction) and the latter perpendicular to it (in the east-west
direction).
relative to the Earth’s
equatorial plane. With these conditions, the precessions predicted by GR were 6630 milliarcsecond per year
for the geodetic effect, and 38 milliarcsecond per year for frame dragging, the former in the
orbital plane (in the north-south direction) and the latter perpendicular to it (in the east-west
direction).
In order to reduce the non-relativistic torques on the rotors to an acceptable level, the rotors were fabricated to be both spherical and homogenous to better than a few parts in 10 million. Each rotor was coated with a thin film of niobium, and the experiment was conducted at cryogenic temperatures inside a dewar containing 2200 litres of superfluid liquid helium. As the niobium film becomes a superconductor, each rotor develops a magnetic moment parallel to its spin axis. Variations in the direction of the magnetic moment relative to the spacecraft were then measured using superconducting current loops surrounding each rotor. As the spacecraft orbits the Earth, the aberration of light from the guide star causes an artificial but predictable change in direction between the rotors and the on-board telescope; this was an essential tool for calibrating the conversion between the voltages read by the current loops and the actual angle between the rotors and the guide star. The motion of the guide star relative to distant inertial frames was measured before, during and after the mission separately by radio astronomers at Harvard/SAO and elsewhere using VLBI (IM Pegasi is a radio star) [362].
The mission ended in September 2005, as scheduled, when the last of the liquid helium boiled off. Although all subsystems of the spacecraft and the apparatus performed extremely well, they were not perfect. Calibration measurements carried out during the mission, both before and after the science phase, revealed unexpectedly large torques on the rotors. Numerous diagnostic tests worthy of a detective novel showed that these were caused by electrostatic interactions between surface imperfections (“patch effect”) on the niobium films and the spherical housings surrounding each rotor. These effects and other anomalies greatly contaminated the data and complicated its analysis, but finally, in October 2010, the Gravity Probe B team announced that the experiment had successfully measured both the geodetic and frame-dragging precessions. The outcome was in agreement with general relativity, with a precision of 0.3 percent for the geodetic precession, and 20 percent for the frame-dragging effect [149]. For a commentary on the GPB result, see [429]. The full technical and data analysis details of GPB are expected to be published as a special issue of Classical and Quantum Gravity in 2015.
Another way to look for frame-dragging is to measure the precession of orbital planes of bodies circling a rotating body. One implementation of this idea is to measure the relative precession, at about 31 milliarcseconds per year, of the line of nodes of a pair of laser-ranged geodynamics satellites (LAGEOS), ideally with supplementary inclination angles; the inclinations must be supplementary in order to cancel the dominant (126 degrees per year) nodal precession caused by the Earth’s Newtonian gravitational multipole moments. Unfortunately, the two existing LAGEOS satellites are not in appropriately inclined orbits. Nevertheless, Ciufolini and collaborators [86, 88, 85] combined nodal precession data from LAGEOS I and II with improved models for the Earth’s multipole moments provided by two orbiting geodesy satellites, Europe’s CHAMP (Challenging Minisatellite Payload) and NASA’s GRACE (Gravity Recovery and Climate Experiment), and reported a 10 percent confirmation of GR [85]. In earlier reports, Ciufolini et al. had reported tests at the the 20 – 30 percent level, without the benefit of the GRACE/CHAMP data [83, 87, 82]. Some authors stressed the importance of adequately assessing systematic errors in the LAGEOS data [338, 197].
On February 13, 2012, a third laser-ranged satellite, known as LARES (Laser Relativity Satellite) was
launched by the Italian Space Agency [315]. Its inclination was very close to the required supplementary
angle relative to LAGEOS I, and its eccentricity was very nearly zero. However, because its semimajor axis
is only 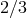 that of either LAGEOS I or II, and because the Newtonian precession rate is
proportional to
that of either LAGEOS I or II, and because the Newtonian precession rate is
proportional to 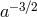 , LARES does not provide a cancellation of the Newtonian precession.
Nevertheless, combining data from all three satellites with continually improving Earth data
from GRACE, the LARES team hopes to achieve a test of frame-dragging at the one percent
level [84].
, LARES does not provide a cancellation of the Newtonian precession.
Nevertheless, combining data from all three satellites with continually improving Earth data
from GRACE, the LARES team hopes to achieve a test of frame-dragging at the one percent
level [84].
4.4.2 Geodetic precession
A gyroscope moving through curved spacetime suffers a precession of its spin axis given by
where is the velocity of the gyroscope, and
is the velocity of the gyroscope, and 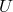 is the Newtonian gravitational potential of the source
(TEGP 9.1 [420*]). The Earth-Moon system can be considered as a “gyroscope”, with its axis
perpendicular to the orbital plane. The predicted precession is about 2 arcseconds per century, an effect
first calculated by de Sitter. This effect has been measured to about 0.6 percent using LLR
data [132, 435, 436].
is the Newtonian gravitational potential of the source
(TEGP 9.1 [420*]). The Earth-Moon system can be considered as a “gyroscope”, with its axis
perpendicular to the orbital plane. The predicted precession is about 2 arcseconds per century, an effect
first calculated by de Sitter. This effect has been measured to about 0.6 percent using LLR
data [132, 435, 436].
For the GPB gyroscopes orbiting the Earth, the precession is 6.63 arcseconds per year. GPB measured
this effect to 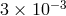 ; the resulting bound on the parameter
; the resulting bound on the parameter 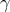 is not competitive with the Cassini
bound.
is not competitive with the Cassini
bound.
4.4.3 Tests of post-Newtonian conservation laws
Of the five “conservation law” PPN parameters 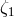 ,
, 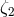 ,
, 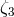 ,
, 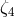 , and
, and 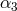 , only three,
, only three,
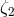 ,
, 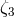 , and
, and 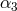 , have been constrained directly with any precision;
, have been constrained directly with any precision; 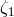 is constrained
indirectly through its appearance in the Nordtvedt effect parameter
is constrained
indirectly through its appearance in the Nordtvedt effect parameter 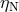 , Eq. (68*). There is strong
theoretical evidence that
, Eq. (68*). There is strong
theoretical evidence that  , which is related to the gravity generated by fluid pressure, is
not really an independent parameter – in any reasonable theory of gravity there should be a
connection between the gravity produced by kinetic energy (
, which is related to the gravity generated by fluid pressure, is
not really an independent parameter – in any reasonable theory of gravity there should be a
connection between the gravity produced by kinetic energy (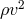 ), internal energy (
), internal energy (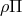 ), and
pressure (
), and
pressure (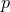 ). From such considerations, there follows [414] the additional theoretical constraint
). From such considerations, there follows [414] the additional theoretical constraint
A non-zero value for any of these parameters would result in a violation of conservation of momentum, or of Newton’s third law in gravitating systems. An alternative statement of Newton’s third law for gravitating systems is that the “active gravitational mass”, that is the mass that determines the gravitational potential exhibited by a body, should equal the “passive gravitational mass”, the mass that determines the force on a body in a gravitational field. Such an equality guarantees the equality of action and reaction and of conservation of momentum, at least in the Newtonian limit.
A classic test of Newton’s third law for gravitating systems was carried out in 1968 by Kreuzer, in which
the gravitational attraction of fluorine and bromine were compared to a precision of 5 parts in
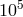 .
.
A remarkable planetary test was reported by Bartlett and van Buren [33]. They noted that current
understanding of the structure of the Moon involves an iron-rich, aluminum-poor mantle whose center
of mass is offset about 10 km from the center of mass of an aluminum-rich, iron-poor crust.
The direction of offset is toward the Earth, about  to the east of the Earth-Moon line.
Such a model accounts for the basaltic maria which face the Earth, and the aluminum-rich
highlands on the Moon’s far side, and for a 2 km offset between the observed center of mass and
center of figure for the Moon. Because of this asymmetry, a violation of Newton’s third law
for aluminum and iron would result in a momentum non-conserving self-force on the Moon,
whose component along the orbital direction would contribute to the secular acceleration of the
lunar orbit. Improved knowledge of the lunar orbit through LLR, and a better understanding
of tidal effects in the Earth-Moon system (which also contribute to the secular acceleration)
through satellite data, severely limit any anomalous secular acceleration, with the resulting limit
to the east of the Earth-Moon line.
Such a model accounts for the basaltic maria which face the Earth, and the aluminum-rich
highlands on the Moon’s far side, and for a 2 km offset between the observed center of mass and
center of figure for the Moon. Because of this asymmetry, a violation of Newton’s third law
for aluminum and iron would result in a momentum non-conserving self-force on the Moon,
whose component along the orbital direction would contribute to the secular acceleration of the
lunar orbit. Improved knowledge of the lunar orbit through LLR, and a better understanding
of tidal effects in the Earth-Moon system (which also contribute to the secular acceleration)
through satellite data, severely limit any anomalous secular acceleration, with the resulting limit
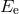 of an atomic nucleus could make a
contribution to the ratio of active to passive mass of the form
The resulting limit on
of an atomic nucleus could make a
contribution to the ratio of active to passive mass of the form
The resulting limit on 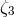 from the lunar experiment is
from the lunar experiment is 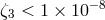 (TEGP 9.2, 14.3 (d) [420*]).
Nordtvedt [310] has examined whether this bound could be improved by considering the asymmetric
distribution of ocean water on Earth.
(TEGP 9.2, 14.3 (d) [420*]).
Nordtvedt [310] has examined whether this bound could be improved by considering the asymmetric
distribution of ocean water on Earth.
Another consequence of a violation of conservation of momentum is a self-acceleration of the center of mass of a binary stellar system, given by
where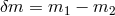 ,
,  is the semi-major axis, and
is the semi-major axis, and 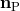 is a unit vector directed from the center of
mass to the point of periastron of
is a unit vector directed from the center of
mass to the point of periastron of 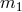 (TEGP 9.3 [420*]). A consequence of this acceleration would be
non-vanishing values for
(TEGP 9.3 [420*]). A consequence of this acceleration would be
non-vanishing values for  , where
, where  denotes the period of any intrinsic process in the system
(orbit, spectra, pulsar periods). The observed upper limit on
denotes the period of any intrinsic process in the system
(orbit, spectra, pulsar periods). The observed upper limit on 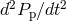 of the binary pulsar PSR 1913+16
places a strong constraint on such an effect, resulting in the bound
of the binary pulsar PSR 1913+16
places a strong constraint on such an effect, resulting in the bound  . Since
. Since 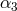 has
already been constrained to be much less than this (see Table 4), we obtain a strong solitary bound on
has
already been constrained to be much less than this (see Table 4), we obtain a strong solitary bound on
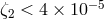 [419].
[419].
4.5 Prospects for improved PPN parameter values
A number of advanced experiments or space missions are under development or have been proposed which
could lead to significant improvements in values of the PPN parameters, of  of the Sun, and of
of the Sun, and of
 .
.
LLR at the Apache Point Observatory (APOLLO project) could improve bounds on the Nordvedt
parameter to the level 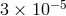 and on
and on  to better than
to better than 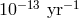 [437].
[437].
The BepiColumbo Mercury orbiter is a joint project of the European and Japanese space agencies,
scheduled for launch in 2015 [38]. In a two-year experiment, with 6 cm range capability, it could yield
improvements in 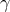 to
to 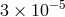 , in
, in 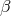 to
to 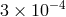 , in
, in  to
to 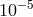 , in
, in  to
to 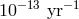 , and
in
, and
in 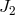 to
to 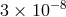 . An eight-year mission could yield further improvements by factors of 2 – 5 in
. An eight-year mission could yield further improvements by factors of 2 – 5 in 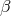 ,
,
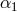 , and
, and 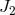 , and a further factor 15 in
, and a further factor 15 in 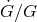 [282, 27].
[282, 27].
GAIA is a high-precision astrometric orbiting telescope launched by ESA in 2013 (a successor to
Hipparcos) [169]. With astrometric capability ranging from 10 to a few hundred microsarcseconds, plus the
ability measure the locations of a billion stars down to 20th magnitude, it could measure light-deflection
and 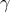 to the
to the 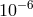 level [281].
level [281].
LATOR (Laser Astrometric Test of Relativity) is a concept for a NASA mission in which two
microsatellites orbit the Sun on Earth-like orbits near superior conjunction, so that their lines of sight are
close to the Sun. Using optical tracking and an optical interferometer on the International Space Station, it
may be possible to measure the deflection of light with sufficient accuracy to bound  to a part
in
to a part
in 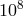 and
and 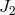 to a part in
to a part in 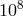 , and to measure the solar frame-dragging effect to one
percent [393, 394].
, and to measure the solar frame-dragging effect to one
percent [393, 394].
Another concept, proposed for a European Space Agency medium-class mission, is ASTROD I
(Astrodynamical Space Test of Relativity using Optical Devices), a variant of LATOR involving
a single satellite parked on the far side of the Sun [66]. Its goal is to measure 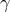 to a few
parts in
to a few
parts in 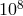 ,
, 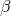 to six parts in
to six parts in  and
and 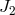 to a part in
to a part in  . A possible follow-on
mission, ASTROD-GW, involving three spacecraft, would improve on measurements of those
parameters and would also measure the solar frame-dragging effect, as well as look for gravitational
waves.
. A possible follow-on
mission, ASTROD-GW, involving three spacecraft, would improve on measurements of those
parameters and would also measure the solar frame-dragging effect, as well as look for gravitational
waves.

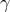


![[ ( )] 1- 4M-⊙- 4M-⊙- 1 +-cosΦr- δ𝜃 = 2(1 + γ) − d cosχ + dr 2 , (63 )](article775x.gif)
![[ ( 2 )] δt ≈ 1-(1 + γ) 240 − 20 ln d-- μs, (65 ) 2 r](article814x.gif)
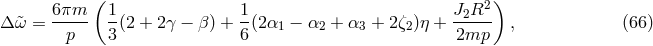
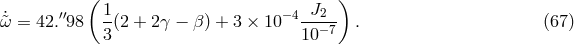
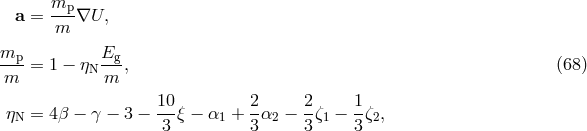
![δr = 13.1η cos(ω − ω )t [m ], (69 ) N 0 s](article902x.gif)