9 Evolution of Interacting Double-Degenerate Systems
As shown in the flowchart in Figure 9* and mentioned above, there are several ways to form a semidetached system in which a WD stably accretes matter from another WD or a helium star. This happens due to orbital angular momentum losses via GWR, since for the WD binary, orbital angular momentum loss is the only driver of orbital evolution, and low-mass helium stars (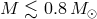 ) almost do not expand in the course of core He-burning. These stars, also
referred to as “interacting double-degenerates” (IDD), are observationally identified with the
ultra-short-period cataclysmic variables (
) almost do not expand in the course of core He-burning. These stars, also
referred to as “interacting double-degenerates” (IDD), are observationally identified with the
ultra-short-period cataclysmic variables (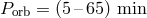 ) of the AM CVn class. We shall use below
both the terms “AM CVn stars” and “IDD”. A distinctive peculiarity of AM CVn stars is the
absence of signs of hydrogen in their spectra (with one possible exception), which suggests that
donor stars in these binaries are devoid of hydrogen. The absence of hydrogen seems to be
reliable, since the threshold for its detection is quite low:
) of the AM CVn class. We shall use below
both the terms “AM CVn stars” and “IDD”. A distinctive peculiarity of AM CVn stars is the
absence of signs of hydrogen in their spectra (with one possible exception), which suggests that
donor stars in these binaries are devoid of hydrogen. The absence of hydrogen seems to be
reliable, since the threshold for its detection is quite low: 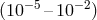 by the number of
atoms [842, 726, 463].
by the number of
atoms [842, 726, 463].
Note that apart from “double-degenerate” and “helium-star” channels for the formation of
AM CVn-stars, there exists the third, “CV”-channel [778, 779, 522, 596]. In the latter, the
donor star fills its Roche lobe at the very end of the main-sequence stage (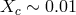 ) or just
after its completion. For such donors the chemical inhomogeneity inhibits complete mixing at
) or just
after its completion. For such donors the chemical inhomogeneity inhibits complete mixing at
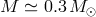 typical for initially non-evolved donors. The mixing is delayed to lower masses, and
as a result the donors become helium dwarfs with some traces of hydrogen. After reaching
the minimum orbital periods
typical for initially non-evolved donors. The mixing is delayed to lower masses, and
as a result the donors become helium dwarfs with some traces of hydrogen. After reaching
the minimum orbital periods 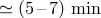 , these binaries start to evolve to longer orbital
periods. However, in this scenario the birth rate of systems that can penetrate the range of
periods occupied by the observed AM CVn-stars, especially
, these binaries start to evolve to longer orbital
periods. However, in this scenario the birth rate of systems that can penetrate the range of
periods occupied by the observed AM CVn-stars, especially 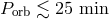 , is much lower than
the birth rate in the “double-degenerate” and “helium-star” channels; below we shall neglect
it.
, is much lower than
the birth rate in the “double-degenerate” and “helium-star” channels; below we shall neglect
it.
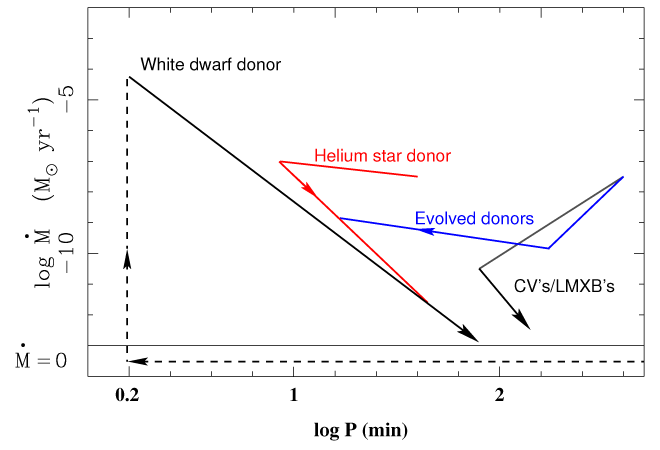
Schematically, the tracks of three families of AM CVn stars are shown in Figure 21* and compared to the track for an “ordinary” CV.
9.1 “Double-degenerate family” of AM CVn stars
The importance of AM CVn stars both for astrophysics and for physics in general stems from the fact that, because of their very short orbital periods and relative brightness due to proximity to the Sun, they are expected to be strong GWR sources and the first Galactic objects discovered by space GW interferometers like LISA (or eLISA), i.e., they will serve as “verification binaries” [744*]. Besides, AM CVn stars can be precursors of SN Ia [784*, 727*, 662] as well as still-hypothetical order-of-magnitude–weaker explosive events called SN .Ia [48, 697, 702, 576].
A comprehensive review paper on AM CVn stars covering their observational properties and some theoretical aspects was published recently by Solheim [725]. Therefore, we shall provide below only basic information about these binaries.
In a binary with stable mass transfer, change of the radius of the donor exactly matches the change of
its Roche lobe. This condition combined with the approximate size of the Roche lobe given by Eq. (35*)
(which is valid for low  ) provides the following relation between the orbital period of the binary
) provides the following relation between the orbital period of the binary 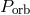 and the mass
and the mass 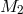 and radius
and radius 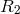 of the donor:
of the donor:
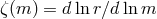 . For the mass transfer to be stable, the term in brackets must be positive, i.e.,
Violation of this criterion results in mass loss by the WD donor on a time scale comparable to 10 – 100
orbital periods, as discussed in Section 7 and most probably, in the merging of components, if a
supernova explosion is avoided. Of course, Eq. (71*) oversimplifies the conditions for a stable mass
exchange. A rigorous treatment must include tidal effects, angular momentum exchange, and
the possible super-Eddington
. For the mass transfer to be stable, the term in brackets must be positive, i.e.,
Violation of this criterion results in mass loss by the WD donor on a time scale comparable to 10 – 100
orbital periods, as discussed in Section 7 and most probably, in the merging of components, if a
supernova explosion is avoided. Of course, Eq. (71*) oversimplifies the conditions for a stable mass
exchange. A rigorous treatment must include tidal effects, angular momentum exchange, and
the possible super-Eddington 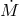 immediately after RLOF by the donor and the associated
common envelope formation, as well as the possible ignition of accreted helium on the WD
surface [829*, 269, 464*, 246].
immediately after RLOF by the donor and the associated
common envelope formation, as well as the possible ignition of accreted helium on the WD
surface [829*, 269, 464*, 246].
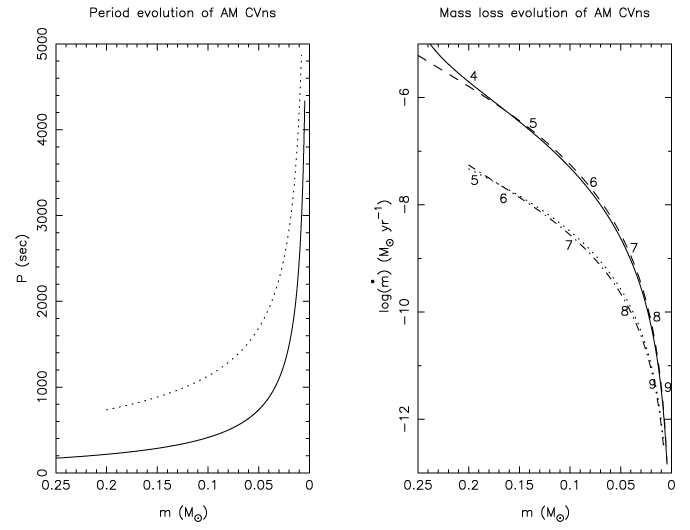
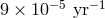 [518*]. The upper dashed line corresponds to
the upper limit for stable mass transfer. The lower solid line is the lower limit for direct accretion.
The upper dash-dot line is the limit set by the Eddington luminosity for stable mass transfer at
a synchronization time limit
[518*]. The upper dashed line corresponds to
the upper limit for stable mass transfer. The lower solid line is the lower limit for direct accretion.
The upper dash-dot line is the limit set by the Eddington luminosity for stable mass transfer at
a synchronization time limit 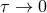 . The lower dash-dot line is the limit set by the Eddington
luminosity for
. The lower dash-dot line is the limit set by the Eddington
luminosity for 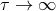 , and the lower broken line is the strict stability limit for the same. The
three dotted lines show how the strict stability limit is raised for shorter synchronization time-scales
ranging from 1000 yr (bottom), 10 yr (center), and 0.1 yr (top). Image reproduced with permission
from Figure 3 of [725], copyright by ASP.
, and the lower broken line is the strict stability limit for the same. The
three dotted lines show how the strict stability limit is raised for shorter synchronization time-scales
ranging from 1000 yr (bottom), 10 yr (center), and 0.1 yr (top). Image reproduced with permission
from Figure 3 of [725], copyright by ASP. Currently, only some of these effects have been studied to a certain extent. In Figure 22*
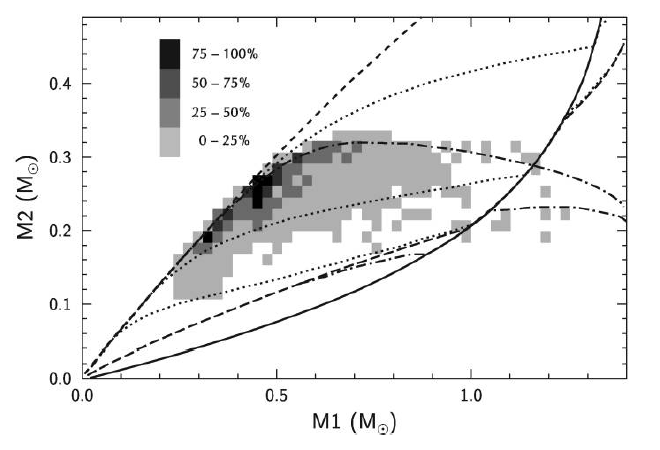
the distribution of birthrates of the possible progenitors of AM CVn stars in the DD channel
from [518*] is over-plotted with constraints imposed by the mass exchange stability conditions, the
Eddington accretion rate, and the efficiency of tidal interaction (in fact, this is the bottom part of
Figure 17* applied to the population of AM CVn stars). It is clear that the substantial number of
AM CVn stars formed via the “double-degenerate” scenario may exist only in the case of efficient
tidal coupling. As shown in [518*], the difference in the expected numbers of stars between
two limiting cases of synchronization time 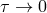 and
and 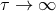 amounts to two orders of
magnitude.
amounts to two orders of
magnitude.
AM CVn systems are so close that in some of them the accretion stream may hit the accretor directly,
and the accretion disk does not form [512*]. The candidate “direct impact” systems currently include the
shortest orbital period known systems HM Cnc (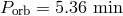 ), V407 Vul (
), V407 Vul (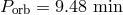 ),
ES Cet (
),
ES Cet (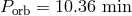 ), see [725] for discussion and references.
), see [725] for discussion and references.
Until quite recently, the evolution of systems with WD donors was calculated using Eq. (70*) and
applying different 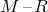 relations for zero-temperature WDs close to
relations for zero-temperature WDs close to 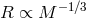 , such as given
in [882, 506, 809*], ignoring detailed models of dwarfs. For He-star donors, radii were approximated by fits
obtained in the evolutionary models of semidetached systems (e.g.,
, such as given
in [882, 506, 809*], ignoring detailed models of dwarfs. For He-star donors, radii were approximated by fits
obtained in the evolutionary models of semidetached systems (e.g., 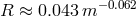 from [776*]). Early
calculations of this kind may be found in [551, 812, 194, 784*, 626, 748, 809*, 790*, 518*, 519*, 661].
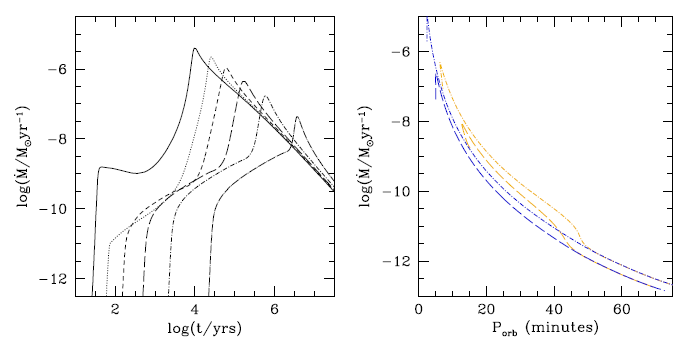
Figure 23* shows examples of the evolution of systems with a helium degenerate donor or a low-mass
“semidegenerate” helium star donor and a carbon-oxygen accretor with initial masses that are currently
thought to be typical for progenitors of AM CVn systems –
from [776*]). Early
calculations of this kind may be found in [551, 812, 194, 784*, 626, 748, 809*, 790*, 518*, 519*, 661].
Figure 23* shows examples of the evolution of systems with a helium degenerate donor or a low-mass
“semidegenerate” helium star donor and a carbon-oxygen accretor with initial masses that are currently
thought to be typical for progenitors of AM CVn systems – 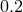 and
and 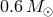 for double degenerates and
for double degenerates and
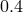 and
and 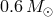 for He-star systems, respectively. In Figure 23* the mass–radius relation [809] is used
for WD, while for the low-mass He-star –
for He-star systems, respectively. In Figure 23* the mass–radius relation [809] is used
for WD, while for the low-mass He-star – 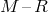 relation from [776]. The same equations are
applied to obtain the model of the population of AM CVn-stars discussed in Sections 10 and
11.
relation from [776]. The same equations are
applied to obtain the model of the population of AM CVn-stars discussed in Sections 10 and
11.
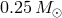 transferring matter to a primary with initial mass of 0.4 and
transferring matter to a primary with initial mass of 0.4 and
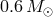 , respectively, assuming efficient coupling between the accretor spin and the orbital motion.
The dash-dotted and dotted lines are for a helium star donor, starting when the helium star becomes
semi-degenerate (with a mass of
, respectively, assuming efficient coupling between the accretor spin and the orbital motion.
The dash-dotted and dotted lines are for a helium star donor, starting when the helium star becomes
semi-degenerate (with a mass of 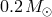 ). Primaries are again
). Primaries are again 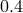 and
and 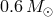 . The numbers
along the lines indicate the logarithm of time in years since the beginning of mass transfer. Image
reproduced with permission from [512*], copyright by ESO.
. The numbers
along the lines indicate the logarithm of time in years since the beginning of mass transfer. Image
reproduced with permission from [512*], copyright by ESO. Equations (25*), (35*), and (70*) imply that for 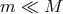 the mass loss rate scales as
the mass loss rate scales as 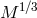 . As a result,
for all combinations of donor and accretor masses, the
. As a result,
for all combinations of donor and accretor masses, the  –
–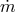 lines form two rather narrow strips within
which they converge with decreasing
lines form two rather narrow strips within
which they converge with decreasing 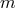 .
.
The “theoretical” model of evolution from shorter periods to longer ones is supported by observations,
which found that the UV luminosity of AM CVn-stars is increasing as the orbital period gets
shorter, since shorter periods are associated with higher 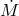 [624]. The orbital period change
[624]. The orbital period change
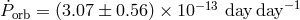 at the
at the 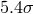 level was quite recently found for the first discovered
eclipsing AM CVn type binary SDSS J0926+3624 (
level was quite recently found for the first discovered
eclipsing AM CVn type binary SDSS J0926+3624 (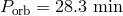 . [746]). This value of
. [746]). This value of 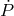 is
consistent with the mass-exchange rate close to
is
consistent with the mass-exchange rate close to 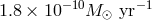 , expected both in the
“double-degenerate” and “helium-star” channels of the evolution of AM CVn stars for the period of
SDSS J0926+3624. Sion et al. [717] estimated accretion rates in several AM CVn binaries by means of
analyses of their far and near-UV spectra and found that in their sample; the system ES Ceti with the
shortest
, expected both in the
“double-degenerate” and “helium-star” channels of the evolution of AM CVn stars for the period of
SDSS J0926+3624. Sion et al. [717] estimated accretion rates in several AM CVn binaries by means of
analyses of their far and near-UV spectra and found that in their sample; the system ES Ceti with the
shortest 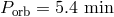 has the highest
has the highest 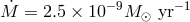 , while the longest orbital period
system GP Com (46.5 min) has the lowest
, while the longest orbital period
system GP Com (46.5 min) has the lowest 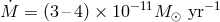 .
.
About 1/3 of AM CVn stars demonstrate outbursts [623*]. The properties of an outburst are well
described by the thermal-viscous disk instability model, see [379] and references therein. Crudely, disks are
unstable for mass accretion rates 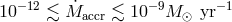 .
.
However, we should note that the time span between the formation of a pair of WDs and their contact
may range from several Myr to several Gyr [790*, 518*]. This means that the approximation of
zero-temperature white dwarfs is not always valid. 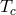 of WD at the onset of mass transfer may be as high
as almost
of WD at the onset of mass transfer may be as high
as almost 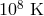 , as estimated by Deloye et al. [142] for WD progenitors of donors of AM CVn stars
from [518*]. This produces differences in period distributions of stars at the onset of mass transfer: while
pairs with zero-temperature WDs have narrow distribution
, as estimated by Deloye et al. [142] for WD progenitors of donors of AM CVn stars
from [518*]. This produces differences in period distributions of stars at the onset of mass transfer: while
pairs with zero-temperature WDs have narrow distribution 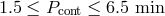 , systems
with finite entropy WDs have
, systems
with finite entropy WDs have 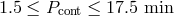 and for about 80% of the model stars
and for about 80% of the model stars
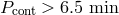 .
.
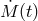 evolution of AM CVn systems with
evolution of AM CVn systems with 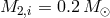 and
and
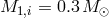 . Systems with donors having the degeneracy parameter
. Systems with donors having the degeneracy parameter 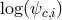 = 3.5, 3.0,
2.5, 2.0, 1.5 and 1.1 are shown by the solid, dotted, short-dashed, dashed, shortdash-dotted and
dash-dotted lines, respectively. Right panel: the dependence of the
= 3.5, 3.0,
2.5, 2.0, 1.5 and 1.1 are shown by the solid, dotted, short-dashed, dashed, shortdash-dotted and
dash-dotted lines, respectively. Right panel: the dependence of the 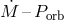 relation on the initial
binary parameters for pairs
relation on the initial
binary parameters for pairs  ,
,  (yellow dashed line),
(yellow dashed line),
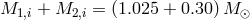 ,
,
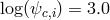 (yellow dot-dashed line),
(yellow dot-dashed line), 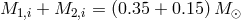 ,
, 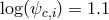 (blue
dashed line),
(blue
dashed line), 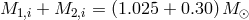 ,
, 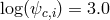 (blue dot-dashed line). Image
reproduced with permission from Figures 6 and 10 of [142], copyright by the authors.
(blue dot-dashed line). Image
reproduced with permission from Figures 6 and 10 of [142], copyright by the authors.Deloye et al. incorporated the pure helium equation of state and the low temperature opacities in their computations of (still unique) series of full evolutionary models of mass-losing donors with different initial mass and electron degeneracy.30 Their main finding is that the evolution of the donor includes three distinct phases: (i) the onset of mass transfer in which the WD contracts, mainly due to the fact that the very outer layers are never degenerate, (ii) the phase of adiabatic expansion, and (iii) the final phase when the thermal time scale of the donor becomes shorter than the mass-loss time scale and the white dwarf cools, contracts, and evolves to a nearly degenerate configuration. Early computations were not able to account for these transitions, since mass-radius relations for zero-temperature WD were used.
In Figure 24* we show, after Deloye et al., 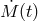 evolution for AM CVn systems with initial masses
evolution for AM CVn systems with initial masses
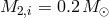 and
and 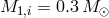 and the dependence of the
and the dependence of the 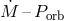 relation on the initial
binary parameters and the degeneracy parameter for pairs with different initial component
masses and electron degeneracy. Note that the initial stage of decreasing
relation on the initial
binary parameters and the degeneracy parameter for pairs with different initial component
masses and electron degeneracy. Note that the initial stage of decreasing 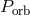 is very short
and hardly observable (however, we do observe HM Cnc). At the final stage of evolution, the
tracks with different initial degeneracy merge. The comparison with Figure 23* shows that the
tracks for the “intermediate” adiabatic mass loss stage based on the zero-temperature
is very short
and hardly observable (however, we do observe HM Cnc). At the final stage of evolution, the
tracks with different initial degeneracy merge. The comparison with Figure 23* shows that the
tracks for the “intermediate” adiabatic mass loss stage based on the zero-temperature 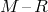 relation and on finite entropy models do not differ significantly, justifying early calculations,
while in the stage of cooling at
relation and on finite entropy models do not differ significantly, justifying early calculations,
while in the stage of cooling at 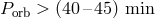 , the mass loss rate becomes so small that
stars will again be hardly observable. The main difference between the approximate and full
computations arises from taking into account the initial non-zero temperature and should be
reflected in
, the mass loss rate becomes so small that
stars will again be hardly observable. The main difference between the approximate and full
computations arises from taking into account the initial non-zero temperature and should be
reflected in 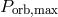 after contact. This may affect the expected GW signal from AM CVn
stars, which must be dominated by the shortest period systems (and the closest ones), see
Section 10.
after contact. This may affect the expected GW signal from AM CVn
stars, which must be dominated by the shortest period systems (and the closest ones), see
Section 10.
Yet another point, which may slightly change the evolution of the double-degenerate family of
AM CVn stars based on the “traditional” 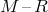 -relation, is the possible presence of a low-mass
(
-relation, is the possible presence of a low-mass
(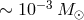 ) but a geometrically thick (several
) but a geometrically thick (several 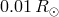 ) nondegenerate layer of hydrogen supported
by
) nondegenerate layer of hydrogen supported
by 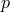 -
-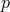 nuclear burning at the surface of the donor at RLOF. Models of mass-transfer in
such systems [131, 337] show that (i) they may make contact at
nuclear burning at the surface of the donor at RLOF. Models of mass-transfer in
such systems [131, 337] show that (i) they may make contact at 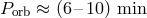 and
(ii) for the first
and
(ii) for the first 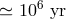 of evolution radii of the donors decrease and systems evolve to
shorter periods, until the H-rich layer is almost shed. This may be the case of AM CVn-type star
HM Cancri (= RX J0806.3+1527), which is also the star with the shortest known
of evolution radii of the donors decrease and systems evolve to
shorter periods, until the H-rich layer is almost shed. This may be the case of AM CVn-type star
HM Cancri (= RX J0806.3+1527), which is also the star with the shortest known
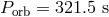 [652] and the only member of the AM CVn class of binaries with a suspected presence of
hydrogen.
[652] and the only member of the AM CVn class of binaries with a suspected presence of
hydrogen.
9.2 “Helium-star family” of AM CVn stars
Precursors of He-star components of AM CVn stars with initial mass 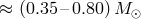 are
are
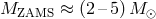 red giants with non-degenerate helium cores (Figure 9*). Helium stars with
red giants with non-degenerate helium cores (Figure 9*). Helium stars with
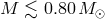 almost do not expand in the course of evolution (by less than 30% [552]). Their lifetimes
are comparable to the main-sequence lifetimes of their precursors (Eq. 68*) and the orbital angular
momentum loss via gravitational waves radiation may bring them to RLOF before the exhaustion of He in
their cores [674, 302, 790]. Mass transfer proceeds steadily if the initial mass ratio of the He
star and the WD is less than approximately 3 [318]. The evolution of low-mass semidetached
systems with He-donors was explored in detail by Yungelson [870]. Referring the reader for
details to this paper, we show in Figure 25* as an example a set of tracks for the system with
initial masses of components
almost do not expand in the course of evolution (by less than 30% [552]). Their lifetimes
are comparable to the main-sequence lifetimes of their precursors (Eq. 68*) and the orbital angular
momentum loss via gravitational waves radiation may bring them to RLOF before the exhaustion of He in
their cores [674, 302, 790]. Mass transfer proceeds steadily if the initial mass ratio of the He
star and the WD is less than approximately 3 [318]. The evolution of low-mass semidetached
systems with He-donors was explored in detail by Yungelson [870]. Referring the reader for
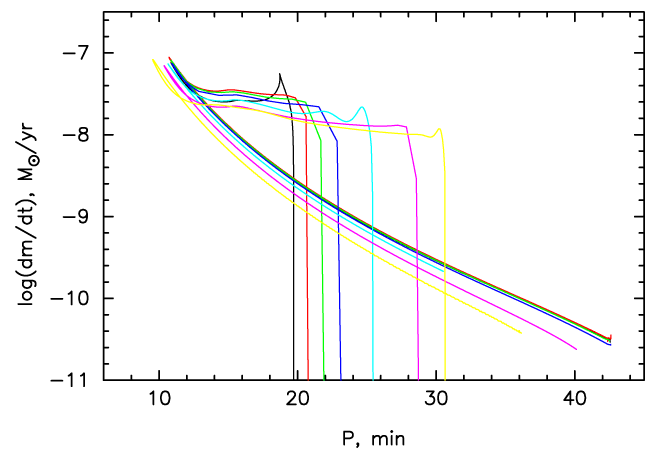
details to this paper, we show in Figure 25* as an example a set of tracks for the system with
initial masses of components 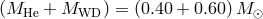 , which have at the formation
(immediately after completion of common envelope evolution) orbital periods from 20 to 130 min.
The initial abundances of He and heavy elements at “He-ZAMS” are assumed to be 0.98 and
0.02, respectively. RLOF in these systems happens at orbital periods of about 20 to 30 min
when He abundance in their cores ranges from 0.98 to 0.066, from the least evolved models
at RLOF to the most evolved ones. The initial stage of increasing Ṁ lasts for
, which have at the formation
(immediately after completion of common envelope evolution) orbital periods from 20 to 130 min.
The initial abundances of He and heavy elements at “He-ZAMS” are assumed to be 0.98 and
0.02, respectively. RLOF in these systems happens at orbital periods of about 20 to 30 min
when He abundance in their cores ranges from 0.98 to 0.066, from the least evolved models
at RLOF to the most evolved ones. The initial stage of increasing Ṁ lasts for 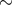 10 Myr
only. The stars reach minimum periods of
10 Myr
only. The stars reach minimum periods of 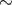 10 min. Their mass at this time is close to
10 min. Their mass at this time is close to
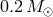 . As shown in [870], the
. As shown in [870], the 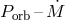 relation very weakly depends on the total mass of the
system. Mass loss leads to the cooling of stellar interiors and quenching of nuclear burning
by the time when the minimum of
relation very weakly depends on the total mass of the
system. Mass loss leads to the cooling of stellar interiors and quenching of nuclear burning
by the time when the minimum of 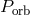 is reached, see Figure 26*. After the minimum of
is reached, see Figure 26*. After the minimum of
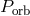 , the chemical composition of the matter transferred to the companion is “frozen” and
does not change during the subsequent evolution. In the course of further evolution the matter
of donors becomes increasingly degenerate, and their mass-ratio relation approaches that of
WD.
, the chemical composition of the matter transferred to the companion is “frozen” and
does not change during the subsequent evolution. In the course of further evolution the matter
of donors becomes increasingly degenerate, and their mass-ratio relation approaches that of
WD.
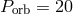 to 130 min. Initial masses of
components are
to 130 min. Initial masses of
components are 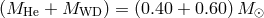 . He abundance in the cores of the donors at
RLOF ranges from 0.98 to 0.066 (left to right). Image from [870], copyright by the author.
. He abundance in the cores of the donors at
RLOF ranges from 0.98 to 0.066 (left to right). Image from [870], copyright by the author.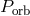 = 15, 20, 25, 30, 35, and
40 min. The initial (post-common-envelope) orbital periods are indicated in the bottom panels. The
sequences differ by the amount of nuclear processing before RLOF. Image reproduced with permission
from Figure 4 of [521], copyright by the authors.
= 15, 20, 25, 30, 35, and
40 min. The initial (post-common-envelope) orbital periods are indicated in the bottom panels. The
sequences differ by the amount of nuclear processing before RLOF. Image reproduced with permission
from Figure 4 of [521], copyright by the authors. As mentioned in Section 7, until recently it was deemed that, at accretion rates of He onto a WD below
several units of 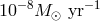 ,
, 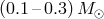 of He accumulates at the WD surface and then detonates;
converging detonation waves propagate to the center of the accretor and ignite carbon detonation close to
the center. Prior to the minimum
of He accumulates at the WD surface and then detonates;
converging detonation waves propagate to the center of the accretor and ignite carbon detonation close to
the center. Prior to the minimum  He-donors provide
He-donors provide 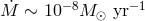 . Correspondingly,
Nelemans et al. [518*, 519*] considered “optimistic” and “pessimistic” scenarios for the formation of
AM CVn stars in the He channel, depending on the amount of He that may accrete, detonate and destroy
the AM CVn star precursor:
. Correspondingly,
Nelemans et al. [518*, 519*] considered “optimistic” and “pessimistic” scenarios for the formation of
AM CVn stars in the He channel, depending on the amount of He that may accrete, detonate and destroy
the AM CVn star precursor: 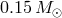 or
or 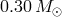 . The difference in the predicted number of
observed systems reached factor
. The difference in the predicted number of
observed systems reached factor 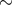 2 in favor of the first scenario. However, a comparison of the
accretion and mass loss rates in Figures 25* and 14* suggests that the donors instead experience
strong flashes of He-burning than detonations, and the model space density of AM CVn stars
in [518*, 519*] is, most probably, an underestimate. This exacerbates the known problem of a
possibly-almost factor
2 in favor of the first scenario. However, a comparison of the
accretion and mass loss rates in Figures 25* and 14* suggests that the donors instead experience
strong flashes of He-burning than detonations, and the model space density of AM CVn stars
in [518*, 519*] is, most probably, an underestimate. This exacerbates the known problem of a
possibly-almost factor 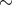 50 deficit of the observed AM CVn star spatial density compared to
theoretical predictions [651, 90*]. However, as noted in [90], the “observational” estimate of the
number of AM CVn stars depends on the assumed intrinsic distribution of their magnitudes, and
uncertainty in this distribution may also contribute to the mismatch of theoretical expectations and
observations.
50 deficit of the observed AM CVn star spatial density compared to
theoretical predictions [651, 90*]. However, as noted in [90], the “observational” estimate of the
number of AM CVn stars depends on the assumed intrinsic distribution of their magnitudes, and
uncertainty in this distribution may also contribute to the mismatch of theoretical expectations and
observations.
An accurate knowledge of the formation channels and the space density of interacting double-degenerates is necessary for a better understanding of the stability of mass exchange, processes in common envelopes and proper modeling of the gravitational wave foreground (Section 10). The same is true for ultra-compact X-ray sources.
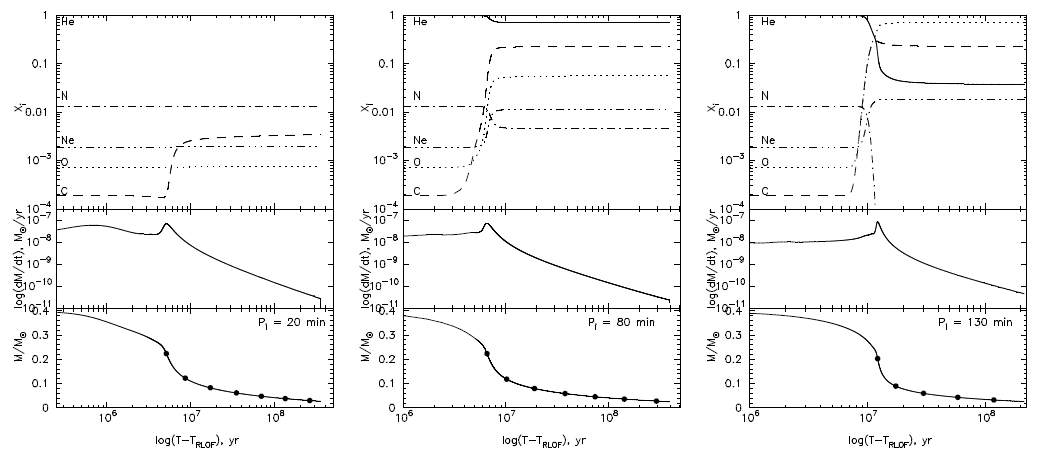
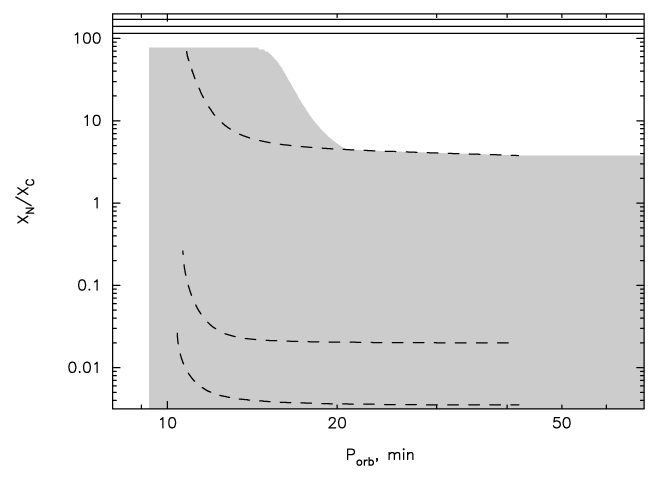
The chemical composition of IDD may reveal their origins [515, 521]. In the double degenerate channel,
the matter transferred is a product of low-temperature CNO-burning, and the abundances of He,
C, N, and O depend on the WD progenitor’s mass. In the He-star channel, the abundances
depend on the initial mass of the donor and the extent of He-depletion by the time of RLOF
(Figure 26*). In the “evolved CV-channel”, the matter may also contain the traces of hydrogen.
As concerns UCXB, it was shown in [877*] that the initial masses of their donors are limited
from above by 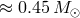 . This means that some of the donors may descend from “hybrid”
WDs. However, the latter lose their He-rich envelopes at very early phases of mass exchange,
and, since they are descendants of helium stars, the matter transferred by them should not
contain He. Nelemans et al. [521] constructed a set of diagnostic diagrams with abundance ratios
(in mass)
. This means that some of the donors may descend from “hybrid”
WDs. However, the latter lose their He-rich envelopes at very early phases of mass exchange,
and, since they are descendants of helium stars, the matter transferred by them should not
contain He. Nelemans et al. [521] constructed a set of diagnostic diagrams with abundance ratios
(in mass) 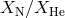 ,
, 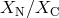 ,
, 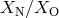 ,
, 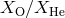 ,
, 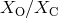 as functions of
as functions of 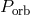 for
different groups of donors. As an example, we show in Figure 27* such a diagram for the ratio
for
different groups of donors. As an example, we show in Figure 27* such a diagram for the ratio
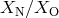 .
.
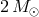 stars (top to bottom). Image reproduced with permission from Figure 11 of [521],
copyright by the authors.
stars (top to bottom). Image reproduced with permission from Figure 11 of [521],
copyright by the authors.The above-described diagnostic of abundances in the spectra of known IDD and other means of analysis suggest that HM Cnc, CP Eri, GP Com, V396 Hya, SDSS J124058.03–015919.2, SDSS J080449.49+161624.8 almost definitely belong to the WD-family, while AM CVn, HP Lib, CR Boo, V803 Cen, SDSS J173047.59+554518.5 may have helium-star donors [521, 725, 88]. Significantly-evolved He-star donors are ruled out for SDSS J113732.32+405458.3 and SDSS J150551.58+065948.7 [91].
Among the UCXBs there are two systems (4U 1626-67 and 4U 0614+09) in which detection of C and O lines but no He lines suggests hybrid white dwarf or very evolved helium star donors. For 4U 1916-05, the detected He and N lines suggest a He white dwarf or an unevolved helium star donor [521]. For the rest, data are not sufficient for classification.
9.3 Final stages of evolution of interacting double-degenerate systems
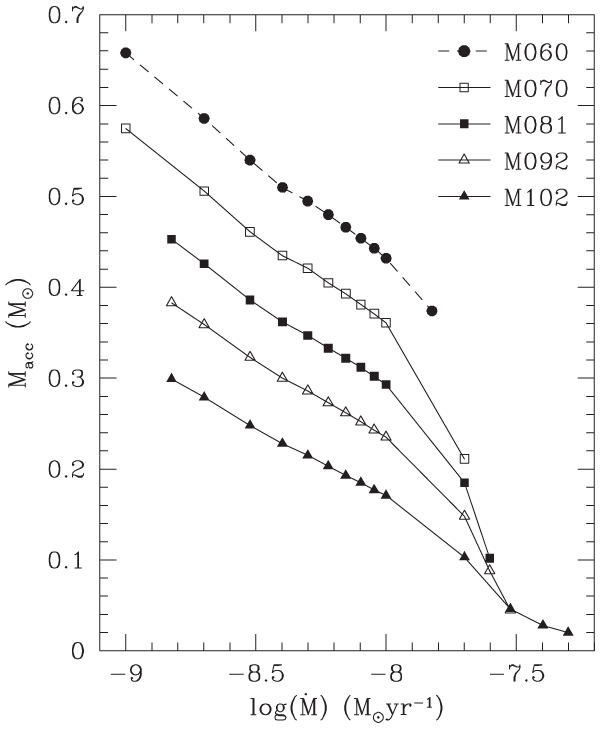
By means of population synthesis modeling, Solheim and Yungelson [727] found that accumulation of
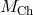 by WD in the double-degenerate channel of formation and evolution of IDD is possible at a rate of
by WD in the double-degenerate channel of formation and evolution of IDD is possible at a rate of
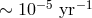 , while Ruiter et al. [662] provided an estimate that is an order of magnitude higher. Note
that in both studies SN Ia require massive WD accretors, which are not typical for observed
IDD.
, while Ruiter et al. [662] provided an estimate that is an order of magnitude higher. Note
that in both studies SN Ia require massive WD accretors, which are not typical for observed
IDD.
Yet another kind of explosive event may characterize the evolution of IDD [48, 697, 702] – faint thermonuclear supernovae dubbed SN .Ia.
As described above, in the WD-family of AM CVn stars, the mass transfer rate initially is as high as
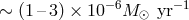 and decreases at later times. While during the initial phase of accretion the
nuclear burning in the accreted He envelope of the WD is thermally stable, it becomes thermally unstable
as
and decreases at later times. While during the initial phase of accretion the
nuclear burning in the accreted He envelope of the WD is thermally stable, it becomes thermally unstable
as 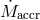 drops (Figure 14*). In the He-star family, the mass transfer rate before reaching the orbital
period minimum is several
drops (Figure 14*). In the He-star family, the mass transfer rate before reaching the orbital
period minimum is several 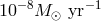 , i.e., accretors are in the strong He-flashes regime ab ovo. The
“ignition” mass for He-outbursts increases with decreasing
, i.e., accretors are in the strong He-flashes regime ab ovo. The
“ignition” mass for He-outbursts increases with decreasing 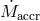 . This yields
. This yields 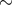 10 He-flashes
in the
10 He-flashes
in the 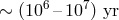 before the amount of accreted mass required to achieve He-ignition
before the amount of accreted mass required to achieve He-ignition
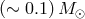 becomes larger than the mass of the donor (Figure 28*), while de facto the binaries
are already in the “detonation” regime of He-burning (Figure 14*). Thus, there must be the
“last” most powerful outburst with an ignition mass of
becomes larger than the mass of the donor (Figure 28*), while de facto the binaries
are already in the “detonation” regime of He-burning (Figure 14*). Thus, there must be the
“last” most powerful outburst with an ignition mass of 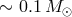 which can occur in the
hydrodynamic regime. It can lead to He-detonation, which can be potentially observable as
a faint thermonuclear supernova [48]. Since the mass transfer rate drops very rapidly after
RLOF, it is plausible that the observed AM CVn stars already experienced their last strong
He-flash (which could be of the SN .Ia scale) and are now slowly transferring He without any
expected nuclear-powered phenomena. Supernovae .Ia probably do not initiate detonations of
low-mass accretors of AM CVn stars since the masses of the exploding shells are insufficient for
this [713, 698].
which can occur in the
hydrodynamic regime. It can lead to He-detonation, which can be potentially observable as
a faint thermonuclear supernova [48]. Since the mass transfer rate drops very rapidly after
RLOF, it is plausible that the observed AM CVn stars already experienced their last strong
He-flash (which could be of the SN .Ia scale) and are now slowly transferring He without any
expected nuclear-powered phenomena. Supernovae .Ia probably do not initiate detonations of
low-mass accretors of AM CVn stars since the masses of the exploding shells are insufficient for
this [713, 698].
As estimated in [48], SN .Ia may happen every 5000 to 15 000 yr in an E/S0 galaxy. Their brightness
and duration are about 1/10 of the ordinary SN Ia event. The rise times of the light curves in all
bands are very rapid ( 10 days). The explosion nucleosynthesis in these events primarily
yields heavy
10 days). The explosion nucleosynthesis in these events primarily
yields heavy  -chain elements (40Ca through 56Ni) and unburned He (up to 80%) [702, 493].
It is interesting that with the 1-day dynamic-cadence experiment on the Palomar Transient
Factory,31
it is expected to annually discover a few such events.
-chain elements (40Ca through 56Ni) and unburned He (up to 80%) [702, 493].
It is interesting that with the 1-day dynamic-cadence experiment on the Palomar Transient
Factory,31
it is expected to annually discover a few such events.
SN 2010X (PTF 10bhp) with extremely rapid decay (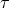 =5 day) was, for instance,
suggested as a candidate SN .Ia [344]. Another candidate may be a faint type Ib supernova,
SN 2005E, in the halo of the nearby isolated galaxy, NGC 1032. Spectroscopic observations and
analysis reveal high velocities of the ejecta, dominated by helium-burning products including a large amount
of radioactive 44Ti, just as expected for SN .Ia. However, as noticed by Drout et al. [165], e.g., severely
stripped-envelope SN Ic explosions may mimic SNe .Ia.
=5 day) was, for instance,
suggested as a candidate SN .Ia [344]. Another candidate may be a faint type Ib supernova,
SN 2005E, in the halo of the nearby isolated galaxy, NGC 1032. Spectroscopic observations and
analysis reveal high velocities of the ejecta, dominated by helium-burning products including a large amount
of radioactive 44Ti, just as expected for SN .Ia. However, as noticed by Drout et al. [165], e.g., severely
stripped-envelope SN Ic explosions may mimic SNe .Ia.
It is possible that strong flashes of He-burning can be identified with He-novae, like H-outbursts are
identified with classical novae. The sole known object that may be a prototype of He-novae –
V445 Pup erupted in 2000, and its optical and IR spectra are hydrogen-deficient [15, 853].
Provisional 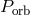 of V445 Pup is
of V445 Pup is 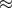 0.65 day [247]. Several other candidate He-novae have
been suggested, but remain still unexplored [657]. The estimated pre-outburst luminosity of
V445 Pup is
0.65 day [247]. Several other candidate He-novae have
been suggested, but remain still unexplored [657]. The estimated pre-outburst luminosity of
V445 Pup is 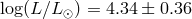 [854]. Apparently, it is associated with a more massive
system than the typical AM CVn star, but one cannot exclude nova-scale events among AM
CVn’s.
[854]. Apparently, it is associated with a more massive
system than the typical AM CVn star, but one cannot exclude nova-scale events among AM
CVn’s.

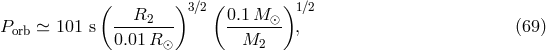
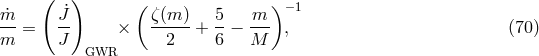

 .
Piersanti, Tornambé and Yungelson
.
Piersanti, Tornambé and Yungelson