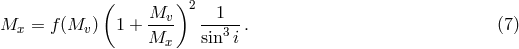2 Observations of Double Compact Stars
2.1 Compact binaries with neutron stars
NS binaries have been discovered when one of their components is observed as a radio pulsar [292*]. The precise pulsar timing allows one to search for a periodic variation due to the binary motion. This technique is reviewed in detail by Lorimer [444]; applications of pulsar timing for general relativity tests are reviewed by Stairs [733]. Techniques and results of measurements of NS mass and radii in different types of binaries are summarized by Lattimer [411].
Basically, pulsar timing provides the following Keplerian orbital parameters of the binary system: the
binary orbital period 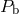 as measured from periodic Doppler variations of the pulsar spin, the projected
semi-major axis
as measured from periodic Doppler variations of the pulsar spin, the projected
semi-major axis 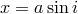 as measured from the semi-amplitude of the pulsar radial velocity curve (
as measured from the semi-amplitude of the pulsar radial velocity curve ( is
the binary inclination angle defined such that
is
the binary inclination angle defined such that 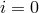 for face-on systems), the orbital eccentricity
for face-on systems), the orbital eccentricity  as
measured from the shape of the pulsar radial velocity curve, and the longitude of periastron
as
measured from the shape of the pulsar radial velocity curve, and the longitude of periastron 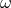 at a
particular epoch
at a
particular epoch 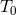 . The first two parameters allow one to construct the mass function of the secondary
companion,
. The first two parameters allow one to construct the mass function of the secondary
companion,
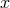 is measured in light-seconds,
is measured in light-seconds, 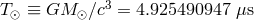 , and
, and  and
and
 denote masses of the pulsar and its companion, respectively. This function gives the strict
lower limit on the mass of the unseen companion. However, assuming the pulsar mass to have
the typical value of a NS mass (for example, confined between the lowest measured NS mass
denote masses of the pulsar and its companion, respectively. This function gives the strict
lower limit on the mass of the unseen companion. However, assuming the pulsar mass to have
the typical value of a NS mass (for example, confined between the lowest measured NS mass
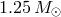 for PSR J0737–3039B [451*] and the maximum measured NS
mass of
for PSR J0737–3039B [451*] and the maximum measured NS
mass of 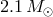 in the NS–WD binary PSR J0751+1807 [527]), one can
estimate the mass of the secondary star even without knowing the binary inclination angle
in the NS–WD binary PSR J0751+1807 [527]), one can
estimate the mass of the secondary star even without knowing the binary inclination angle
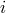 .
.
Long-term pulsar timing allows measurements of several relativistic phenomena: the advance of
periastron 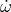 , the redshift parameter
, the redshift parameter 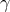 , the Shapiro delay within the binary system qualified through
post-Keplerian parameters
, the Shapiro delay within the binary system qualified through
post-Keplerian parameters  ,
,  , and the binary orbit decay
, and the binary orbit decay 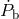 . From the post-Keplerian parameters
the individual masses
. From the post-Keplerian parameters
the individual masses 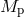 ,
, 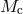 and the binary inclination angle
and the binary inclination angle 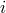 can be calculated [74].
can be calculated [74].
Of the post-Keplerian parameters of pulsar binaries, the periastron advance rate is usually measured most readily. Assuming it to be entirely due to general relativity, the total mass of the system can be evaluated:
The high value of the derived total mass of a system (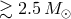 ) suggests the presence of another NS or even a
BH.11
) suggests the presence of another NS or even a
BH.11
If the masses of components, binary period, and eccentricity of a compact binary system are known, it is easy to calculate the time it takes for the binary companions to coalesce due to GW emission using the quadrupole formula for GW emission [579*] (see Section 3.1.4 for more detail):
Here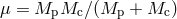 is the reduced mass of the binary. Some observed and derived parameters of
known compact binaries with NSs are collected in Tables 2 and 3.
is the reduced mass of the binary. Some observed and derived parameters of
known compact binaries with NSs are collected in Tables 2 and 3.
| PSR | 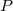 |
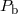 |
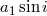 |
 |
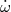 |
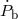 |
Ref. |
| [ms] | [d] | [lt-s] | [deg yr–1] | [× 10–12] | |||
| J0737–3039A | 22.70 | 0.102 | 1.42 | 0.088 | 16.88 | –1.24 | [77*] |
| J0737–3039B | 2773 | — | — | — | — | — | [451] |
| J1518+4904 | 40.93 | 8.634 | 20.04 | 0.249 | 0.011 | ? | [526] |
| B1534+12 | 37.90 | 0.421 | 3.73 | 0.274 | 1.756 | –0.138 | [844, 735] |
| J1756–2251 | 28.46 | 0.320 | 2.75 | 0.181 | 2.585 | ? | [193] |
| J1811–1736 | 104.18 | 18.779 | 34.78 | 0.828 | 0.009 | < 30 | [450] |
| J1829+2456 | 41.00 | 1.176 | 7.236 | 0.139 | 0.28 | ? | [96] |
| J1906+0746 | 144.07 | 0.116 | 1.42 | 0.085 | 7.57 | ? | [445] |
| B1913+16 | 59.03 | 0.323 | 2.34 | 0.617 | 4.227 | –2.428 | [292*] |
| B2127+11C | 30.53 | 0.335 | 2.52 | 0.681 | 4.457 | –3.937 | [12, 615] |
| PSR | 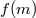 |
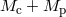 |
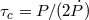 |
 |
[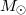 ] ] |
[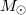 ] ] |
[Myr] | [Myr] | |
| J0737–3039A | 0.29 | 2.58 | 210 | 87 |
| J0737–3039B | — | — | 50 | — |
| J1518+4904 | 0.12 | 2.62 | 9.6 × 106 | |
| B1534+12 | 0.31 | 2.75 | 248 | 2690 |
| J1756–2251 | 0.22 | 2.57 | 444 | 1690 |
| J1811–1736 | 0.13 | 2.6 | 1.7 × 106 | |
| J1829+2456 | 0.29 | 2.53 | 60 × 103 | |
| J1906+0746 | 0.11 | 2.61 | 0.112 | 300 |
| B1913+16 | 0.13 | 2.83 | 108 | 310 |
| B2127+11C | 0.15 | 2.71 | 969 | 220 |
2.2 How frequent are NS binary coalescences?
As is seen in Table 3, only six NS binary systems presently known will merge over a time interval shorter than
 10 Gyr: J0737–3039A, B1534+12, J1756–2251,
J1906+0746, B1913+16, and B2127+11C. Of these six
systems, one (PSR B2127+11C) is located in the globular cluster M15. This system
may have a different formation history, so usually it is not included in the analysis of the coalescence
rate of Galactic compact binaries. The formation and evolution of relativistic binaries in dense
stellar systems is reviewed elsewhere [39*]. For a general review of pulsars in globular clusters see
also [82].
10 Gyr: J0737–3039A, B1534+12, J1756–2251,
J1906+0746, B1913+16, and B2127+11C. Of these six
systems, one (PSR B2127+11C) is located in the globular cluster M15. This system
may have a different formation history, so usually it is not included in the analysis of the coalescence
rate of Galactic compact binaries. The formation and evolution of relativistic binaries in dense
stellar systems is reviewed elsewhere [39*]. For a general review of pulsars in globular clusters see
also [82].
Let us try to estimate the NS-binary merger rate from pulsar binary statistics, which is free from many
uncertainties of stellar evolution. Usually, the estimate is based on the following extrapolation [505, 586*].
Suppose, we observe 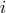 classes of Galactic pulsar binaries. Taking into account various selection effects of
pulsar surveys (see, e.g., [504, 361*]), the Galactic number of pulsars
classes of Galactic pulsar binaries. Taking into account various selection effects of
pulsar surveys (see, e.g., [504, 361*]), the Galactic number of pulsars 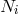 in each class can be evaluated. To
compute the Galactic merger rate of NS binaries, we need to know the time since the birth of the NS
observed as a pulsar in the given binary system. This time is the sum of the observed characteristic
pulsar age
in each class can be evaluated. To
compute the Galactic merger rate of NS binaries, we need to know the time since the birth of the NS
observed as a pulsar in the given binary system. This time is the sum of the observed characteristic
pulsar age 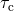 and the time required for the binary system to merge due to GW orbit decay
and the time required for the binary system to merge due to GW orbit decay
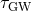 . With the exception of PSR J0737–3039B and the recently discovered
PSR J1906+0746, pulsars that we observe in NS binary systems are old recycled pulsars
that were spun-up by accretion from the secondary companion to the period of several tens of ms (see
Table 2). Thus, their characteristic ages can be estimated as the time since termination of spin-up
by accretion (for the younger pulsar PSR J0737–3039B this time can also
be computed as the dynamical age of the pulsar,
. With the exception of PSR J0737–3039B and the recently discovered
PSR J1906+0746, pulsars that we observe in NS binary systems are old recycled pulsars
that were spun-up by accretion from the secondary companion to the period of several tens of ms (see
Table 2). Thus, their characteristic ages can be estimated as the time since termination of spin-up
by accretion (for the younger pulsar PSR J0737–3039B this time can also
be computed as the dynamical age of the pulsar, 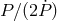 , which gives essentially the same
result).
, which gives essentially the same
result).
Then the merger rate  can be calculated as
can be calculated as  (summed over all pulsar
binaries). The detailed analysis [361] indicates that the Galactic merger rate of NS binaries is mostly
determined by pulsars with faint radio luminosity and short orbital periods. Presently, it is the nearby
(600 pc) pulsar-binary system PSR J0737–3039 with a short orbital period of 2.4 hr [77*]
that mostly determines the empirical estimate of the merger rate. According to Kim et al. [362], “the most
likely values of DNS merger rate lie in the range 3 – 190 per Myr depending on different pulsar models”.
This estimate has recently been revised in [363*] based on the analysis of binary pulsars in the
Galactic disk: PSR 1913+16, PSR 1534+12, and pulsar binary
PSR J0737–3039A and J0737–3039B, giving the Galactic NS + NS
coalescence rate
(summed over all pulsar
binaries). The detailed analysis [361] indicates that the Galactic merger rate of NS binaries is mostly
determined by pulsars with faint radio luminosity and short orbital periods. Presently, it is the nearby
(600 pc) pulsar-binary system PSR J0737–3039 with a short orbital period of 2.4 hr [77*]
that mostly determines the empirical estimate of the merger rate. According to Kim et al. [362], “the most
likely values of DNS merger rate lie in the range 3 – 190 per Myr depending on different pulsar models”.
This estimate has recently been revised in [363*] based on the analysis of binary pulsars in the
Galactic disk: PSR 1913+16, PSR 1534+12, and pulsar binary
PSR J0737–3039A and J0737–3039B, giving the Galactic NS + NS
coalescence rate 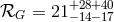 per Myr (95% and 90% confidence level, respectively). The estimates by
population synthesis codes are still plagued by uncertainties in the statistics of binaries, in modeling
binary evolution and supernovae. The most optimistic “theoretical” predictions amount to
per Myr (95% and 90% confidence level, respectively). The estimates by
population synthesis codes are still plagued by uncertainties in the statistics of binaries, in modeling
binary evolution and supernovae. The most optimistic “theoretical” predictions amount to
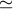 300 Myr–1 [788*, 34*, 157*].
300 Myr–1 [788*, 34*, 157*].
An independent estimate of the NS-binary merger rate can also be obtained using another astrophysical
argument, originally suggested by Bailes [20]. 1) Take the formation rate of single pulsars in the Galaxy
 (e.g., [190]; see also the discussion on the NS formation rate of different types
in [351*]), which appears to be correct to within a factor of two. 2) Take the fraction of NS binary systems
in which one component is a normal (not recycled) pulsar and which are close enough to merge within the
Hubble time,
(e.g., [190]; see also the discussion on the NS formation rate of different types
in [351*]), which appears to be correct to within a factor of two. 2) Take the fraction of NS binary systems
in which one component is a normal (not recycled) pulsar and which are close enough to merge within the
Hubble time, 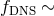 (a few)
(a few) 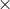 1/2000). Assuming a steady state, this fraction yields the formation
rate of coalescing NS binaries in the Galaxy
1/2000). Assuming a steady state, this fraction yields the formation
rate of coalescing NS binaries in the Galaxy  (a few 10s)× Myr–1, in good
correspondence with other empirical estimates [363*]. Clearly, the Bailes limit ignores the fact that the NS
formation rate can actually be higher than the pulsar formation rate [351] and possible selection effects
related to the evolution of stars in binary systems, but the agreement with other estimates seems to be
encouraging.
(a few 10s)× Myr–1, in good
correspondence with other empirical estimates [363*]. Clearly, the Bailes limit ignores the fact that the NS
formation rate can actually be higher than the pulsar formation rate [351] and possible selection effects
related to the evolution of stars in binary systems, but the agreement with other estimates seems to be
encouraging.
Extrapolation beyond the Galaxy is usually done by scaling the Galactic merger rate to the
volume over which the merger events can be detected for a given GW detector’s sensitivity.
The scaling factor widely used is the ratio between the B-band luminosity density in the local
Universe, correlating with the star-formation rate (SFR), and the B-band luminosity of the
galaxy [586, 333, 376*]. For this purpose one can also use the direct ratio of the galactic star formation rate
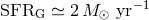 [108, 353, 537] to the (dust-corrected) star formation rate in the local Universe
[108, 353, 537] to the (dust-corrected) star formation rate in the local Universe
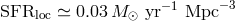 [577, 682]. These estimates yield the (Euclidean) relation
[577, 682]. These estimates yield the (Euclidean) relation
Bear in mind that since NS-binary coalescences can be strongly delayed compared to star formation, the
estimate of their rate in the nearby Universe based on present-day star formation density may be
underevaluated. Additionally, these estimates inevitably suffer from many other astrophysical uncertainties.
For example, a careful study of local SFR from analysis of an almost complete sample of nearby galaxies
within 11 Mpc using different SFR indicators and supernova rate measurements during 13 years of
observations [63*] results in the local SFR density 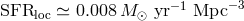 . However, Horiuchi
et al. [288] argue that estimates of the local SFR can be strongly affected by stellar rotation. Using new
stellar evolutionary tracks [173], they derived the local SFR density
. However, Horiuchi
et al. [288] argue that estimates of the local SFR can be strongly affected by stellar rotation. Using new
stellar evolutionary tracks [173], they derived the local SFR density 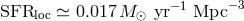 and
noted that the estimate of the local SFR from core-collapse supernova counts is higher by a factor of
2 – 3.
and
noted that the estimate of the local SFR from core-collapse supernova counts is higher by a factor of
2 – 3.
Therefore, the actual value of the scaling factor from the galactic merger rate is presently uncertain to
within a factor of at least two. The mean SFR density steeply increases with distance (e.g., as
 [127]) and can be higher in individual galaxies. Thus, for the conservative
galactic NS + NS merger rate
[127]) and can be higher in individual galaxies. Thus, for the conservative
galactic NS + NS merger rate 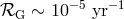 using scaling relation (5*) we obtain a few
NS-binary coalescences per year of observations within the assumed advanced GW detectors horizon
using scaling relation (5*) we obtain a few
NS-binary coalescences per year of observations within the assumed advanced GW detectors horizon
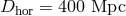 .
.
However, one should differentiate between the possible merging rate within some volume
and the detection rate of certain types of compact binaries from this volume (see Section 6
below and [2*] for more detail) – the detection rate by one detector can be lower by a factor of
 . The correction factor takes into account the averaging over all sky locations and
orientations.
. The correction factor takes into account the averaging over all sky locations and
orientations.
The latest results of the search for GWs from coalescing binary systems within 40 Mpc
volume using LIGO and Virgo observations between July 7, 2009, and October 20, 2010 [3*]
established an observational upper limit to the 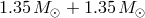 NS binary coalescence rate of
NS binary coalescence rate of
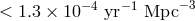 . Adopting the scaling factor from the measured local SFR density [63], the
corresponding galactic upper limit is
. Adopting the scaling factor from the measured local SFR density [63], the
corresponding galactic upper limit is 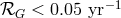 . This is still too high to put interesting
astrophysical bounds, but even upper limits from the advanced LIGO detector are expected to be very
constraining.
. This is still too high to put interesting
astrophysical bounds, but even upper limits from the advanced LIGO detector are expected to be very
constraining.
2.3 Black holes in binary systems
Black holes (BH) in binary systems remain on the top of astrophysical studies. Most of the experimental knowledge on BH physics has so far been obtained through electromagnetic channels (see [618] for a review), but the fundamental features of BHs will be studied through GW experiments [673*]. Stellar-mass black holes result from gravitational collapse of the cores of the most massive stars [851] (see [216] for the recent progress in the physics of gravitational collapse).
Stellar-mass BHs can be observed in close binary systems at the stage of mass accretion from the secondary companion as bright X-ray sources [690]. X-ray studies of BHs in binary systems (which are usually referred to as ‘Black Hole Candidates’, BHC) are reviewed in [633*]. There is strong observational evidence of the launch of relativistic jets from the inner parts of accretion disks in BHC, which can be observed in the range from radio to gamma-rays (the ‘galactic microquasar’ phenomenon, [486, 197, 756]).
Optical spectroscopy and X-ray observations of BHC allow measurements of masses and, under certain
assumptions, spins of BHs [476]. The measured mass distribution of stellar mass BHs is centered on
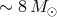 and appears to be separated from NS masses [550] by a gap (the absence of compact star masses
in the
and appears to be separated from NS masses [550] by a gap (the absence of compact star masses
in the 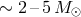 range) [22, 100, 549, 189, 580] (see, however, the discussion of possible systematic
errors leading to overestimation of dynamical BH masses in X-ray transients in [386]). The mass gap, if
real, can be indicative of the supernova-explosion–mechanism details (see, for example, [610, 37, 213]). It is
also possible that the gap is due to “failed core-collapse supernovae” from red supergiants with masses
range) [22, 100, 549, 189, 580] (see, however, the discussion of possible systematic
errors leading to overestimation of dynamical BH masses in X-ray transients in [386]). The mass gap, if
real, can be indicative of the supernova-explosion–mechanism details (see, for example, [610, 37, 213]). It is
also possible that the gap is due to “failed core-collapse supernovae” from red supergiants with masses
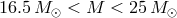 , which would produce black holes with a mass equal to the mass of the helium
core (
, which would produce black holes with a mass equal to the mass of the helium
core (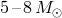 ) before the collapse, as suggested by Kochanek [371*]. Adopting the latter hypothesis would
increase by
) before the collapse, as suggested by Kochanek [371*]. Adopting the latter hypothesis would
increase by 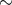 20% the stellar-mass BH formation rate. However, it is unclear how binary
interaction can change the latter possibility. We stress here once again that this important
issue remains highly uncertain due to the lack of “first-principles” calculations of stellar-core
collapses.
20% the stellar-mass BH formation rate. However, it is unclear how binary
interaction can change the latter possibility. We stress here once again that this important
issue remains highly uncertain due to the lack of “first-principles” calculations of stellar-core
collapses.
Most of more than 20 galactic BHC appear as X-ray transients with a rich phenomenology of outbursts and spectral/time variability [633*], and only a few (Cyg X-1, LMC X-3, LMC X-1 and SS 433) are persistent X-ray sources. Optical companions in BH transients are low-mass stars (main-sequence or evolved) filling Roche lobes, and the transient activity is apparently related to accretion-disk instability [409*]. Their evolution is driven by orbital angular momentum loss due to GW emission and magnetic stellar wind [619]. Persistent BHC, in contrast, have early-type massive optical companions and belong to the class of High-Mass X-ray Binaries (HMXB) (see [755*, 797] and references therein).
Like in the case of pulsar timing for NSs, to estimate the mass of the BH companion in a
close binary system one should measure the radial velocity curve of the companion (usually
optical) star from spectroscopic observations. The radial velocity curve (i.e., the dependence
of the radial velocity of the companion on the binary phase) has a form that depends on the
orbital eccentricity  , and the amplitude
, and the amplitude 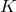 . In the Newtonian limit for two point masses,
the binary mass function can be expressed through the observed quantities
. In the Newtonian limit for two point masses,
the binary mass function can be expressed through the observed quantities 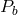 (the binary
orbital period), orbital eccentricity
(the binary
orbital period), orbital eccentricity  and semi-amplitude of the radial velocity curve
and semi-amplitude of the radial velocity curve  as
as
 and orbital inclination angle
and orbital inclination angle 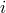 are known from independent
measurements (for example, from the analysis of optical light curve and the duration of X-ray eclipse), the
mass function of the optical component gives the lower limit of the BH mass:
are known from independent
measurements (for example, from the analysis of optical light curve and the duration of X-ray eclipse), the
mass function of the optical component gives the lower limit of the BH mass: 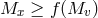 .
.
When using the optical mass function to estimate the BH mass as described above, one should always check the validity of approximations used in deriving Eq. (6*) (see a detailed discussion of different effects related to the non-point-like shape of the optical companion in, e.g., [99]). For example, the optical O-B or Wolf–Rayet (WR) stars in HMXBs have a powerful high-velocity stellar wind, which can affect the dynamical BH-mass estimate based on spectroscopic measurements (see the discussion in [452] for BH + WR binaries).
Parameters of known Galactic and extragalactic HMXB with black holes are summarized in Table 4.
No PSR + BH system has been observed so far, despite optimistic expectations from the early population synthesis calculations [431*] and recent examination of the possible dynamical formation of such a binary in the Galactic center [191]. Therefore, it is not possible to obtain direct experimental constraints on the NS + BH coalescence rate based on observations of real systems. Recently, the BH candidate with Be-star MWC 656 in a wide 60-day orbit was reported [93] (see Table 4). It is a very weak X-ray source [498], but can be the counterpart of the gamma-ray source AGL J2241+4454. The BH mass estimation in this case depends on the spectral classification and mass of the Be star. This system can be the progenitor of the long-sought BH + NS binary. Whether or not this binary system can become a merging BH + NS binary depends on the details of the common envelope phase, which is thought to happen after the bright accretion stage in this system, when the Be-star will evolve to the giant stage.
| Source |  (hr) (hr) |
 [ [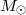 ] ] |
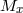 [ [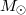 ] ] |
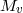 [ [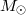 ] ] |
Sp. type | Ref. |
|
Galactic binaries
|
||||||
| Cyg X-1 | 134.4 | 0.244 |  15 15 |
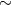 19 19 |
O9.7Iab | [543] |
| SS 433 | 313.9 | 0.268 | 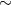 5 5 |
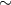 18 18 |
A7I: | [101*] |
| Cyg X-3 | 4.8 | 0.027 | 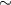 2.4 2.4 |
 10 10 |
WN | [883] |
| MWC 656 | 1448.9 | 0.205 | 3.8 – 6.9 | 10 – 16 | B1.5–B2 IIIe | [93] |
|
Extragalactic binaries
|
||||||
| LMC X-1 | 93.8 | 0.13 | 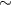 11 11 |
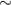 32 32 |
O7III | [545] |
| M33 X-7 | 82.8 | 0.46 |  16 16 |
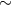 70 70 |
O7-8III | [544] |
| IC10 X-1 | 34.4 | 7.64 |  23 – 33 23 – 33 |
 17 – 35 17 – 35 |
WR | [611, 710] |
| NGC 300 X-1 | 32.3 | 2.6 | 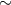 14.5 14.5 |
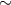 15 15 |
WR | [124*] |
|
Extragalactic BH + WR candidates
|
||||||
| CXOU J123030.3+413853 | 6.4 | ? | 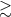 14.5 14.5 |
? | WR | [179] |
| (in NGC 4490) | ||||||
| CXOU J004732.0–251722.1 | 14 – 15 | ? | ? | ? | WR | [452] |
| (in NGC 253) | ||||||
2.4 A model-independent upper limit on the BH-BH/BH-NS coalescence rate
Even without using the population synthesis tool, one can search for NS + BH or BH + BH
progenitors among known BH in HMXB. This program has been pursued in [75, 32*], [33]. In these
papers, the authors examined the future evolution of two bright HMXB IC10 X-1/NGC300 X-1
found in nearby low-metallicity galaxies. Both binaries consist of massive WR-stars (about
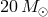 ) and BH in close orbits (orbital periods about 30 hours). Masses of WR-stars seem to
be high enough to produce the second BH, so these system may be immediate progenitors of
coalescing BH-BH systems. Analysis of the evolution of the best-known Galactic HMXB Cyg X-1
[32], which can be a NS + BH progenitor, led to the conclusion that the galactic formation
rate of coalescing NS + BH is likely to be very low, less than 1 per 100 Myrs. This estimate
is rather pessimistic, even for advanced LIGO detectors. Implications of the growing class of
short-period BH + WR binaries (see Table 4) for the (BH + BH)/(BH + NS) merger rate are discussed
in [452].
) and BH in close orbits (orbital periods about 30 hours). Masses of WR-stars seem to
be high enough to produce the second BH, so these system may be immediate progenitors of
coalescing BH-BH systems. Analysis of the evolution of the best-known Galactic HMXB Cyg X-1
[32], which can be a NS + BH progenitor, led to the conclusion that the galactic formation
rate of coalescing NS + BH is likely to be very low, less than 1 per 100 Myrs. This estimate
is rather pessimistic, even for advanced LIGO detectors. Implications of the growing class of
short-period BH + WR binaries (see Table 4) for the (BH + BH)/(BH + NS) merger rate are discussed
in [452].
While for NS-binary systems it is possible to obtain the upper limit for the coalescence rate based on
observed pulsar binary statistics (the Bailes limit, see Section 2.2 above), it is not so easy for BH + NS or
BH + BH systems due to the (present-day) lack of their observational candidates. Still, a crude estimate can
be found from the following considerations. A rough upper limit on the coalescence rate of BH + NS(BH)
binaries is set by the observed formation rate of high-mass X-ray binaries, their direct progenitors. The
present-day formation rate of galactic HMXBs is about 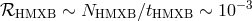 per year (here
we conservatively assumed
per year (here
we conservatively assumed 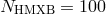 and
and 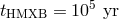 ). This estimate can be made more
precise considering that only very close compact binary systems can coalesce in the Hubble
time, which requires a common envelope stage after the HMXB stage to occur (see Figure 7*).
The CE stage is likely to happen in sufficiently close binaries after the bright X-ray accretion
stage.12
The analysis of observations of different X-ray–source populations in the galaxies suggests ([243] and
references therein) that only a few per cent of all BHs formed in a galaxy can pass through a bright
accretion stage in HMXBs. For a galactic NS formation rate of once per several decades, a minimum BH
progenitor mass of
). This estimate can be made more
precise considering that only very close compact binary systems can coalesce in the Hubble
time, which requires a common envelope stage after the HMXB stage to occur (see Figure 7*).
The CE stage is likely to happen in sufficiently close binaries after the bright X-ray accretion
stage.12
The analysis of observations of different X-ray–source populations in the galaxies suggests ([243] and
references therein) that only a few per cent of all BHs formed in a galaxy can pass through a bright
accretion stage in HMXBs. For a galactic NS formation rate of once per several decades, a minimum BH
progenitor mass of  and the Salpeter initial mass function, this yields an estimate of a few
and the Salpeter initial mass function, this yields an estimate of a few  per year. The probability of a given progenitor HMXB becoming a merging NS + BH or BH + BH
binary is very model-dependent. For example, recent studies of a unique galactic microquasar
SS 433 [58, 101] suggest the BH mass in such a system to be at least
per year. The probability of a given progenitor HMXB becoming a merging NS + BH or BH + BH
binary is very model-dependent. For example, recent studies of a unique galactic microquasar
SS 433 [58, 101] suggest the BH mass in such a system to be at least 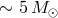 and the optical star
mass to be above
and the optical star
mass to be above  . In SS 433, the optical star fills the Roche lobe and forms a supercritical
accretion disk [183]. The mass transfer rate onto the compact star is estimated to be about
. In SS 433, the optical star fills the Roche lobe and forms a supercritical
accretion disk [183]. The mass transfer rate onto the compact star is estimated to be about
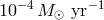 . According to the canonical HMXB evolution calculations, a common envelope must have
been formed in such a binary on a short time scale (thousands of years) (see Section 3.5 and [319]), but the
observed stability of binary-system parameters in SS433 over 30 years [132] shows that this is not the case.
This example clearly illustrates the uncertainty in our understanding of HMXB evolution with
BHs.
. According to the canonical HMXB evolution calculations, a common envelope must have
been formed in such a binary on a short time scale (thousands of years) (see Section 3.5 and [319]), but the
observed stability of binary-system parameters in SS433 over 30 years [132] shows that this is not the case.
This example clearly illustrates the uncertainty in our understanding of HMXB evolution with
BHs.
Thus, we conclude that in the most optimistic case where the (NS + BH)/(BH + BH) merger rate is
equal to the formation rate of their HMXB progenitors, the upper limit for Galactic 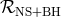 is a few
is a few
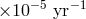 . The detection or non-detection of such binaries within
. The detection or non-detection of such binaries within  1000 Mpc distance by the
advanced LIGO detectors can therefore very strongly constrain our knowledge of the evolution of HMXB
systems.
1000 Mpc distance by the
advanced LIGO detectors can therefore very strongly constrain our knowledge of the evolution of HMXB
systems.

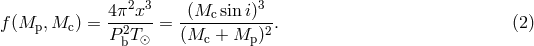

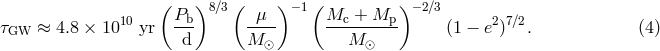
![−3 ℛV ≃ 0.01ℛG [Mpc ]. (5 )](article137x.gif)
![( )3 ( ) --Mx-sin3i-- -Pb-- 3 23∕2 −7 -Kv--- -Pb 2 3∕2 f(Mv ) = (Mx + Mv )2 = 2πG K v(1 − e ) ≈ 1.038 × 10 [M ⊙] km/s 1d (1 − e ) . (6 )](article157x.gif)