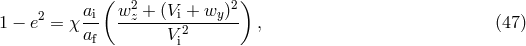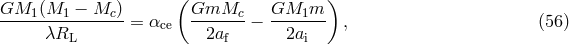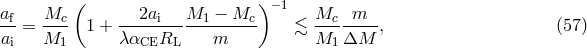3 Basic Principles of the Evolution of Binary Stars
Beautiful early general reviews of the topic can be found, e.g., in [45, 795*] and more later ones, e.g., in [755, 171, 799]. Here we restrict ourselves to recalling several facts concerning binary evolution that are most relevant to the formation and evolution of compact binaries. We will not discuss possible dynamical effects on binary evolution (like the Kozai–Lidov mechanism of eccentricity change in hierarchical triple systems, see e.g., [693]). Readers with experience in the field can skip this section.
3.1 Keplerian binary system and radiation back reaction
We start with some basic facts about Keplerian motion in a binary system and the simplest case of the
evolution of two point masses due to gravitational radiation losses. The stars are highly condensed objects,
so their treatment as point masses is usually adequate for the description of their interaction in the
binary. Furthermore, Newtonian gravitation theory is sufficient for this purpose as long as the
orbital velocities are small compared to the speed of light  . The systematic change of the
orbit caused by the emission of gravitational waves will be considered in a separate paragraph
below.
. The systematic change of the
orbit caused by the emission of gravitational waves will be considered in a separate paragraph
below.
3.1.1 Keplerian motion
Let us consider two point masses 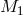 and
and 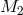 orbiting each other under the force of gravity. It is well
known (see [404]) that this problem is equivalent to the problem of a single body with mass
orbiting each other under the force of gravity. It is well
known (see [404]) that this problem is equivalent to the problem of a single body with mass 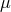 moving in
an external gravitational potential. The value of the external potential is determined by the total mass of
the system
moving in
an external gravitational potential. The value of the external potential is determined by the total mass of
the system
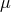 is
The body
is
The body 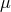 moves in an elliptic orbit with eccentricity
moves in an elliptic orbit with eccentricity  and major semi-axis
and major semi-axis  . The orbital
period
. The orbital
period 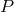 and orbital frequency
and orbital frequency 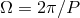 are related to
are related to 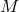 and
and  by Kepler’s third law
This relationship is valid for any eccentricity
by Kepler’s third law
This relationship is valid for any eccentricity  .
.
Individual bodies 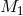 and
and 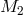 move around the barycenter of the system in elliptic orbits with the
same eccentricity
move around the barycenter of the system in elliptic orbits with the
same eccentricity  . The major semi-axes
. The major semi-axes 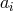 of the two ellipses are inversely proportional to the masses
of the two ellipses are inversely proportional to the masses
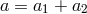 . The position vectors of the bodies from the system’s barycenter
are
. The position vectors of the bodies from the system’s barycenter
are 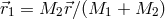 and
and 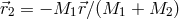 , where
, where 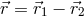 is the relative position
vector. Therefore, the velocities of the bodies with respect to the system’s barycentre are related by
and the relative velocity is
is the relative position
vector. Therefore, the velocities of the bodies with respect to the system’s barycentre are related by
and the relative velocity is 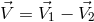 .
.
The total conserved energy of the binary system is
where is the distance between the bodies. The orbital angular momentum vector is perpendicular to the
orbital plane and can be written as
The absolute value of the orbital angular momentum is
is the distance between the bodies. The orbital angular momentum vector is perpendicular to the
orbital plane and can be written as
The absolute value of the orbital angular momentum is
For circular binaries with 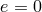 the distance between orbiting bodies does not depend on
time,
the distance between orbiting bodies does not depend on
time,
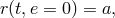
and is usually referred to as orbital separation. In this case, the velocities of the bodies, as well as their relative velocity, are also time-independent,
and the orbital angular momentum becomes
3.1.2 Gravitational radiation from a binary
The plane of the orbit is determined by the orbital angular momentum vector 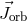 . The line of
sight is defined by a unit vector
. The line of
sight is defined by a unit vector 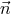 . The binary inclination angle
. The binary inclination angle 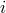 is defined by the relation
is defined by the relation
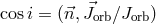 such that
such that 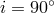 corresponds to a system visible edge-on.
corresponds to a system visible edge-on.
Let us start from two point masses  and
and  in a circular orbit. In the quadrupole
approximation [405*], the two polarization amplitudes of GWs at a distance
in a circular orbit. In the quadrupole
approximation [405*], the two polarization amplitudes of GWs at a distance  from the source are given
by
from the source are given
by
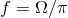 is the frequency of the emitted GWs (twice the orbital frequency). Note that for a fixed
distance
is the frequency of the emitted GWs (twice the orbital frequency). Note that for a fixed
distance  and a given frequency
and a given frequency 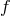 , the GW amplitudes are fully determined by
, the GW amplitudes are fully determined by 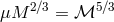 ,
where the combination
,
where the combination
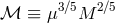
is called the “chirp mass” of the binary. After averaging over the orbital period (so that the squares of periodic functions are replaced by 1/2) and the orientations of the binary orbital plane, one arrives at the averaged (characteristic) GW amplitude
3.1.3 Energy and angular momentum loss
In the approximation and under the choice of coordinates that we are working with, it is sufficient to use
the Landau–Lifshitz gravitational pseudo-tensor [405*] when calculating the gravitational waves energy and
flux. (This calculation can be justified with the help of a fully satisfactory gravitational energy-momentum
tensor that can be derived in the field theory formulation of general relativity [17]). The energy 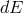 carried by a gravitational wave along its direction of propagation per area
carried by a gravitational wave along its direction of propagation per area 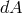 per time
per time 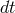 is given by
is given by
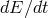 from a localized source in all directions is given by the integral
Replacing
from a localized source in all directions is given by the integral
Replacing
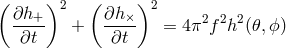
and introducing
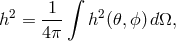
we write Eq. (22*) in the form
Specifically for a binary system in a circular orbit, one finds the energy loss from the system (sign minus) with the help of Eqs. (23*) and (20*):
This expression is exactly the same that can be obtained directly from the quadrupole formula [405], rewritten using the definition of the chirp mass and Kepler’s law. Since energy and angular momentum are continuously carried away by gravitational radiation, the two masses in orbit spiral towards each other, thus increasing their orbital frequency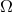 . The GW frequency
. The GW frequency 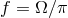 and the
GW amplitude
and the
GW amplitude 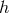 are also increasing functions of time. The rate of the frequency change
is13
are also increasing functions of time. The rate of the frequency change
is13
In spectral representation, the flux of energy per unit area per unit frequency interval is given by the right-hand-side of the expression
where we have introduced the spectral density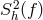 of the gravitational wave field
of the gravitational wave field 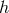 . In the case of a
binary system, the quantity
. In the case of a
binary system, the quantity 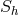 is calculable from Eqs. (18* and 19*):
is calculable from Eqs. (18* and 19*):
3.1.4 Binary coalescence time
A binary system in a circular orbit loses energy according to Eq. (24*). For orbits with non-zero eccentricity
 , the right-hand-side of this formula should be multiplied by the factor
, the right-hand-side of this formula should be multiplied by the factor
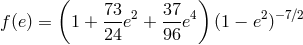
(see [579*]). The initial binary separation 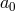 decreases and, assuming Eq. (25*) is always valid, the binary
should vanish in a time
decreases and, assuming Eq. (25*) is always valid, the binary
should vanish in a time
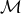 , which can also be
written as
, which can also be
written as 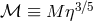 , where
, where 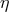 is the dimensionless ratio
is the dimensionless ratio 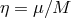 . Since
. Since 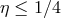 , one has
, one has
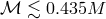 . For example, for two NSs with equal masses
. For example, for two NSs with equal masses 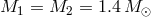 , the chirp mass is
, the chirp mass is
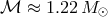 . This explains the choice of normalization in Eq. (29*).
. This explains the choice of normalization in Eq. (29*).
The coalescence time for a binary star with an initially eccentric orbit with 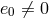 and initial
separation
and initial
separation 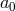 is shorter than the coalescence time for an object with a circular orbit and the same
is shorter than the coalescence time for an object with a circular orbit and the same
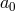 [579]:
[579]:
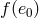 is
To merge in a time interval shorter than 10 Gyr the binary should have a small enough initial orbital
period
is
To merge in a time interval shorter than 10 Gyr the binary should have a small enough initial orbital
period 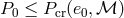 and, accordingly, a small enough initial semi-major axis
and, accordingly, a small enough initial semi-major axis 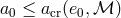 . The
critical orbital period is plotted as a function of the initial eccentricity
. The
critical orbital period is plotted as a function of the initial eccentricity 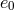 in Figure 3*. The lines are
plotted for three typical sets of masses: two neutron stars with equal masses (
in Figure 3*. The lines are
plotted for three typical sets of masses: two neutron stars with equal masses (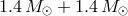 ), a black
hole and a neutron star (
), a black
hole and a neutron star (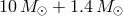 ), and two black holes with equal masses (
), and two black holes with equal masses (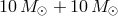 ).
Note that in order to get a significantly shorter coalescence time, the initial binary eccentricity should be
).
Note that in order to get a significantly shorter coalescence time, the initial binary eccentricity should be
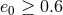 .
.
3.1.5 Magnetic stellar wind
In the case of low-mass binary evolution, there is another important physical mechanism responsible for the
removal of orbital angular momentum, in addition to the GW emission discussed above. This is the
magnetic stellar wind (MSW), or magnetic braking, which is thought to be effective for main-sequence G-M
dwarfs with convective envelopes, i.e., approximately, in the mass interval 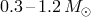 . The upper mass
limit corresponds to the disappearance of a deep convective zone, while the lower mass limit stands for
fully convective stars. In both cases a dynamo mechanism, responsible for enhanced magnetic
activity, is thought to become ineffective. The idea behind angular momentum loss (AML) by
magnetically-coupled stellar wind is that the stellar wind is compelled by magnetic field to corotate with the
star to rather large distances, where it carries away large specific angular momentum [680].
Thus, it appears possible to take away substantial angular momentum without evolutionarily
significant mass-loss in the wind. In the quantitative form, the concept of angular momentum
loss by MSW as a driver of the evolution of compact binaries was introduced by Verbunt and
Zwaan [810*] when it became evident that momentum loss by GWs is unable to explain the
observed mass-transfer rates in cataclysmic variables (CVs) and low-mass X-ray binaries, as well
as the deficit of cataclysmic variables with orbital periods between 2 and 3 hr (the “period
gap”).14
Verbunt and Zwaan based their reasoning on observations of the spin-down of rotation of single G-dwarfs in
stellar clusters with age, which is expressed by the phenomenological dependence of the equatorial
rotational velocity
. The upper mass
limit corresponds to the disappearance of a deep convective zone, while the lower mass limit stands for
fully convective stars. In both cases a dynamo mechanism, responsible for enhanced magnetic
activity, is thought to become ineffective. The idea behind angular momentum loss (AML) by
magnetically-coupled stellar wind is that the stellar wind is compelled by magnetic field to corotate with the
star to rather large distances, where it carries away large specific angular momentum [680].
Thus, it appears possible to take away substantial angular momentum without evolutionarily
significant mass-loss in the wind. In the quantitative form, the concept of angular momentum
loss by MSW as a driver of the evolution of compact binaries was introduced by Verbunt and
Zwaan [810*] when it became evident that momentum loss by GWs is unable to explain the
observed mass-transfer rates in cataclysmic variables (CVs) and low-mass X-ray binaries, as well
as the deficit of cataclysmic variables with orbital periods between 2 and 3 hr (the “period
gap”).14
Verbunt and Zwaan based their reasoning on observations of the spin-down of rotation of single G-dwarfs in
stellar clusters with age, which is expressed by the phenomenological dependence of the equatorial
rotational velocity 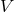 on age:
on age: 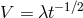 (“Skumanich law” [718]). In the latter formula
(“Skumanich law” [718]). In the latter formula 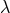 is an
empirically-derived coefficient
is an
empirically-derived coefficient 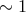 . Applying this to a binary component and assuming tidal locking
between the stellar axial rotation and orbital motion, one arrives at the rate of angular momentum loss via
MSW
. Applying this to a binary component and assuming tidal locking
between the stellar axial rotation and orbital motion, one arrives at the rate of angular momentum loss via
MSW
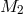 and
and 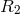 are the mass and radius of the optical component of the system, respectively,
are the mass and radius of the optical component of the system, respectively,
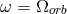 is the spin frequency of the star’s rotation equal to the binary orbital frequency, and
is the spin frequency of the star’s rotation equal to the binary orbital frequency, and 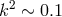 is the gyration radius of the optical component squared.
is the gyration radius of the optical component squared.
Radii of stars filling their Roche lobes should be proportional to binary separations, 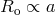 , which
means that the time scale of orbital angular momentum removal by MSW is
, which
means that the time scale of orbital angular momentum removal by MSW is 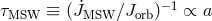 .
This should be compared with AML by GWs with
.
This should be compared with AML by GWs with 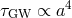 . Clearly, MSW (if it operates) is more
efficient at removing angular momentum from a binary system at larger separations (orbital periods), and
at small orbital periods GWs always dominate. Magnetic braking is especially important in CVs and in
LMXBs with orbital periods exceeding several hours and is the driving mechanism for mass accretion onto
the compact component. Indeed, the Doppler tomography reconstruction of the Roche-lobe–filling low-mass
K7 secondary star in a well-studied LMXB Cen X-4 revealed the presence of cool spots on
its surface. The latter provide evidence for the action of magnetic fields at the surface of the
star, thus supporting magnetic braking as the driving mechanism of mass exchange in this
binary [689].
. Clearly, MSW (if it operates) is more
efficient at removing angular momentum from a binary system at larger separations (orbital periods), and
at small orbital periods GWs always dominate. Magnetic braking is especially important in CVs and in
LMXBs with orbital periods exceeding several hours and is the driving mechanism for mass accretion onto
the compact component. Indeed, the Doppler tomography reconstruction of the Roche-lobe–filling low-mass
K7 secondary star in a well-studied LMXB Cen X-4 revealed the presence of cool spots on
its surface. The latter provide evidence for the action of magnetic fields at the surface of the
star, thus supporting magnetic braking as the driving mechanism of mass exchange in this
binary [689].
Equation (32*) with assumed 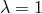 and
and 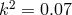 [627*] is often considered as a “standard”.
However, Eqs. (25*) and (32*) do not allow one to reproduce some observed features of CVs, see, e.g.,
[627, 600, 434, 771, 368], but the reasons for this discrepant behavior are not clear as yet. Recently,
Knigge et al. [368], based on the study of properties of donors in CVs, suggested that a better description
of the evolution of CVs is provided by scaling Eq. (32*) by a factor of
[627*] is often considered as a “standard”.
However, Eqs. (25*) and (32*) do not allow one to reproduce some observed features of CVs, see, e.g.,
[627, 600, 434, 771, 368], but the reasons for this discrepant behavior are not clear as yet. Recently,
Knigge et al. [368], based on the study of properties of donors in CVs, suggested that a better description
of the evolution of CVs is provided by scaling Eq. (32*) by a factor of 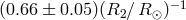 above the
period gap and by scaling Eq. (25*) by a factor
above the
period gap and by scaling Eq. (25*) by a factor 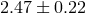 below the gap (where AML by MSW is not
acting). Note that these “semi-empirical”, as called by the their authors, numerical factors must be taken
with some caution, since they are based on the fitting of the
below the gap (where AML by MSW is not
acting). Note that these “semi-empirical”, as called by the their authors, numerical factors must be taken
with some caution, since they are based on the fitting of the 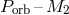 relation for observed stars
by a single evolutionary sequence with the initially-unevolved donor with
relation for observed stars
by a single evolutionary sequence with the initially-unevolved donor with 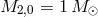 and
and
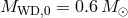 .
.
The simplest reason for deviation of AML by MSW from Eq. (25*) may be the unjustified extrapolation of stellar-rotation rates over several orders of magnitude – from slowly-rotating single field stars to rapidly-spinning components of close binaries. For the shortest orbital periods of binaries meant to evolve due to AML via GW, the presence of circumbinary discs may enhance their orbital angular momentum loss [841].
3.2 Mass exchange in close binaries
As mentioned in the introductory Section 1, all binaries may be considered either as “close” or as “wide”. In the former case, mass exchange between the components can occur. This process can be accompanied by mass and angular momentum loss from the system.
The shape of the stellar surface is determined by the shape of the equipotential level surface
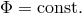 Conventionally, the total potential, which includes gravitational and centrifugal forces is
approximated by the Roche potential (see, e.g., [375*]), which is defined under the following
assumptions:
Conventionally, the total potential, which includes gravitational and centrifugal forces is
approximated by the Roche potential (see, e.g., [375*]), which is defined under the following
assumptions:
the gravitational field of two components is approximated by that of two point masses;
the binary orbit is circular;
the components of the system corotate with the binary orbital period.
Let us consider a Cartesian reference frame (x,y,z) rotating with the binary, with the origin at the
primary 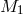 ; the x-axis is directed along the line of centers; the y-axis is aligned with the orbital motion
of the primary component; the z-axis is perpendicular to the orbital plane. The total potential at a given
point (x,y,z) is then
; the x-axis is directed along the line of centers; the y-axis is aligned with the orbital motion
of the primary component; the z-axis is perpendicular to the orbital plane. The total potential at a given
point (x,y,z) is then
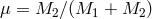 ,
, 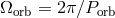 .
.
A 3-D representation of a dimensionless Roche potential in a co-rotating frame for a binary with mass
ratio of components 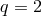 is shown in Figure 4*.
is shown in Figure 4*.
For close binary evolution the most important is the innermost level surface
that encloses both components. It defines the “critical”, or “Roche” lobes of the
components.15
Inside these lobes the matter is bound to the respective component. In the libration point 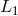 (the inner
Lagrangian point) the net force exerted onto a test particle corotating with the binary vanishes, so the
particle can escape from the surface of the star and be captured by the companion. The matter flows along
the surface of the Roche-lobe filling companion in the direction of
(the inner
Lagrangian point) the net force exerted onto a test particle corotating with the binary vanishes, so the
particle can escape from the surface of the star and be captured by the companion. The matter flows along
the surface of the Roche-lobe filling companion in the direction of 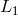 and escapes from the surface of the
contact component as a highly inhomogeneous stellar wind. Next, the wind forms a (supersonic) stream
directed at a certain angle respective to the line connecting the centers of the components. Depending on
the size of the second companion, the stream may hit the latter (called “direct impact”) or form a disk
orbiting the companion [448*].
and escapes from the surface of the
contact component as a highly inhomogeneous stellar wind. Next, the wind forms a (supersonic) stream
directed at a certain angle respective to the line connecting the centers of the components. Depending on
the size of the second companion, the stream may hit the latter (called “direct impact”) or form a disk
orbiting the companion [448*].
Though it is evident that mass exchange is a complex 3D gas-dynamical process that must also take into
account radiation transfer and, in some cases, even nuclear reactions, virtually all computations of the
evolution of non-compact close binaries have been performed in 1-D approximations. The Roche-lobe
overflow (RLOF) is conventionally considered to begin when the radius of an initially more
massive and hence faster evolving star (primary component) becomes equal to the radius of a
sphere with volume equal to that of the Roche lobe. For the latter, an expression precise to
better than 1% for an arbitrary mass ratio of components 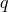 was suggested by Eggleton [172]:
was suggested by Eggleton [172]:
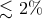 for
for 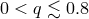 .
.
In close binaries, the zero-age main sequence (ZAMS) mass ceases to be the sole parameter determining
stellar evolution. The nature of compact remnants of close binary components also depends on their
evolutionary stage at RLOF, i.e., on the component separation and their mass-ratio 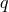 . Evolution of a star
may be considered as consumption of nuclear fuel accompanied by an increase of its radius.
Following the pioneering work of Kippenhahn and his collaborators on the evolution of close
binaries in the late 1960s, the following basic cases of mass exchange are usually considered: A –
RLOF at the core hydrogen-burning stage; B – RLOF at the hydrogen-shell burning stage; C –
RLOF after exhaustion of He in the stellar core. Also, more “fine” gradations exist: case AB –
RLOF at the late stages of core H-burning, which continues as Case B after a short break upon
exhaustion of H in the core; case BB – RLOF by the star, which first filled its Roche lobe in case
B, contracted under the Roche lobe after the loss of the hydrogen envelope, and resumed the
mass loss due to the envelope expansion at the helium-shell burning stage. Further, one may
consider the modes of mass-exchange, depending, e.g., on the nature of the envelope of the donor
(radiative vs. convective), its relative mass, reaction of accretor etc., see, e.g., [171, 826] and
Section 3.3.
. Evolution of a star
may be considered as consumption of nuclear fuel accompanied by an increase of its radius.
Following the pioneering work of Kippenhahn and his collaborators on the evolution of close
binaries in the late 1960s, the following basic cases of mass exchange are usually considered: A –
RLOF at the core hydrogen-burning stage; B – RLOF at the hydrogen-shell burning stage; C –
RLOF after exhaustion of He in the stellar core. Also, more “fine” gradations exist: case AB –
RLOF at the late stages of core H-burning, which continues as Case B after a short break upon
exhaustion of H in the core; case BB – RLOF by the star, which first filled its Roche lobe in case
B, contracted under the Roche lobe after the loss of the hydrogen envelope, and resumed the
mass loss due to the envelope expansion at the helium-shell burning stage. Further, one may
consider the modes of mass-exchange, depending, e.g., on the nature of the envelope of the donor
(radiative vs. convective), its relative mass, reaction of accretor etc., see, e.g., [171, 826] and
Section 3.3.
In cases A and B of mass exchange the remnants of stars with initial masses lower
than 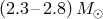 are degenerate He WD – a type of objects not produced by single
stars.16
are degenerate He WD – a type of objects not produced by single
stars.16
In cases A and B of mass exchange the remnants of stars with initial mass 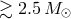 are helium
stars.
are helium
stars.
If the mass of the helium remnant star does not exceed 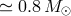 , after exhaustion of the He in the
core it does not expand, but transforms directly into a WD of the same mass [300*]. Helium stars with
masses between
, after exhaustion of the He in the
core it does not expand, but transforms directly into a WD of the same mass [300*]. Helium stars with
masses between 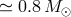 and
and 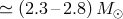 expand in the helium shell burning stage,
re-fill their Roche lobes, lose the remnants of the helium envelopes and also transform into CO
WD.
expand in the helium shell burning stage,
re-fill their Roche lobes, lose the remnants of the helium envelopes and also transform into CO
WD.
Stellar radius may be taken as a proxy for the evolutionary state of a star. We plot in Figure 5* the types of stellar remnant as a function of both initial mass and the radius of a star at the instant of RLOF. In Figure 6* initial-final mass relations for components of close binaries are shown. Clearly, relations presented in these two figures are only approximate, reflecting current uncertainty in the theory of stellar evolution (in this particular case, relations used in the population synthesis code IBiS [791*] are shown.
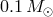 , the boundary between CO and ONe varieties
of WDs and WD and NSs – by
, the boundary between CO and ONe varieties
of WDs and WD and NSs – by 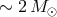 . The boundary between progenitors of NS and BH is shown
at
. The boundary between progenitors of NS and BH is shown
at 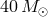 after [643], while it may be possible that it really is between
after [643], while it may be possible that it really is between 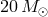 and
and 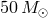 (see
Section 1 for discussion and references.)
(see
Section 1 for discussion and references.)3.3 Mass transfer modes and mass and angular momentum loss in binary systems
GW emission is the sole factor responsible for the change of orbital parameters of a detached pair of compact (degenerate) stars. However, it was recognized quite early on that in the stages of evolution preceding the formation of compact objects, the mode of mass transfer between the components and the loss of matter and orbital angular momentum by the system as a whole play a dominant dynamical role and define the observed features of the binaries, e.g., [556, 781, 631*, 471, 603, 137].
Strictly speaking, as mentioned previously, these processes should be treated hydrodynamically and they
require complicated numerical calculations. However, binary evolution can also be described
semi-qualitatively, using a simplified description in terms of point-like bodies. The change of their
integrated physical quantities, such as masses, orbital angular momentum, etc., governs the
evolution of the orbit. This description turns out to be successful in reproducing the results
of more rigorous numerical calculations (see, e.g., [705] for more details and references). In
this approach, the key role is allocated to the total orbital angular momentum 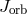 of the
binary.
of the
binary.
Let star 2 lose matter at a rate 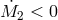 and let
and let 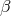
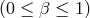 be the fraction of the ejected
matter that leaves the system (the rest falls on the first star), i.e.,
be the fraction of the ejected
matter that leaves the system (the rest falls on the first star), i.e.,  . Consider
circular orbits with orbital angular momentum given by Eq. (17*). Differentiate both parts of Eq. (17*) by
time
. Consider
circular orbits with orbital angular momentum given by Eq. (17*). Differentiate both parts of Eq. (17*) by
time 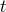 and exclude
and exclude 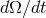 with the help of Kepler’s third law (10*). This gives the rate of change of the
orbital separation:
with the help of Kepler’s third law (10*). This gives the rate of change of the
orbital separation:
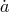 and
and 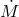 are not independent variables if the donor fills its Roche lobe. One defines the
mass transfer as conservative if both
are not independent variables if the donor fills its Roche lobe. One defines the
mass transfer as conservative if both 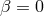 and
and 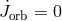 . The mass transfer is called non-conservative if
at least one of these conditions is violated.
. The mass transfer is called non-conservative if
at least one of these conditions is violated.
It is important to distinguish some specific cases (modes) of mass transfer:
- conservative mass transfer,
- non-conservative Jeans mode of mass loss (or fast wind mode),
- non-conservative isotropic re-emission,
- sudden mass loss from one of the components during supernova explosion, and
- common-envelope stage.
As specific cases of angular momentum loss we consider GW emission (see Section 3.1.3 and 3.1.4) and the magnetically-coupled stellar wind (see Section 3.1.5), which drive the orbital evolution for short-period binaries. For non-conservative modes, one can also consider some less important cases, such as, for instance, the formation of a circumbinary ring by the matter leaving the system (see, e.g., [722*, 732]). Here, we will not go into details of such sub-cases.
3.3.1 Conservative accretion
In the case of conservative accretion, matter from 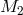 is fully deposited onto
is fully deposited onto 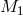 . The transfer process
preserves the total mass (
. The transfer process
preserves the total mass (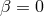 ) and the orbital angular momentum of the system. It follows from
Eq. (36*) that
) and the orbital angular momentum of the system. It follows from
Eq. (36*) that
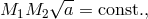
so that the initial and final binary separations are related as
The orbit shrinks when the more massive component loses matter, and the orbit widens in the opposite situation. During such a mass exchange, the orbital separation passes through a minimum, if the masses become equal in the course of mass transfer.
3.3.2 The Jeans (fast wind) mode
In this mode the matter ejected by the donor completely escapes from the system, that is, 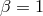 . Escape
of the matter can occur either via fast isotropic spherically-symmetric wind or in the form of bipolar jets
moving from the system at high velocity. Escaping matter does not interact with another component. The
matter escapes with the specific angular momentum of the mass-losing star
. Escape
of the matter can occur either via fast isotropic spherically-symmetric wind or in the form of bipolar jets
moving from the system at high velocity. Escaping matter does not interact with another component. The
matter escapes with the specific angular momentum of the mass-losing star 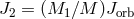 (we neglect
a possible proper rotation of the star, see [795]). For the loss of orbital momentum
(we neglect
a possible proper rotation of the star, see [795]). For the loss of orbital momentum 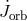 it is reasonable to
take
it is reasonable to
take
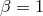 , Eq. (36*) can be written as
Then Eq. (39*) in conjunction with Eq. (38*) gives
, Eq. (36*) can be written as
Then Eq. (39*) in conjunction with Eq. (38*) gives 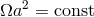 , that is,
, that is, 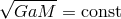 . Thus, as a
result of the Jeans mode of mass loss, the change in orbital separation is
Since the total mass decreases, the orbit always widens.
. Thus, as a
result of the Jeans mode of mass loss, the change in orbital separation is
Since the total mass decreases, the orbit always widens.
3.3.3 Isotropic re-emission
The matter lost by star 2 can first accrete onto star 1, and then, a fraction 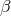 of the accreted matter, can
be expelled from the system. This happens, for instance, when a massive star transfers matter onto a
compact star on the thermal timescale (usually
of the accreted matter, can
be expelled from the system. This happens, for instance, when a massive star transfers matter onto a
compact star on the thermal timescale (usually  106 years). Accretion luminosity may exceed the
Eddington luminosity limit, and the radiation pressure pushes the infalling matter away from the system, in
a manner similar to the spectacular example of the SS 433 binary system. Other examples may be
systems with helium stars transferring mass onto relativistic objects [442*, 238]. In this mode of
mass-transfer, the binary orbital momentum carried away by the expelled matter is determined by the
orbital momentum of the accreting star rather than by the orbital momentum of the mass-losing star, since
mass loss happens in the vicinity of the accretor. The assumption that all matter in excess of accretion
rate can be expelled from the system, thus avoiding the formation of a common envelope, will
only hold if the liberated accretion energy of the matter falling from the Roche lobe radius of
the accretor star to its surface is sufficient to expel the matter from the Roche-lobe surface
around the accretor, i.e.,
106 years). Accretion luminosity may exceed the
Eddington luminosity limit, and the radiation pressure pushes the infalling matter away from the system, in
a manner similar to the spectacular example of the SS 433 binary system. Other examples may be
systems with helium stars transferring mass onto relativistic objects [442*, 238]. In this mode of
mass-transfer, the binary orbital momentum carried away by the expelled matter is determined by the
orbital momentum of the accreting star rather than by the orbital momentum of the mass-losing star, since
mass loss happens in the vicinity of the accretor. The assumption that all matter in excess of accretion
rate can be expelled from the system, thus avoiding the formation of a common envelope, will
only hold if the liberated accretion energy of the matter falling from the Roche lobe radius of
the accretor star to its surface is sufficient to expel the matter from the Roche-lobe surface
around the accretor, i.e., 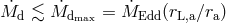 , where
, where 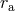 is the radius of the accretor
[364].
is the radius of the accretor
[364].
The orbital momentum loss can be written as
where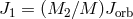 is the orbital momentum of the star
is the orbital momentum of the star 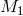 . In the limiting case when all the mass
initially accreted by
. In the limiting case when all the mass
initially accreted by 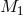 is later expelled from the system,
is later expelled from the system, 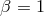 , Eq. (41*) simplifies to
After substitution of this formula into Eq. (36*) and integration over time, one arrives at
The exponential term makes this mode of mass transfer very sensitive to the components’ mass ratio. If
, Eq. (41*) simplifies to
After substitution of this formula into Eq. (36*) and integration over time, one arrives at
The exponential term makes this mode of mass transfer very sensitive to the components’ mass ratio. If
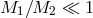 , the separation
, the separation  between the stars may decrease so much that the approximation of point
masses becomes invalid. Tidal orbital instability (Darwin instability) may set in, and the compact
star’s may start spiraling toward the companion star centre (the common envelope stage; see
Section 3.6). On the other hand, “isotropic reemission” may stabilize mass-exchange if
between the stars may decrease so much that the approximation of point
masses becomes invalid. Tidal orbital instability (Darwin instability) may set in, and the compact
star’s may start spiraling toward the companion star centre (the common envelope stage; see
Section 3.6). On the other hand, “isotropic reemission” may stabilize mass-exchange if 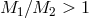 [877*].
[877*].
Mass loss may be considered as occurring in the “isotropic re-emission” mode in situations in which hot white dwarf components of cataclysmic variables lose mass by optically-thick winds [346*] or when time-averaged mass loss from novae is considered [867].
3.4 Supernova explosion
Supernovae explosions in binary systems occur on a timescale much shorter than the orbital period, so the loss of mass is practically instantaneous. This case can be treated analytically (see, e.g., [55, 59, 753]).
Clearly, even a spherically-symmetric sudden mass loss due to an SN explosion will be asymmetric in the
reference frame of the center of mass of the binary system, leading to system recoil (‘Blaauw–Boersma’
recoil). In general, the loss of matter and radiation is non-spherical, so that the remnant of the
supernova explosion (neutron star or black hole) acquires some recoil velocity called kick velocity
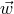 . In a binary, the kick velocity should be added to the orbital velocity of the pre-supernova
star.
. In a binary, the kick velocity should be added to the orbital velocity of the pre-supernova
star.
The usual treatment proceeds as follows. Let us consider a pre-SN binary with initial masses 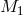 and
and 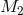 . The stars move in a circular orbit with orbital separation
. The stars move in a circular orbit with orbital separation 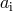 and relative velocity
and relative velocity
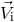 . The star
. The star 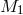 explodes leaving a compact remnant of mass
explodes leaving a compact remnant of mass 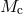 . The total mass of
the binary decreases by
. The total mass of
the binary decreases by 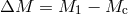 . Unless the binary is disrupted, it will end up in
a new orbit with eccentricity
. Unless the binary is disrupted, it will end up in
a new orbit with eccentricity  , semi-major axis
, semi-major axis 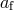 , and angle
, and angle 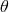 between the orbital
planes before and after the explosion. In general, the new barycenter will also receive some
velocity, but we neglect this motion. The goal is to evaluate the parameters
between the orbital
planes before and after the explosion. In general, the new barycenter will also receive some
velocity, but we neglect this motion. The goal is to evaluate the parameters 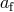 ,
,  , and
, and
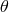 .
.
It is convenient to use an instantaneous reference frame centered on 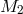 right at the time of explosion.
The
right at the time of explosion.
The 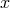 -axis is the line from
-axis is the line from 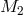 to
to 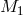 , the
, the 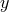 -axis points in the direction of
-axis points in the direction of 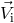 , and the
, and the  -axis is
perpendicular to the orbital plane. In this frame, the pre-SN relative velocity is
-axis is
perpendicular to the orbital plane. In this frame, the pre-SN relative velocity is 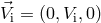 , where
, where
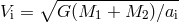 (see Eq. (16*)). The initial total orbital momentum is
(see Eq. (16*)). The initial total orbital momentum is 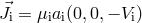 . The
explosion is considered to be instantaneous. Right after the explosion, the position vector of the
exploded star
. The
explosion is considered to be instantaneous. Right after the explosion, the position vector of the
exploded star 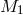 has not changed:
has not changed: 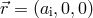 . However, other quantities have changed:
. However, other quantities have changed:
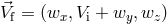 and
and 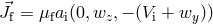 , where
, where 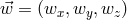 is the kick
velocity and
is the kick
velocity and 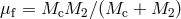 is the reduced mass of the system after explosion. The
parameters
is the reduced mass of the system after explosion. The
parameters 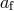 and
and  are found by equating the total energy and the absolute value of the orbital
momentum of the initial circular orbit to those of the resulting elliptical orbit (see Eqs. (13*, 17*, 15*)):
are found by equating the total energy and the absolute value of the orbital
momentum of the initial circular orbit to those of the resulting elliptical orbit (see Eqs. (13*, 17*, 15*)):
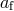 and
and  one finds
and
where
one finds
and
where 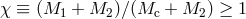 . The angle
. The angle 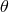 is defined by
is defined by

which results in
The condition for disruption of the binary system depends on the absolute value 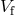 of the
final velocity, and on the parameter
of the
final velocity, and on the parameter 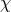 . The binary disrupts if its total energy defined by the
left-hand-side of Eq. (44*) becomes non-negative or, equivalently, if its eccentricity defined by Eq. (47*)
becomes
. The binary disrupts if its total energy defined by the
left-hand-side of Eq. (44*) becomes non-negative or, equivalently, if its eccentricity defined by Eq. (47*)
becomes 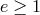 . From either of these requirements one derives the condition for disruption:
. From either of these requirements one derives the condition for disruption:
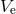 defined by the requirement
defined by the requirement
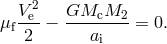
Since 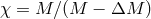 and
and 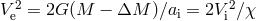 , one can write Eq. (49*) in the form
, one can write Eq. (49*) in the form
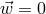 , and, therefore,
, and, therefore, 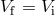 . In this case, Eq. (49*) reads
. In this case, Eq. (49*) reads 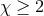 , which is
equivalent to
, which is
equivalent to 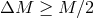 . Thus, the system unbinds if more than half of the mass of the binary is lost. In
other words, the resulting eccentricity
following from Eqs. (46*) and (47*), and
. Thus, the system unbinds if more than half of the mass of the binary is lost. In
other words, the resulting eccentricity
following from Eqs. (46*) and (47*), and  becomes larger than 1, if
becomes larger than 1, if 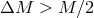 .
.
So far, we have considered an originally circular orbit. If the pre-SN star moves in an originally eccentric orbit, the condition of disruption of the system under symmetric explosion reads
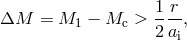
where  is the distance between the components at the moment of explosion.
is the distance between the components at the moment of explosion.
3.5 Kick velocity of neutron stars
The kick imparted to a NS at birth is one of the major problems in the theory of stellar evolution. By itself, it is an additional parameter, the introduction of which has been motivated first of all by high space velocities of radio pulsars inferred from the measurements of their proper motions and distances. Pulsars were recognized as a high-velocity Galactic population soon after their discovery in 1968 [256]. Shklovskii [704] put forward the idea that high pulsar velocities may result from asymmetric supernova explosions. Since then this hypothesis has been tested by pulsar observations, but no definite conclusions on its magnitude and direction have as yet been obtained.
Indeed, the distance to a pulsar is usually derived from the dispersion measure evaluation and crucially depends on the assumed model of electron density distribution in the Galaxy. In the middle of the 1990s, Lyne and Lorimer [449] derived a very high mean space velocity of pulsars with known proper motion of about 450 km s–1. This value was difficult to adopt without invoking an additional natal kick velocity of NSs.
The high mean space velocity of pulsars, consistent with earlier results by Lyne and Lorimer, was
confirmed by the analysis of a larger sample of pulsars [284]. The recovered distribution of 3D velocities is
well fit by a Maxwellian distribution with the mean value 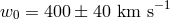 and a 1D rms
and a 1D rms
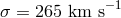 .
.
Possible physical reasons for natal NS kicks due to hydrodynamic effects in core-collapse supernovae are
summarized in [402, 401]. Large kick velocities (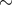 500 km s–1 and even more) imparted to nascent
NSs are generally confirmed by detailed numerical simulations (see, e.g., [536, 846]). Neutrino
effects in the strong magnetic field of a young NS may also be essential in explaining kicks
up to
500 km s–1 and even more) imparted to nascent
NSs are generally confirmed by detailed numerical simulations (see, e.g., [536, 846]). Neutrino
effects in the strong magnetic field of a young NS may also be essential in explaining kicks
up to 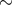 100 km s–1 [109, 160, 398]. Astrophysical arguments favoring a kick velocity are
also summarized in [754]. To get around the theoretical difficulty of insufficient rotation of
pre-supernova cores in single stars to produce rapidly-spinning young pulsars, Spruit and Phinney [731]
proposed that random off-center kicks can lead to a net spin-up of proto-NSs. In this model,
correlations between pulsar space velocity and rotation are possible and can be tested in further
observations.
100 km s–1 [109, 160, 398]. Astrophysical arguments favoring a kick velocity are
also summarized in [754]. To get around the theoretical difficulty of insufficient rotation of
pre-supernova cores in single stars to produce rapidly-spinning young pulsars, Spruit and Phinney [731]
proposed that random off-center kicks can lead to a net spin-up of proto-NSs. In this model,
correlations between pulsar space velocity and rotation are possible and can be tested in further
observations.
Here we should note that the existence of some kick follows not only from the measurements
of radio pulsar space velocities, but also from the analysis of binary systems with NSs. The
impact of a kick velocity 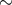 100 km s–1 explains the precessing pulsar binary orbit in
PSR J0045–7319 [345]. The evidence of the kick velocity is seen in the inclined, with
respect to the orbital plane, circumstellar disk around the Be star SS 2883 – an optical component
of a binary PSR B1259–63 [617]. Evidence for
100 km s–1 explains the precessing pulsar binary orbit in
PSR J0045–7319 [345]. The evidence of the kick velocity is seen in the inclined, with
respect to the orbital plane, circumstellar disk around the Be star SS 2883 – an optical component
of a binary PSR B1259–63 [617]. Evidence for 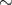 150 km s–1 natal kicks has also
been inferred from the statistics of the observed short GRB distributions relative to their host
galaxies [31].
150 km s–1 natal kicks has also
been inferred from the statistics of the observed short GRB distributions relative to their host
galaxies [31].
Long-term pulse profile changes interpreted as geodetic precession are observed in the relativistic pulsar binaries PSR 1913+16 [831], PSR B1534+12 [734], PSR J1141–6545 [289], and PSR J0737–3039B [78]. These observations indicate that in order to produce the misalignment between the orbital angular momentum and the neutron star spin, a component of the kick velocity perpendicular to the orbital plane is required [835, 839*, 840]. This idea seems to gain observational support from recent thorough polarization measurements [324] suggesting alignment of the rotational axes with the pulsar’s space velocity. Detailed discussion of the spin-velocity alignment in young pulsars and implications for the SN kick mechanisms can be found in Noutsos et al. [538]. Such an alignment acquired at birth may indicate the kick velocity directed preferably along the rotation of the proto-NS. For the first SN explosion in a close binary system this would imply that the kick is mostly perpendicular to the orbital plane. Implications of this effect for the formation and coalescence rates of NS binaries were discussed by Kuranov et al. [396].
It is worth noting that the analysis of the formation of the relativistic pulsar
binaryPSR J0737–3039 [595] may suggest, from the observed low eccentricity of the
system 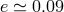 , that a small (if any) kick velocity may be acquired if the formation of the second NS in
the system is associated with the collapse of an ONeMg WD due to electron captures. The symmetric
nature of electron-capture supernovae was discussed in [597] and seems to be an interesting issue requiring
further studies (see, e.g., [582, 397] for the analysis of the formation of NSs in globular clusters in
the frame of this hypothesis). Note that electron-capture SNe are expected to be weak events,
irrespective of whether they are associated with the core collapse of a star that retained some original
envelope or with the AIC of a WD [644, 366, 146]. In the case of AIC, rapid rotation of a
collapsing object along with flux freezing and dynamo action can grow the WD’s magnetic
field to magnetar strengths during collapse. Further, magnetar generates outflow of the matter
and formation of a pulsar wind nebula, which may be observed as a radio-source for a few
month [592].
, that a small (if any) kick velocity may be acquired if the formation of the second NS in
the system is associated with the collapse of an ONeMg WD due to electron captures. The symmetric
nature of electron-capture supernovae was discussed in [597] and seems to be an interesting issue requiring
further studies (see, e.g., [582, 397] for the analysis of the formation of NSs in globular clusters in
the frame of this hypothesis). Note that electron-capture SNe are expected to be weak events,
irrespective of whether they are associated with the core collapse of a star that retained some original
envelope or with the AIC of a WD [644, 366, 146]. In the case of AIC, rapid rotation of a
collapsing object along with flux freezing and dynamo action can grow the WD’s magnetic
field to magnetar strengths during collapse. Further, magnetar generates outflow of the matter
and formation of a pulsar wind nebula, which may be observed as a radio-source for a few
month [592].
We also note the hypothesis of Pfahl et al. [583*], based on observations of high-mass X-ray binaries
with long orbital periods (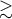 30 d) and low eccentricities (
30 d) and low eccentricities (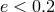 ), that rapidly rotating precollapse
cores may produce neutron stars with relatively small kicks, and vice versa for slowly rotating cores. Then,
large kicks would be a feature of stars that retained deep convective envelopes long enough
to allow a strong magnetic torque, generated by differential rotation between the core and
the envelope, to spin the core down to the very slow rotation rate of the envelope. A low kick
velocity imparted to the second (younger) neutron star (
), that rapidly rotating precollapse
cores may produce neutron stars with relatively small kicks, and vice versa for slowly rotating cores. Then,
large kicks would be a feature of stars that retained deep convective envelopes long enough
to allow a strong magnetic torque, generated by differential rotation between the core and
the envelope, to spin the core down to the very slow rotation rate of the envelope. A low kick
velocity imparted to the second (younger) neutron star (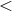 50 km s–1) was inferred from
the analysis of large-eccentricity pulsar binary PSR J1811–1736 [119]. The
large orbital period of this pulsar binary (18.8 d) may then suggest an evolutionary scenario
with inefficient (if any) common envelope stage [148], i.e., the absence of a deep convective
shell in the supernova progenitor (a He-star). This conclusion can be regarded as supportive
to ideas put forward by Pfahl et al. [583*]. A careful investigation of radio profiles of double
PSR J0737–3039A/B [198*] and Fermi detection of gamma-ray emission from the
recycled 22-ms pulsar [254] imply its spin axis to be almost aligned with the orbital angular momentum,
which lends further credence to the hypothesis that the second supernova explosion in this system was very
symmetric.
50 km s–1) was inferred from
the analysis of large-eccentricity pulsar binary PSR J1811–1736 [119]. The
large orbital period of this pulsar binary (18.8 d) may then suggest an evolutionary scenario
with inefficient (if any) common envelope stage [148], i.e., the absence of a deep convective
shell in the supernova progenitor (a He-star). This conclusion can be regarded as supportive
to ideas put forward by Pfahl et al. [583*]. A careful investigation of radio profiles of double
PSR J0737–3039A/B [198*] and Fermi detection of gamma-ray emission from the
recycled 22-ms pulsar [254] imply its spin axis to be almost aligned with the orbital angular momentum,
which lends further credence to the hypothesis that the second supernova explosion in this system was very
symmetric.
Small kicks in the case of  -capture in the O-Ne core leading to NS formation are justified
by hydrodynamical considerations. Indeed, already in 1996, Burrows and Hayes [80] noted
that large scale convective motions in O and Si burning stages preceding the formation of a Fe
core may produce inhomogeneities in the envelope of the protostellar core. They in turn may
result in asymmetric neutrino transport, which impart kicks up to 500 km s–1. Such a violent
burning does not precede the formation of O-Ne cores and then small or even zero kicks can be
expected.
-capture in the O-Ne core leading to NS formation are justified
by hydrodynamical considerations. Indeed, already in 1996, Burrows and Hayes [80] noted
that large scale convective motions in O and Si burning stages preceding the formation of a Fe
core may produce inhomogeneities in the envelope of the protostellar core. They in turn may
result in asymmetric neutrino transport, which impart kicks up to 500 km s–1. Such a violent
burning does not precede the formation of O-Ne cores and then small or even zero kicks can be
expected.
In the case of asymmetric core-collapse supernova explosion, it is natural to expect some kick during BH formation as well [430*, 214, 607*, 609*, 518*, 34*, 872*]. The similarity of NS and BH distribution in the Galaxy suggesting BH kicks was noted in [327]. Evidence for a moderate (100 – 200 km s–1) BH kick has been derived from the kinematics of several BH X-ray transients (microquasars): XTE J1118+180 [208], GRO 1655–40 [838], MAXI J1659–152 [400]. However, no kicks or only small ones seem to be required to explain the formation of other BH candidates, such as Cyg X-1 [485], [845], X-Nova Sco [514], V404 Cyg [484]. Population synthesis modeling of the Galactic distribution of BH binaries supports the need for (possibly, bimodal) natal BH kicks [634*]. Janka [321] argued that the similarity of BH kick distribution with NS kick distributions as inferred from the analysis by Repetto et al. [634*] favors BH kicks being due to gravitational interaction with asymmetric mass ejection (the “gravitational tug-boat mechanism”), and disfavors neutrino-induced kicks (in the last case, by momentum conservation, BH kicks are expected to be reduced by the NS to the BH mass ratio relative to the NS kicks). Facing current uncertainties in SN explosions and BH formation mechanisms, it is not excluded that low-kick BHs can be formed without associated SN explosions due to neutrino asymmetry, while high-velocity Galactic BHs in LMXBs analyzed by Repetto et al. [634] can be formed by the gravitational tug-boat mechanism suggested by Janka [321].
To summarize, the kick velocity remains to be one of the important unknown parameters of binary evolution with NSs and BHs, and further phenomenological input here is of great importance. Large kick velocities will significantly affect the spatial distribution of coalescing compact binaries (e.g., [352]) and BH kicks are extremely important for BH spin misalignment in coalescing BH-BH binary systems (e.g., Gerosa et al. [237] and references therein). Further constraining this parameter with various observations and a theoretical understanding of the possible asymmetry of core-collapse supernovae seem to be of paramount importance for the formation and evolution of close compact binaries.
3.5.1 Effect of the kick velocity on the evolution of a binary system
The collapse of a star to a BH, or its explosion leading to the formation of a NS, are normally considered as
instantaneous. This assumption is well justified in binary systems, since typical orbital velocities before the
explosion do not exceed a few hundred km/s, while most of the mass is expelled with velocities of about
several thousand km/s. The exploding star 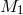 leaves the remnant
leaves the remnant 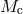 , and the binary
loses a part of its mass:
, and the binary
loses a part of its mass: 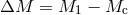 . The relative velocity of stars before the event is
. The relative velocity of stars before the event is
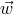 , the absolute value of
, the absolute value of 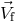 varies in the interval
from the smallest
varies in the interval
from the smallest 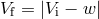 to the largest
to the largest 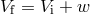 . The system gets disrupted if
. The system gets disrupted if 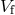 satisfies
the condition (see Section 3.4)
where
satisfies
the condition (see Section 3.4)
where 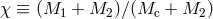 .
.
Let us start from the limiting case when the mass loss is practically zero (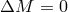 ,
, 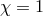 ), while a
non-zero kick velocity can still be present. This situation can be relevant to BH formation. It follows from
Eq. (54*) that, for relatively small kicks,
), while a
non-zero kick velocity can still be present. This situation can be relevant to BH formation. It follows from
Eq. (54*) that, for relatively small kicks, 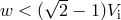 , the system always (independent of the direction
of
, the system always (independent of the direction
of 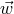 ) remains bound, while for
) remains bound, while for 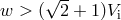 the system always decays. By averaging over equally
probable orientations of
the system always decays. By averaging over equally
probable orientations of 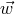 with a fixed amplitude
with a fixed amplitude 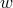 , one can show that in the particular case
, one can show that in the particular case 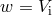 the system disrupts or survives with equal probabilities. If
the system disrupts or survives with equal probabilities. If 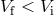 , the semi-major axis of the system
becomes smaller than the original binary separation,
, the semi-major axis of the system
becomes smaller than the original binary separation, 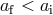 (see Eq. (46*)). This means that the system
becomes harder than before, i.e. it has a greater negative total energy than the original binary. If
(see Eq. (46*)). This means that the system
becomes harder than before, i.e. it has a greater negative total energy than the original binary. If
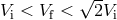 , the system remains bound, but
, the system remains bound, but 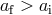 . For small and moderate kicks
. For small and moderate kicks
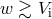 , the probabilities for the system to become more or less bound are approximately
equal.
, the probabilities for the system to become more or less bound are approximately
equal.
In general, the binary system loses some fraction of its mass 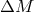 . In the absence of the kick, the
system remains bound if
. In the absence of the kick, the
system remains bound if 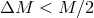 and gets disrupted if
and gets disrupted if 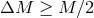 (see Section 3.4). Clearly, a
“properly” oriented kick velocity (directed against the vector
(see Section 3.4). Clearly, a
“properly” oriented kick velocity (directed against the vector 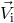 ) can keep the system bound, even if it
would have been disrupted without the kick. And, on the other hand, an “unfortunate” direction of
) can keep the system bound, even if it
would have been disrupted without the kick. And, on the other hand, an “unfortunate” direction of 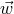 can
disrupt the system, which otherwise would stay bound.
can
disrupt the system, which otherwise would stay bound.
Consider, first, the case 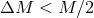 . The parameter
. The parameter 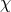 varies in the interval from 1 to 2, and the
escape velocity
varies in the interval from 1 to 2, and the
escape velocity 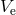 varies in the interval from
varies in the interval from 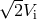 to
to 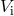 . It follows from Eq. (50*) that the
binary always remains bound if
. It follows from Eq. (50*) that the
binary always remains bound if 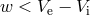 , and always unbinds if
, and always unbinds if 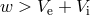 . This is a
generalization of the formulas derived above for the limiting case
. This is a
generalization of the formulas derived above for the limiting case 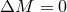 . Obviously, for a
given
. Obviously, for a
given 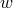 , the probability for the system to disrupt or become softer increases when
, the probability for the system to disrupt or become softer increases when 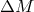 becomes larger. Now turn to the case
becomes larger. Now turn to the case 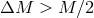 . The escape velocity of the compact star
becomes
. The escape velocity of the compact star
becomes 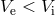 . The binary is always disrupted if the kick velocity is too large or too small:
. The binary is always disrupted if the kick velocity is too large or too small:
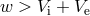 or
or 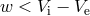 . However, for all intermediate values of
. However, for all intermediate values of 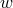 , the system can remain
bound, and sometimes even more hard than before, if the direction of
, the system can remain
bound, and sometimes even more hard than before, if the direction of 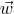 happened to be
approximately opposite to
happened to be
approximately opposite to 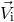 . A detailed calculation of the probabilities for the binary survival or
disruption requires integration over the kick velocity distribution function
. A detailed calculation of the probabilities for the binary survival or
disruption requires integration over the kick velocity distribution function 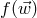 (see, e.g.,
[68]).
(see, e.g.,
[68]).
3.6 Common envelope stage
3.6.1 Formation of the common envelope
Common envelopes (CE) are definitely the most important (and not as yet solved) problem in the evolution
of close binaries. In the theory of stellar evolution, it was recognized quite early that there are several
situations when formation of an envelope that engulfs an entire system seems to be inevitable. It can
happen when the mass transfer rate from the mass-losing star is so high that the companion cannot
accommodate all the accreting matter [41, 868, 631*, 523, 823, 614, 590]. Another instance is encountered
when it is impossible to keep synchronous rotation of a red giant and orbital revolution of a compact
companion [730*, 8]. Because of tidal drag forces, the revolution period decreases, while the rotation period
increases in order to reach synchronism (Darwin instability). If the total orbital momentum of the binary
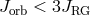 , the synchronism cannot be reached and the companion (low-mass star, white dwarf or
neutron star) spirals into the envelope of the red giant. Yet another situation is the formation of an
extended envelope, which enshrouds the system due to unstable nuclear burning at the surface
of an accreting WD in a compact binary [738, 559, 534]. It is also possible that a compact
remnant of a supernova explosion with “appropriately” directed kick velocity finds itself in an
elliptic orbit whose minimum periastron distance
, the synchronism cannot be reached and the companion (low-mass star, white dwarf or
neutron star) spirals into the envelope of the red giant. Yet another situation is the formation of an
extended envelope, which enshrouds the system due to unstable nuclear burning at the surface
of an accreting WD in a compact binary [738, 559, 534]. It is also possible that a compact
remnant of a supernova explosion with “appropriately” directed kick velocity finds itself in an
elliptic orbit whose minimum periastron distance 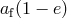 is smaller than the radius of the
companion.
is smaller than the radius of the
companion.
The common-envelope stage appears to be unavoidable on observational grounds. The evidence for a
dramatic orbital angular momentum decrease in the course of evolution follows immediately from
observations of cataclysmic variables, in which a white dwarf accretes matter from a small
red dwarf main-sequence companion, close binary nuclei of planetary nebulae, low-mass X-ray
binaries, and X-ray transients (neutron stars and black holes accreting matter from low-mass
main-sequence dwarfs). At present, the typical separation of components in these systems is
 , while the formation of compact stars requires progenitors with radii
, while the formation of compact stars requires progenitors with radii 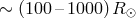 .
17
Indirect evidence for the common envelope stage comes, for instance, from X-ray and FUV observations of a
prototypical pre-cataclysmic binary V471 Tau showing anomalous C/N contamination of the
K-dwarf companion to white dwarf [164, 714].
.
17
Indirect evidence for the common envelope stage comes, for instance, from X-ray and FUV observations of a
prototypical pre-cataclysmic binary V471 Tau showing anomalous C/N contamination of the
K-dwarf companion to white dwarf [164, 714].
Let us consider the following mass-radius exponents that describe the response of a star to the mass loss in a binary system:
where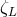 is the response of the Roche lobe to the mass loss,
is the response of the Roche lobe to the mass loss, 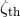 – the thermal-equilibrium response, and
– the thermal-equilibrium response, and
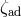 – the adiabatic hydrostatic response. If
– the adiabatic hydrostatic response. If 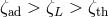 , the star retains hydrostatic equilibrium, but
does not remain in thermal equilibrium and mass loss occurs in the thermal timescale of the star. If
, the star retains hydrostatic equilibrium, but
does not remain in thermal equilibrium and mass loss occurs in the thermal timescale of the star. If
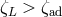 , the star cannot retain hydrostatic equilibrium and mass loss proceeds in the dynamical time
scale [558]. If both
, the star cannot retain hydrostatic equilibrium and mass loss proceeds in the dynamical time
scale [558]. If both 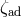 and
and 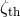 exceed
exceed 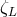 , mass loss occurs due to expansion of the star caused by
nuclear burning or due to the shrinkage of the Roche lobe owed to the angular momentum
loss.
, mass loss occurs due to expansion of the star caused by
nuclear burning or due to the shrinkage of the Roche lobe owed to the angular momentum
loss.
A high rate of mass overflow onto a compact star from a normal star is always expected when the
normal star goes off the main sequence and develops a deep convective envelope. The physical reason for
this is that convection tends to make entropy constant along the radius, so the radial structure of convective
stellar envelopes is well described by a polytrope (i.e., the equation of state can be written as
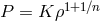 ) with an index
) with an index 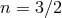 . The polytropic approximation with
. The polytropic approximation with 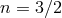 is also valid for
degenerate white dwarfs with masses not too close to the Chandrasekhar limit. For a star in
hydrostatic equilibrium, this results in the inverse mass-radius relation,
is also valid for
degenerate white dwarfs with masses not too close to the Chandrasekhar limit. For a star in
hydrostatic equilibrium, this results in the inverse mass-radius relation, 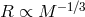 , first found for
white dwarfs. Removing mass from a star with a negative power of the mass-radius relation
increases its radius. On the other hand, the Roche lobe of the more massive star should shrink in
response to the conservative mass exchange between the components. This further increases the
mass loss rate from the Roche-lobe filling star leading to dynamical mass loss and eventual
formation of a common envelope. If the star is completely convective or completely degenerate,
dynamically-unstable mass loss occurs if the mass ratio of components (donor to accretor) is
, first found for
white dwarfs. Removing mass from a star with a negative power of the mass-radius relation
increases its radius. On the other hand, the Roche lobe of the more massive star should shrink in
response to the conservative mass exchange between the components. This further increases the
mass loss rate from the Roche-lobe filling star leading to dynamical mass loss and eventual
formation of a common envelope. If the star is completely convective or completely degenerate,
dynamically-unstable mass loss occurs if the mass ratio of components (donor to accretor) is
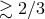 .
.
In a more realistic case when the star is not completely convective and has a radiative core, certain
insight may be gained by the analyses of composite polytropic models. Conditions for the onset of
dynamical mass loss become less rigorous [555, 283*, 722]: the contraction of a star replaces expansion if the
relative mass of the core 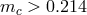 and in a binary with a mass ratio of components close to 1, a
Roche-lobe filling star with a deep convective envelope may remain dynamically stable if
and in a binary with a mass ratio of components close to 1, a
Roche-lobe filling star with a deep convective envelope may remain dynamically stable if 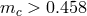 . As
well, a stabilizing effect upon mass loss may have mass and momentum loss from the system, if it
happens in a mode that results in an increase of the specific angular momentum of the binary
(e.g., in the case of isotropic reemission by a more massive component of the system in CVs or
UCXBs).
. As
well, a stabilizing effect upon mass loss may have mass and momentum loss from the system, if it
happens in a mode that results in an increase of the specific angular momentum of the binary
(e.g., in the case of isotropic reemission by a more massive component of the system in CVs or
UCXBs).
Criteria for thermal or dynamical mass loss upon RLOF and the formation of a common envelope need systematic exploration of the response of stars to mass removal in different evolutionary stages and at different rates. The response also depends on the mass of the star. While computational methods for such an analyses are elaborated [224, 225], calculations of respective grids of models with full-fledged evolutionary codes at the time of writing of this review were not completed.
3.6.2 “Alpha”-formalism
Formation of the common envelope and evolution of a binary inside the former is a 3D hydrodynamic
process that may also include nuclear reactions; and current understanding of the process as a whole, as
well as computer power, are not sufficient for a solution of the problem (see, for detailed discussion, [319]).
Therefore, the outcome of this stage is, most commonly, evaluated in a simplified way, based on the balance
of the binding energy of the stellar envelope and the binary orbital energy, following independent
suggestions of van den Heuvel [794], Tutukov and Yungelson [783*], and Webbink [825*] and commonly
named after the later author as “Webbink’s” or “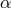 ”-formalism. The orbital evolution of the compact star
”-formalism. The orbital evolution of the compact star
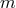 inside the envelope of the donor-star
inside the envelope of the donor-star 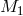 is driven by dynamic friction drag [553*]. This leads to a
gradual spiral-in process of the compact star. The above-mentioned energy condition may be written as
is driven by dynamic friction drag [553*]. This leads to a
gradual spiral-in process of the compact star. The above-mentioned energy condition may be written as
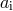 and
and 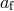 are the initial and final orbital separations,
are the initial and final orbital separations, 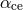 is the common envelope
parameter [783, 438] that describes the efficiency of expenditure of orbital energy on expulsion of the
envelope and
is the common envelope
parameter [783, 438] that describes the efficiency of expenditure of orbital energy on expulsion of the
envelope and 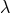 is a numerical coefficient that depends on the structure of the donor’s envelope,
introduced by de Kool et al. [138], and
is a numerical coefficient that depends on the structure of the donor’s envelope,
introduced by de Kool et al. [138], and 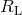 is the Roche lobe radius of the normal star that can be
approximated, e.g., by Eqs. (34*) or (35*). From Eq. (56*) one derives
where
is the Roche lobe radius of the normal star that can be
approximated, e.g., by Eqs. (34*) or (35*). From Eq. (56*) one derives
where 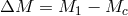 is the mass of the ejected envelope. For instance, the mass
is the mass of the ejected envelope. For instance, the mass 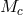 of the helium
core of a massive star can be approximated as [782*]
Then,
of the helium
core of a massive star can be approximated as [782*]
Then, 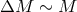 and, e.g., in the case of
and, e.g., in the case of 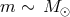 the orbital separation during the common envelope
stage can decrease by as much as a factor of 40 or even more.
the orbital separation during the common envelope
stage can decrease by as much as a factor of 40 or even more.
This treatment does not take into account possible transformations of the binary components during the
CE-stage. In addition, the pre-CE evolution of the binary components may be important for the onset and
the outcome of the CE, as calculations of synchronization of red giant stars in close binaries carried out by
Bear and Soker [29] indicate. The outcome of the common envelope stage is considered as a merger of
components if 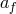 is such that the donor core comes into contact with the companion. Otherwise, it is
assumed that the core and companion form a detached system with the orbital separation
is such that the donor core comes into contact with the companion. Otherwise, it is
assumed that the core and companion form a detached system with the orbital separation 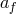 . Note an
important issue raised recently by Kashi and Soker [341]: while Eq. (57*) can formally imply that the
system becomes detached at the end of the CE stage, in fact, some matter of the envelope can not
reach the escape velocity and remains bound to the system and forms a circumbinary disk.
Angular momentum loss due to interaction with the disk may result in a further reduction of
binary separation and merger of components. This may influence the features of such stellar
populations as a close WD binary, hot subdwarfs, cataclysmic variables) and the rate of SN Ia (see
Section 7).
. Note an
important issue raised recently by Kashi and Soker [341]: while Eq. (57*) can formally imply that the
system becomes detached at the end of the CE stage, in fact, some matter of the envelope can not
reach the escape velocity and remains bound to the system and forms a circumbinary disk.
Angular momentum loss due to interaction with the disk may result in a further reduction of
binary separation and merger of components. This may influence the features of such stellar
populations as a close WD binary, hot subdwarfs, cataclysmic variables) and the rate of SN Ia (see
Section 7).
In the above equation for the common envelope, the outcome of the CE stage depends on the product of
two parameters: 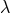 , which is the measure of the binding energy of the envelope to the core prior to the
mass transfer in a binary system, and
, which is the measure of the binding energy of the envelope to the core prior to the
mass transfer in a binary system, and 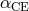 , which is the common envelope efficiency itself. Evaluation of
both parameters suffers from large physical uncertainties. For example, for
, which is the common envelope efficiency itself. Evaluation of
both parameters suffers from large physical uncertainties. For example, for  , the most debatable issues
are the accounting of the internal energy in the binding energy of the envelope and the definition of the
core/envelope boundary itself. Some authors argue (see e.g., [315]) that enthalpy rather than internal energy
should be included in the calculation of
, the most debatable issues
are the accounting of the internal energy in the binding energy of the envelope and the definition of the
core/envelope boundary itself. Some authors argue (see e.g., [315]) that enthalpy rather than internal energy
should be included in the calculation of  , which seems physically justifiable for convective
envelopes18.
We refer the interested reader to the detailed discussion in [139, 319].
, which seems physically justifiable for convective
envelopes18.
We refer the interested reader to the detailed discussion in [139, 319].
There exist several sets of fitting formulas for 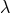 [856, 855] or binding energy of the envelopes
[446] based on detailed evolutionary computations for a range of stellar models at different
evolutionary stages. But we note, that in both studies the same specific evolutionary code ev [601] was
used and the core/envelope interface at location in the star with hydrogen abundance in the
hydrogen-burning shell
[856, 855] or binding energy of the envelopes
[446] based on detailed evolutionary computations for a range of stellar models at different
evolutionary stages. But we note, that in both studies the same specific evolutionary code ev [601] was
used and the core/envelope interface at location in the star with hydrogen abundance in the
hydrogen-burning shell 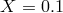 was assumed; in our opinion, the latter assumption is not justified
neither by any physical assumptions nor by evolutionary computations for Roche-lobe filling
stars. Even if the inaccuracy of the latter assumption is neglected, it is possible to use these
formulas only in population synthesis codes based on the evolutionary tracks obtained by ev
code.
was assumed; in our opinion, the latter assumption is not justified
neither by any physical assumptions nor by evolutionary computations for Roche-lobe filling
stars. Even if the inaccuracy of the latter assumption is neglected, it is possible to use these
formulas only in population synthesis codes based on the evolutionary tracks obtained by ev
code.
Our test calculations do not confirm the recent claim [313] that core/envelope interface, which also
defines the masses of the remnants in all cases of mass-exchange, is close to the radius of the sonic
velocity maximum in the hydrogen-burning shell of the mass-losing star at RLOF. As concerns
parameter 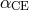 , the most critical issue is whether the sources other than orbital energy can
contribute to the energy balance, which include, in particular, recombination energy [724], nuclear
energy [299], or energy released by accretion onto the compact star. It should then be noted that
sometimes imposed to Eq. (56*) restriction
, the most critical issue is whether the sources other than orbital energy can
contribute to the energy balance, which include, in particular, recombination energy [724], nuclear
energy [299], or energy released by accretion onto the compact star. It should then be noted that
sometimes imposed to Eq. (56*) restriction 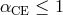 can not reflect the whole complexity of the
processes occurring in common envelopes. Although full-scale hydrodynamic calculations of a
common-envelope evolution exist, (see, e.g., [747, 140, 636, 637, 571] and references therein),
we stress again that the process is still very far from comprehension, especially, at the final
stages.
can not reflect the whole complexity of the
processes occurring in common envelopes. Although full-scale hydrodynamic calculations of a
common-envelope evolution exist, (see, e.g., [747, 140, 636, 637, 571] and references therein),
we stress again that the process is still very far from comprehension, especially, at the final
stages.
Actually, the state of the common envelope problem is currently such that it is possible only to estimate
the product 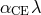 by modeling specific systems or well defined samples of objects corrected for
observational selection effects, like it is done in [765].
by modeling specific systems or well defined samples of objects corrected for
observational selection effects, like it is done in [765].
3.6.3 “Gamma”-formalism
Nelemans et. al. [517*] noted that the 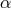 -formalism failed to reproduce parameters of several close
white dwarf binaries known circa 2000. In particular, for close helium white dwarf binaries with
known masses of both components, one can reconstruct the evolution of the system “back”
to the pair of main-sequence progenitors of components, since there is a unique relationship
between the mass of a white dwarf and the radius of its red giant progenitor [631], which is
almost independent of the total mass of the star. Formation of close white dwarf binaries should
definitely involve a spiral-in phase in the common envelope during the second episode of mass loss
(i.e., from the red giant to the white dwarf remnant of the original primary in the system).
In observed systems, mass ratios of components tend to concentrate to
-formalism failed to reproduce parameters of several close
white dwarf binaries known circa 2000. In particular, for close helium white dwarf binaries with
known masses of both components, one can reconstruct the evolution of the system “back”
to the pair of main-sequence progenitors of components, since there is a unique relationship
between the mass of a white dwarf and the radius of its red giant progenitor [631], which is
almost independent of the total mass of the star. Formation of close white dwarf binaries should
definitely involve a spiral-in phase in the common envelope during the second episode of mass loss
(i.e., from the red giant to the white dwarf remnant of the original primary in the system).
In observed systems, mass ratios of components tend to concentrate to  .
This means, that, if the first stage of mass transfer occurred through a common envelope, the
separation of components did not reduce much, contrary to what is expected from Eq. (57*). The
values of
.
This means, that, if the first stage of mass transfer occurred through a common envelope, the
separation of components did not reduce much, contrary to what is expected from Eq. (57*). The
values of 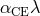 , which appeared necessary for reproducing the observed systems, turned out
to be negative, which means that the simple energy conservation law (57*) is violated in this
case. Instead, Nelemans et al. suggested that the first stage of mass exchange, between a giant
and a main-sequence star with comparable masses (
, which appeared necessary for reproducing the observed systems, turned out
to be negative, which means that the simple energy conservation law (57*) is violated in this
case. Instead, Nelemans et al. suggested that the first stage of mass exchange, between a giant
and a main-sequence star with comparable masses (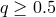 ), can be described by what they
called “
), can be described by what they
called “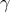 -formalism”, in which not the energy but the angular momentum
-formalism”, in which not the energy but the angular momentum 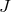 is balanced
and conservation of energy is implicitly implied, though formally this requires
is balanced
and conservation of energy is implicitly implied, though formally this requires 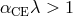 :
:
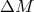 is the mass lost by the donor,
is the mass lost by the donor, 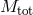 is the total mass of the binary system before formation of
the common envelope, and
is the total mass of the binary system before formation of
the common envelope, and  is a numerical coefficient. Similar conclusions were later reached by
Nelemans and Tout [516*] and van der Sluys et al. [803] who analyzed larger samples of binaries and used
detailed fits to evolutionary models instead of simple “core-mass – stellar radius” relation applied by
Nelemans et al. [517*]. It turned out that combination of
is a numerical coefficient. Similar conclusions were later reached by
Nelemans and Tout [516*] and van der Sluys et al. [803] who analyzed larger samples of binaries and used
detailed fits to evolutionary models instead of simple “core-mass – stellar radius” relation applied by
Nelemans et al. [517*]. It turned out that combination of 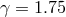 for the first stage of mass exchange
with
for the first stage of mass exchange
with 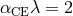 for the second episode of mass exchange enables, after taking into account selection effects,
a satisfactory model for population of close binary WD with known masses. In fact, findings of
Nelemans et al. and van der Sluys et al. confirmed the need for a loss of mass and momentum from
the system to explain observations of binaries mentioned in Section 3.3. (Note that
for the second episode of mass exchange enables, after taking into account selection effects,
a satisfactory model for population of close binary WD with known masses. In fact, findings of
Nelemans et al. and van der Sluys et al. confirmed the need for a loss of mass and momentum from
the system to explain observations of binaries mentioned in Section 3.3. (Note that 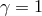 corresponds to the loss of the angular momentum by a fast stellar wind, which always increases the
orbital separation of the binary.) We stress that no physical process behind
corresponds to the loss of the angular momentum by a fast stellar wind, which always increases the
orbital separation of the binary.) We stress that no physical process behind 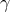 -formalism has
been suggested as yet, and the model remains purely phenomenological and should be further
investigated.19
-formalism has
been suggested as yet, and the model remains purely phenomenological and should be further
investigated.19
We should note that “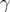 -formalism” was introduced under the assumption that stars with deep
convective envelopes (giants) always lose mass unstably, i.e., Ṁ is high. As mentioned above, if the mass
exchange is nonconservative, the associated angular momentum loss can increase the specific orbital angular
momentum of the system
-formalism” was introduced under the assumption that stars with deep
convective envelopes (giants) always lose mass unstably, i.e., Ṁ is high. As mentioned above, if the mass
exchange is nonconservative, the associated angular momentum loss can increase the specific orbital angular
momentum of the system 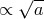 and hence the orbital separation
and hence the orbital separation  . Then the increasing Roche lobe can
accommodate the expanding donor, and the formation of a common envelope can be avoided. In fact, this
happens if part of the energy released by accretion is used to expel the matter from the vicinity of the
accretor (see, e.g., computations presented by King and Ritter [365], Beer et al. [30], Woods
et al. [849] who assumed that reemission occurs). It is not excluded that such nonconservative
mass-exchange with mass and momentum loss from the system may be the process underlying the
“
. Then the increasing Roche lobe can
accommodate the expanding donor, and the formation of a common envelope can be avoided. In fact, this
happens if part of the energy released by accretion is used to expel the matter from the vicinity of the
accretor (see, e.g., computations presented by King and Ritter [365], Beer et al. [30], Woods
et al. [849] who assumed that reemission occurs). It is not excluded that such nonconservative
mass-exchange with mass and momentum loss from the system may be the process underlying the
“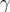 -formalism”.
-formalism”.
Nelemans and Tout [516], Zorotovic et al. [886] and De Marco et al. [139] attempted to estimate
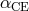 using samples of close WD + M-star binaries. It turned out that their formation can be explained
both if
using samples of close WD + M-star binaries. It turned out that their formation can be explained
both if 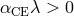 in Eq. (56*) or if
in Eq. (56*) or if 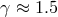 in Eq. (59*). This is sometimes considered as an argument
against the
in Eq. (59*). This is sometimes considered as an argument
against the 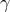 -formalism. But we note that in progenitors of WD + M-star binaries the companions to
giants are low-mass small-radius objects, which are quite different from
-formalism. But we note that in progenitors of WD + M-star binaries the companions to
giants are low-mass small-radius objects, which are quite different from 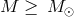 companions to WD
in progenitors of WD + WD binaries and, therefore, the energetics of the evolution in CE in
precursors of two types of systems can differ. In a recent population synthesis study of the
post-common-envelope binaries aimed at comparing to SDSS stars and taking into account selection effects,
Toonen and Nelemans [765] concluded that the best fit to the observations can be obtained
for small universal
companions to WD
in progenitors of WD + WD binaries and, therefore, the energetics of the evolution in CE in
precursors of two types of systems can differ. In a recent population synthesis study of the
post-common-envelope binaries aimed at comparing to SDSS stars and taking into account selection effects,
Toonen and Nelemans [765] concluded that the best fit to the observations can be obtained
for small universal  without the need to invoke the
without the need to invoke the 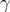 -formalism. However,
they also note that for almost equal mass precursors of WD binaries the widening of the orbit
in the course of mass transfer is needed (like in
-formalism. However,
they also note that for almost equal mass precursors of WD binaries the widening of the orbit
in the course of mass transfer is needed (like in 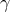 -formalism), while the formation of low
mass-ratio WD+M-star systems requires diminishing of the orbital separation (as suggested by
-formalism), while the formation of low
mass-ratio WD+M-star systems requires diminishing of the orbital separation (as suggested by
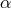 -formalism).
-formalism).
3.7 Other notes on the CE problem
A particular case of common envelopes (“double spiral-in”) occurs when both components are evolved. It was suggested [520*] that a common envelope is formed by the envelopes of both components of the system and the binding energy of them both should be taken into account, i.e., the outcome of CE must be found from a solution of an equation
Formulations of the common envelope equation different from Eq. (56*) are found in the literature (see,
e.g., [139] for a review); 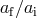 similar to the values produced by Eq. (56*) are then obtained for different
similar to the values produced by Eq. (56*) are then obtained for different
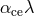 values.
values.
Common envelope events are expected to be rare (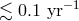 [791*]) and short-lasting
(
[791*]) and short-lasting
( years). Thus, the binaries at the CE-stage itself are difficult to observe, despite energy being
released at this stage comparable to the binding energy of a star, and the evidence for them
comes from the very existence of compact object binaries, as described above in Section 3.6.1.
Recently, it was suggested that luminous red transients – the objects with peak luminosity
intermediate between the brightest Novae and SN Ia (see, e.g., [342]) – can be associated with CE
[316, 792].
years). Thus, the binaries at the CE-stage itself are difficult to observe, despite energy being
released at this stage comparable to the binding energy of a star, and the evidence for them
comes from the very existence of compact object binaries, as described above in Section 3.6.1.
Recently, it was suggested that luminous red transients – the objects with peak luminosity
intermediate between the brightest Novae and SN Ia (see, e.g., [342]) – can be associated with CE
[316, 792].
We recall also that the stability and timescale of mass-exchange in a binary depends on the mass ratio of
components 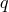 , the structure of the envelope of the Roche-lobe filling star, and possible stabilizing effects
of mass and momentum loss from the system [780, 283, 873*, 261, 268*, 318*, 196, 76, 849]. We note
especially recent claims [848, 570] that the local thermal timescale of the super-adiabatic layer existing over
a convective envelope of giants may be shorter than the donor’s dynamic timescale. As a result, giants may
adjust to a high mass loss and retain their radii or even contract (instead of dramatically expanding, as
expected in the adiabatic approximation [224, 225]). As well, the response of stars to mass loss evolves in
the course of the latter depending on whether the super-adiabatic layer may be removed. The recent
discovery of young helium WD companions to blue stragglers in wide binaries (
, the structure of the envelope of the Roche-lobe filling star, and possible stabilizing effects
of mass and momentum loss from the system [780, 283, 873*, 261, 268*, 318*, 196, 76, 849]. We note
especially recent claims [848, 570] that the local thermal timescale of the super-adiabatic layer existing over
a convective envelope of giants may be shorter than the donor’s dynamic timescale. As a result, giants may
adjust to a high mass loss and retain their radii or even contract (instead of dramatically expanding, as
expected in the adiabatic approximation [224, 225]). As well, the response of stars to mass loss evolves in
the course of the latter depending on whether the super-adiabatic layer may be removed. The recent
discovery of young helium WD companions to blue stragglers in wide binaries (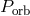 from 120 to
3010 days) in open cluster NGC 188 [248] supports the idea that in certain cases
RLOF in wide systems may be stable. These considerations, which need further systematic
exploration, may change the “standard” paradigm of the stability of mass exchange formulated in this
section.
from 120 to
3010 days) in open cluster NGC 188 [248] supports the idea that in certain cases
RLOF in wide systems may be stable. These considerations, which need further systematic
exploration, may change the “standard” paradigm of the stability of mass exchange formulated in this
section.






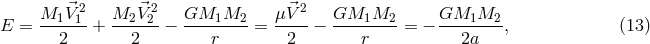
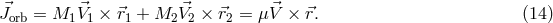



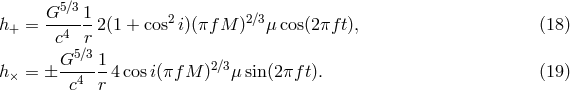
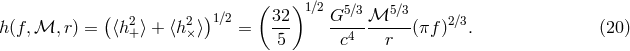
![3 [( )2 ( )2] -dE---≡ F = --c--- ∂h+- + ∂h×- . (21 ) dA dt 16πG ∂t ∂t](article249x.gif)


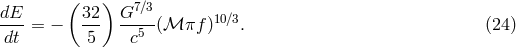


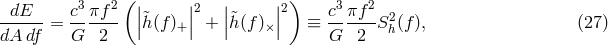

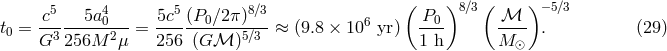
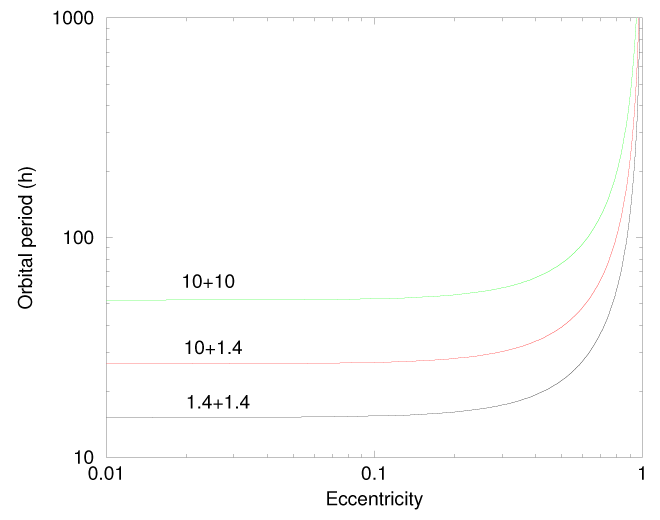
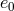 . The lines are calculated for
. The lines are calculated for 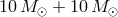 (BH + BH),
(BH + BH),  (BH + NS), and
(BH + NS), and 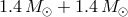 (NS + NS).
(NS + NS).
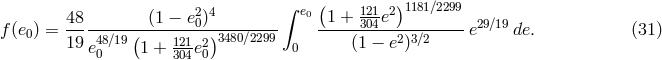
![˙ −28 2 −2 −2 2 4 3 JMSW = − 0.5 × 10 [g cm s ]λ k M2R 2ω , (32 )](article302x.gif)
![GM1 GM2 1 2 [ 2 2] Φ = − --2----2----21∕2 − --------2---2----2-1∕2-− --Ωorb (x − μa ) + y , (33 ) [x + y + z ] [(x − a ) + y + z ] 2](article319x.gif)
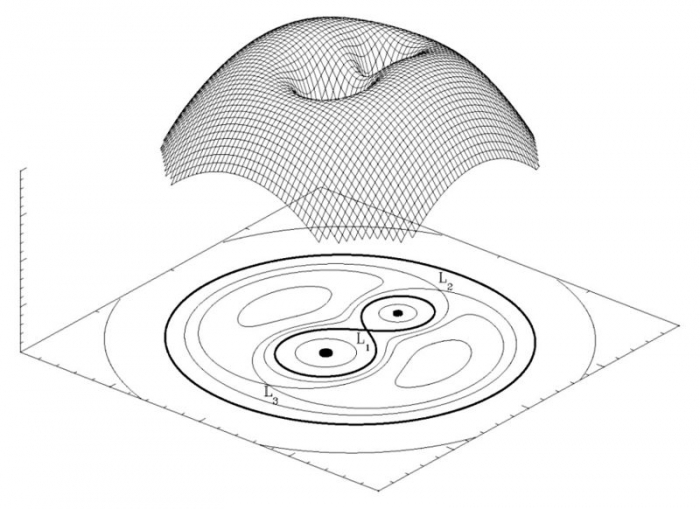
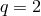 .
. 

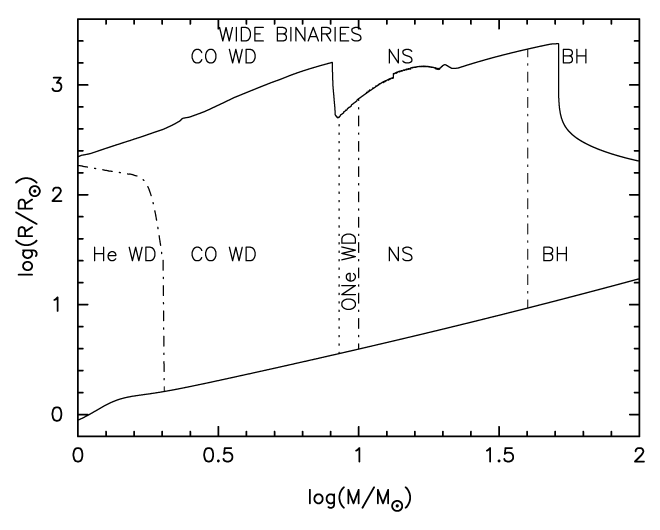
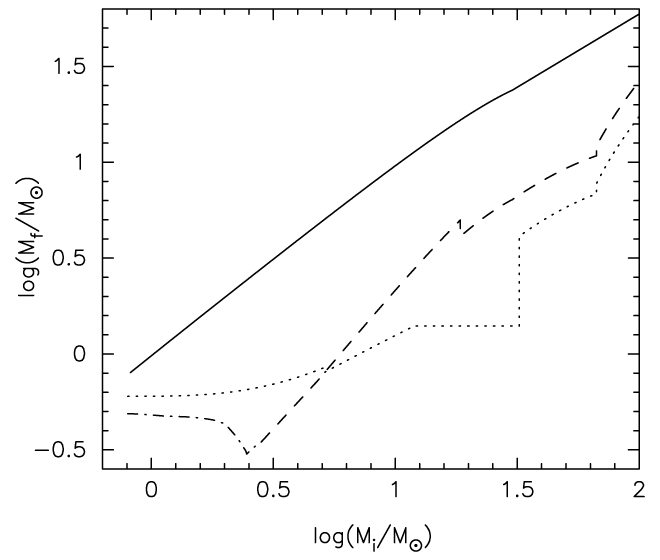
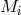 and their masses at TAMS (solid line),
masses of helium stars (dashed line), masses of He WD (dash-dotted line), masses of CO and ONe
WD (dotted line). For stars with
and their masses at TAMS (solid line),
masses of helium stars (dashed line), masses of He WD (dash-dotted line), masses of CO and ONe
WD (dotted line). For stars with  we plot the upper limit of WD masses for case
we plot the upper limit of WD masses for case 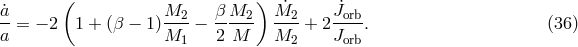






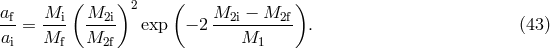
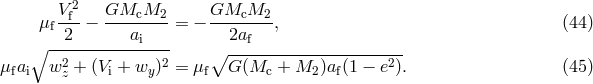
![[ ( )] −1 af w2x +-w2z +-(Vi +-wy-)2 a = 2 − χ V 2 (46 ) i i](article423x.gif)