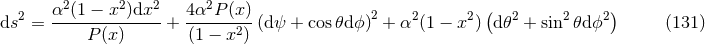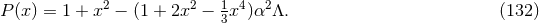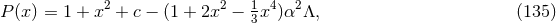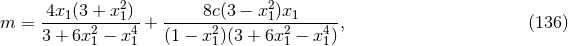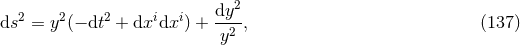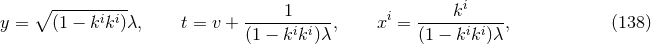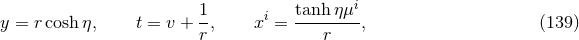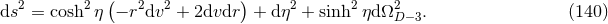7 Applications and Related Topics
7.1 Black-hole uniqueness theorems
One of the main motivations for classifying near-horizon geometries is to prove uniqueness theorems for the corresponding extremal black-hole solutions. This turns out to be a much harder problem and has only been achieved when extra structure is present that constrains certain global aspects of the spacetime. The role of the near-horizon geometry is to provide the correct boundary conditions near the horizon for the global–black-hole solution.
7.1.1 Supersymmetric black holes
Uniqueness theorems for supersymmetric black holes have been proved in the simplest four and five-dimensional supergravity theories, by employing the associated near-horizon classifications described in Section 5.
In four dimensions, the simplest supergravity theory that admits supersymmetric black holes is 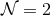 minimal supergravity; its bosonic sector is simply Einstein–Maxwell theory.
minimal supergravity; its bosonic sector is simply Einstein–Maxwell theory.
Theorem 7.1 ([41]). Consider an asymptotically-flat, supersymmetric black-hole solution to
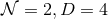 minimal supergravity. Assume that the supersymmetric Killing vector field is timelike
everywhere outside the horizon. Then it must belong to the Majumdar–Papapetrou family of black
holes. If the horizon is connected it must be the extremal RN black hole.
minimal supergravity. Assume that the supersymmetric Killing vector field is timelike
everywhere outside the horizon. Then it must belong to the Majumdar–Papapetrou family of black
holes. If the horizon is connected it must be the extremal RN black hole.
It would be interesting to remove the assumption on the supersymmetric Killing vector field to provide a complete classification of supersymmetric black holes in this case.
In five dimensions, the simplest supergravity theory that admits supersymmetric black holes is 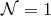 minimal supergravity. Using general properties of supersymmetric solutions in this theory, as well as the
near-horizon classification discussed in Section 5, the following uniqueness theorem has been
obtained.
minimal supergravity. Using general properties of supersymmetric solutions in this theory, as well as the
near-horizon classification discussed in Section 5, the following uniqueness theorem has been
obtained.
Theorem 7.2 ([191]). Consider an asymptotically-flat, supersymmetric black-hole solution to
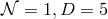 minimal supergravity, with horizon cross section
minimal supergravity, with horizon cross section 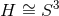 . Assume that the
supersymmetric Killing vector field is timelike everywhere outside the horizon. Then it must belong
to the BMPV family of black holes [30].
. Assume that the
supersymmetric Killing vector field is timelike everywhere outside the horizon. Then it must belong
to the BMPV family of black holes [30].
Remarks:
- The BMPV solution is a stationary, non-static, non-rotating black hole with angular momentum
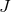 and electric charge
and electric charge 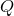 . For
. For 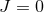 it reduces to the extremal RN black hole.
it reduces to the extremal RN black hole.
- It would be interesting to investigate the classification of supersymmetric black holes without the assumption on the supersymmetric Killing vector field.
- An analogous uniqueness theorem for supersymmetric black rings [66], i.e., for
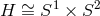 ,
remains an open problem.
,
remains an open problem.
- An analogous result has been obtained for minimal supergravity theory coupled to an arbitrary number of vector multiplets [111].
Analogous results for asymptotically AdS black holes in gauged supergravity have yet-to-be-obtained and this
remains a very interesting open problem. This is particularly significant due to the lack of black-hole
uniqueness theorems even for pure gravity in AdS. However, it is worth mentioning that the analysis
of [120] used the homogeneous near-horizon geometry of Theorem 5.3 with 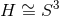 , together with
supersymmetry, to explicitly integrate for the full cohomogeneity-1 AdS5 black hole solution. It would be
interesting to prove a uniqueness theorem for supersymmetric AdS5 black holes assuming
, together with
supersymmetry, to explicitly integrate for the full cohomogeneity-1 AdS5 black hole solution. It would be
interesting to prove a uniqueness theorem for supersymmetric AdS5 black holes assuming 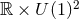 symmetry.
symmetry.
7.1.2 Extremal vacuum black holes
The classic black-hole uniqueness theorem of general relativity roughly states that any stationary, asymptotically-flat black-hole solution to the vacuum Einstein equations must be given by the Kerr solution. Traditionally this theorem assumed that the event horizon is non-degenerate, at a number of key steps. Most notably, the rigidity theorem, which states that a stationary rotating black hole must be axisymmetric, is proved by first showing that the event horizon is a Killing horizon. Although the original arguments [127] assumed non-degeneracy of the horizon, in four dimensions this assumption can be removed [179, 180, 134].
This allows one to reduce the problem to a boundary value problem on a two-dimensional domain (the orbit space), just as in the case of a non-degenerate horizon. However, the boundary conditions near the boundary corresponding to the horizon depend on whether the surface gravity vanishes or not. Unsurprisingly, the boundary conditions near a degenerate horizon can be deduced from the near-horizon geometry. Curiously, this has only been realised rather recently. This has allowed one to extend the uniqueness theorem for Kerr to the degenerate case.
Theorem 7.3 ([178 , 5
, 5 , 80
, 80 , 40
, 40 ]). The only four-dimensional, asymptotically-flat, stationary and
axisymmetric, rotating, black-hole solution of the Einstein vacuum equations, with a connected
degenerate horizon with non-toroidal horizon sections, is the extremal Kerr solution.
]). The only four-dimensional, asymptotically-flat, stationary and
axisymmetric, rotating, black-hole solution of the Einstein vacuum equations, with a connected
degenerate horizon with non-toroidal horizon sections, is the extremal Kerr solution.
We note that [178] employs methods from integrability and the inverse scattering method. The remaining proofs employ the near-horizon geometry classification theorem discussed in Section 4.3 together with the standard method used to prove uniqueness of non-extremal Kerr. The above uniqueness theorem has also been established for the extremal Kerr–Newman black hole in Einstein–Maxwell theory [5, 40, 177].
The assumption of a non-toroidal horizon is justified by the black-hole–horizon topology theorems. Similarly, as discussed above, axisymmetry is justified by the rigidity theorem under the assumption of analyticity. Together with these results, the above theorem provides a complete classification of rotating vacuum black holes with a single degenerate horizon, under the stated assumptions. The proof that a non-rotating black hole must be static has only been established for non-degenerate horizons, so the classification of non-rotating degenerate black holes remains an open problem.
Of course, in higher dimensions, there is no such simple general uniqueness theorem. For spacetimes with
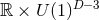 symmetry though, one has a mathematical structure analogous to
symmetry though, one has a mathematical structure analogous to 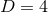 stationary and
axisymmetric spacetimes. Namely, one can reduce the problem to an integrable boundary-value problem on
a 2D orbit space. However in this case the boundary data is more complicated. It was first
shown that non-degenerate black-hole solutions in this class are uniquely specified by certain
topological data, which specifies the
stationary and
axisymmetric spacetimes. Namely, one can reduce the problem to an integrable boundary-value problem on
a 2D orbit space. However in this case the boundary data is more complicated. It was first
shown that non-degenerate black-hole solutions in this class are uniquely specified by certain
topological data, which specifies the 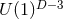 -action on the manifold, referred to as interval
data (i.e., rod structure) [138, 139]. The proof is entirely analogous to that for uniqueness of
Kerr amongst stationary and axisymmetric black holes. This has been extended to cover the
degenerate case, again by employing the near-horizon geometry to determine the correct boundary
conditions.
-action on the manifold, referred to as interval
data (i.e., rod structure) [138, 139]. The proof is entirely analogous to that for uniqueness of
Kerr amongst stationary and axisymmetric black holes. This has been extended to cover the
degenerate case, again by employing the near-horizon geometry to determine the correct boundary
conditions.
Proposition 7.1 ([80]). Consider a five-dimensional, asymptotically-flat, stationary black-hole
solution of the vacuum Einstein equations, with 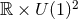 isometry group and a connected
degenerate horizon (with non-toroidal sections). There exists at most one such solution with given
angular momenta and a given interval structure.
isometry group and a connected
degenerate horizon (with non-toroidal sections). There exists at most one such solution with given
angular momenta and a given interval structure.
It is worth emphasising that although there is no near-horizon uniqueness theorem in this case, see
Section 4.4, this result actually only requires the general 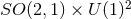 form for the near-horizon
geometry and not its detailed functional form.
form for the near-horizon
geometry and not its detailed functional form.
It seems likely that the results of this section could be extended to 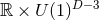 invariant extremal
black holes in Einstein–Maxwell type theories in higher dimensions. In
invariant extremal
black holes in Einstein–Maxwell type theories in higher dimensions. In 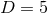 it is known
that coupling a CS term in such a way to give the bosonic sector of minimal supergravity,
implies such solutions are determined by a non-linear sigma model analogous to the pure vacuum
case. Hence it should be straightforward to generalise the vacuum uniqueness theorems to this
theory.
it is known
that coupling a CS term in such a way to give the bosonic sector of minimal supergravity,
implies such solutions are determined by a non-linear sigma model analogous to the pure vacuum
case. Hence it should be straightforward to generalise the vacuum uniqueness theorems to this
theory.
7.2 Stability of near-horizon geometries and extremal black holes
All known near-horizon geometries are fibrations of the horizon cross section 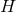 over an AdS2 base (see
Section 3.2). By writing the AdS2 in global coordinates one obtains examples of smooth complete
spacetimes that solve the Einstein equations. Explicitly, by converting the near-horizon geometry (65
over an AdS2 base (see
Section 3.2). By writing the AdS2 in global coordinates one obtains examples of smooth complete
spacetimes that solve the Einstein equations. Explicitly, by converting the near-horizon geometry (65 ) to
AdS2 global coordinates, such spacetimes take the general form
) to
AdS2 global coordinates, such spacetimes take the general form
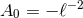 in terms of the radius of AdS
2. These spacetimes possess
two timelike boundaries, and of course do not contain a horizon. It is of interest to consider the stability of
such “global” near-horizon geometries, as spacetimes in their own right. It turns out that this problem is
rather subtle.
in terms of the radius of AdS
2. These spacetimes possess
two timelike boundaries, and of course do not contain a horizon. It is of interest to consider the stability of
such “global” near-horizon geometries, as spacetimes in their own right. It turns out that this problem is
rather subtle.
In fact, general arguments suggest that any near-horizon geometry must be unstable when backreaction
is taken into account and the nearby solution must be singular [18 ]. This follows from the fact
that
]. This follows from the fact
that 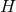 is marginally trapped, so there exist perturbations that create a trapped surface and
by the singularity theorems the resulting spacetime must be geodesically incomplete. If the
perturbed solution is a black hole sitting inside the near-horizon geometry, then this need not be an
issue.21
For
is marginally trapped, so there exist perturbations that create a trapped surface and
by the singularity theorems the resulting spacetime must be geodesically incomplete. If the
perturbed solution is a black hole sitting inside the near-horizon geometry, then this need not be an
issue.21
For 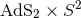 , heuristic arguments also indicating its instability have been obtained by
dimensional reduction to an AdS2 theory of gravity [170]. In particular, this suggests that the
backreaction of matter in
, heuristic arguments also indicating its instability have been obtained by
dimensional reduction to an AdS2 theory of gravity [170]. In particular, this suggests that the
backreaction of matter in 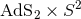 , is not consistent with a fall-off preserving both of the AdS
2
boundaries.
, is not consistent with a fall-off preserving both of the AdS
2
boundaries.
So far we have been talking about the non-linear stability of near-horizon geometries. Of course,
linearised perturbations in these backgrounds can be analysed in more detail. A massless scalar field in the
near-horizon geometry of an extremal Kerr black hole (NHEK) reduces to a massive charged scalar field in
AdS2 with a homogeneous electric field [18]. This turns out to capture the main features of the Teukolsky
equation for NHEK, which describes linearised gravitational perturbations of NHEK [4 , 60]. In contrast to
the above instability, these works revealed the stability of NHEK against linearised gravitational
perturbations. In fact, one can prove a non-linear uniqueness theorem in this context: any stationary and
axisymmetric solution that is asymptotic to NHEK, possibly containing a smooth horizon, must in fact be
NHEK [4].
, 60]. In contrast to
the above instability, these works revealed the stability of NHEK against linearised gravitational
perturbations. In fact, one can prove a non-linear uniqueness theorem in this context: any stationary and
axisymmetric solution that is asymptotic to NHEK, possibly containing a smooth horizon, must in fact be
NHEK [4].
So far we have discussed the stability of near-horizon geometries as spacetimes in their own right. A
natural question is what information about the stability of an extremal black hole can be deduced
from the stability properties of its near horizon geometry. Clearly, stability of the near-horizon
geometry is insufficient to establish stability of the black hole, but it has been argued that
certain instabilities of the near-horizon geometry imply instability of the black hole [62 ]. For
higher dimensional vacuum near-horizon geometries, one can construct gauge-invariant quantities
(Weyl scalars), whose perturbation equations decouple, generalising the Teukolsky equation
[62
]. For
higher dimensional vacuum near-horizon geometries, one can construct gauge-invariant quantities
(Weyl scalars), whose perturbation equations decouple, generalising the Teukolsky equation
[62 ].22
One can then perform a KK reduction on
].22
One can then perform a KK reduction on 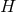 to find that linearised gravitational (and electromagnetic)
perturbations reduce to an equation for a massive charged scalar field in AdS2 with a homogeneous electric
field (as for the NHEK case above). The authors of [62] define the near-horizon geometry to be unstable if
the effective Breitenlohner–Freedman bound for this charged scalar field is violated. They propose the
following conjecture: an instability of the near-horizon geometry (in the above sense), implies an instability
of the associated extreme black hole, provided the unstable mode satisfies a certain symmetry requirement.
This conjecture is supported by the linear stability of NHEK and was verified for the known instabilities of
odd dimensional cohomogeneity-1 MP black holes [57]. It is also supported by the known stability results
for the five-dimensional MP black hole [181] and the Kerr-AdS4 black hole [61]. This conjecture suggests
that even-dimensional near-extremal MP black holes, which are more difficult to analyse directly, are also
unstable [203].
to find that linearised gravitational (and electromagnetic)
perturbations reduce to an equation for a massive charged scalar field in AdS2 with a homogeneous electric
field (as for the NHEK case above). The authors of [62] define the near-horizon geometry to be unstable if
the effective Breitenlohner–Freedman bound for this charged scalar field is violated. They propose the
following conjecture: an instability of the near-horizon geometry (in the above sense), implies an instability
of the associated extreme black hole, provided the unstable mode satisfies a certain symmetry requirement.
This conjecture is supported by the linear stability of NHEK and was verified for the known instabilities of
odd dimensional cohomogeneity-1 MP black holes [57]. It is also supported by the known stability results
for the five-dimensional MP black hole [181] and the Kerr-AdS4 black hole [61]. This conjecture suggests
that even-dimensional near-extremal MP black holes, which are more difficult to analyse directly, are also
unstable [203].
Recently, it has been shown that extremal black holes exhibit linearised instabilities at the
horizon. This was first observed for a massless scalar field in an extremal RN and extremal
Kerr–black-hole background [8, 7, 6, 9]. The instability is somewhat subtle. While the scalar decays
everywhere on and outside the horizon, the first transverse derivative of the scalar does not
generically decay on the horizon, and furthermore the 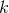 th-transverse derivative blows up as
th-transverse derivative blows up as
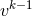 along the horizon. These results follow from the existence of a non-vanishing conserved
quantity on the horizon linear in the scalar field. If the conserved quantity vanishes it has been
shown that a similar, albeit milder, instability still occurs on the horizon [54, 26, 11, 167
along the horizon. These results follow from the existence of a non-vanishing conserved
quantity on the horizon linear in the scalar field. If the conserved quantity vanishes it has been
shown that a similar, albeit milder, instability still occurs on the horizon [54, 26, 11, 167 ]. It
should be noted that this instability is not in contradiction with the above linear stability of the
near-horizon geometry. From the point of view of the near-horizon geometry, it is merely a
coordinate artefact corresponding to the fact that the Poincaré horizon of AdS2 is not invariantly
defined [167].
]. It
should be noted that this instability is not in contradiction with the above linear stability of the
near-horizon geometry. From the point of view of the near-horizon geometry, it is merely a
coordinate artefact corresponding to the fact that the Poincaré horizon of AdS2 is not invariantly
defined [167].
The horizon instability has been generalised to a massless scalar in an arbitrary extremal black hole in
any dimension, provided the near-horizon geometry satisfies a certain assumption [168 ]. This assumption in
fact follows from the AdS2-symmetry theorems and hence is satisfied by all known extremal black holes.
Furthermore, by considering the Teukolsky equation, it was shown that a similar horizon instability occurs
for linearised gravitational perturbations of extremal Kerr [168
]. This assumption in
fact follows from the AdS2-symmetry theorems and hence is satisfied by all known extremal black holes.
Furthermore, by considering the Teukolsky equation, it was shown that a similar horizon instability occurs
for linearised gravitational perturbations of extremal Kerr [168 ]. This was generalised to certain
higher-dimensional vacuum extremal black holes [182]. Similarly, using Moncrief’s perturbation
formalism for RN, it was shown that coupled gravitational and electromagnetic perturbations
of extremal RN within Einstein–Maxwell theory also exhibit such a horizon instability [168].
An interesting open question is what is the fate of the non-linear evolution of such horizon
instabilities. To this end, an analogous instability has been established for certain non-linear wave
equations [10].
]. This was generalised to certain
higher-dimensional vacuum extremal black holes [182]. Similarly, using Moncrief’s perturbation
formalism for RN, it was shown that coupled gravitational and electromagnetic perturbations
of extremal RN within Einstein–Maxwell theory also exhibit such a horizon instability [168].
An interesting open question is what is the fate of the non-linear evolution of such horizon
instabilities. To this end, an analogous instability has been established for certain non-linear wave
equations [10].
7.3 Geometric inequalities
Interestingly, near-horizon geometries saturate certain geometric bounds relating the area and conserved angular momentum and charge of dynamical axisymmetric horizons, see [53] for a review.
In particular, for four-dimensional dynamical axially-symmetric spacetimes, the area of black-hole horizons with a given angular momentum is minimised by the extremal Kerr black hole. The precise statement is:
Theorem 7.4 ([55, 143]). Consider a spacetime satisfying the Einstein equations with a non-negative
cosmological constant and matter obeying the dominant energy condition. The area of any axisymmetric
closed (stably outermost) marginally–outer-trapped surface 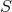 satisfies
satisfies
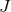 is the angular momentum of
is the angular momentum of 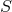 . Furthermore, this bound is saturated if and only if
the metric induced on
. Furthermore, this bound is saturated if and only if
the metric induced on 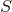 is that of the (near-)horizon geometry of an extreme Kerr black
hole.
is that of the (near-)horizon geometry of an extreme Kerr black
hole.
Furthermore, it has been shown that if 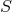 is a section of an isolated horizon the above equality is
saturated if and only if the surface gravity vanishes [142] (see also [172]). An analogous area-angular
momentum-charge inequality has been derived in Einstein–Maxwell theory, which is saturated by the
extreme Kerr–Newman black hole [87].
is a section of an isolated horizon the above equality is
saturated if and only if the surface gravity vanishes [142] (see also [172]). An analogous area-angular
momentum-charge inequality has been derived in Einstein–Maxwell theory, which is saturated by the
extreme Kerr–Newman black hole [87].
The above result can be generalised to higher dimensions, albeit under stronger symmetry assumptions.
Theorem 7.5 ([132]). Consider a 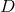 -dimensional spacetime satisfying the vacuum Einstein
equations with non-negative cosmological constant
-dimensional spacetime satisfying the vacuum Einstein
equations with non-negative cosmological constant 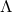 that admits a
that admits a 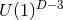 -rotational isometry.
Then the area of any (stably outer) marginally–outer-trapped surface satisfies
-rotational isometry.
Then the area of any (stably outer) marginally–outer-trapped surface satisfies 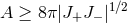 where
where 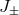 are distinguished components of the angular momenta associated to the rotational Killing
fields, which have fixed points on the horizon. Further, if
are distinguished components of the angular momenta associated to the rotational Killing
fields, which have fixed points on the horizon. Further, if 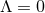 then equality is achieved if the
spacetime is a near-horizon geometry and conversely, if the bound is saturated, the induced geometry
on spatial cross sections of the horizon is that of a near-horizon geometry.
then equality is achieved if the
spacetime is a near-horizon geometry and conversely, if the bound is saturated, the induced geometry
on spatial cross sections of the horizon is that of a near-horizon geometry.
In particular, for 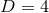 , the horizon is topologically
, the horizon is topologically 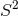 and
and 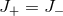 and one recovers
(130
and one recovers
(130 ).
).
Other generalisations of such inequalities have been obtained in  Einstein–Maxwell-dilaton
theories [210, 211].
Einstein–Maxwell-dilaton
theories [210, 211].
The proof of the above results involve demonstrating that axisymmetric near-horizon geometries are
global minimisers of a functional of the form (128 ) that is essentially the energy of a harmonic map, as
discussed in Section 6.4.
) that is essentially the energy of a harmonic map, as
discussed in Section 6.4.
7.4 Analytic continuation
In this section we discuss analytic continuation of near-horizon geometries to obtain other Lorentzian or Riemannian metrics. As we will see, this uncovers a number of surprising connections between seemingly different spacetimes and geometries.
As discussed in Section 3.2, typically near-horizon geometries have an 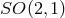 isometry. Generically,
the orbits of this isometry are three-dimensional line or circle bundles over AdS2. One can often analytically
continue these geometries so
isometry. Generically,
the orbits of this isometry are three-dimensional line or circle bundles over AdS2. One can often analytically
continue these geometries so 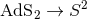 and
and 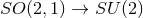 (or
(or 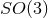 ) with orbits that are
circle bundles over
) with orbits that are
circle bundles over 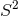 . It is most natural to work with the near-horizon geometry written in global AdS
2
coordinates (129
. It is most natural to work with the near-horizon geometry written in global AdS
2
coordinates (129 ). Such analytic continuations are then obtained by setting
). Such analytic continuations are then obtained by setting 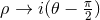 and
and
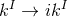 .
.
First we discuss four dimensions. One can perform an analytic continuation of the near-horizon
geometry of extremal Kerr to obtain the zero mass Lorentzian Taub–NUT solution [162 ]. More generally,
there is an analytic continuation of the near-horizon geometry of extremal Kerr–Newman-
]. More generally,
there is an analytic continuation of the near-horizon geometry of extremal Kerr–Newman-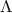 to the zero
mass Lorentzian RN–Taub–NUT-
to the zero
mass Lorentzian RN–Taub–NUT-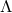 solution [154]. In fact, Page constructed a smooth compact
Riemannian metric on the non-trivial
solution [154]. In fact, Page constructed a smooth compact
Riemannian metric on the non-trivial 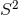 -bundle over
-bundle over 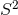 with
with 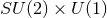 isometry, by taking
a certain limit of the Euclidean Kerr-dS metric [185]. He showed that locally his metric is
the Euclidean Taub–NUT-
isometry, by taking
a certain limit of the Euclidean Kerr-dS metric [185]. He showed that locally his metric is
the Euclidean Taub–NUT-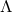 with zero mass. Hence, it follows that there exists an analytic
continuation of the near-horizon geometry of extremal Kerr-
with zero mass. Hence, it follows that there exists an analytic
continuation of the near-horizon geometry of extremal Kerr-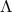 to Page’s Einstein manifold. (Also we
deduce that Page’s limit is a Riemannian version of a combined extremal and near-horizon
limit).
to Page’s Einstein manifold. (Also we
deduce that Page’s limit is a Riemannian version of a combined extremal and near-horizon
limit).
Explicitly, the analytic continuation of the near-horizon extremal Kerr-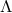 metric (83
metric (83 ) to the Page
metric, can be obtained as follows. First write the near-horizon geometry in global coordinates (129
) to the Page
metric, can be obtained as follows. First write the near-horizon geometry in global coordinates (129 ), then
analytically continue
), then
analytically continue 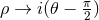 and
and 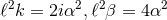 and redefine the coordinates
and redefine the coordinates
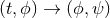 appropriately, to find
appropriately, to find
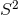 bundle over
bundle over 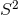 , as follows. Compactness and positive definiteness requires
one to take
, as follows. Compactness and positive definiteness requires
one to take 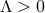 and
and 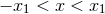 where
where 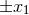 are two adjacent roots of
are two adjacent roots of 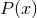 such that
such that
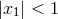 . The
. The 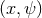 part of the metric has conical singularities at
part of the metric has conical singularities at 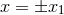 , which are removed by
imposing
resulting in an
, which are removed by
imposing
resulting in an 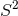 fibre. This fibration is globally defined if
fibre. This fibration is globally defined if 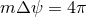 , where
, where 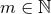 , so combining
these results implies
As Page showed, the only solution is
, so combining
these results implies
As Page showed, the only solution is 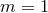 , which implies the
, which implies the 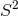 -bundle is non-trivial. This manifold is
diffeomorphic to the first del Pezzo surface
-bundle is non-trivial. This manifold is
diffeomorphic to the first del Pezzo surface 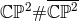 .
.
Similarly, there is an analytic continuation of the near-horizon geometry of the extremal
Kerr–Newman-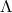 that gives a family of smooth Riemannian metrics on
that gives a family of smooth Riemannian metrics on 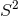 -bundles over
-bundles over 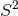 that
satisfy the Riemannian Einstein–Maxwell equations (and hence have constant scalar curvature).
Interestingly, this leads to an infinite class of metrics (i.e., there are an infinite number of possibilities for
the integer
that
satisfy the Riemannian Einstein–Maxwell equations (and hence have constant scalar curvature).
Interestingly, this leads to an infinite class of metrics (i.e., there are an infinite number of possibilities for
the integer 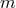 ). The local solution can be derived directly by classifying solutions of the Riemannian
Einstein–Maxwell equations with
). The local solution can be derived directly by classifying solutions of the Riemannian
Einstein–Maxwell equations with 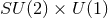 isometry group acting on three-dimensional
orbits (see, e.g., [173]). One finds the geometry is given by (131
isometry group acting on three-dimensional
orbits (see, e.g., [173]). One finds the geometry is given by (131 ) but with
) but with 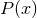 now given by
now given by
 is a constant related to the electric and magnetic charges of the analytically continued extremal
Kerr–Newmann black hole. The regularity condition now becomes
which for
is a constant related to the electric and magnetic charges of the analytically continued extremal
Kerr–Newmann black hole. The regularity condition now becomes
which for 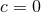 reduces to Eq. (134
reduces to Eq. (134 ). One can check the 2nd term above is monotonically
increasing in the range
). One can check the 2nd term above is monotonically
increasing in the range 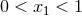 and unbounded as
and unbounded as 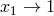 . If
. If 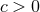 then there is a unique
solution for every integer
then there is a unique
solution for every integer 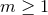 . For
. For 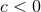 the only allowed solution is
the only allowed solution is 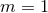 , and in
fact there exist values of
, and in
fact there exist values of 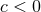 such that there are two solutions with
such that there are two solutions with 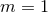 . For
. For 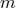 even, the metric extends to a global metric on the trivial
even, the metric extends to a global metric on the trivial 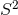 bundle over
bundle over 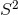 , whereas for
, whereas for
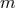 odd, globally the space is
odd, globally the space is 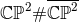 . Hence one obtains a generalisation of the Page
metric.
. Hence one obtains a generalisation of the Page
metric.
Curiously, in five dimensions there exist analytic continuations of near-horizon geometries to stationary
black-hole solutions [162]. For example, one can perform an analytic continuation of the near-horizon
geometry of an extremal MP black hole with 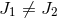 to obtain the full cohomogeneity-1 MP black hole
with
to obtain the full cohomogeneity-1 MP black hole
with 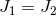 (which need not be extremal). In this case the
(which need not be extremal). In this case the 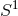 bundle over
bundle over 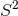 that results
after analytic continuation is the homogenous
that results
after analytic continuation is the homogenous 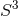 of the resulting black hole. This generalises
straightforwardly with the addition of a cosmological constant and/or charge. Interestingly, this also works
with the near-horizon geometries of extremal black rings. For example, there is an analytic
continuation of the near-horizon geometry of the extremal dipole black ring that gives a static
charged squashed KK black hole with
of the resulting black hole. This generalises
straightforwardly with the addition of a cosmological constant and/or charge. Interestingly, this also works
with the near-horizon geometries of extremal black rings. For example, there is an analytic
continuation of the near-horizon geometry of the extremal dipole black ring that gives a static
charged squashed KK black hole with 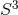 horizon topology. In these five-dimensional cases,
the isometry of the near-horizon geometries is
horizon topology. In these five-dimensional cases,
the isometry of the near-horizon geometries is 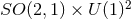 , which has 4D orbits; hence
one can arrange the new time coordinate to lie in these orbits in such a way it is not acted
upon by the
, which has 4D orbits; hence
one can arrange the new time coordinate to lie in these orbits in such a way it is not acted
upon by the 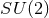 . This avoids NUT charge, which is inevitable in the four-dimensional case
discussed above. As in the four-dimensional case, there are analytic continuations which result in
Einstein metrics on compact manifolds. For example, there is an analytic continuation of the
near-horizon geometry of extremal MP-
. This avoids NUT charge, which is inevitable in the four-dimensional case
discussed above. As in the four-dimensional case, there are analytic continuations which result in
Einstein metrics on compact manifolds. For example, there is an analytic continuation of the
near-horizon geometry of extremal MP-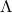 that gives an infinite class of Einstein metrics on
that gives an infinite class of Einstein metrics on
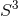 -bundles over
-bundles over 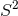 , which were first found by taking a Page limit of the MP-dS black
hole [126].
, which were first found by taking a Page limit of the MP-dS black
hole [126].
In higher than five dimensions one can similarly perform analytic continuations of Einstein near-horizon
geometries to obtain examples of compact Einstein manifolds. The near-horizon geometries of MP-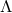 give
the Einstein manifolds that have been constructed by a Page limit of the MP-dS metrics [99]. On the
other hand, the new families of near-horizon geometries [156, 157], discussed in Section 4.5.3,
analytically continue to new examples of Einstein metrics on compact manifolds that have yet to be
explored.
give
the Einstein manifolds that have been constructed by a Page limit of the MP-dS metrics [99]. On the
other hand, the new families of near-horizon geometries [156, 157], discussed in Section 4.5.3,
analytically continue to new examples of Einstein metrics on compact manifolds that have yet to be
explored.
So far we have discussed analytic continuations in which the AdS2 is replaced by 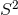 . Another
possibility is to replace the AdS2 with hyperbolic space
. Another
possibility is to replace the AdS2 with hyperbolic space 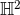 . For simplicity let us focus on static
near-horizon geometries. Such an analytic continuation is then easily achieved by replacing the global AdS2
time with imaginary time, i.e.,
. For simplicity let us focus on static
near-horizon geometries. Such an analytic continuation is then easily achieved by replacing the global AdS2
time with imaginary time, i.e., 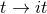 in Eq. (129
in Eq. (129 ). In this case, instead of a horizon, one gets a new
asymptotic region corresponding to
). In this case, instead of a horizon, one gets a new
asymptotic region corresponding to 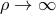 . General static Riemannian manifolds possessing an end that
is asymptotically extremal in this sense were introduced in [81
. General static Riemannian manifolds possessing an end that
is asymptotically extremal in this sense were introduced in [81 ]. Essentially, they are defined as static
manifolds possessing an end in which the metric can be written as an Euclideanised static spacetime
containing a smooth degenerate horizon. It was shown that Ricci flow preserves this class of manifolds,
and furthermore asymptotically-extremal Ricci solitons must be Einstein spaces [81
]. Essentially, they are defined as static
manifolds possessing an end in which the metric can be written as an Euclideanised static spacetime
containing a smooth degenerate horizon. It was shown that Ricci flow preserves this class of manifolds,
and furthermore asymptotically-extremal Ricci solitons must be Einstein spaces [81 ]. These
results were used to numerically simulate Ricci flow to find a new Einstein metric that has an
interesting interpretation in the AdS/CFT correspondence [81
]. These
results were used to numerically simulate Ricci flow to find a new Einstein metric that has an
interesting interpretation in the AdS/CFT correspondence [81 ], which we briefly discuss in
Section 7.5. It would be interesting to investigate non-static near-horizon geometries in this
context.
], which we briefly discuss in
Section 7.5. It would be interesting to investigate non-static near-horizon geometries in this
context.
7.5 Extremal branes
Due to the applications to black-hole solutions, we have mostly focused on the near-horizon geometries of
degenerate horizons with cross sections  that are compact. However, as we discussed in Section 2, the
concept of a near-horizon geometry exists for any spacetime containing a degenerate horizon, independent of
the topology of
that are compact. However, as we discussed in Section 2, the
concept of a near-horizon geometry exists for any spacetime containing a degenerate horizon, independent of
the topology of  . In particular, extremal black branes possess horizons with non-compact cross sections
. In particular, extremal black branes possess horizons with non-compact cross sections
 . Hence the general techniques discussed in this review may be used to investigate the classification of
the near-horizon geometries of extremal black branes. In general, this is a more difficult problem,
since as we have seen, compactness of
. Hence the general techniques discussed in this review may be used to investigate the classification of
the near-horizon geometries of extremal black branes. In general, this is a more difficult problem,
since as we have seen, compactness of 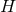 can often be used to avoid solving for the general
local metric by employing global arguments. Since it is outside the scope of this review, we
will not give a comprehensive overview of this topic; instead we shall select a few noteworthy
examples.
can often be used to avoid solving for the general
local metric by employing global arguments. Since it is outside the scope of this review, we
will not give a comprehensive overview of this topic; instead we shall select a few noteworthy
examples.
First consider AdSD space written in Poincaré coordinates
where . The surface
. The surface  , often called the Poincaré horizon, is a degenerate
Killing horizon of the Killing field
, often called the Poincaré horizon, is a degenerate
Killing horizon of the Killing field  . However, these coordinates are not valid at
. However, these coordinates are not valid at
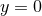 (the induced metric is singular) and hence are unsuitable for extracting the geometry of
the Poincaré horizon. One may introduce coordinates adapted to the Poincaré horizons by
constructing Gaussian null coordinates as described in Section 2. We need to find null geodesics
(the induced metric is singular) and hence are unsuitable for extracting the geometry of
the Poincaré horizon. One may introduce coordinates adapted to the Poincaré horizons by
constructing Gaussian null coordinates as described in Section 2. We need to find null geodesics
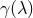 that in particular satisfy
that in particular satisfy 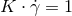 . Explicitly, this condition is simply
. Explicitly, this condition is simply  .
Now, since
.
Now, since 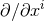 are Killing fields, along any geodesic the quantities
are Killing fields, along any geodesic the quantities 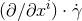 must be
constant; this gives
must be
constant; this gives 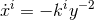 , where
, where 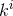 are constant along the geodesics. The null constraint
now simplifies to
are constant along the geodesics. The null constraint
now simplifies to 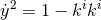 and so
and so 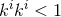 . This latter equation is easily integrated to
give
. This latter equation is easily integrated to
give 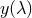 and using the above we may now integrate for
and using the above we may now integrate for 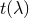 and
and 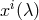 . The result is
where
. The result is
where  is an integration constant and we have set the other integration constants to zero to ensure the
horizon is at
is an integration constant and we have set the other integration constants to zero to ensure the
horizon is at 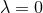 . This gives a family of null geodesics parameterised by
. This gives a family of null geodesics parameterised by 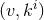 , which shoot out from
every point on the horizon; hence we may take the
, which shoot out from
every point on the horizon; hence we may take the 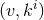 as coordinates on the horizon. We can then
change from Poincaré coordinates
as coordinates on the horizon. We can then
change from Poincaré coordinates 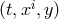 to the desired Gaussian null coordinates
to the desired Gaussian null coordinates 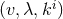 . Indeed,
one can check that in the coordinates
. Indeed,
one can check that in the coordinates 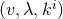 , the Killing field
, the Killing field 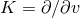 and the metric takes
the form (6
and the metric takes
the form (6 ) (with
) (with 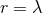 ). In fact, as is often the case, it is convenient to use a different
affine parameter
). In fact, as is often the case, it is convenient to use a different
affine parameter 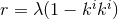 . Also, since
. Also, since 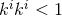 we may write
we may write 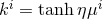 , where
, where
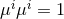 parameterise a unit
parameterise a unit 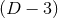 -sphere. Now the coordinate transformation becomes
and the AdSD metric in these coordinates is
It is now manifest that the surface
-sphere. Now the coordinate transformation becomes
and the AdSD metric in these coordinates is
It is now manifest that the surface 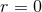 is a smooth degenerate Killing horizon of
is a smooth degenerate Killing horizon of 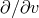 , corresponding
to the Poincaré horizon, which we may now extend onto and through by taking
, corresponding
to the Poincaré horizon, which we may now extend onto and through by taking 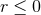 . Cross
sections of the Poincaré horizon are non-compact and of topology
. Cross
sections of the Poincaré horizon are non-compact and of topology 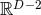 with a (non-flat)
induced metric given by the standard Einstein metric on hyperbolic space
with a (non-flat)
induced metric given by the standard Einstein metric on hyperbolic space 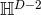 . Observe that
the above expresses AdSD as a warped product of AdS2 and hyperbolic space
. Observe that
the above expresses AdSD as a warped product of AdS2 and hyperbolic space 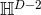 , i.e.,
as a static near-horizon geometry (with no need to take a near-horizon limit!), as observed
in [81
, i.e.,
as a static near-horizon geometry (with no need to take a near-horizon limit!), as observed
in [81 ].
].
The BPS extremal 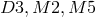 black branes of 10,11-dimensional supergravity are well known to have
a near-horizon geometry given by
black branes of 10,11-dimensional supergravity are well known to have
a near-horizon geometry given by 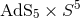 ,
, 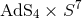 and
and 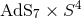 respectively with
their horizons corresponding to a Poincaré horizon in the AdS factor. However, as discussed
above, the standard Poincaré coordinates are not valid on the horizon and hence unsuitable
if one wants to extend the brane geometry onto and beyond the horizon. To this end, it is
straightforward to construct Gaussian null coordinates adapted to the horizon of these black
branes and check their near-horizon limit is indeed given by Eq. (140
respectively with
their horizons corresponding to a Poincaré horizon in the AdS factor. However, as discussed
above, the standard Poincaré coordinates are not valid on the horizon and hence unsuitable
if one wants to extend the brane geometry onto and beyond the horizon. To this end, it is
straightforward to construct Gaussian null coordinates adapted to the horizon of these black
branes and check their near-horizon limit is indeed given by Eq. (140 ) plus the appropriate
sphere.23
) plus the appropriate
sphere.23
Of course, extremal branes occur in other contexts. For example, the Randall–Sundrum model posits
that we live on a 3 + 1 dimensional brane in a 4 + 1-dimensional bulk spacetime with a negative
cosmological constant. A longstanding open problem has been to construct solutions to the
five-dimensional Einstein equations with a black hole localised on such a brane, the brane-world black
hole.24
In the five-dimensional spacetime, the horizons of such black holes extend out into the bulk. [147]
constructed the near-horizon geometry of an extremal charged black hole on a brane. This involved
constructing (numerically) the most general five dimensional static near-horizon geometry with 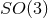 rotational symmetry, which turns out to be a 1-parameter family generalisation of Eq. (140
rotational symmetry, which turns out to be a 1-parameter family generalisation of Eq. (140 ) (this is the
5D analogue of the 4D general static near-horizon geometry with a non-compact horizon, see
Section 4.1).
) (this is the
5D analogue of the 4D general static near-horizon geometry with a non-compact horizon, see
Section 4.1).
Notably, [83] numerically constructed the first example of a brane-world black-hole solution. This corresponds to a Schwarzschild-like black hole on a brane suspended above the Poincaré horizon in AdS5. An important step towards this solution was the construction of a novel asymptotically AdS Einstein metric with a Schwarzschild conformal boundary metric and an extremal Poincaré horizon in the bulk (sometimes called a black droplet) [81]. This was found by numerically simulating Ricci flow on a suitable class of stationary and axisymmetric metrics. This solution is particularly interesting since by the AdS/CFT duality it is the gravity dual to a strongly coupled CFT in the Schwarzschild black hole, thus allowing one to investigate strongly coupled QFT in black-hole backgrounds. Recently, generalisations in which the boundary black hole is rotating have been constructed, in which case there is also the possibility of making the black hole on the boundary extremal [82, 84].

![[ ] ds2 = ℓ2Γ (y) − cosh2ρdt2 + dρ2 + γmn (y)dymdyn I 2 I J 2 J + γIJ(y)(dϕ + ℓ k sinh ρdt)(dϕ + ℓ k sinh ρdt ), (129 )](article1549x.gif)