1 Introduction
Equilibrium black-hole solutions to Einstein’s equations have been known since the advent of general relativity. The most obvious reason such solutions are of physical interest is the expectation that they arise as the end state of catastrophic gravitational collapse of some suitably localised matter distribution. A less obvious reason such solutions are important is that they have played a key role in guiding studies of quantum gravity.Classically equilibrium black holes are inert objects. However, the laws of black hole mechanics have a formal similarity with the laws of thermodynamics [17]. By studying quantum fields in a black-hole background, Hawking demonstrated that this is not a mere analogy and in fact quantum mechanically black holes are a thermodynamic system [128]. The black hole radiates at small temperature
proportional to the surface gravity of the horizon, and possesses a large entropy
proportional to the area
of the horizon, and possesses a large entropy
proportional to the area 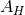 of spatial cross sections of the
horizon.1
of spatial cross sections of the
horizon.1
Deriving these semi-classical thermodynamic formulae from statistical mechanics requires a microscopic understanding of the “degrees of freedom” of the black hole. This has been a major motivation and driving force for quantum gravity research over the last four decades, although it is fair to say this is still poorly understood. It is in this context that extremal black holes are central. By definition, an equilibrium black hole is extremal (or extreme or degenerate), if the surface gravity
It immediately follows that the Hawking temperature vanishes – extremal black holes do not radiate after all! Hence, even semi-classically, extremal black holes are inert objects2 and as such are expected to have a simpler quantum description.The main purpose of this review is to discuss the classification of the near-horizon geometries of extremal black holes. There are a number of different motivations for considering this, which we will briefly review. As alluded to above, the principle reasons stem from studies in quantum gravity. In Section 1.1 and 1.2 we discuss the various ways extremal black holes and their near-horizon geometries have appeared in modern studies of quantum gravity. In Section 1.3 we discuss the more general black hole classification problem (which is also partly motivated by quantum gravity), and how near-horizon geometries provide a systematic tool for investigating certain aspects of this problem for extremal black holes.
1.1 Black holes in string theory
To date, the most promising candidate for a theory of quantum gravity is string theory. Famously, this
predicts the existence of extra spatial dimensions. As discussed above, an important test for any candidate
theory of quantum gravity is that it is able to explain the semi-classical formulae (1 ) and (2
) and (2 ). A major
breakthrough of Strominger and Vafa [200] was to use string theory to supply a microscopic derivation of
Eq. (2
). A major
breakthrough of Strominger and Vafa [200] was to use string theory to supply a microscopic derivation of
Eq. (2 ) for certain five dimensional extremal black holes.
) for certain five dimensional extremal black holes.
The black holes in question are higher-dimensional counterparts of the extremal Reissner–Nordström
(RN) black holes. These are supersymmetric solutions to a supergravity theory, which can be obtained as
a consistent Kaluza–Klein (KK) reduction of the ten/eleven dimensional supergravity that
describes string theory at low energies. Supersymmetry was crucial for their calculation, since
non-renormalisation results allowed them to perform a weak-coupling string calculation (involving
certain D-brane configurations) to deduce the entropy of the semi-classical black holes that
exist in the strong coupling regime (see [56] for a review). This was quickly generalised to
supersymmetric black holes with angular momentum [30 ] and supersymmetric four dimensional black
holes [171].
] and supersymmetric four dimensional black
holes [171].
An important assumption in these string theory calculations is that a given black hole is uniquely
specified by its conserved charges: its mass/energy, electric charge and angular momentum. For four
dimensional Einstein–Maxwell theory this follows from the black-hole uniqueness theorem (see [39 ] for a
review). However, Emparan and Reall demonstrated that black hole uniqueness is violated for
five-dimensional asymptotically-flat vacuum spacetimes [73
] for a
review). However, Emparan and Reall demonstrated that black hole uniqueness is violated for
five-dimensional asymptotically-flat vacuum spacetimes [73 ]. This was via the construction of an explicit
counterexample, the black ring, which is a black hole whose spatial horizon topology is
]. This was via the construction of an explicit
counterexample, the black ring, which is a black hole whose spatial horizon topology is 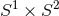 . Together
with the higher-dimensional analogues of the Kerr black hole (which have spherical topology) found
by Myers and Perry [183
. Together
with the higher-dimensional analogues of the Kerr black hole (which have spherical topology) found
by Myers and Perry [183 ], this established that the conserved charges are not sufficient to
specify a black hole uniquely and also that other horizon topologies are possible. Indeed, this
remarkable result motivated the study of stationary black holes in higher dimensional spacetimes.
Subsequently, a supersymmetric black ring was constructed [64
], this established that the conserved charges are not sufficient to
specify a black hole uniquely and also that other horizon topologies are possible. Indeed, this
remarkable result motivated the study of stationary black holes in higher dimensional spacetimes.
Subsequently, a supersymmetric black ring was constructed [64 , 66
, 66 ] that coexists with the
spherical topology black holes used in the original entropy calculations. Although microscopic
descriptions for the black rings have been proposed [20, 51], it is fair to say that the description of
black hole non-uniqueness within string theory is not properly understood (see [74] for a brief
review).
] that coexists with the
spherical topology black holes used in the original entropy calculations. Although microscopic
descriptions for the black rings have been proposed [20, 51], it is fair to say that the description of
black hole non-uniqueness within string theory is not properly understood (see [74] for a brief
review).
Any supersymmetric black hole is necessarily extremal. Since the Strominger–Vafa calculation, a substantial amount of work has been directed at removing the assumption of supersymmetry and extremality, with the ultimate goal being a string theory derivation of the thermodynamics of realistic black holes such as the four dimensional Schwarzschild or Kerr black holes. Although little progress has been made in the description of such non-extremal black holes, significant progress has been made for extremal non-supersymmetric black holes. In particular, this has been via the black-hole attractor mechanism.
The attractor mechanism is the phenomenon that the entropy of certain extremal black holes in string
theory does not depend on the moduli of the theory (typically scalar fields in the supergravity theory). This
was first observed for supersymmetric static black holes [78, 197, 77] although later it was realised it is
valid for generic extremal black holes [100, 194, 12]. The key idea is that extremal black holes have a
well-defined near-horizon geometry that typically possesses an AdS2 symmetry. Assuming this symmetry, it
was argued that the entropy must be independent of the moduli of the theory. Motivated by this, it was
then proved that the near-horizon geometry of any extremal black hole in this context must in fact possess
an AdS2 symmetry [162 ]. This general attractor mechanism thus ensures the black hole entropy is
independent of the string coupling, so it can be safely computed at weak coupling. This shows
that in fact it is extremality, rather than supersymmetry, that is behind the success of the
string theory microscopic calculations [52, 13]. This also explains the success of the entropy
calculations for extremal, non-supersymmetric black holes in four and five dimensions, e.g.,
[192, 71, 140].
]. This general attractor mechanism thus ensures the black hole entropy is
independent of the string coupling, so it can be safely computed at weak coupling. This shows
that in fact it is extremality, rather than supersymmetry, that is behind the success of the
string theory microscopic calculations [52, 13]. This also explains the success of the entropy
calculations for extremal, non-supersymmetric black holes in four and five dimensions, e.g.,
[192, 71, 140].
1.2 Gauge/gravity duality
A significant breakthrough in the study of quantum gravity is the Anti de Sitter/Conformal Field Theory
(AdS/CFT) duality [169 , 206, 207
, 206, 207 , 109]. In principle, AdS/CFT asserts a fully non-perturbative
equivalence of quantum gravity in asymptotically AdS spacetimes with a conformally invariant quantum
field theory in one lower spatial dimension. This is an explicit realisation of a ‘holographic principle’
underlying quantum gravity [202, 201].
, 109]. In principle, AdS/CFT asserts a fully non-perturbative
equivalence of quantum gravity in asymptotically AdS spacetimes with a conformally invariant quantum
field theory in one lower spatial dimension. This is an explicit realisation of a ‘holographic principle’
underlying quantum gravity [202, 201].
A crucial feature of the duality is that classical gravity in AdS spacetimes is dual to the strongly-coupled
regime in the CFT. This provides a precise framework to analyse the microscopic description of black holes
in terms of well-defined quantum field theories. The duality was originally proposed [169] in the context of
string theory on 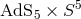 , in which case the CFT is the maximally supersymmetric four dimensional
, in which case the CFT is the maximally supersymmetric four dimensional
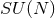 Yang–Mills gauge theory. However, the original idea has subsequently been generalised to a
number of dimensions and theories, and such gauge/gravity dualities are believed to hold more
generally.
Yang–Mills gauge theory. However, the original idea has subsequently been generalised to a
number of dimensions and theories, and such gauge/gravity dualities are believed to hold more
generally.
Classical non-extremal AdS black holes represent high-energy thermal states in the dual theory at large
 and strong coupling [207]. Strong coupling poses the main obstacle to providing a precise entropy
counting for such black holes, although excellent qualitative agreement can be found via extrapolating weak
coupling calculations [108, 23, 130
and strong coupling [207]. Strong coupling poses the main obstacle to providing a precise entropy
counting for such black holes, although excellent qualitative agreement can be found via extrapolating weak
coupling calculations [108, 23, 130 ]. Precise agreement has been achieved [198] for the asymptotically AdS3
Bañados–Teitelboim–Zanelli (BTZ) black hole (even for the non-extremal case) [15
]. Precise agreement has been achieved [198] for the asymptotically AdS3
Bañados–Teitelboim–Zanelli (BTZ) black hole (even for the non-extremal case) [15 ]. This is because
generically any theory of quantum gravity in AdS3 must be described by a two dimensional CFT2 with a
specific central charge [32]. This allows one to compute the entropy from Cardy’s formula, without
requiring an understanding of the microscopic degrees of freedom. In fact the string theory
calculations described in Section 1.1 can be thought of as applications of this method. This is
because the black holes in question can be viewed (from a higher-dimensional viewpoint) as
black strings with an AdS3 factor in the near-horizon geometry, allowing AdS3/CFT2 to be
applied.
]. This is because
generically any theory of quantum gravity in AdS3 must be described by a two dimensional CFT2 with a
specific central charge [32]. This allows one to compute the entropy from Cardy’s formula, without
requiring an understanding of the microscopic degrees of freedom. In fact the string theory
calculations described in Section 1.1 can be thought of as applications of this method. This is
because the black holes in question can be viewed (from a higher-dimensional viewpoint) as
black strings with an AdS3 factor in the near-horizon geometry, allowing AdS3/CFT2 to be
applied.
A major open problem is to successfully account for black-hole entropy using a higher dimensional
CFT. The best understood case is when the CFT is four dimensional, in which case the black
holes are asymptotically AdS5. As in the original string calculations, a strategy to overcome
the strong-coupling problem is to focus on supersymmetric AdS black holes. The dual CFT
states then belong to certain Bogomol’nyi–Prasad–Sommerfield (BPS) representations, and
so weak-coupling calculations may not receive quantum corrections. It turns out that such
black-hole solutions must rotate and hence are difficult to construct. In fact the first examples of
supersymmetric AdS5 black holes [120 , 119
, 119 ] were found via a classification of near-horizon geometries.
Subsequently, a more general four-parameter family of black-hole solutions were found [38
] were found via a classification of near-horizon geometries.
Subsequently, a more general four-parameter family of black-hole solutions were found [38 , 160
, 160 ]. The
problem of classifying all supersymmetric AdS black holes motivated further classifications of
near-horizon geometries, which have ruled out the possibility of other types of black hole such as
supersymmetric AdS black rings [154
]. The
problem of classifying all supersymmetric AdS black holes motivated further classifications of
near-horizon geometries, which have ruled out the possibility of other types of black hole such as
supersymmetric AdS black rings [154 , 161
, 161 , 106
, 106 ]. Despite significant effort, a microscopic derivation of the
entropy from the CFT has not yet been achieved in this context. Due to the low amount of
supersymmetry preserved by the black holes, it appears that non-zero coupling effects must be taken into
account [149, 22, 148, 21, 36].
]. Despite significant effort, a microscopic derivation of the
entropy from the CFT has not yet been achieved in this context. Due to the low amount of
supersymmetry preserved by the black holes, it appears that non-zero coupling effects must be taken into
account [149, 22, 148, 21, 36].
The original AdS/CFT duality was established by arguing that there exist two complementary
descriptions of the low energy physics of the string theory of a stack of 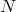 extremal D3 black branes. Near
the horizon of the D-brane only low energy excitations survive, which are thus described by string theory in
the
extremal D3 black branes. Near
the horizon of the D-brane only low energy excitations survive, which are thus described by string theory in
the 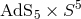 near-horizon geometry. On the other hand, the massless degrees of freedom
on a D-brane arrange themselves into (super)
near-horizon geometry. On the other hand, the massless degrees of freedom
on a D-brane arrange themselves into (super) 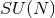 Yang–Mills theory. It is natural to
extend this idea to extremal black holes. Since extremal black holes typically possess an AdS2
factor in their near-horizon geometry, one may then hope that an AdS2/CFT1 duality [199]
could provide a microscopic description of such black holes. Unfortunately this duality is not
as well understood as the higher-dimensional cases. However, it appears that the black-hole
entropy can be reproduced from the degeneracy of the ground states of the dual conformal
mechanics [170
Yang–Mills theory. It is natural to
extend this idea to extremal black holes. Since extremal black holes typically possess an AdS2
factor in their near-horizon geometry, one may then hope that an AdS2/CFT1 duality [199]
could provide a microscopic description of such black holes. Unfortunately this duality is not
as well understood as the higher-dimensional cases. However, it appears that the black-hole
entropy can be reproduced from the degeneracy of the ground states of the dual conformal
mechanics [170 , 195].
, 195].
Another recently-developed approach is to generalise the AdS3/CFT2 derivation of the BTZ entropy to
describe more general black holes. This involves finding an asymptotic symmetry group of a given
near-horizon geometry that contains a Virasoro algebra and then applying Cardy’s formula. This was
applied to the extremal Kerr black hole and led to the Kerr/CFT correspondence [110], which is a proposal
that quantum gravity in the near-horizon geometry of extremal Kerr is described by a chiral CFT2
(see the reviews [31, 48]). This technique has provided a successful counting of the entropy of
many black holes. However, as in the AdS2/CFT1 case, the duality is poorly understood and it
appears that non-trivial excitations of the near-horizon geometry do not exist [60 , 4
, 4 ]. The
relation between these various approaches has been investigated in the special case of BTZ [16].
Furthermore, a CFT2 description has been proposed for a certain class of near-extremal black holes,
which possess a local near-horizon AdS3 factor but a vanishing horizon area in the extremal
limit [196, 146].3
]. The
relation between these various approaches has been investigated in the special case of BTZ [16].
Furthermore, a CFT2 description has been proposed for a certain class of near-extremal black holes,
which possess a local near-horizon AdS3 factor but a vanishing horizon area in the extremal
limit [196, 146].3
Recently, ideas from the gauge/gravity duality have been used to model certain phase transitions that occur in condensed-matter systems, such as superfluids or superconductors [107, 125]. The key motivation to this line of research, in contrast to the above, is to use knowledge of the gravitational system to learn about strongly-coupled field theories. Charged black holes in AdS describe the finite temperature phases. The non-superconducting phase is dual to the standard planar RN-AdS black hole of Einstein–Maxwell theory, which is stable at high enough temperature. However, at low enough temperatures this solution is unstable to the formation of a charged scalar condensate. The dominant phase at low temperatures is a charged black hole with scalar hair, which describes the superconducting phase. This instability of (near)-extremal RN-AdS can be understood as occurring due to the violation of the Breitenlohner–Freedmann bound in the AdS2 factor of the near-horizon geometry. A similar result has also been shown for neutral rotating AdS black holes [59]. The near-horizon AdS2 has also been used to provide holographic descriptions of quantum critical points and Fermi surfaces [76].
1.3 Black hole classification
The classification of higher-dimensional stationary black-hole solutions to Einstein’s equations is a major
open problem in higher dimensional general relativity (see [75 , 136] for reviews). As explained
above, the main physical motivation stems from studies of quantum gravity and high energy
physics. However, its study is also of intrinsic value both physically and mathematically. On the
physical side we gain insight into the behaviour of gravity in higher-dimensional spacetimes,
which in turn often provides renewed perspective for the classic four-dimensional results. On the
mathematical side, solutions to Einstein’s equation have also been of interest in differential
geometry [24].4
, 136] for reviews). As explained
above, the main physical motivation stems from studies of quantum gravity and high energy
physics. However, its study is also of intrinsic value both physically and mathematically. On the
physical side we gain insight into the behaviour of gravity in higher-dimensional spacetimes,
which in turn often provides renewed perspective for the classic four-dimensional results. On the
mathematical side, solutions to Einstein’s equation have also been of interest in differential
geometry [24].4
In four dimensions the black-hole uniqueness theorem provides an answer to the classification
problem for asymptotically-flat black-hole solutions of Einstein–Maxwell theory (see [39] for a
review).5
However, in higher dimensions, uniqueness is violated even for asymptotically-flat vacuum black holes. To
date, the explicit black-hole solutions known are the spherical horizon topology Myers–Perry black
holes [183 ] and the black rings [73, 187
] and the black rings [73, 187 ] that have
] that have 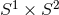 horizon topology (see [75] for a review). If
one allows for more complicated boundary conditions, such as KK asymptotics, then uniqueness is violated
even for static black holes (see, e.g., [141]). Although of less obvious physical relevance, the investigation of
asymptotically-flat vacuum black holes is the fundamental starting case to consider in higher dimensions,
since such solutions can be viewed as limits of black holes with more general asymptotics such as KK, AdS
and matter fields.
horizon topology (see [75] for a review). If
one allows for more complicated boundary conditions, such as KK asymptotics, then uniqueness is violated
even for static black holes (see, e.g., [141]). Although of less obvious physical relevance, the investigation of
asymptotically-flat vacuum black holes is the fundamental starting case to consider in higher dimensions,
since such solutions can be viewed as limits of black holes with more general asymptotics such as KK, AdS
and matter fields.
General results have been derived that constrain the topology of black holes. By generalising Hawking’s
horizon topology theorem [127 ] to higher dimensions, Galloway and Schoen [91
] to higher dimensions, Galloway and Schoen [91 ] have shown that the
spatial topology of the horizon must be such that it admits a positive scalar curvature metric (i.e., positive
Yamabe type). Horizon topologies are further constrained by topological censorship [85, 44
] have shown that the
spatial topology of the horizon must be such that it admits a positive scalar curvature metric (i.e., positive
Yamabe type). Horizon topologies are further constrained by topological censorship [85, 44 ]. For
asymptotically-flat (and globally AdS) black holes, this implies that there must be a simply connected
(oriented) cobordism between cross sections of the horizon and the
]. For
asymptotically-flat (and globally AdS) black holes, this implies that there must be a simply connected
(oriented) cobordism between cross sections of the horizon and the 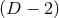 -dimensional sphere at spatial
infinity.6
In
-dimensional sphere at spatial
infinity.6
In 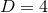 , this rules out toroidal black holes, although for
, this rules out toroidal black holes, although for 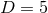 it imposes no constraint. For
it imposes no constraint. For
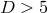 this does provide a logically independent constraint in addition to the positive Yamabe
condition [191
this does provide a logically independent constraint in addition to the positive Yamabe
condition [191 , 156
, 156 ].
].
General results have also been derived that constrain the symmetries of black hole
spacetimes. Firstly, asymptotically-flat, static vacuum black holes must be spherically
symmetric and hence are uniquely given by the higher dimensional Schwarzschild black
hole [98].7
By generalising Hawking’s rigidity theorem [127 ], it was shown that asymptotically-flat and
AdS stationary non-extremal rotating black holes must admit at least
], it was shown that asymptotically-flat and
AdS stationary non-extremal rotating black holes must admit at least 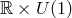 isometry
[137, 180
isometry
[137, 180 ] (for partial results pertaining to extremal rotating black holes see [134
] (for partial results pertaining to extremal rotating black holes see [134 ]). This additional
isometry can be used to further refine the allowed set of
]). This additional
isometry can be used to further refine the allowed set of 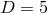 black hole horizon topologies
[133].
black hole horizon topologies
[133].
An important class of spacetimes, for which substantial progress towards classification has been made,
are the generalised Weyl solutions [72 , 124]. By definition these possess an
, 124]. By definition these possess an 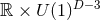 symmetry group
and generalise
symmetry group
and generalise 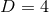 stationary and axisymmetric spacetimes. As in the
stationary and axisymmetric spacetimes. As in the 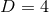 case, it turns out that
the vacuum Einstein equations for spacetimes with these symmetries are integrable. For
case, it turns out that
the vacuum Einstein equations for spacetimes with these symmetries are integrable. For 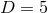 this
structure has allowed one to prove certain uniqueness theorems for asymptotically-flat black holes with
this
structure has allowed one to prove certain uniqueness theorems for asymptotically-flat black holes with
 symmetry, using the same methods as for
symmetry, using the same methods as for  [138
[138 ]. Furthermore, this has led to the
explicit construction of several novel asymptotically-flat, stationary, multi–black-hole vacuum solutions, the
first example being a (non-linear) superposition of a black ring and a spherical black hole [67].
For
]. Furthermore, this has led to the
explicit construction of several novel asymptotically-flat, stationary, multi–black-hole vacuum solutions, the
first example being a (non-linear) superposition of a black ring and a spherical black hole [67].
For 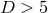 , the symmetry of these spacetimes is not compatible with asymptotic flatness,
that would require the number of commuting rotational symmetries to not exceed
, the symmetry of these spacetimes is not compatible with asymptotic flatness,
that would require the number of commuting rotational symmetries to not exceed 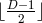 ,
the rank of the rotation group
,
the rank of the rotation group 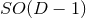 . In this case, Weyl solutions are compatible with
KK asymptotics and this has been used to prove uniqueness theorems for (uniform) KK black
holes/strings [139
. In this case, Weyl solutions are compatible with
KK asymptotics and this has been used to prove uniqueness theorems for (uniform) KK black
holes/strings [139 ].
].
The general topology and symmetry constraints discussed above become increasingly weak as one increases the number of dimensions. Furthermore, there is evidence that black hole uniqueness will be violated much more severely as one increases the dimensions. For example, by an analysis of gravitational perturbations of the Myers–Perry black hole, evidence for a large new family of black holes was found [193]. Furthermore, the investigation of “blackfolds”, where the long-range effective dynamics of certain types of black holes can be analysed, suggests that many new types of black holes should exist, see [70] for a review. In the absence of new ideas, it appears that the general classification problem for asymptotically-flat black holes is hopelessly out of reach.
As discussed in Section 1.2, the black-hole–classification problem for asymptotically AdS black holes is
of interest in the context of gauge/gravity dualities. The presence of a (negative) cosmological constant
renders the problem even more complicated. Even in four dimensions, there is no analogue of the
uniqueness theorems. One reason for this comes from the fact that Einstein’s equations with a
cosmological constant for stationary and axisymmetric metrics are not integrable. Hence the
standard method used to prove uniqueness of Kerr cannot be generalised. This also means that
constructing charged generalisations, in four and higher dimensions, from a neutral seed can not be
accomplished using standard solution generating methods. In fact, perturbation analyses of known
solutions (e.g., Kerr-AdS and higher dimensional generalisations), reveal that if the black holes
rotate sufficiently fast, super-radiant instabilities exist [130, 34, 159 , 35]. It has been suggested
that the endpoint of these instabilities are new types of non-axisymmetric black-hole solutions
that are not stationary in the usual sense, but instead invariant under a single Killing field
co-rotating with the horizon [159]. (Examples of such solutions have been constructed in a
scalar gravity theory [58]). A further complication in AdS comes from the choice of asymptotic
boundary conditions. In AdS there is the option of replacing the sphere on the conformal boundary
with more general manifolds, in which case topological censorship permits more black-hole
topologies [90
, 35]. It has been suggested
that the endpoint of these instabilities are new types of non-axisymmetric black-hole solutions
that are not stationary in the usual sense, but instead invariant under a single Killing field
co-rotating with the horizon [159]. (Examples of such solutions have been constructed in a
scalar gravity theory [58]). A further complication in AdS comes from the choice of asymptotic
boundary conditions. In AdS there is the option of replacing the sphere on the conformal boundary
with more general manifolds, in which case topological censorship permits more black-hole
topologies [90 ].
].
It is clear that supersymmetry provides a technically-simplifying assumption to classifying spacetimes,
since it reduces the problem to solving first-order Killing spinor equations rather than the full Einstein
equations. A great deal of work has been devoted to developing systematic techniques for constructing
supersymmetric solutions, most notably in five-dimensional ungauged supergravity [93 ] and gauged
supergravity [92]. These have been used to construct new five-dimensional supersymmetric black-hole
solutions, which are asymptotically flat [66
] and gauged
supergravity [92]. These have been used to construct new five-dimensional supersymmetric black-hole
solutions, which are asymptotically flat [66 , 64
, 64 ] and AdS [120
] and AdS [120 , 119, 160
, 119, 160 ], respectively. Furthermore, the
first uniqueness theorem for asymptotically-flat supersymmetric black holes was proved using these
methods [191
], respectively. Furthermore, the
first uniqueness theorem for asymptotically-flat supersymmetric black holes was proved using these
methods [191 ].
].
Less obviously, it turns out that the weaker assumption of extremality can also be used as a simplifying
assumption, as follows. The event horizon of all known extremal black holes is a degenerate Killing horizon
with compact spatial cross sections 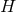 . It turns out that restricting Einstein’s equations for
a
. It turns out that restricting Einstein’s equations for
a 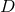 -dimensional spacetime to a degenerate horizon gives a set of geometric equations for
the induced metric on such
-dimensional spacetime to a degenerate horizon gives a set of geometric equations for
the induced metric on such 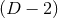 -dimensional cross sections
-dimensional cross sections 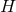 , that depend only on
quantities intrinsic to
, that depend only on
quantities intrinsic to 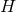 . By studying solutions to this problem of Riemannian geometry on a
compact manifold
. By studying solutions to this problem of Riemannian geometry on a
compact manifold 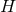 , one can thus consider the possible horizon geometries (and topologies)
independently of the full parent spacetime. This strategy often also works in cases where the
standard black hole uniqueness/classification techniques do not apply (e.g., AdS, higher dimensions
etc.).
, one can thus consider the possible horizon geometries (and topologies)
independently of the full parent spacetime. This strategy often also works in cases where the
standard black hole uniqueness/classification techniques do not apply (e.g., AdS, higher dimensions
etc.).
One can understand this feature of degenerate horizons in terms of the near-horizon limit, which, as we
explain in Section 2, exists for any spacetime containing a degenerate horizon. This allows one to define an
associated near-horizon geometry, which must also satisfy the full Einstein equations [191 , 162
, 162 ], so
classifying near-horizon geometries is then equivalent to classifying possible horizon geometries (and
topologies). Indeed, the topic of this review is the classification of near-horizon geometries in diverse
dimensions and theories.
], so
classifying near-horizon geometries is then equivalent to classifying possible horizon geometries (and
topologies). Indeed, the topic of this review is the classification of near-horizon geometries in diverse
dimensions and theories.
The classification of near-horizon geometries allows one to explore in a simplified setup the main issues that
appear in the general black-hole classification problem, such as the horizon topology, spacetime symmetry
and the “number” of solutions. The main drawback of this approach is that the existence of a near-horizon
geometry solution does not guarantee the existence of a corresponding black-hole solution (let alone its
uniqueness).8
Hence, one must keep this in mind when interpreting near-horizon classifications in the context of black
holes, although definite statements can be learned. In particular, one can use this method to rule out
possible black-hole horizon topologies, for if one can classify near-horizon geometries completely and a
certain horizon topology does not appear, this implies there can be no extremal black hole with that horizon
topology either. A notable example of this method has been a proof of the non-existence of supersymmetric
AdS black rings in 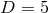 minimal gauged supergravity [161
minimal gauged supergravity [161 , 106
, 106 ].
].
1.4 This review
1.4.1 Scope
In this review we will consider near-horizon geometries of solutions to Einstein’s equations, in all dimensions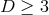 , that contain smooth degenerate horizons. Our aim is to
provide a unified treatment of such near-horizon solutions in diverse theories with matter content
ranging from vacuum gravity, to Einstein–Maxwell theories and various (minimal) supergravity
theories.
, that contain smooth degenerate horizons. Our aim is to
provide a unified treatment of such near-horizon solutions in diverse theories with matter content
ranging from vacuum gravity, to Einstein–Maxwell theories and various (minimal) supergravity
theories.
We do not assume the near-horizon geometry arises as a near-horizon limit of a black-hole solution. However, due to the application to extremal black holes we will mostly consider horizons that admit a spatial cross section that is compact. As we will see in various setups, compactness often allows one to avoid explicitly solving the full Einstein equations and instead use global arguments to constrain the space of solutions. As a result, the classification of near-horizon geometries with non-compact horizon cross sections is a much more difficult problem about which less is known. This is relevant to the classification of extremal black branes and therefore lies outside the scope of this article. Nevertheless, along the way, we will point out cases in which classification has been achieved without the assumption of compactness, and in Section 7.5 we briefly discuss extremal branes in this context.
Although this is a review article, we streamline some of the known proofs and we also present several new results that fill in various gaps in the literature. Most notably, we fully classify three dimensional near-horizon geometries in vacuum gravity and Einstein–Maxwell–Chern–Simons theories, in Section 4.2 and 6.1 respectively, and classify homogeneous near-horizon geometries in five dimensional Einstein–Maxwell–Chern–Simons theories in Section 6.3.2.
1.4.2 Organisation
In Section 2 we provide key definitions, introduce a suitably general notion of a near-horizon geometry and set up the Einstein equations for such near-horizon geometries.
In Section 3 we review various general results that constrain the topology and symmetry of near-horizon geometries. This includes the horizon topology theorem and various near-horizon symmetry enhancement theorems. We also discuss the physical charges one can calculate from a near-horizon geometry.
In Section 4 we discuss the classification of near-horizon geometries in vacuum gravity, including a cosmological constant, organised by dimension. In cases where classification results are not known, we describe the known solutions.
In Section 5 we discuss the classification of supersymmetric near-horizon geometries in various supergravity theories, organised by dimension.
In Section 6 we discuss the classification of general near-horizon geometries coupled to gauge fields. This
includes 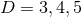 Einstein–Maxwell theories, allowing for Chern–Simons terms where appropriate, and
Einstein–Maxwell theories, allowing for Chern–Simons terms where appropriate, and
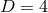 Einstein–Yang–Mills theory.
Einstein–Yang–Mills theory.
In Section 7 we discuss various applications of near-horizon geometries and related topics. This includes uniqueness/classification theorems of the corresponding extremal black-hole solutions, stability of near-horizon geometries and extremal black holes, geometric inequalities, analytic continuation of near-horizon geometries, and extremal branes and their near-horizon geometries.