List of Footnotes
| 1 | An interesting, unanswered question is if there are any missing populations of black holes, e.g., “intermediate” mass black
holes in the range 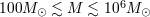 [180, 203, 90 [180, 203, 90 , 67 , 67 ] or “primordial” black holes [56]. ] or “primordial” black holes [56]. |
|
| 2 | ![M ⊙ = 1.99 × 1033 [g]](article1x.gif) denotes the mass of the Sun, used in astrophysics as a mass unit. denotes the mass of the Sun, used in astrophysics as a mass unit. |
|
| 3 | Radiant power in astrophysics is traditionally called “luminosity.” At the Eddington luminosity,
![LEdd ≡ 1.2× 1038M ∕M⊙ [erg∕s]](article4x.gif) , radiation force balances the gravity of the central object (with mass , radiation force balances the gravity of the central object (with mass 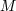 ). In the
case of stars, “super-Eddington” luminosities, ). In the
case of stars, “super-Eddington” luminosities, 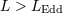 , are not possible, as this would mean radiation pressure
would blow the star apart. , are not possible, as this would mean radiation pressure
would blow the star apart. |
|
| 4 | Observations of black holes may eventually cast light on the quantum gravity structure of the physical vacuum [3 ],
possibly constraining string theory [64] and the hypothesis of extra dimensions [21, 251, 140]. ],
possibly constraining string theory [64] and the hypothesis of extra dimensions [21, 251, 140]. |
|
| 5 | Strictly speaking, this statement is only true for nearly spherical gravity sources. Higher order (octopole) moments allow for the formation of an ISCO, even in Newtonian theory [15]. | |
| 6 | Astrophysical black holes do not themselves radiate. The temperature associated with Hawking radiation is
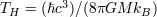 . For a stellar-mass black hole . For a stellar-mass black hole ![TH ∼ 10−8[∘ K ]](article22x.gif) . Thus, Hawking radiation is completely suppressed
by the thermal bath of the . Thus, Hawking radiation is completely suppressed
by the thermal bath of the ![3[∘ K]](article23x.gif) cosmic background radiation. For supermassive black holes, the Hawking temperature is at
least five orders of magnitude smaller still. cosmic background radiation. For supermassive black holes, the Hawking temperature is at
least five orders of magnitude smaller still. |
|
| 7 | The rate 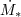 at which matter accretes is therefore regulated by internal torques and radiative processes. Only if at which matter accretes is therefore regulated by internal torques and radiative processes. Only if
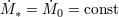 everywhere, with everywhere, with 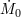 being the outside mass supply, can the accretion process be stationary. Since the
internally determined being the outside mass supply, can the accretion process be stationary. Since the
internally determined 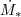 may change due to instabilities, limit cycles, etc., an occurrence of a really long-term steady
accretion flow should be considered a fine-tuned eigenstate. Note, too, that in many astrophysical situations may change due to instabilities, limit cycles, etc., an occurrence of a really long-term steady
accretion flow should be considered a fine-tuned eigenstate. Note, too, that in many astrophysical situations 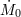 is also
genuinely variable. is also
genuinely variable. |
|
| 8 | This makes black hole accretion the most efficient energy generation process in the universe, short of matter-antimatter annihilation. | |
| 9 | Note that there is an analogy with stars, where there are three timescales – dynamical, thermal, and nuclear – which for
most of the life of a star obey 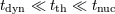 . . |
|
| 10 | The slow rotation cases are sometimes referred to as “Bondi flows” in honor of Bondi’s pioneering works on spherically-symmetric (non-rotating) accretion [50]. | |
| 11 | “Well, in our country,“ said Alice, still panting a little, “you’d generally get to somewhere else if you run very fast for a long time, as we’ve been doing.” “A slow sort of country!” said the Queen. “Now, here, you see, it takes all the running you can do, to keep in the same place.” | |
| 12 | For a congruence of observers (or particles or photons) with four velocity 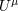 , the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment , the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment 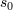 , occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment , occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment 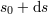 . The volume change . The volume change 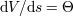 is called
expansion. The shear tensor is called
expansion. The shear tensor 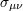 measures the ellipsoidal distortion of this sphere, and the vorticity tensor measures the ellipsoidal distortion of this sphere, and the vorticity tensor 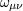 describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor 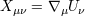 in the following way: in the following way: 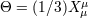 , , 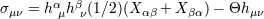 , and , and
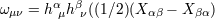 . Here . Here 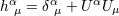 is the projection tensor. The acceleration is the projection tensor. The acceleration 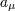 is also considered
a kinematic invariant. is also considered
a kinematic invariant. |
|
| 13 | For the benefit of readers who are unfamiliar with the phenomenology of relativistic jets we mention that many jets demonstrate incredibly consistent collimation, even along hundreds or thousands of kiloparsecs (e.g. [114]). From this we can infer that such jets have maintained their orientation and outflow for millions of years. | |
| 14 | Radio loud AGN are 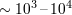 times brighter in radio than radio quiet AGN of comparable optical
luminosities [289]. times brighter in radio than radio quiet AGN of comparable optical
luminosities [289]. |
|
| 15 | It is quite remarkable that the mathematical theory describing resonances makes some very general predictions about the behavior of frequencies and amplitudes, even if the specific physical properties of the oscillating objects are not known. To some extent it is possible to accurately describe how things oscillate without even knowing what is oscillating. | |
| 16 | The mathematical foundations of the resonance model are described and discussed in a special issue of the Astronomische Nachrichten [2]. |

