1 Introduction
Because of its firm connection to black holes themselves, black hole accretion disk theory belongs to the realm of fundamental physics. However, the theory itself employs a complicated maze of fluid-dynamics results and several phenomenological estimates and guesses known only to specialists. This Living Review aims to give readers a useful guide, a “road map” if you will, through the unavoidable complexity of the subject.Below we list fourteen “Destinations” on this road map and explain their logical connections. In our opinion, these Destinations are the key issues, or landmarks, of the theory being reviewed. The particular road map that we present is, of course, biased by our own ideas and research histories. However, we are confident that the grand landscape of this field will, nevertheless, shine through in the end.
We start by pointing out that black holes are one of the most remarkable inventions of the human mind. Their bizarre properties capture nearly everyone’s imagination, from Princeton string theorists to Hollywood movie makers. Initially, black holes only existed virtually, as weird theoretical and mathematical ideas. Models of them were studied with interest, but their real existence was questioned by many, including Albert Einstein himself. This situation changed in the latter part of the twentieth century, after unambiguous and robust detections were made of several astrophysical black hole “candidates” within our Galaxy and in many others. Thus far, two1 classes of black holes have been observed by astronomers. In our theory-minded Living Review we do not give detailed descriptions of their observational properties. Instead, we stress their importance by starting our road map from the two classes of observed black holes:
- Destination 1:
-
Quasars and other similar supermassive objects, which are collectively called “active galactic nuclei” (or AGN), having masses2 in the range
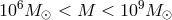 . They reside at centers of our and other galaxies. The
“active” ones among them are the most powerful steady energy sources known in the universe.
Many have radiant powers
. They reside at centers of our and other galaxies. The
“active” ones among them are the most powerful steady energy sources known in the universe.
Many have radiant powers 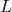 in excess of their corresponding Eddington luminosities.3
The high efficiency of quasars,
in excess of their corresponding Eddington luminosities.3
The high efficiency of quasars, 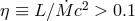 , where
, where 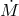 is the mass supply rate from
accretion (“the accretion rate”), is puzzling. Black hole accretion disk theory predicts that
is the mass supply rate from
accretion (“the accretion rate”), is puzzling. Black hole accretion disk theory predicts that
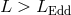 would imply small accretion efficiency
would imply small accretion efficiency 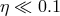 . However, the famous “Sołtan
argument,” based on quasar counts, shows that on a long time average,
. However, the famous “Sołtan
argument,” based on quasar counts, shows that on a long time average, 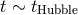 , quasars
can have both
, quasars
can have both 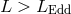 and
and 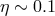 [290, 254]. AGN are described in much greater detail
in the authoritative monograph by Krolik [163].
[290, 254]. AGN are described in much greater detail
in the authoritative monograph by Krolik [163].
- Destination 2:
-
Microquasars and similar “stellar-mass” black holes, having
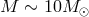 . The term
“microquasars” was invented by Mirabel [206] to convey that these objects, in many regards,
behave like scaled-down versions of quasars. A few tens of them have been found in our Galaxy
as members of X-ray binaries [184
. The term
“microquasars” was invented by Mirabel [206] to convey that these objects, in many regards,
behave like scaled-down versions of quasars. A few tens of them have been found in our Galaxy
as members of X-ray binaries [184 ]. The natural scaling (time)
]. The natural scaling (time) 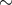 (mass) adds importance
to observations of microquasar variability, because the same processes that takes hundreds of
years (say) in quasars, takes only minutes in microquasars. Particularly interesting are spectral
state changes, which occur on timescales
(mass) adds importance
to observations of microquasar variability, because the same processes that takes hundreds of
years (say) in quasars, takes only minutes in microquasars. Particularly interesting are spectral
state changes, which occur on timescales 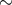 1 day (see [258
1 day (see [258 ] for a review), and quasi-periodic
oscillations (QPOs), which have timescales as short as
] for a review), and quasi-periodic
oscillations (QPOs), which have timescales as short as 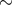 1 ms [308, 184
1 ms [308, 184 , 258
, 258 ].
].
Quasars and microquasars are among the most intriguing astrophysical objects ever discovered, and the goal of black hole accretion disk theory is, obviously, to explain their observed properties – but one hopes for much more! One hopes that observations of quasars and microquasars, together with their proper theoretical interpretation, would eventually test the very heart of black hole physics itself. When this happens, we may meaningfully constrain our knowledge of the fundamental properties of space and time.4
To accomplish this goal, black hole accretion disk theory must find ways to filter out from the observational data the parts that bear clear black hole signatures from the remaining dirty astrophysics parts. The logical structure of our Living Review attempts to reflect as closely as possible this main task of the theory. Thus, our review starts (in Section 2) with the pure gravity part, concentrating on the three particular signatures of black hole gravity that are crucial to black hole accretion disk theory:
- Destination 3:
-
Event horizon. This is a sphere of radius
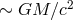 surrounding the black hole singularity,
from within which nothing may emerge – a one-way membrane. Note that this means that
black holes have no rigid surfaces. This is a unique signature of black holes; other relativistic
features may be observable around non-black hole objects, specifically sufficiently compact
neutron stars, but the event horizon is a defining property of black holes.
surrounding the black hole singularity,
from within which nothing may emerge – a one-way membrane. Note that this means that
black holes have no rigid surfaces. This is a unique signature of black holes; other relativistic
features may be observable around non-black hole objects, specifically sufficiently compact
neutron stars, but the event horizon is a defining property of black holes.
- Destination 4:
-
Ergosphere. This is a region around a rotating black hole where spacetime itself is dragged along in the direction of rotation at a speed greater than the local speed of light in relation to the rest of the universe. In this region, negative energy states are possible, which means that the rotational energy of the black hole can be tapped through various manifestations of the “Penrose process” [242
 ].
].
- Destination 5:
-
Marginally stable orbit (also called the “innermost stable circular orbit” or ISCO). This is the smallest circle (
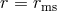 ) along which free particles may stably orbit around a black hole.
No stable circular motion is possible for
) along which free particles may stably orbit around a black hole.
No stable circular motion is possible for 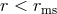 . This is a unique feature of relativity, as in
Newtonian theory, orbits at all radii are possible.5
. This is a unique feature of relativity, as in
Newtonian theory, orbits at all radii are possible.5
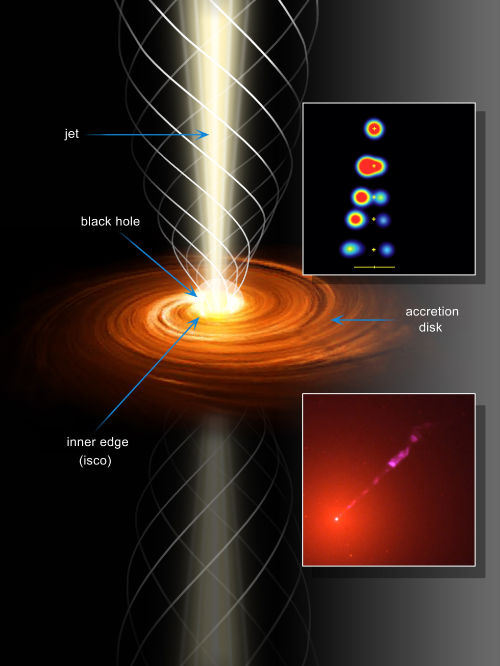
As fascinating as these destinations are, they are not easily probed in nature.
The radiation we receive from quasars and microquasars comes not from the black
holes themselves, but instead originates in the accretion disks which surround
them6
(see Figure 1 ). In these accretion disks, angular momentum is gradually removed by some presumably
(although not necessarily [48
). In these accretion disks, angular momentum is gradually removed by some presumably
(although not necessarily [48 ]) dissipative process, causing matter to spiral down into the black hole,
converting its gravitational energy into heat, and then, by various processes, radiating this
energy.7
The radiation subsequently leaks through the disk, escapes from its surface, and travels along trajectories
curved (in space) by the strong gravity of the black hole, eventually reaching our telescopes. Bingo! That is
what we are interested in this Living Review.
]) dissipative process, causing matter to spiral down into the black hole,
converting its gravitational energy into heat, and then, by various processes, radiating this
energy.7
The radiation subsequently leaks through the disk, escapes from its surface, and travels along trajectories
curved (in space) by the strong gravity of the black hole, eventually reaching our telescopes. Bingo! That is
what we are interested in this Living Review.
The preceding description of how black hole accretion works is well established in general, yet several rather crucial details remain either not sufficiently understood or are too complex to be studied even by the most powerful present-day computers. To deal with this seemingly hopeless situation, several purely phenomenological approaches have been adopted. Two of them should certainly be marked as Destinations, in and of themselves, on the road map, because they are among the very basic ingredients of the accretion process:
- Destination 6:
-
Angular momentum transport and energy dissipation. The quasi-steady accretion of a particle of mass
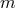 through a Keplerian disk from a large outer radius,
through a Keplerian disk from a large outer radius, 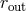 , to an inner radius,
, to an inner radius, 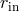 ,
requires that the particle give up an amount of energy8
,
requires that the particle give up an amount of energy8
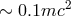 . To do this, the particle must also give up an amount of angular momentum
. To do this, the particle must also give up an amount of angular momentum
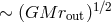 . We will see in Section 3.2 that viscous stresses within the fluid can facilitate
this (mass transfer in, angular momentum transfer out, and energy dissipation). However,
the stresses can not come from ordinary molecular viscosity, as this is much too weak in
astrophysical accretion disks. Instead, the stresses likely come from turbulence that acts like
an effective viscosity.
. We will see in Section 3.2 that viscous stresses within the fluid can facilitate
this (mass transfer in, angular momentum transfer out, and energy dissipation). However,
the stresses can not come from ordinary molecular viscosity, as this is much too weak in
astrophysical accretion disks. Instead, the stresses likely come from turbulence that acts like
an effective viscosity.
- Destination 7:
-
Radiative processes and radiative transfer. These depend on the thermodynamic state of matter (electron density, ion density, temperature), its motion, and the magnetic field, but most importantly on whether the matter is opaque or transparent to radiation, i.e., whether its optical depth is large,
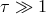 , or small,
, or small, 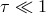 . In the general case when the matter is
optically thick
. In the general case when the matter is
optically thick 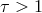 , the accretion disk can be quite luminous and also efficiently cooled by
radiation. Accretion disks with
, the accretion disk can be quite luminous and also efficiently cooled by
radiation. Accretion disks with 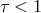 are inefficiently cooled and thus less luminous.
are inefficiently cooled and thus less luminous.
With these complexities, it is useful to have both analytic theories and numerical simulations to
facilitate progress in the field. Before getting into details, though, let us simply study the parameter space
available before us. Let us first consider three generic types of physical processes that must occur in black
hole accretion disks: “dynamical” processes with a characteristic time-scale, 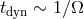 , where
, where 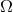 is the
orbital angular velocity; “thermal” processes with a characteristic time-scale,
is the
orbital angular velocity; “thermal” processes with a characteristic time-scale, 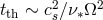 , where
, where 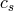 is
the sound speed and
is
the sound speed and 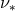 is the kinematic viscosity; and “viscous” processes with a characteristic
time-scale,
is the kinematic viscosity; and “viscous” processes with a characteristic
time-scale, 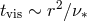 , where
, where  is the radial distance from the black hole. One excepts that,
typically,9
is the radial distance from the black hole. One excepts that,
typically,9
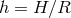 ; dimensionless accretion rate,
; dimensionless accretion rate,
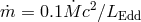 ; optical depth,
; optical depth, 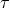 ; importance of advection,
; importance of advection, 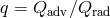 , where
, where 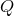 represents
an energy flux; importance of radiation pressure,
represents
an energy flux; importance of radiation pressure, 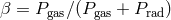 ; location of inner edge,
; location of inner edge, 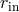 ; and
accretion efficiency
; and
accretion efficiency 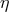 .
.
| Fast rotation (Disk) | Slow rotation (Bondi) | |
| Large pressure | slim, thick | ADAFs |
| Small pressure | thin | free-fall |
| Accretion rate high | Accretion rate low | |
| Large opacity | slim, thick | thin |
| Small opacity | – | ADAF |
- Destination 8:
-
Thick Disk.
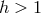 ,
, 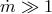 ,
, 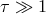 ,
, 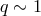 ,
, 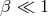 ,
, 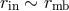 ,
, 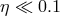
- Destination 9:
-
Thin Disk.
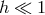 ,
, 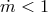 ,
, 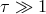 ,
, 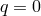 ,
, 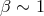 ,
, 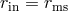 ,
, 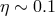
- Destination 10:
-
Slim Disk.
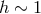 ,
, 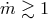 ,
, 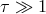 ,
, 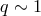 ,
, 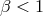 ,
, 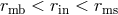 ,
, 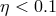
- Destination 11:
-
Advection-Dominated Accretion Flow (ADAF).
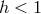 ,
, 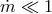 ,
, 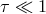 ,
, 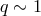 ,
, 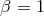 ,
, 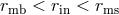 ,
, 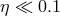
Interestingly, the parameter space of each of these types of accretion disks overlaps that of other solutions. For instance, ADAF solutions exist that have the same mass accretion rates as thin disk solutions [59]. In such cases, it is not clear how nature might choose one over the other.
In Sections 4 – 7, we will demonstrate that analytic (or at least semi-analytic) models exist for each of these types of accretion disks. However, this does not guarantee that they are stable. The issue of stability is our next destination.
- Destination 12:
-
Stability. Stability analysis is important because the systematic differential rotation that is one of the defining characteristics of accretion disks is also a potential source of destabilizing energy. On the one hand, this may be essential, as the angular momentum transport and energy dissipation required for accretion may require disks to be mildly unstable. On the other hand, if a model is violently unstable, then the basic assumption of a “steady-state” would be violated.
Along with stability, we also look at the natural oscillation modes associated with accretion disks. The frequencies of some of these modes are tied to the properties of the black hole space-time, which is how these relate to the fundamental physics issues of interest in this Living Review.
- Destination 13:
-
Oscillations. As with any finite distribution of fluid, accretion disks have natural oscillation modes associated with them. If these modes can be excited at appreciable amplitudes, they may be able to modify the observed light curve of the disk in measurable ways. This makes disk oscillations a leading candidate for explaining the quasi-periodic oscillations (QPOs) that we discuss in Section 12.4.
Because of the close observational links between black hole accretion disks and jets [92 , 94
, 94 ], we include jets as
the final Destination of our review.
], we include jets as
the final Destination of our review.
- Destination 14:
-
Jets. Jets are narrow (
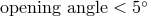 ), long (
), long (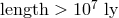 in the case of AGN), and
fast (
in the case of AGN), and
fast (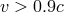 ) streams of matter emerging from very compact regions around the black hole,
usually in opposite directions, presumably normal to the plane of the accretion disk. Jets can
play a significant role in transporting energy and angular momentum away from the accretion
disk [48
) streams of matter emerging from very compact regions around the black hole,
usually in opposite directions, presumably normal to the plane of the accretion disk. Jets can
play a significant role in transporting energy and angular momentum away from the accretion
disk [48 ]. They also play an important role in shaping the black hole’s environment far beyond
the gravitational reach of the black hole itself, affecting galactic evolution, particle acceleration,
and intragalactic ionization.
]. They also play an important role in shaping the black hole’s environment far beyond
the gravitational reach of the black hole itself, affecting galactic evolution, particle acceleration,
and intragalactic ionization.
Going hand-in-glove with analytic models of accretion disks are direct numerical simulations. Although analytic theories have been extremely successful at explaining many general observational properties of quasars and microquasars, numerical simulations can be critically important in at least two respects: 1) as an extension of analytic work, by treating nonlinear perturbations and higher order coupling terms, and 2) in cases that are highly time variable or contain little symmetry, such that the prospects of finding an analytic solution are poor. There is also an important overlap region where various analytic and numerical methods are applicable and can be used to independently validate results. Because of these close connections between analytic and numerical work, we have dedicated Section 11 to the discussion and review of direct numerical simulation of black hole accretion disks.
We finish this Living Review with Section 12, which tries to make some connections between the concepts discussed in earlier sections and actual observational phenomena. We emphasize that we are not aiming to provide a comprehensive review of black hole observations, but rather to highlight a very small subset of these that are of particular relevance to our review.
Throughout this review, we adopt the  metric signature and often use units where
metric signature and often use units where
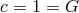 . To make all physical quantities dimensionless, we sometimes also use the mass of the
black hole as a unit,
. To make all physical quantities dimensionless, we sometimes also use the mass of the
black hole as a unit, 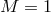 . We use the common Einstein summation convention, where
repeated indices in a formula imply summation over the range of that index. We also follow the
common convention where Greek (Latin) indices are used for four-(three-)dimensional tensor
quantities.
. We use the common Einstein summation convention, where
repeated indices in a formula imply summation over the range of that index. We also follow the
common convention where Greek (Latin) indices are used for four-(three-)dimensional tensor
quantities.