10 Relativistic Jets

Although the main focus of this review is on black hole accretion disk theory, we note that there has long been a strong observational connection between accreting black holes and relativistic jets across all scales of black hole mass. For supermassive black holes this includes quasars and active galactic nuclei; for stellar-mass black holes this includes microquasars. However, the theoretical understanding of disks and jets has largely proceeded separately and the physical link between the two still remains uncertain. Therefore, we present only a few brief comments on the subject in this review. More complete discussions of the theory of relativistic jets may be found in [193]. A review of their observational connection to black holes is given in [205].

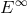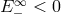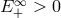In Section 2.2, we described the “Penrose process,” whereby rotational energy may be extracted from a black hole and carried to an observer at infinity. To briefly recap, Penrose [242, 243] imagined a freely falling particle with energy disintegrating into two particles with energies and . Then, the particle with negative energy 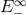falls into the black hole, and the other one escapes to infinity. Clearly, 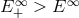, so that there is a net gain of energy.

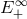It was first suggested by Wheeler at a 1970 Vatican conference and soon after by others [183, 96] that such a Penrose process may explain the energetics of superluminal jets commonly seen emerging from quasars and other black hole sources. However, a number of authors [31, 314, 161] showed that for to be greater than 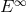, the disintegration process must convert most of the rest mass energy of the infalling particle to kinetic energy, in the sense that, in the center-of-mass frame, the particle must have velocity 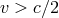. The argument of Wald [314] is powerful, short and elegant, so we give it here in extenso.

Let 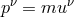be the four momentum of a particle with the mass . We assume that in the ZAMO frame (Section 2.2) the particle has a four velocity of the form, 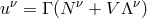, where 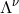is a timelike-unit vector (for simplicity we assume ), 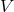is the particle 3-velocity in the ZAMO frame, and 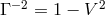. If the disintegration fragments move in the directions 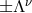(which one may prove is energetically most favorable), then the four velocities of these fragments in the center-of-mass frame are,

The form of (118) follows from the Lorentz transformation 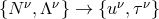. Multiplying (117) by gives Since 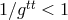and realistic particles have 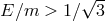, the condition 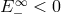necessarily requires . Such highly relativistic disintegration events are not generally seen in nature. To make matters worse, from the upper limit of (119), Wald deduced that the presence of the black hole limits the energy increase to a maximal factor of 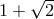. Thus, he concluded [314]: “The Penrose mechanism cannot serve as a useful energy source for astrophysical processes. In no case can one obtain energies which are greater by a significant factor than those which already could be obtained by a similar breakup process without the presence of the black hole.”

Replacing particle disintegration with particle collision does not help, even though the center-of-mass energy of such a collision happening arbitrarily close to the horizon of the maximally rotating Kerr black hole may be arbitrarily large [247, 28]. This is because the Wald limit of 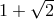still holds [39]. It would seem that even under idealized conditions, the maximal energy of a particle escaping via the Penrose process is only a modest factor above the total initial energy [39].

Therefore, we consider a general matter distribution, described by an unspecified stress-energy tensor 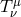. In this case, the energy flux in the ZAMO frame is 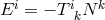, and the energy absorbed by the black hole is

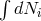where is the surface integral over the horizon. The inequality sign follows from the fact that the locally measured energy must be positive. The above integral may by transformed into As in the classic Penrose process, the necessary condition for the energy gain is: Thus, in a way fully analogous to the Penrose process for particles (18), one may say that if the energy at infinity increases because the black hole absorbed negative-at-infinity energy, then the black hole rotation must also slow down by absorbing matter with negative angular momentum.

Blandford and Znajek [49] made the brilliant discovery that an electromagnetic form of the Penrose process may work. In their model, the energy for the jet is extracted from the spin energy of the black hole via a torque provided by magnetic field lines that thread the event horizon or ergosphere. The estimated luminosity of the jet is given by [178] (although see [303] for higher order expressions that apply when )

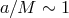where is a measure of the effect of the angular velocity of the field 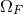relative to that of the hole 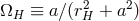, 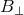is the magnetic field normal to the horizon, and 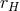is the radius of the event horizon (14). In this model, the only purpose of the disk is to act as the current sheet which continually provides magnetic field to the black hole. This last point led to one of the main objections to the Blandford–Znajek model: Ghosh and Abramowicz [109] argued on astrophysical grounds that accretion disks simply cannot feed the required fields into the black hole. However, recent work by Rothstein and Lovelace [267] has countered this claim and suggested that indeed the disk can serve this role. There are also more fundamental reservations with the Blandford–Znajek model, some of which are presented in [252, 155]. Such claims and counter-claims were for many years characteristic of the uncertainty in the theory of relativistic jets (see [157] for a discussion). However, direct numerical simulations may be helping to clarify the picture, as we discuss in Section 11.7. Plus, there is now observational evidence suggesting a possible connection between black hole spin and jet power, exactly as predicted by the Blandford–Znajek model [220], although again there are countering claims [93]