7 Advection-Dominated Accretion Flows (ADAFs)
The ADAF, or advection-dominated accretion flow, solution also involves advective cooling. In fact, it carries it to an extreme – nearly all of the viscously dissipated energy is advected into the black hole rather than radiated. Unlike the slim disk solution, which is usually invoked at high luminosities, the ADAF applies when the luminosity (and generally the mass accretion rate) are low. Because of their low efficiency, ADAFs are much less luminous than the Shakura–Sunyaev thin disks.
The solutions tend to be hot (close to the virial temperature), optically thin, and quasi-spherical (see
Figure 12 ). Their spectra are non-thermal, appearing as a power-law, often with a strong Compton
component. This makes them a good candidate for the Hard state observed in X-ray binaries (discussed in
Section 12.3).
). Their spectra are non-thermal, appearing as a power-law, often with a strong Compton
component. This makes them a good candidate for the Hard state observed in X-ray binaries (discussed in
Section 12.3).
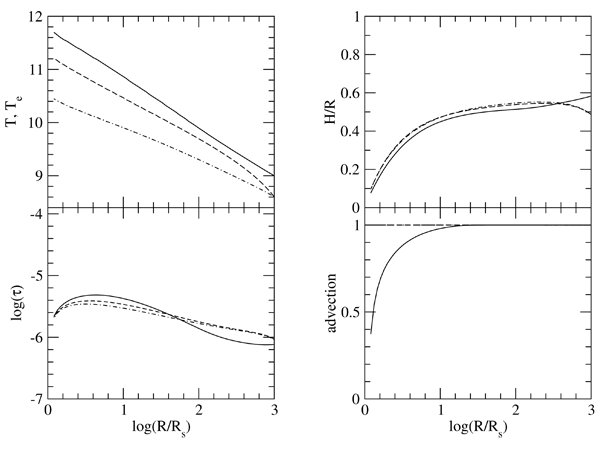
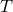 ADAF (solid lines). The
parameters are
ADAF (solid lines). The
parameters are 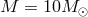 ,
, 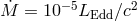 ,
, 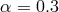 , and
, and 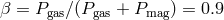 .
The outer boundary conditions are
.
The outer boundary conditions are 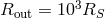 ,
, 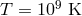 , and
, and 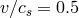 . Two-
. Two-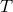 solutions with the same parameters and
solutions with the same parameters and 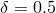 (dashed lines) and 0.01 (dot-dashed lines) are also
shown for comparison, where
(dashed lines) and 0.01 (dot-dashed lines) are also
shown for comparison, where 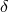 is the fraction of the turbulent viscous energy that directly heats
the electrons. Image reproduced by permission from [321], copyright by AAS.
is the fraction of the turbulent viscous energy that directly heats
the electrons. Image reproduced by permission from [321], copyright by AAS. ADAFs were formally introduced in the Newtonian limit through a series of papers by Narayan and
Yi [223, 224 , 225
, 225 ], followed closely by Abramowicz [6
], followed closely by Abramowicz [6 , 7] and others [106], although the existence of this
solution had been hinted at much earlier [134, 257]. In the same spirit as we gave the equations for the
Novikov–Thorne solution in Section 5.3 for thin disks, we report the self-similar ADAF solution found by
Narayan and Yi [224]. Again we present the solution with the following scaling:
, 7] and others [106], although the existence of this
solution had been hinted at much earlier [134, 257]. In the same spirit as we gave the equations for the
Novikov–Thorne solution in Section 5.3 for thin disks, we report the self-similar ADAF solution found by
Narayan and Yi [224]. Again we present the solution with the following scaling: 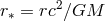 ,
,
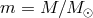 and
and 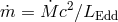 .
.
 is the radial infall velocity and
is the radial infall velocity and 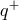 is the viscous dissipation of energy per unit volume. The
constants
is the viscous dissipation of energy per unit volume. The
constants 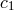 ,
, 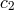 , and
, and 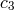 are given by
are given by
![(5 + 2 𝜖′) ′ c1 = --3α2---g(α, 𝜖) [ ′ ′ ]1∕2 c = 2𝜖(5-+-2𝜖-)g(α,𝜖′) 2 9α2 ′ c3 = 2(5 +-2𝜖)g(α, 𝜖′), 9α2](article618x.gif)
![( ) ′ -1-- 5-∕3 −-γg 𝜖 = fadv γg − 1 [ ]1∕2 ′ --18-α2--- g(α, 𝜖) ≡ 1 + (5 + 2𝜖′)2 − 1,](article619x.gif)
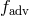 represents the fraction of viscously dissipated energy which is advected. The
remaining amount,
represents the fraction of viscously dissipated energy which is advected. The
remaining amount, 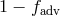 , is radiated locally.
, is radiated locally.
The rapid advection in ADAFs generally has two effects: 1) dissipated orbital energy can not be radiated
locally before it is carried inward and 2) the rotation profile is generally no longer Keplerian, although
Abramowicz [6] found solutions where the dominant cooling mechanism was advection, even when the
angular momentum profile was Keplerian. Fully relativistic solutions of ADAFs have also been found
numerically [13, 41]. Further discussion of ADAFs is given in the review article by Narayan and
McClintock [219 ].
].

![10 −1 −1∕2 v = [− 3.00 × 10 cm s ]αc1r ∗ , Ω = [2.03 × 105 s− 1]c m −1r− 3∕2, 2 20 2−2 ∗−1 cS = [9.00 × 10 cm s ]c3r∗ , ρ = [1.07 × 10−5 g cm −3]α −1c−1c−1∕2m −1m˙r −3∕2, 1 3 ∗ P = [9.67 × 1015 g cm −1 s−2]α−1c−1 1c13∕2m −1m˙r −∗5∕2, 8 − 1∕2 1∕2 −1∕2 1∕4 − 1∕2 1∕2 −5∕4 B = [4.93 × 10 G]α (1 − βm ) c1 c3 m m˙ r∗ , q+ = [2.94 × 1021 erg cm −3 s−1]𝜖′c13∕2m − 2 ˙mr −∗4, −1 −1 − 1∕2 τes = [1.75]α c1 m˙r ∗ , (101 )](article612x.gif)