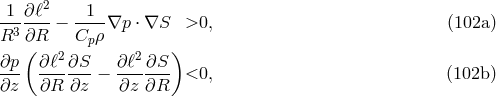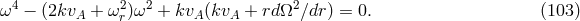8 Stability
Having reviewed some of the main analytic models of accretion disks, it is important now to discuss the issue of stability. Since all analytic models presume steady-state solutions, such models are only useful if the resulting solutions are stable. One reason to suspect accretion disks may not be stable is that the systematic differential rotation that is a signature feature of accretion is a potential source of energy, and therefore, of instability. Another is that some level of instability may be essential in accretion disks as it can provide a pathway to the kind of sustained turbulence anticipated by Shakura and Sunyaev (see Section 3.2.1).
8.1 Hydrodynamic stability
Within ideal hydrodynamics, local linear stability of an axisymmetric rotating flow is guaranteed if the Høiland criterion is satisfied [302]:
where 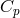 is the specific heat at constant pressure and
is the specific heat at constant pressure and 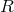 is the cylindrical radius (see [275] for the
criterion for relativistic stars). This criterion can be easily understood in two limits: For non-rotating
equilibria (e.g., a non-rotating star), the criterion reduces to the Schwarzschild criterion (
is the cylindrical radius (see [275] for the
criterion for relativistic stars). This criterion can be easily understood in two limits: For non-rotating
equilibria (e.g., a non-rotating star), the criterion reduces to the Schwarzschild criterion (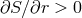 ) that
the entropy must not increase toward the interior (for stability against convection). Provided this is true,
local fluid elements will simply oscillate under stable buoyancy forces. To see the effects of rotation, we can
consider an equilibrium that has constant entropy everywhere. Then the Høiland criterion reduces
to the Rayleigh criterion (
) that
the entropy must not increase toward the interior (for stability against convection). Provided this is true,
local fluid elements will simply oscillate under stable buoyancy forces. To see the effects of rotation, we can
consider an equilibrium that has constant entropy everywhere. Then the Høiland criterion reduces
to the Rayleigh criterion (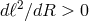 ): the specific angular momentum must not decrease
outward. Physically, if one perturbs a fluid element radially outward, it conserves its own specific
angular momentum. If the ambient specific angular momentum decreases outward, then the
fluid element will be rotating too fast to stay in its new position, and centrifugal forces will
push it further outward. Stability would be a fluid element that oscillates at the local epicyclic
frequency.
): the specific angular momentum must not decrease
outward. Physically, if one perturbs a fluid element radially outward, it conserves its own specific
angular momentum. If the ambient specific angular momentum decreases outward, then the
fluid element will be rotating too fast to stay in its new position, and centrifugal forces will
push it further outward. Stability would be a fluid element that oscillates at the local epicyclic
frequency.
As it turns out, the Høiland criterion is a huge disappointment for understanding why turbulence might exist in accretion disks. This is because it indicates that accretion disks with rotation profiles that do not differ too much from Keplerian should be strongly stable!
8.1.1 Papaloizou–Pringle Instability (PPI)
The Høiland criterion is only a local stability criterion. Flows can be locally stable, yet have
global instabilities. An example of this occurs in the Polish doughnut solution (Section 4).
Papaloizou and Pringle [238] showed that this solution is marginally stable with respect to local
axisymmetric perturbations yet unstable to low-order nonaxisymmetric modes. As with all
global instabilities, the existence of the Papaloizou–Pringle instability (PPI) is sensitive to
the assumed boundary conditions [44]. In cases where the disk overflows its potential barrier
(Roche lobe) and accretes through pressure-gradient forces across the cusp, the PPI is generally
suppressed [117 ].
].
8.1.2 Runaway instability
Another instability associated with the Polish doughnut is the runaway instability [5]. If matter is
overflowing its Roche lobe and accreting onto the black hole, then one of two evolutionary
tracks are possible: (i) As the disk loses material it contracts inside its Roche lobe, slowing the
mass transfer and resulting in a stable situation, or (ii) as the black hole mass grows, the cusp
moves deeper inside the disk, causing the mass transfer to speed up, leading to the runaway
instability. Recent numerical simulations show that, while this instability grows very fast, on
timescales of a few orbital periods, over a wide range of disk-to-black hole mass ratios when
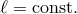 , i.e., a constant specific angular momentum profile [98], it is strongly suppressed whenever
the specific angular momentum of the disk increases with the radial distance as a power law,
, i.e., a constant specific angular momentum profile [98], it is strongly suppressed whenever
the specific angular momentum of the disk increases with the radial distance as a power law,
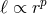 [63]. Even values of
[63]. Even values of 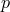 much smaller than the Keplerian limit (
much smaller than the Keplerian limit (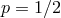 ) suffice to
suppress this particular instability. [This is equivalent to angular velocity profiles,
) suffice to
suppress this particular instability. [This is equivalent to angular velocity profiles, 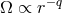 , with
, with
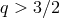 .]
.]
8.2 Magneto-rotational instability (MRI)
Although it had long been suspected that some sort of MHD instability might provide the necessary
turbulent stresses to make accretion work, the nature of this instability remained a mystery until the
rediscovery of the magneto-rotational instability by Balbus and Hawley [26, 118 , 27
, 27 ]. Originally discovered
by Velikhov [309], and generalized by Chandrasekhar [58], in the context of vertically magnetized Couette
flow between differentially rotating cylinders, the application of this instability to accretion disks was
originally missed.
]. Originally discovered
by Velikhov [309], and generalized by Chandrasekhar [58], in the context of vertically magnetized Couette
flow between differentially rotating cylinders, the application of this instability to accretion disks was
originally missed.
The instability itself can be understood through a simple mechanical model. Consider two particles of gas connected by a magnetic field line. Arrange the particles such that they are initially located at the same cylindrical distance from the black hole but with some vertical separation. Give one of the particles (say the upper one) a small amount of extra angular momentum, while simultaneously taking away a small amount of angular momentum from the lower one. The upper particle now has too much angular momentum to stay where it is and moves outward to a new radius. The lower particle experiences the opposite behavior and moves to a smaller radius. In the usual case where the angular velocity of the flow drops off with radius, the upper particle will now be orbiting slower than the lower one. Since these two particles are connected by a magnetic field line, the differing orbital speeds mean the field line will get stretched. The additional tension coming from the stretching of the field line provides a torque, which transfers angular momentum from the lower particle to the upper one. This just reinforces the initial perturbation, so the separation grows and angular momentum transfer is enhanced. This is the fundamental nature of the instability.
In more concrete terms, consider a disk threaded with a vertical magnetic field 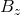 and having an
Alfvén speed
and having an
Alfvén speed 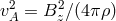 . The dispersion relation for perturbations of a fluid quantity
. The dispersion relation for perturbations of a fluid quantity
![δX ∼ exp [i(kz − ωt )]](article635x.gif) is [27
is [27 ]
]
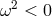 ), if and only if,
), if and only if, 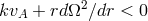 . Since
in accretion disks, the instability criteria can generally be met for weakly magnetized disks. More
specifically, the MRI exists for intermediate magnetic field strengths. In terms of the natural length scale of
the instability (
. Since
in accretion disks, the instability criteria can generally be met for weakly magnetized disks. More
specifically, the MRI exists for intermediate magnetic field strengths. In terms of the natural length scale of
the instability (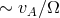 ), the field strength is constrained at the upper limit by the requirement that
the unstable MRI wavelength fit inside the vertical thickness of the disk (
), the field strength is constrained at the upper limit by the requirement that
the unstable MRI wavelength fit inside the vertical thickness of the disk (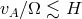 ). This
corresponds to field energy densities that are less than the thermal pressure, i.e.,
). This
corresponds to field energy densities that are less than the thermal pressure, i.e., 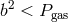 . At
the lower end, dissipative processes set a floor on the relevant length scales, and hence, field
strengths.
. At
the lower end, dissipative processes set a floor on the relevant length scales, and hence, field
strengths.
If the conditions for the instability are met, the fastest-growing mode, which dominates the early evolution, has the form of a “channel flow” involving alternating layers of inward- and outward-moving fluid. The amplitude of this solution grows exponentially until it becomes unstable to three-dimensional “parasitic modes” that feed off the gradients of velocity and magnetic field provided by the channel flow. The flow rapidly reaches a state of magnetohydrodynamic turbulence [118, 119]. This instability can be self-sustaining through a nonlinear dynamo process [52] – nonlinear because the motion that sustains or amplifies the magnetic field is driven by the field itself through the MRI. A more complete description of the linear and non-linear evolution of the MRI is provided in the review article by Balbus and Hawley [27]. A general relativistic linear analysis is presented in [20].
8.3 Thermal and viscous instability
It was realized by Shakura and Sunyaev themselves [280 ], as well as other authors [176
], as well as other authors [176 , 287], that the
Shakura–Sunyaev solution (Section 5.3) should be thermally and viscously unstable for disks in which
radiation pressure dominates (when the opacity is governed by electron scattering). The most
general and elegant arguments are presented in the classic paper by Piran [246
, 287], that the
Shakura–Sunyaev solution (Section 5.3) should be thermally and viscously unstable for disks in which
radiation pressure dominates (when the opacity is governed by electron scattering). The most
general and elegant arguments are presented in the classic paper by Piran [246 ]. This discovery
started a long debate, which continues unresolved to this day. A recent update is provided in
[60].
]. This discovery
started a long debate, which continues unresolved to this day. A recent update is provided in
[60].
To understand the thermal instability better, we consider a disk cooling through radiative diffusion. The
local emergent flux at radius  is given by
is given by
 is the radiation density constant,
is the radiation density constant, 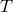 is a measure of the disk interior temperature, and
is a measure of the disk interior temperature, and 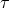 is
half the total vertical optical depth. If the opacity is dominated by electron scattering, then
is
half the total vertical optical depth. If the opacity is dominated by electron scattering, then
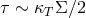 , where
, where 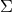 is the surface density of the disk, which is constant on the time scales of the
instabilities (very much less than the radial flow time scale). The Thomson opacity
is the surface density of the disk, which is constant on the time scales of the
instabilities (very much less than the radial flow time scale). The Thomson opacity 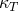 is also
constant, being independent of temperature, provided there is already sufficient ionization.
Therefore, the optical depth is independent of temperature and the cooling rate per unit area is
is also
constant, being independent of temperature, provided there is already sufficient ionization.
Therefore, the optical depth is independent of temperature and the cooling rate per unit area is
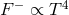 .
.
The dissipation rate per unit area is
Vertical hydrostatic equilibrium implies that the disk half thickness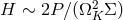 , so that Eq. (106
, so that Eq. (106 )
becomes
In the radiation pressure dominated inner region,
)
becomes
In the radiation pressure dominated inner region, 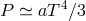 , so that Eq. (107
, so that Eq. (107 ) plus the
Shakura–Sunyaev assumption
) plus the
Shakura–Sunyaev assumption 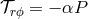 imply that
imply that 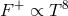 ! Hence a perturbative increase in
temperature increases both the local cooling and heating rates, but the heating rate increases much faster,
leading to a thermal runaway.
! Hence a perturbative increase in
temperature increases both the local cooling and heating rates, but the heating rate increases much faster,
leading to a thermal runaway.
Note, though, that this argument only applies when the viscous stress is proportional to the total
pressure 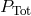 (
(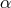 being the proportionality constant). For some time it seemed that a plausible
way to avoid this instability was to argue that the stress is proportional instead to the gas
pressure
being the proportionality constant). For some time it seemed that a plausible
way to avoid this instability was to argue that the stress is proportional instead to the gas
pressure 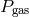 . Recent numerical simulations, though, of the magneto-rotational instability in
radiation-pressure dominated disks have shown that the stress is, in fact, proportional to the
total pressure [128
. Recent numerical simulations, though, of the magneto-rotational instability in
radiation-pressure dominated disks have shown that the stress is, in fact, proportional to the
total pressure [128 ]. Interestingly, these simulations exhibit no sign of the predicted thermal
instability.
]. Interestingly, these simulations exhibit no sign of the predicted thermal
instability.
Most observations also argue against the existence of this instability. In the case of accretion onto black
holes, the instability is supposed to set in for luminosities in excess of 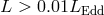 . However, during
outbursts, many stellar-mass black hole sources cross this limit both during their rise to peak luminosity
and on their decline to quiescence, showing no dramatic symptoms (although they do undergo state
changes, as described in Section 12.3). On the contrary, observations suggest that disks in black hole X-ray
binaries are stable up to at least
. However, during
outbursts, many stellar-mass black hole sources cross this limit both during their rise to peak luminosity
and on their decline to quiescence, showing no dramatic symptoms (although they do undergo state
changes, as described in Section 12.3). On the contrary, observations suggest that disks in black hole X-ray
binaries are stable up to at least 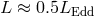 [80]. Certainly there is no evidence for the sensational
behavior anticipated by some models [172, 300].
[80]. Certainly there is no evidence for the sensational
behavior anticipated by some models [172, 300].