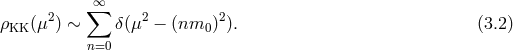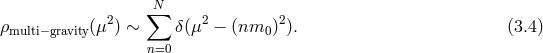3 Higher-Dimensional Scenarios
As seen in Section 2.5, the ‘most natural’ non-linear extension of the Fierz–Pauli mass term bears a ghost. Constructing consistent theories of massive gravity has actually been a challenging task for years, and higher-dimensional scenario can provide excellent frameworks for explicit realizations of massive gravity. The main motivation behind relying on higher dimensional gravity is twofold:- The five-dimensional theory is explicitly covariant.
- A massless spin-2 field in five dimensions has five degrees of freedom which corresponds to the correct number of dofs for a massive spin-2 field in four dimensions without the pathological BD ghost.
While string theory and other higher dimensional theories give rise naturally to massive gravitons, they usually include a massless zero-mode. Furthermore, in the simplest models, as soon as the first massive mode is relevant so is an infinite tower of massive (Kaluza–Klein) modes and one is never in a regime where a single massive graviton dominates, or at least this was the situation until the Dvali–Gabadadze–Porrati model (DGP) [208*, 209*, 207*], provided the first explicit model of (soft) massive gravity, based on a higher-dimensional braneworld model.
In the DGP model the graviton has a soft mass in the sense that its propagator does not have a simple
pole at fixed value 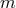 , but rather admits a resonance. Considering the Källén–Lehmann
spectral representation [331, 374], the spectral density function
, but rather admits a resonance. Considering the Källén–Lehmann
spectral representation [331, 374], the spectral density function 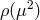 in DGP is of the form
in DGP is of the form
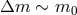 about
about
 .
.
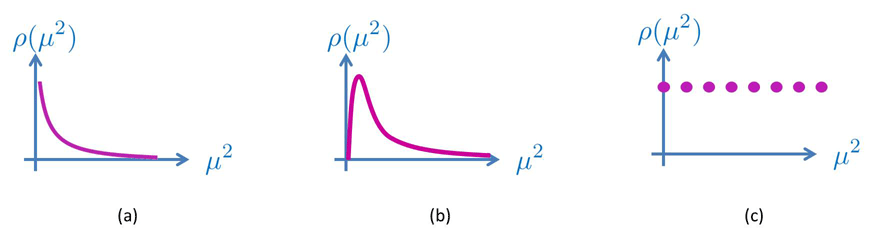
In a Kaluza–Klein decomposition of a flat extra dimension we have, on the other hand, an infinite tower of massive modes with spectral density function
We shall see in the section on deconstruction (5) how one can truncate this infinite tower by performing a discretization in real space rather than in momentum space à la Kaluza–Klein, so as to obtain a theory of a single massive graviton or a theory of multi-gravity (with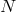 -interacting gravitons),
In this language, bi-gravity is the special case of multi-gravity where
-interacting gravitons),
In this language, bi-gravity is the special case of multi-gravity where 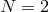 . These different
spectral representations, together with the cascading gravity extension of DGP are represented in
Figure 1*.
. These different
spectral representations, together with the cascading gravity extension of DGP are represented in
Figure 1*.
Recently, another higher dimensional embedding of bi-gravity was proposed in Ref. [495]. Rather than performing a discretization of the extra dimension, the idea behind this model is to consider a two-brane DGP model, where the radion or separation between these branes is stabilized via a Goldberger-Wise stabilization mechanism [255] where the brane and the bulk include a specific potential for the radion. At low energy the mass spectrum can be truncated to a massless mode and a massive mode, reproducing a bi-gravity theory. However, the stabilization mechanism involves a relatively low scale and the correspondence breaks down above it. Nevertheless, this provides a first proof of principle for how to embed such a model in a higher-dimensional picture without discretization and could be useful to tackle some of the open questions of massive gravity.
In what follows we review how five-dimensional gravity is a useful starting point in order to generate consistent four-dimensional theories of massive gravity, either for soft-massive gravity à la DGP and its extensions, or for hard massive gravity following a deconstruction framework.
The DGP model has played the role of a precursor for many developments in modified and massive gravity and it is beyond the scope of this review to summarize all of them. In this review we briefly summarize the DGP model and some key aspects of its phenomenology, and refer the reader to other reviews (see for instance [232, 390, 234]) for more details on the subject.
In this section, 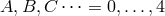 represent five-dimensional spacetime indices and
represent five-dimensional spacetime indices and
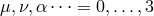 label four-dimensional spacetime indices.
label four-dimensional spacetime indices. 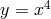 represents the fifth additional
dimension,
represents the fifth additional
dimension, 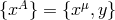 . The five-dimensional metric is given by
. The five-dimensional metric is given by 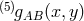 while the
four-dimensional metric is given by
while the
four-dimensional metric is given by 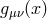 . The five-dimensional scalar curvature is
. The five-dimensional scalar curvature is ![(5) R [G ]](article391x.gif) while
while
![R = R [g]](article392x.gif) is the four-dimensional scalar-curvature. We use the same notation for the Einstein tensor where
is the four-dimensional scalar-curvature. We use the same notation for the Einstein tensor where
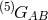 is the five-dimensional one and
is the five-dimensional one and 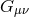 represents the four-dimensional one built out of
represents the four-dimensional one built out of
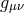 .
.
When working in the Einstein–Cartan formalism of gravity, 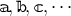 label five-dimensional Lorentz
indices and
label five-dimensional Lorentz
indices and 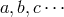 label the four-dimensional ones.
label the four-dimensional ones.

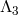 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity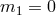
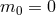 )
)