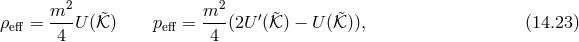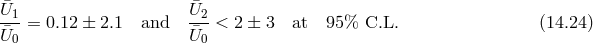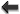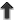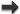14 Lorentz-Violating Massive Gravity
14.1 SO(3)-invariant mass terms
The entire analysis performed so far is based on assuming Lorentz invariance. In what follows we briefly review a few other potentially viable theories of massive gravity where Lorentz invariance is broken and their respective cosmology.
Prior to the formulation of the ghost-free theory of massive gravity, it was believed that no Lorentz
invariant theories of massive gravity could evade the BD ghost and Lorentz-violating theories were
thus the best hope; we refer the reader to [438*] for a thorough review on the field. A thorough
analysis of Lorentz-violating theories of massive gravity was performed in [200*] and more recently
in [107*]. See also Refs. [236, 73, 114] for other complementary studies. Since this field has
been reviewed in [438*] we only summarize the key results in this section (see also [74] for a
more recent review on many developments in Lorentz violating theories.) See also Ref. [378] for
an interesting spontaneous breaking of Lorentz invariance in ghost-free massive gravity using
three scalar fields, and Ref. [379] for a 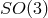 -invariant ghost-free theory of massive gravity
which can be formulated with three Stückelberg scalar fields and propagating five degrees of
freedom.
-invariant ghost-free theory of massive gravity
which can be formulated with three Stückelberg scalar fields and propagating five degrees of
freedom.
In most theories of Lorentz-violating massive gravity, the 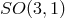 Poincaré group is broken down to
a
Poincaré group is broken down to
a 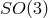 rotation group. This implies the presence of a preferred time. Preferred-frame effects are,
however, strongly constrained by solar system tests [487] as well as pulsar tests [54], see also [494, 493] for
more recent and even tighter constraints.
rotation group. This implies the presence of a preferred time. Preferred-frame effects are,
however, strongly constrained by solar system tests [487] as well as pulsar tests [54], see also [494, 493] for
more recent and even tighter constraints.
At the linearized level the general mass term that satisfies this rotation symmetry is
where space indices are raised and lowered with respect to the flat spatial metric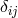 . This extends the
Lorentz invariant mass term presented in (2.39*). In the rest of this section, we will establish the analogue of
the Fierz–Pauli mass term (2.44*) in this Lorentz violating case and establish the conditions on the different
mass parameters
. This extends the
Lorentz invariant mass term presented in (2.39*). In the rest of this section, we will establish the analogue of
the Fierz–Pauli mass term (2.44*) in this Lorentz violating case and establish the conditions on the different
mass parameters 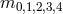 .
.
We note that Lorentz invariance is restored when 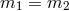 ,
, 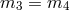 and
and 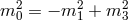 . The
Fierz–Pauli structure then further fixes
. The
Fierz–Pauli structure then further fixes 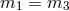 implying
implying 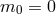 , which is precisely what
ensures the presence of a constraint and the absence of BD ghost (at least at the linearized
level).
, which is precisely what
ensures the presence of a constraint and the absence of BD ghost (at least at the linearized
level).
Out of these five mass parameters some of them have a direct physical meaning [200*, 437*, 438*]
- The parameter
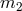 is the one that represents the mass of the helicity-2 mode. As a result we
should impose
is the one that represents the mass of the helicity-2 mode. As a result we
should impose 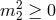 to avoid tachyon-like instabilities. Although we should bear in mind
that if that mass parameter is of the order of the Hubble parameter today
to avoid tachyon-like instabilities. Although we should bear in mind
that if that mass parameter is of the order of the Hubble parameter today 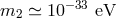 ,
then such an instability would not be problematic.
,
then such an instability would not be problematic.
- The parameter
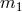 is the one responsible for turning on a kinetic term for the two helicity-1
modes. Since
is the one responsible for turning on a kinetic term for the two helicity-1
modes. Since 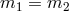 in a Lorentz-invariant theory of massive gravity, the helicity-1 mode
cannot be turned off (
in a Lorentz-invariant theory of massive gravity, the helicity-1 mode
cannot be turned off (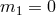 ) while maintaining the graviton massive (
) while maintaining the graviton massive (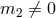 ). This is
a standard result of Lorentz invariant massive gravity seen so far where the helicity-1 mode is
always present. For Lorentz breaking theories the theory is quite different and one can easily
switch off at the linearized level the helicity-1 modes in a theory of Lorentz-breaking massive
gravity. The absence of a ghost in the helicity-1 mode requires
). This is
a standard result of Lorentz invariant massive gravity seen so far where the helicity-1 mode is
always present. For Lorentz breaking theories the theory is quite different and one can easily
switch off at the linearized level the helicity-1 modes in a theory of Lorentz-breaking massive
gravity. The absence of a ghost in the helicity-1 mode requires 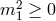 .
.
- If
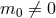 and
and 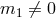 and
and 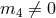 then two scalar degrees of freedom are present already
at the linear level about flat space-time and one of these is always a ghost. The absence of
ghost requires either
then two scalar degrees of freedom are present already
at the linear level about flat space-time and one of these is always a ghost. The absence of
ghost requires either 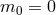 or
or 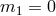 or finally
or finally 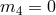 and
and 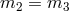 .
.
In the last scenario, where
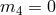 and
and 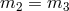 , the scalar degree of freedom loses its
gradient terms at the linear level, which means that this mode is infinitely strongly coupled
unless no gradient appears fully non-linearly either.
, the scalar degree of freedom loses its
gradient terms at the linear level, which means that this mode is infinitely strongly coupled
unless no gradient appears fully non-linearly either.
The case
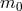 has an interesting phenomenology as will be described below. While it propagates
five degrees of freedom about Minkowski it avoids the vDVZ discontinuity in an interesting
way.
has an interesting phenomenology as will be described below. While it propagates
five degrees of freedom about Minkowski it avoids the vDVZ discontinuity in an interesting
way.
Finally, the case
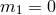 (including when
(including when 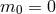 ) will be discussed in more detail in what
follows. It is free of both scalar (and vector) degrees of freedom at the linear level about
Minkowski and thus evades the vDVZ discontinuity in a straightforward way.
) will be discussed in more detail in what
follows. It is free of both scalar (and vector) degrees of freedom at the linear level about
Minkowski and thus evades the vDVZ discontinuity in a straightforward way.
- The analogue of the Higuchi bound was investigated in [72*]. In de Sitter with constant curvature
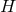 , the generalized Higuchi bound is
while if instead
, the generalized Higuchi bound is
while if instead 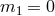 then no scalar degree of freedom are propagating on de Sitter
either so there is no analogue of the Higuchi bound (a scalar starts propagating on FLRW
solutions but it does not lead to an equivalent Higuchi bound either. However, the absence of
tachyon and gradient instabilities do impose some conditions between the different mass
parameters).
then no scalar degree of freedom are propagating on de Sitter
either so there is no analogue of the Higuchi bound (a scalar starts propagating on FLRW
solutions but it does not lead to an equivalent Higuchi bound either. However, the absence of
tachyon and gradient instabilities do impose some conditions between the different mass
parameters).
As shown in the case of the Fierz–Pauli mass term and its non-linear extension, one of the most natural way to follow the physical degrees of freedom and their health is to restore the broken symmetry with the appropriate number of Stückelberg fields.
In Section 2.4 we reviewed how to restore the broken diffeomorphism invariance using four Stückelberg
fields 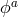 using the relation (2.75*). When Lorentz invariance is broken, the Stückelberg trick has to be
performed slightly differently. Performing an ADM decomposition, which is appropriate for the type of
Lorentz breaking we are considering, we can use for Stückelberg scalar fields
using the relation (2.75*). When Lorentz invariance is broken, the Stückelberg trick has to be
performed slightly differently. Performing an ADM decomposition, which is appropriate for the type of
Lorentz breaking we are considering, we can use for Stückelberg scalar fields 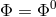 and
and
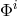 ,
, 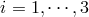 to define the following four-dimensional scalar, vector and tensors [107*]
to define the following four-dimensional scalar, vector and tensors [107*]
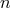 can be thought of as the ‘Stückelbergized’ version of the lapse and
can be thought of as the ‘Stückelbergized’ version of the lapse and 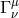 as that of the spatial
metric.
as that of the spatial
metric.
In the Lorentz-invariant case we are stuck with the combination 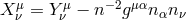 , but this
combination can be broken here and the mass term can depend separately on
, but this
combination can be broken here and the mass term can depend separately on 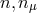 and
and 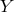 . This allows
for new mass terms. In [107*] this framework was derived and used to find new mass terms
that exhibit five degrees of freedom. This formalism was also developed in [200*] and used to
derive new mass terms that also have fewer degrees of freedom. We review both cases in what
follows.
. This allows
for new mass terms. In [107*] this framework was derived and used to find new mass terms
that exhibit five degrees of freedom. This formalism was also developed in [200*] and used to
derive new mass terms that also have fewer degrees of freedom. We review both cases in what
follows.
14.2 Phase 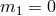
14.2.1 Degrees of freedom on Minkowski
As already mentioned, the helicity-1 mode have no kinetic term at the linear level on Minkowski if
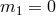 . Furthermore, it turns out that the field
. Furthermore, it turns out that the field  in (14.17*) is the Lagrange multiplier which removes
the BD ghost (as opposed to the field
in (14.17*) is the Lagrange multiplier which removes
the BD ghost (as opposed to the field 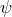 in the case
in the case 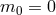 presented previously). It imposes the
constraint
presented previously). It imposes the
constraint 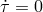 which in turns implies
which in turns implies 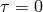 . Using this constraint back in the action, one can check
that there remains no time derivatives on any of the scalar fields, which means that there are no
propagating helicity-0 mode on Minkowski either [200*, 437*, 438*]. So in the case where
. Using this constraint back in the action, one can check
that there remains no time derivatives on any of the scalar fields, which means that there are no
propagating helicity-0 mode on Minkowski either [200*, 437*, 438*]. So in the case where 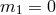 there are only 2 modes propagating in the graviton on Minkowski, the 2 helicity-2 modes as in
GR.
there are only 2 modes propagating in the graviton on Minkowski, the 2 helicity-2 modes as in
GR.
In this case, the absence of the ghost can be seen to follow from the presence of a residual symmetry on flat space [200*, 438*]
for three arbitrary functions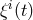 . In the Stückelberg language this implies the following internal
symmetry
. In the Stückelberg language this implies the following internal
symmetry
To maintain this symmetry non-linearly the mass term should be a function of 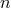 and
and 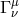 [438*]
[438*]
The absence of helicity-1 and -0 modes while keeping the helicity-2 mode massive makes this Lorentz violating theory of gravity especially attractive. Its cosmology was explored in [201] and it turns out that this theory of massive gravity could be a candidate for cold dark matter as shown in [202].
Moreover, explicit black hole solutions were presented in [438] where it was shown that in this theory of massive gravity black holes have hair and the Stückelberg fields (in the Stückelberg formulation of the theory) do affect the solution. This result is tightly linked to the fact that this theory of massive gravity admits instantaneous interactions which is generic to any action of the form (14.9*).
14.2.2 Non-perturbative degrees of freedom
Perturbations on more general FLRW backgrounds were then considered more recently in [72].
Unlike in Minkowski, scalar perturbations on curved backgrounds are shown to behave in a
similar way for the cases 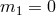 and
and 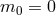 . However, as we shall see below, the case
. However, as we shall see below, the case
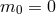 propagates five degrees of freedom including a helicity-0 mode that behaves as a scalar it
follows that on generic backgrounds the theory with
propagates five degrees of freedom including a helicity-0 mode that behaves as a scalar it
follows that on generic backgrounds the theory with 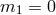 also propagates a helicity-0 mode.
The helicity-0 mode is thus infinitely strongly coupled when considered perturbatively about
Minkowski.
also propagates a helicity-0 mode.
The helicity-0 mode is thus infinitely strongly coupled when considered perturbatively about
Minkowski.
14.3 General massive gravity (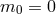 )
)
In [107*] the most general mass term that extends (14.1*) non-linearly was considered. It can be written using the Stückelberg variables defined in (14.3*), (14.4*) and (14.5*),
Generalizing the Hamiltonian analysis for this mass term and requiring the propagation of five degrees of freedom about any background led to the Lorentz-invariant ghost-free theory of massive gravity presented in Part II as well as two new theories of Lorentz breaking massive gravity. All of these cases ensures the absence of BD ghost by having 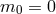 . The case where the BD ghost is
projected thanks to the requirement
. The case where the BD ghost is
projected thanks to the requirement 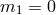 is discussed in Section 14.2.
is discussed in Section 14.2.
14.3.1 First explicit Lorentz-breaking example with five dofs
The first explicit realization of a consistent nonlinear Lorentz breaking model is as follows [107*]
with and where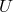 ,
, 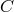 and
and 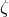 are scalar functions.
are scalar functions.
The fact that several independent functions enter the mass term will be of great interest for cosmology
as one of these functions (namely 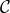 ) can be used to satisfy the Bianchi identity while the other function
can be used for an appropriate cosmological history.
) can be used to satisfy the Bianchi identity while the other function
can be used for an appropriate cosmological history.
The special case 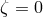 is what is referred to as the ‘minimal model’ and was investigated in [108*]. In
unitary gauge, this minimal model is simply
is what is referred to as the ‘minimal model’ and was investigated in [108*]. In
unitary gauge, this minimal model is simply
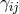 is the spatial part of the metric and
is the spatial part of the metric and 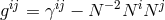 , where
, where 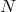 is the lapse and
is the lapse and 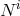 the shift.
the shift.
This minimal model is of special interest as both the primary and secondary second-class constraints that remove the sixth degree of freedom can be found explicitly and on the constraint surface the contribution of the mass term to the Hamiltonian is
where the overall factor is positive so the Hamiltonian is positive definite as long as the function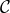 is
positive.
is
positive.
At the linearized level about Minkowski (which is a vacuum solution) this theory can be parameterized
in terms of the mass scales introduces in (14.1*) with 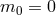 , so the BD ghost is projected out in a way
similar as in ghost-free massive gravity.
, so the BD ghost is projected out in a way
similar as in ghost-free massive gravity.
Interestingly, if 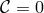 , this theory corresponds to
, this theory corresponds to 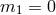 (in addition to
(in addition to 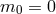 ) which as seen
earlier the helicity-1 mode is absent at the linearized level. However, they survive non-linearly and so the
case
) which as seen
earlier the helicity-1 mode is absent at the linearized level. However, they survive non-linearly and so the
case 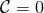 is infinitely strongly coupled.
is infinitely strongly coupled.
14.3.2 Second example of Lorentz-breaking with five dofs
Another example of Lorentz breaking 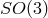 invariant theory of massive gravity was provided in [107*]. In
that case the Stückelberg language is not particularly illuminating and we simply give the form of the mass
term in unitary gauge (
invariant theory of massive gravity was provided in [107*]. In
that case the Stückelberg language is not particularly illuminating and we simply give the form of the mass
term in unitary gauge (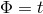 and
and 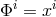 ),
),
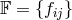 is the spatial part of the reference metric (for a Minkowski reference metric
is the spatial part of the reference metric (for a Minkowski reference metric 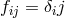 ),
),
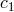 is a constant, and
is a constant, and 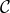 and
and 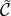 are functions of the spatial metric
are functions of the spatial metric 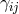 , while
, while 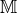 is a rank-3 matrix
which depends on
is a rank-3 matrix
which depends on 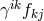 .
.
Interestingly, 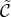 does not enter the Hamiltonian on the constraint surface. The contribution of this
mass term to the on-shell Hamitonian is [107]
does not enter the Hamiltonian on the constraint surface. The contribution of this
mass term to the on-shell Hamitonian is [107]
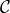 should be bounded from below
should be bounded from below
14.3.3 Absence of vDVZ and strong coupling scale
Unlike in the Lorentz-invariant case, the kinetic term for the Stückelberg fields does not only arise from the mixing with the helicity-2 mode.
When looking at perturbations about Minkowski and focusing on the scalar modes we can follow the analysis of [437*],
when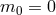
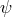 plays the role of the Lagrange multiplier for the primary constraint imposing
where
plays the role of the Lagrange multiplier for the primary constraint imposing
where  is the three-dimensional Laplacian. The secondary constraint then imposes the relation
where dots represent derivatives with respect to the time. Using these relations for
is the three-dimensional Laplacian. The secondary constraint then imposes the relation
where dots represent derivatives with respect to the time. Using these relations for  and
and 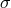 , we
obtain the Lagrangian for the remaining scalar mode (the helicity-0 mode)
, we
obtain the Lagrangian for the remaining scalar mode (the helicity-0 mode) 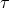 [437, 200],
In terms of power counting this means that the Lagrangian includes terms of the form
[437, 200],
In terms of power counting this means that the Lagrangian includes terms of the form 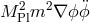 arising
from the term going as
arising
from the term going as 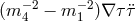 (where
(where 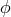 designates the helicity-0 mode which includes a
combination of
designates the helicity-0 mode which includes a
combination of 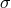 and
and  ). Such terms are not present in the Lorentz-invariant Fierz–Pauli case and its
non-linear ghost-free extension since
). Such terms are not present in the Lorentz-invariant Fierz–Pauli case and its
non-linear ghost-free extension since 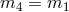 in that case, and they play a crucial role in this Lorentz
violating setting.
in that case, and they play a crucial role in this Lorentz
violating setting.
Indeed, in the small mass limit these terms 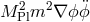 dominate over the ones that go as
dominate over the ones that go as 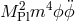 (i.e., the ones present in the Lorentz invariant case). This means that in the small mass limit, the correct
canonical normalization of the helicity-0 mode
(i.e., the ones present in the Lorentz invariant case). This means that in the small mass limit, the correct
canonical normalization of the helicity-0 mode 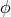 is not of the form
is not of the form 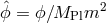 but rather
but rather
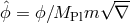 , which is crucial in determining the strong coupling scale and the absence of vDVZ
discontinuity:
, which is crucial in determining the strong coupling scale and the absence of vDVZ
discontinuity:
- The new canonical normalization implies a much larger strong coupling scale that goes as
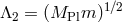 rather than
rather than 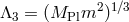 as is the case in DGP and ghost-free massive
gravity.
as is the case in DGP and ghost-free massive
gravity.
- Furthermore, in the massless limit the coupling of the helicity-0 mode to the tensor vanishes
fasters than some of the Lorentz-violating kinetic interactions in (14.20*) (which is scales as
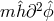 ). This means that one can take the massless limit
). This means that one can take the massless limit 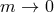 in such a way that the
coupling to the helicity-2 mode disappears and so does the coupling of the helicity-0 mode to
matter (since this coupling arises after de-mixing of the helicity-0 and -2 modes). This implies
the absence of vDVZ discontinuity in this Lorentz-violating theory despite the presence of five
degrees of freedom.
in such a way that the
coupling to the helicity-2 mode disappears and so does the coupling of the helicity-0 mode to
matter (since this coupling arises after de-mixing of the helicity-0 and -2 modes). This implies
the absence of vDVZ discontinuity in this Lorentz-violating theory despite the presence of five
degrees of freedom.
The absence of vDVZ discontinuity and the larger strong coupling scale 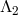 makes this theory more
tractable at small mass scales. We emphasize, however, that the absence of vDVZ discontinuity does prevent
some sort of Vainshtein mechanism to still come into play since the theory is still strongly coupled at the
scale
makes this theory more
tractable at small mass scales. We emphasize, however, that the absence of vDVZ discontinuity does prevent
some sort of Vainshtein mechanism to still come into play since the theory is still strongly coupled at the
scale 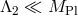 . This is similar to what happens for the Lorentz-invariant ghost-free theory of massive
gravity on AdS (see Section 8.3.6 and [154]). Interestingly, however, the same redressing of the strong
coupling scale as in DGP or ghost-free massive gravity was explored in [109*] where it was shown that in the
vicinity of a localized mass, the strong coupling scale gets redressed in such a way that the weak
field approximation remains valid till the Schwarzschild radius of the mass, i.e., exactly as in
GR.
. This is similar to what happens for the Lorentz-invariant ghost-free theory of massive
gravity on AdS (see Section 8.3.6 and [154]). Interestingly, however, the same redressing of the strong
coupling scale as in DGP or ghost-free massive gravity was explored in [109*] where it was shown that in the
vicinity of a localized mass, the strong coupling scale gets redressed in such a way that the weak
field approximation remains valid till the Schwarzschild radius of the mass, i.e., exactly as in
GR.
In these theories, bounds on the graviton comes from the exponential decay in the Yukawa potential
which switches gravity off at the graviton’s Compton wavelength, so the Compton wavelength ought to be
larger than the largest gravitational bound states which are of about 5 Mpc, putting a bound on the
graviton mass of 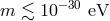 in which case
in which case 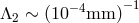 [108, 257].
[108, 257].
14.3.4 Cosmology of general massive gravity
The cosmology of general massive gravity was recently studied in [109*] and we summarize their results in what follows.
In Section 12, we showed how the Bianchi identity in ghost-free massive gravity prevents the existence
of spatially flat FLRW solutions. The situation is similar in general Lorentz violating theories of massive
gravity unless the function 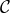 in (14.11*) is chosen so as to satisfy the following relation when the shift and
in (14.11*) is chosen so as to satisfy the following relation when the shift and
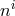 vanish [109*]
vanish [109*]
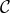 which satisfies the appropriate condition to allow for FLRW solutions, the
Friedmann equation then depends entirely on the function
which satisfies the appropriate condition to allow for FLRW solutions, the
Friedmann equation then depends entirely on the function 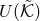 also defined in (14.11*). In this case the
graviton potential (14.10*) acts as an effective ‘dark fluid’ with respective energy density and pressure
dictated by the function
also defined in (14.11*). In this case the
graviton potential (14.10*) acts as an effective ‘dark fluid’ with respective energy density and pressure
dictated by the function 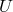 [109*]
leading to an effective phantom-like behavior when
[109*]
leading to an effective phantom-like behavior when 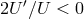 .
.
This solution is stable and healthy as long as the second derivative of 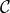 satisfies some conditions
which can easily be accommodated for appropriate functions
satisfies some conditions
which can easily be accommodated for appropriate functions 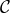 and
and 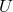 .
.
Expanding 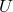 in terms of the scale factor for late time
in terms of the scale factor for late time 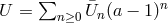 one can
use CMB and BAO data from [2] to put constraints on the first terms of that series [109*]
one can
use CMB and BAO data from [2] to put constraints on the first terms of that series [109*]
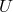 ,
see [109] for more details.
,
see [109] for more details.

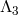 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
 )
)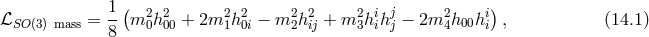
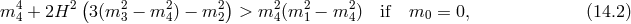
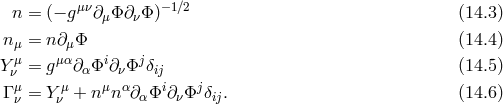


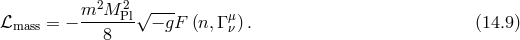
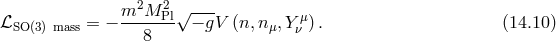
![[ ] V1(n,n μ,Yνμ) = n −1 n + ζ(Γ ) U(𝒦&tidle;) + n−1𝒞(Γ ), (14.11 )](article2749x.gif)
![( ) n2n μnα &tidle;𝒦μν = |( Γ μα − [--------]2-|) ∂αΦi ∂νΦjδij, (14.12 ) n + ζ(Γ )](article2750x.gif)
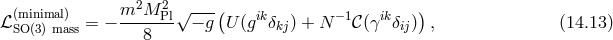
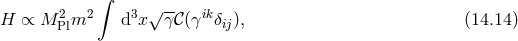
![[ ] V = c1 N⃗T (N 𝕀 + 𝕄 )− 1(𝔽 + N − 1𝕄 𝔽)(N 𝕀 + 𝕄 )−1 ⃗N (14.15 ) 2 2 + 𝒞 + N − 1𝒞 &tidle;.](article2771x.gif)
![∫ [ ] H ∝ M 2m2 d3x √ γ-− c1 ⃗N T (N 𝕀 + 𝕄 )−1𝔽 𝕄 (N 𝕀 + 𝕄 )−1N⃗ + 𝒞 , (14.16 ) Pl 2](article2781x.gif)
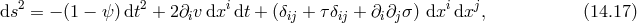


![2( [( ) ] 2 2 M--Pl -4- -4- m-2-−-m-3 2 ℒτ = 4 m24 − m21 ∇ τ − 3τ ¨τ − 2 m44 (∇ τ) (14.20 ) ( ) ) m22 2 2 + 4--2 − 1 τ ∇τ − 3m 2τ . (14.21 ) m 4](article2792x.gif)