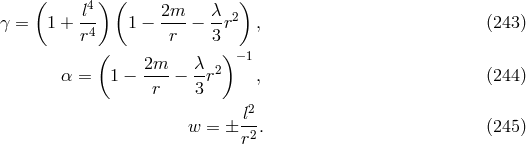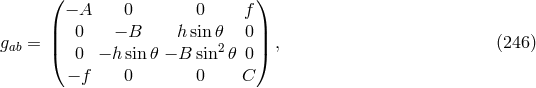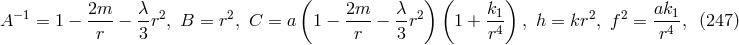8 Schrödinger II: Arbitrary Affine Connection
After an interruption of more than two years, in January 1946, the correspondence between Schrödinger and Einstein resumed; he sent Schrödinger two unpublished papers, among them his paper with E. Straus [179*].
“I am sending them to nobody else, because you are the only person known to me who is not wearing blinkers in regard to the fundamental questions in our science. The attempt depends on […] the introduction of a non-symmetric tensor as the only relevant field quantity […]. Pauli stuck out his tongue at me when I told him about it.” (quoted from [446*], p. 424.)
In his subsequent letter of 3 March 1946, Einstein pointed to a technical weakness of his theory: “the
non-symmetric tensor is not the most simple structure that is covariant with respect to the group, but
decomposes into the independently transforming parts 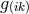 and
and ![g[ik]](article1010x.gif) ; the consequence of this
is that one can obtain a nondescript number of systems of second-order equations.” ([446*],
p. 424.)101
In both of the preceding papers ([147*, 179*]), Einstein had not given a single reference to any other
publication. Due to the the difficulties concerning transatlantic communication during the war years
1943 and 1944, Einstein possibly might not have seen Schrödinger’s six papers from 1943 and
1944.
; the consequence of this
is that one can obtain a nondescript number of systems of second-order equations.” ([446*],
p. 424.)101
In both of the preceding papers ([147*, 179*]), Einstein had not given a single reference to any other
publication. Due to the the difficulties concerning transatlantic communication during the war years
1943 and 1944, Einstein possibly might not have seen Schrödinger’s six papers from 1943 and
1944.
In April, Schrödinger had progressed with his research such that he could present its essence before the Irish Academy. In hindsight, he confessed to Einstein in a letter of 1 May 1946:
“One thing I do know is that my first work [P.R.I.A. 1943] was so imbecilic that it now is repellent to everyone, including you […]. This first work was no advance over ‘Einstein 1923’, but pretended to be.” ([446*], p. 426.)
M.-A. Tonnelat from Paris visited Schrödinger in Dublin during 1946 and, perhaps, discussions with
her had influenced him. Unlike what he had stated in his earlier paper when using a semi-metric connection
two years before [549*], Schrödinger now thought that: “[…] only the general case, dealt with here, is
completely satisfactory and gives new information” ([551*], 41). The “general case” meant: a general affine
connection, named 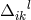 by him. After splitting it up into a symmetric part, the trace-free part
by him. After splitting it up into a symmetric part, the trace-free part 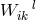 of
the torsion tensor
of
the torsion tensor 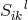 and vector torsion:
and vector torsion:
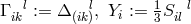 , and
, and 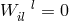 . Instead of the contractions of the curvature tensor (181*),
(182*) now
obtain. Again,
. Instead of the contractions of the curvature tensor (181*),
(182*) now
obtain. Again, 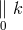 denotes covariant differentiation with respect to the symmetric connection
denotes covariant differentiation with respect to the symmetric connection 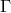 . The
quantities
. The
quantities 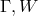 , and
, and 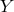 are varied independently. That
are varied independently. That 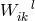 is tracefree is taken into account by help
of a multiplier term in the variational principle:
The Lagrangian density
is tracefree is taken into account by help
of a multiplier term in the variational principle:
The Lagrangian density 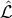 is demanded to be a functional of the two contractions (215*), (216*) of the
affine curvature tensor.The field variables
is demanded to be a functional of the two contractions (215*), (216*) of the
affine curvature tensor.The field variables 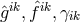 , and
, and 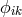 are introduced as they were in
Section 6.1.1 by (154*) and (159*). A decomposition of (215*) then leads to:
The field equations following from the variational principle (217*) with respect to variation of
are introduced as they were in
Section 6.1.1 by (154*) and (159*). A decomposition of (215*) then leads to:
The field equations following from the variational principle (217*) with respect to variation of 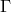 and
and 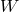 are similar to (189*):
The abbreviation, or rather definition of the vector density
are similar to (189*):
The abbreviation, or rather definition of the vector density 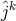 is as before (
is as before (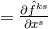 ) while
with102
) while
with102
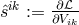 . The variation with respect to
. The variation with respect to 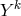 , after some calculation, led to the simple relation between
the current densities:
By the field equations, the dynamics of three fields were to be determined, gravitational, electromagnetic,
and mesonic field:
, after some calculation, led to the simple relation between
the current densities:
By the field equations, the dynamics of three fields were to be determined, gravitational, electromagnetic,
and mesonic field:
“Because the Lagrangian is left undetermined for the time being, each of the three fields
will be represented by two “conjugate” tensorial entities in the field equations, gravitation
by 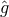 and
and  ; the skew fields by
; the skew fields by 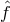 and
and 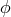 and by
and by 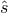 and
and 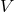 respectively.”([551*],
44.)
respectively.”([551*],
44.)
In order to arrive at equations better separated in the new fields, Schrödinger redefined the field variables by forming the linear combinations:
The equations for the Maxwellian field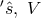 are claimed to then be “kept entirely aloof from the rest by
the remarkable fact that the
are claimed to then be “kept entirely aloof from the rest by
the remarkable fact that the 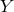 -vector drops out rigorously from all the other equations except
the last eqn. (216*)”. The fields
-vector drops out rigorously from all the other equations except
the last eqn. (216*)”. The fields 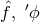 with the current density
with the current density 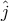 are related to the meson
field.
are related to the meson
field.
As in his earlier papers, a metric was introduced by (157*), i.e., via 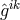 . Schrödinger then calculated
the expression for the symmetric part of the connection as in (191*) but now only in first approximation in
. Schrödinger then calculated
the expression for the symmetric part of the connection as in (191*) but now only in first approximation in
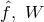 :
:
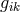 . Schrödinger did interpret (228*) as Proca
equation103
for the meson, “except for the term which contains explicitly second derivatives”. According to him, the
additional term was taking into account a slight direct influence of gravitation on the meson field ([551*],
47).
. Schrödinger did interpret (228*) as Proca
equation103
for the meson, “except for the term which contains explicitly second derivatives”. According to him, the
additional term was taking into account a slight direct influence of gravitation on the meson field ([551*],
47).
In the same approximation, Schrödinger also wrote down gravitational field equations looking like Einstein’s except for the fact that on the side of the matter tensor a number of geometrical objects do appear. They are said to describe the interaction of gravitational and electromagnetic fields as well as of gravitational and mesonic fields. A cosmological term could also be present.
Schrödinger’s conclusion was cautious:
“This encourages one to regard an affine connection of space-time as the competent geometrical interpretation (from the classical point of view) of the three physical tensor fields we know.” ([551*], p. 50)
He questioned, however, that the classical field laws would “be of much help in guessing the true quantum laws of the meson” if they were violently non-linear.
In his correspondence with Schrödinger, Einstein doubted that a theory using only the connection (i.e., without additional metric) be feasible. He reported about difficulties in his theory to solve for the connection as a function of the metric and its first derivative:
“We have squandered a lot of time on this thing, and the result looks like a gift from the devil’s grandmother.” ([446*], p. 426.)
In another letter of 16 July 1946 to Schrödinger, Einstein did explain the progress achieved “thanks to the truly great skill and persistence of my assistant Straus”, then published in [179*]. He also commented on conceptual differences. Schrödinger used the wave model for the transport of electromagnetic energy while Einstein thought this to be “really false on account of quantum actualities” ([446*], p. 427). Another of his correspondents, W. Pauli, also did not believe in purely affine theory. He wrote to him on the same day at which Schrödinger’s paper finally had been issued, i.e., on 21 November 1946:
“I personally am completely convinced – contrary to you as it seems – that for physics
nothing reasonable follows from the affine connection without metric. Palatini’s theorem
again slams the door. I also believe that each tensor, e.g., the contracted curvature tensor,
immediately must be split into a symmetric and a skew part* (* In general: tensors into
their irreducible symmetry classes), and to avoid every adding sign between them. What
God did separate, humans must not join.) ([489*], p. 401)”104
8.1 Schrödinger’s debacle
Schrödinger kept Einstein informed about his continuing work on UFT within affine geometry “[…] by reports at about fortnightly intervals” ([446*], p. 429). He had read the papers of Einstein, and Einstein & Straus [179*, 147*] from the previous two years. (Cf. Sections 7.2 and 7.3 above.) Now he again presented his newest development of the theory to the Royal Irish Academy on 27 January 1947. Believing that he had made a break-through, he had written to Einstein a day earlier:
“Today I can report on a real advance. […] In brief, the situation is this. If in the affine theory, which I have developed in general form in recent years, one takes the special, the only reasonable Lagrange function, namely the square root of the determinant of the Einstein tensor, then one obtains something fabulously good.” ([446*], p. 430.)
Well, this might have tasted a bit stale to Einstein because he had used this same Lagrangian about twenty five years ago [141*] and abandoned the theory, nonetheless! (cf. Section 4.3.2 of Part I.) To the exuberant Schrödinger a modest statement to the Academy would not do: the press was also invited. So, Schrödinger began:
“The nearer one approaches truth, the simpler things become. I have the honour of laying before you today the keystone of the Affine Field Theory and thereby the solution of a 30 year old problem: the competent generalization of Einstein’s great theory of 1915. The solution was
where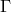 is the general affinity of 64 components. That is all. From these three lines my friends
would reconstruct the theory, supposing the paper I am handing in got hopelessly lost, and I
died on my way home.” ([446*], p. 430–432.)
is the general affinity of 64 components. That is all. From these three lines my friends
would reconstruct the theory, supposing the paper I am handing in got hopelessly lost, and I
died on my way home.” ([446*], p. 430–432.) In the paper submitted together with his presentation, the Lagrangian (229*) was given a factor 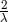 with
a real constant
with
a real constant 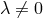 playing an important role ([552*], p. 164). Schrödinger first played its occurrence
down, unconvincingly though, by saying that it could be transformed to
playing an important role ([552*], p. 164). Schrödinger first played its occurrence
down, unconvincingly though, by saying that it could be transformed to 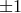 , but in his final field
equations, the constant stood for an additional “cosmological” term. In his own words (in a note “added in
proof”), his field equations “[…] include ‘the cosmological term’ without containing a cosmological constant.”
([552*], p. 171.)
, but in his final field
equations, the constant stood for an additional “cosmological” term. In his own words (in a note “added in
proof”), his field equations “[…] include ‘the cosmological term’ without containing a cosmological constant.”
([552*], p. 171.)
The presentation to the Academy and the press did not contain the finer details. For this kind of public, he wrote down the field equations in the reduced form:105
with his “star”-connection (cf. (27*)) while the complete equations in his paper are: where if vector torsion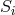 is used. Equation (233*) expresses nothing but the vanishing of the
is used. Equation (233*) expresses nothing but the vanishing of the 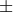 -derivative of
-derivative of
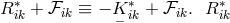 (
(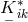 ) is formed with the “star”-connection. The (asymmetric) metric
again was defined as a variational derivative with respect to
) is formed with the “star”-connection. The (asymmetric) metric
again was defined as a variational derivative with respect to 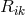 . By some manipulation of the formalism,
Schrödinger was able to show that (233*) is equivalent to the slightly generalized weak field equations of
Einstein & Straus (206*) – (208*) (cf. below, Section 7.3):
. By some manipulation of the formalism,
Schrödinger was able to show that (233*) is equivalent to the slightly generalized weak field equations of
Einstein & Straus (206*) – (208*) (cf. below, Section 7.3):
Schrödinger was well aware of this:
“We now have to endorse the remarkable fact, that the actual content of equations
[(236*) – (237*) …] differs from the theory presented in Einstein’s two papers, quoted above,
(i.e., [147*, 179*]) only by formal 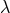 -terms.106
His theory amounts to putting
-terms.106
His theory amounts to putting  in (236*) – (237*). There is a formal difference in
that he, from the outset, regards all skew tensors as purely imaginary. […]” ([552*], p. 167.)
in (236*) – (237*). There is a formal difference in
that he, from the outset, regards all skew tensors as purely imaginary. […]” ([552*], p. 167.)
Equations (235*) to (237*) were also called the “para-form” of his field equations [526*]. They may be
seen as 18 equations for the 16 field variables 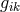 . According to Schrödinger: “The surplus
of 2 equations is vindicated by two trivial identities, one between the first members of (237*),
and one between those of (236*).” (236*) is not a definition, such as it was used by Eddington
(cf. Section 4.3.1 of Part I) but derived from the Lagrangian (229*), the definition in (157*) and:
. According to Schrödinger: “The surplus
of 2 equations is vindicated by two trivial identities, one between the first members of (237*),
and one between those of (236*).” (236*) is not a definition, such as it was used by Eddington
(cf. Section 4.3.1 of Part I) but derived from the Lagrangian (229*), the definition in (157*) and:
Schrödinger also confessed that “it may turn out that I have overrated the practical advantage of (233*) over (235*) – (237*).”
The Irish Press caught the bait: “Twenty persons heard and saw history being made in the world of physics yesterday as they sat in the lecture hall of the Royal Irish Academy, Dublin, and heard Dr. Erwin Schrödinger. […] It was later told me that the theory should express everything in field physics.” ([446*], p. 432.) The news spread quickly; the science editor of The New York Times sent Schrödinger’s statement and a copy of his paper to Einstein, and asked him for a comment. In the text supplied by Einstein which became also widely distributed, he said:
“Schrödinger’s latest effort […] can be judged only on the basis of mathematical-formal qualities, but not from the point of view of ‘truth’ (i.e., agreement with the facts of experience). Even from this point of view I can see no special advantages over the theoretical possibilities known before, rather the opposite. […] It seems undesirable to me to present such preliminary attempts to the public in any form.” ([446*], p. 432–433.)
Schrödinger must have had second thoughts about his going public; he tried to justify himself vis-à-vis Einstein – although he had not yet seen Einstein’s rebuff. In his letter, he admitted to have indulged “in a little hot air […] I blew myself up quite a bit. […] This thing is being done for the purpose of obtaining cheap and fraudulent publicity for a discredited administration.” His excuse was that he had tried by this “commotion” to increase his salary and to bring the authorities to reach a decision whether his wife, as a widow, could get a pension or not ([446*], p. 433). Einstein replied coolly and curtly:
“I was not correct in my objection to your Hamilton-function. But your theory does not really differ from mine, only in the presentation and in the ‘cosmological term’ which mine lacks. […] Not your starting-point but your equations permit a transition to vanishing cosmological constant, then the content of your theory becomes identical with mine” ([446*], p. 434),
and stopped writing to Schrödinger for the next three years. Pauli seemingly had followed the events from Switzerland and wrote to Schrödinger calmly on 9 February 1947:
“Many thanks for your interesting letter of 26. Jan. I would have liked to only respond
to it after your first enthusiasm about the new field equations will have given place to a
more sober judgment (perhaps the letter is written still too early). Of course, progress is
made by your decision to take a specific Lagrangian; also, the mathematical side of your
thoughts to me seems extraordinarily clear. Nevertheless, my reservations with regard to a
non-irreducible object as a basis continue unabatedly. […]” ([489*], p. 415).107
He then expressed in more detail, why for him, only irreducible tensors are the variables to be used. He emphasized that he was not against the “logical possibility” of Schrödinger’s field equations, but could not accept their “necessity and naturalness”. According to Pauli, already before “the next few years”, it would become clear whether these field equations “have something to do with physics, or not.” In a letter to Sommerfeld of 31 October 1947, Pauli agreed with Sommerfeld’s “negative opinion concerning Einstein’s present physics” and supported them with much the same arguments as those given to Schrödinger ([489*], p. 475).
As to the physical interpretation of the geometrical objects in his “ultimate” theory, Schrödinger
associated the two skew-symmetric fields ![[ik] ˆg , ℱik](article1077x.gif) as contravariant density and covariant field tensor,
so that (234*), and (233*), or (235*) amount to (modified) Maxwell equations. The quantities
as contravariant density and covariant field tensor,
so that (234*), and (233*), or (235*) amount to (modified) Maxwell equations. The quantities
![√ --- √ --- √ --- g[ik], − ggirgksℱrs, − ggrigskℱrs, 12 − g(grigks − grkgis)ℱrs](article1078x.gif) ) were assumed to be linked to “electric
charge, mesonic charge and matter”.
) were assumed to be linked to “electric
charge, mesonic charge and matter”.
“We must not forget, that we are here faced with a truly unitary theory, in which we have to expect all fields to coalesce into an inseparable union, almost as close as that of the electric and magnetic field entailed by Restricted Relativity.” ([552*], p. 169.)
The episode differs from Einstein’s repeated claims to have found the final unified field theory, in the 1920s and 30s, in that Einstein did not have to call in the press, and in fact was clever enough not do so. However, his friends in the press were covering his work to the extent, that for each new publication he received the same public attention as Schrödinger in this single case – staged by himself. By his public reaction to Schrödinger, Einstein solidified his position as the opinion leader in research concerning UFT.
8.2 Recovery
Schrödinger must have been depressed after so much self-confidence! To a friend he had written:
“I have found the unitary field equations. They are based on primitive affine geometry, […] Albert did the main job in 1923, but missed the goal by a hair’s breadth. The result is fascinatingly beautiful. I could not sleep a fortnight without dreaming of it.” ([256], p. 168)108
The report of L. Bass that: “After a farcical debacle […], Schrödinger put away the material in a file
labeled despondently ‘Die Einstein Schweinerei’ (the Einstein mess)” ([13], p. 120) describes only a
momentary halt. After a pause of almost one year, Schrödinger continued his publishing in this
topic, i.e., UFT. As a beginning, he surveyed the possibilities for the construction of UFT in a
whole class of geometries descending “from the theory of gravitation in empty space by very
natural and straightforward generalization without any further artifice.” ([555*], p. 205.) He
distinguished between the three cases: metrical, affine and mixed geometry depending on whether
only 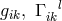 , or both can be regarded as independent variables. As a Lagrangian he took
, or both can be regarded as independent variables. As a Lagrangian he took
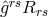 , with as before
, with as before 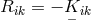 . The further classification depended on additional symmetry
conditions on the basic variable(s). He dismissed the case of a non-symmetric metric and symmetric
connection “since there is no simple and natural clue” by which the Levi-Civita connection should be
replaced. It was perhaps this remark which induced J. I. Horváth to suggest “a selection
principle for the final theory in the case of the affine theories”, to wit: the field equations must be
invariant against changes of the affinities which preserve the parallelism [284]. He derived such
transformations (changes) from the weakened condition for auto-parallels (cf. Section 2.1.1,
after (22*)) and arrived, without noting it, at Einstein’s
. The further classification depended on additional symmetry
conditions on the basic variable(s). He dismissed the case of a non-symmetric metric and symmetric
connection “since there is no simple and natural clue” by which the Levi-Civita connection should be
replaced. It was perhaps this remark which induced J. I. Horváth to suggest “a selection
principle for the final theory in the case of the affine theories”, to wit: the field equations must be
invariant against changes of the affinities which preserve the parallelism [284]. He derived such
transformations (changes) from the weakened condition for auto-parallels (cf. Section 2.1.1,
after (22*)) and arrived, without noting it, at Einstein’s 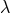 -transformations (52*) introduced
before.
-transformations (52*) introduced
before.
In commenting Schrödinger’s work on affine field theories, Pauli also contributed to UFT, if only
in a letter to Pascual Jordan of 13 July 1948. Once more he criticized the use of reducible
tensors by Schrödinger, notably of the Ricci tensor 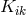 instead of its symmetric
instead of its symmetric 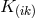 and
skew symmetric
and
skew symmetric ![K[ik]](article1085x.gif) parts, separately. He then derived the “mathematically simplest scalar
densities” as building elements of the Lagrangian. If a symmetric connection is used, they are given
by109
parts, separately. He then derived the “mathematically simplest scalar
densities” as building elements of the Lagrangian. If a symmetric connection is used, they are given
by109
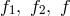 . Pauli’s conclusion was:
. Pauli’s conclusion was:
“Even if we try to specialize these functions by simplifying arguments, a lot of arbitrariness
remains. The impression prevails that the basic geometrical concepts have nothing to do
with physics. Einstein did express it like this: ‘the action function then is obtained by
leering at another sheet of paper lying next to it, and on which the formulae for another
theory can be seen.’ ” ([489*], p. 541–542).110
Schrödinger was still convinced of his approach to unified field theory. In a paper of 1951, he showed a pragmatic attitude: He set out to solve approximately the field equations with asymmetric metric and asymmetric connection111:
He argued that:
“[…] an assiduous application of such methods to weak fields is bound to tell us something on the interlacing of three things, gravitational field, electromagnetic field, and electric charges, all three of which spring from one basic conception. […] One may hope that this will provide a better foundation to the quantum mechanical treatment of fields, which at present is based on a number of classical or pseudo-classical field theories of independent origin, cemented together by interaction terms’.” ([558*], p. 555.)
As a result he claimed that “a pure charge-free Maxwellian field of radiation is capable of producing a
gravitational field which according to the old theory could only be produced by matter other
than an electromagnetic field.” By this, the non-vanishing of the trace of a correspondingly
defined energy-momentum tensor is meant. He also offered three alternatives for an energy
(pseudo-) tensor which all vanish for a single plane wave. As to physical interpretations, ![kij = g[ij]](article1091x.gif) is identified with the electromagnetic field with the space-space components standing for the
electrical field. The magnetic 4-current vanishes in consequence of the field equations while the
electrical 4-current is added by hand and given by the expression
is identified with the electromagnetic field with the space-space components standing for the
electrical field. The magnetic 4-current vanishes in consequence of the field equations while the
electrical 4-current is added by hand and given by the expression 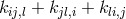 . Despite
Schrödinger’s going beyond the linear approximation up to quadratic terms, the “[…] influence of both
fields [i.e., gravitational and electromagnetic] on the motion of the charges and that of the
gravitational field on the electromagnetic” was missing. Thus, the paper contained no new fundamental
insights.
. Despite
Schrödinger’s going beyond the linear approximation up to quadratic terms, the “[…] influence of both
fields [i.e., gravitational and electromagnetic] on the motion of the charges and that of the
gravitational field on the electromagnetic” was missing. Thus, the paper contained no new fundamental
insights.
A favorable reaction came from a young Harvard mathematician R. L. Ingraham who was an assistant
to Oswald Veblen in Princeton at the Institute for Advanced Studies in 1953. He set out to rewrite the field
equations of Schrödinger’s affine unified theory [552*, 555*] in “a more physically meaningful form” [305*].
He assumed 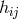 to represent gravitation but found the direct link of the skew-symmetric part of
to represent gravitation but found the direct link of the skew-symmetric part of
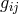 with the electromagnetic field as incorrect. By an elementary calculation presented a year
later also by M.-A. Tonnelat (cf. [627*] or the table on p. 15 of [632*]), Eq. (33*) is put into the
form:112
with the electromagnetic field as incorrect. By an elementary calculation presented a year
later also by M.-A. Tonnelat (cf. [627*] or the table on p. 15 of [632*]), Eq. (33*) is put into the
form:112
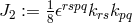 . This equation then is rewritten as one of the usual Maxwell equations (in a space
with metric
. This equation then is rewritten as one of the usual Maxwell equations (in a space
with metric 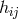 ) with a complicated r.h.s. which then is made to vanish by the additional assumptions
that
) with a complicated r.h.s. which then is made to vanish by the additional assumptions
that 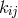 is a curl,
is a curl, 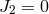 , and
, and 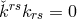 . Likewise, an additional condition was laid on the curvature
tensor (cf. his Eq. (27a), p. 749) such that the field equation reduced to the Einstein vacuum equation
with cosmological constant. That de Sitter space is a solution of Ingraham’s equations with
. Likewise, an additional condition was laid on the curvature
tensor (cf. his Eq. (27a), p. 749) such that the field equation reduced to the Einstein vacuum equation
with cosmological constant. That de Sitter space is a solution of Ingraham’s equations with 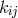 representing some sort of plane wave, is unsurprising. Fortunately, this naive strategy of imposing
additional conditions with the aim to obtain interpretable field equations, did not have many
followers.
representing some sort of plane wave, is unsurprising. Fortunately, this naive strategy of imposing
additional conditions with the aim to obtain interpretable field equations, did not have many
followers.
8.3 First exact solutions
The first to derive several genuine exact, spherically symmetric and static (sss) solutions of
Schrödinger’s field equations with cosmological constant (235*) – (237*) in 1947 was his research
assistant A. Papapetrou [475*]. His ansatz
contained five unknown functions of the radial coordinate 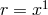 (
(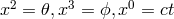 ):
):
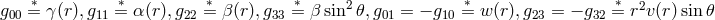 . In the paper,
he treated the cases
. In the paper,
he treated the cases 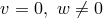 and
and 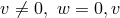 real. After setting
real. After setting 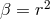 in the first case,
integration of the field equations led to
in the first case,
integration of the field equations led to
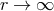 ,
, 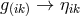 . Thus, if
. Thus, if
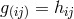 is interpreted as the space-time metric (gravitational field tensor),
is interpreted as the space-time metric (gravitational field tensor), ![g = k [ij] ij](article1112x.gif) as the
electromagnetic field tensor, then a deviation from the Reissner–Nordström–de Sitter-solution
of general relativity with
as the
electromagnetic field tensor, then a deviation from the Reissner–Nordström–de Sitter-solution
of general relativity with 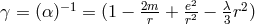 was obtained. Introducing the
elementary electric charge by
was obtained. Introducing the
elementary electric charge by 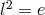 , the source term for the point charge in (243*) shows the wrong
radial dependence, although from (243*) we must conclude that a radial electromagnetic field is
present.113
The solution does not describe the Coulomb field. At this point, this seems no serious objection to the
theory, because other static spherically symmetric (SSS) solution might exist. However, cf. Section 9.6,
where the most general sss solution is given.
In the second case,
, the source term for the point charge in (243*) shows the wrong
radial dependence, although from (243*) we must conclude that a radial electromagnetic field is
present.113
The solution does not describe the Coulomb field. At this point, this seems no serious objection to the
theory, because other static spherically symmetric (SSS) solution might exist. However, cf. Section 9.6,
where the most general sss solution is given.
In the second case,  is replaced by
is replaced by 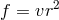 and only a particular solution with
and only a particular solution with
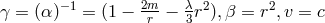 , with
, with  a constant was reached by Papapetrou. Thus, the
radial electromagnetic field is constant. Moreover, this constant electric field does not influence
the gravitational field. Papapetrou also discussed approximate solutions and concluded for
them that
a constant was reached by Papapetrou. Thus, the
radial electromagnetic field is constant. Moreover, this constant electric field does not influence
the gravitational field. Papapetrou also discussed approximate solutions and concluded for
them that 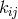 does not describe the electromagnetic field but the electromagnetic potential.
This would rule out an interpretation of the solution in terms of an electric field. All these
solutions would not have been acceptable to Einstein (in the sense of describing sources of
electricity), because they were not free of singularities. Unlike for the gravitational field in general
relativity or the electromagnetic field, for the “total” field in UFT singularities were no longer
permitted:
does not describe the electromagnetic field but the electromagnetic potential.
This would rule out an interpretation of the solution in terms of an electric field. All these
solutions would not have been acceptable to Einstein (in the sense of describing sources of
electricity), because they were not free of singularities. Unlike for the gravitational field in general
relativity or the electromagnetic field, for the “total” field in UFT singularities were no longer
permitted:
“As I’ve said, one does’t get away without singularities in the case of Maxwell’s equations.
But no reasonable person believes that Maxwell’s equations can hold rigorously. They are,
in suitable cases, first approximations for weak fields. It is now my belief that, for a serious
and rigorous field theory, one must insist that the field be free of singularities everywhere.”
([116*], p. 93)114
We shall come back to the demand that exact solutions ought to be free of singularities in Sections 9.6.2 and 10.3.2.
For static metrics, Papapetrou was able to extend a result of Einstein [145*], and Einstein & W. Pauli [177*] to the strong field equations of Einstein’s UFT: non-singular static metrics of the strong field equations of UFT which would represent the (gravitational) field of a non-vanishing mass do not exist [474*]. Note that this result depends on the identification of the symmetric part of the metric with the gravitational field (potential). A year later, a different proof was given by E. Straus for the weak field equations. In the same paper, Straus concluded: “There exists no static centrally symmetric solution of the field equations which is asymptotically flat and regular throughout” ([592*], p. 420). For A. Lichnerowicz’ contribution to the problem of Einstein & Pauli cf. Section 10.5.1.
H. Takeno and two coworkers of the Hiroshima Institute for Theoretical physics also took up the search
for exact solutions with spherical symmetry of Einstein’s and Schrödinger’s field equations [602*]. Except
for a different notation and an assumed time-dependency, the form of the metric was the same as
Papapetrou’s; it contained five free functions 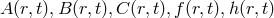 (and the usual
coordinates
(and the usual
coordinates  ):
):
Two types of solutions according to which 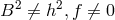 (type I), or
(type I), or 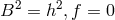 (type II) were
distinguished. And then, immediately, the time-dependence of the free functions was dropped.
Assuming in addition
(type II) were
distinguished. And then, immediately, the time-dependence of the free functions was dropped.
Assuming in addition 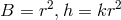 , the authors derived the general solution of type II
of Schrödinger’s field equations (the weak equations with cosmological constant
, the authors derived the general solution of type II
of Schrödinger’s field equations (the weak equations with cosmological constant 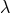 ) to be:
) to be:
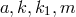 are integration constants. The solution generalized Papapetrou’s two exact static
solutions (
are integration constants. The solution generalized Papapetrou’s two exact static
solutions (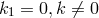 and
and 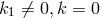 ) by “combining” them. Apparently, at the time the authors
did not know of Wyman’s earlier paper, also containing solutions with
) by “combining” them. Apparently, at the time the authors
did not know of Wyman’s earlier paper, also containing solutions with 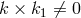 ; see Section 9.6.1. The
main conclusion drawn by Takeno et al. was that the fundamental equation (30*) has no unique solution if
; see Section 9.6.1. The
main conclusion drawn by Takeno et al. was that the fundamental equation (30*) has no unique solution if
![det(gab) = 2det(g(ab)), det(g[ab]) = 0](article1134x.gif) . This condition is consistent with (364*) derived by M.-A. Tonnelat;
cf. Section 10.2.3.
. This condition is consistent with (364*) derived by M.-A. Tonnelat;
cf. Section 10.2.3.
In his paper of 1951 discussed above in Section 8.2, Schrödinger expressed his disenchantment with regard to the search for exact solutions:
“One may hope that exact solutions, involving strong fields, will reveal the nature of the ultimate particles. I do not believe this, mainly because I do not believe the ultimate particles to be identifiable individuals that could be described in this fashion. Moreover, in the symmetric theory (i.e., in Einstein’s theory of 1916) the exact solutions, involving strong fields, have disclosed the ingenuity of the mathematicians who discovered them, but nothing more. […]” ([558*], p. 3)
In view of the research done since, e.g., on black holes or cosmology, the last sentence possibly would not be upheld by him, today.

![l l l l Δ ik = Γ ik + W ik + 2δ[iYk], (214 )](article1014x.gif)
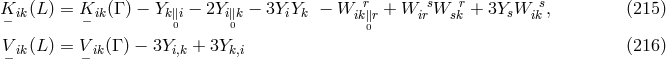
![∫ δ dτ[ℒˆ(K ik(L ),V lm (L )) + 2 pˆrW rss] = 0. (217 ) − −](article1023x.gif)
 =--[----k-− ---i--] − Y[i,k] − W ik∥r + 3YsW ik . (219 ) 2 ∂x ∂x 0](article1027x.gif)
![ˆgik + δk[ 1fˆis − gˆisY − 2rˆi ] + δi[ 1ˆfks − ˆgksY − 2ˆrk ] + 3gˆikY = 0, (220 ) ∥l l 3 ∥s s 3 l 3 ∥s s 3 l ik k 1 is is i 1 ks ks ik is k ks i fˆ ∥l − δl (3fˆ ∥s + fˆ Ys) + δl(3fˆ ∥s + ˆf Ys) + 3ˆf Yl + ˆg W sl − ˆg W sl = 0. (221 )](article1030x.gif)


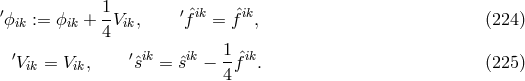
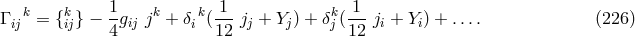
![l 1-ls 2- l W ik = − 2g (fks;i + fsi;k − fik;s) + 3 δ[ijk] + ..., (227 )](article1052x.gif)
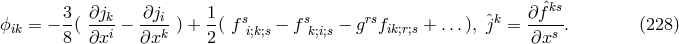
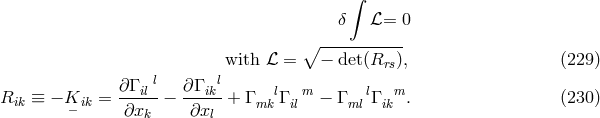
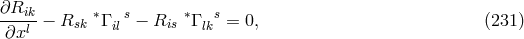
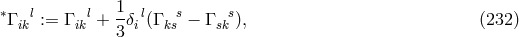
![∂[R-∗ik-+-ℱik] ∗ ∗ s ∗ ∗ s ∂xl − [R sk + ℱsk ] Γ il − [R is + ℱis] Γ lk = 0, (233 )](article1065x.gif)
![( ) 2- ∂-Γ k ∂-Γ i 4- ℱik := 3 ∂xi − ∂xk ≡ − 3S [i,k], (234 )](article1066x.gif)
![ˆg[is],s = 0, (235 ) ∗ R (ik) − λgik = 0, (236 ) (R ∗[ik] − λg[ik]),l + (R ∗[kl] − λg [kl]),i + (R∗[li] − λg [li]),k = 0. (237 )](article1072x.gif)

![∘ --------- ∘ -------------------------- H = det K , H = K K K K 𝜖ijkl𝜖pqrs, H = K K 𝜖ijkl. (239 ) 0 (ik) 1 (ip) (jq) [kr] [ls] 2 [ij] [kl]](article1086x.gif)
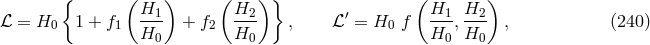
![g ik∥l = 0, L[iss] = 0, K ik = λgik. (241 ) +− −](article1090x.gif)
![[∘ -- √ -- ] h( hˇkrs + 1-√J2-𝜖rspqk ) = 0, (242 ) g 2 h pq ,s](article1095x.gif)