15 Research in Italy
15.1 Introduction
In previous sections, we already have encountered several contributions from Italian researchers. The publication
of the 3rd and 4th edition of Einstein’s The Meaning of Relativity in an Italian translation in 1950 and
1953268
seems to have given a boost to research on UFT in Italy. Bruno Finzi went about a fresh derivation of the field equations (287*) to
(290*). He started from the Lagrangian Einstein had used in the 4th Princeton edition of his
book [156*], i.e., 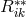 [cf. Section 2.3.2, Eq. (83*)]. However, he did not proceed by varying
Einstein’s Lagrangian with regard to the (asymmetric) metric but instead by varying its solenoidal
and irrotational parts, separately [201]. While arriving at the correct result, his method is no
less arbitrary than what Einstein had tried himself. As one of the major figures in research
in the geometry of relativity and unified theories, Finzi became a favoured reviewer of UFT
in Italy [473*, 202, 203*]. He made it very clear that the theory did not predict new empirical
facts: “Until now, no prevision of verifiable new physical facts have emerged from this unified
theory”,269
[cf. Section 2.3.2, Eq. (83*)]. However, he did not proceed by varying
Einstein’s Lagrangian with regard to the (asymmetric) metric but instead by varying its solenoidal
and irrotational parts, separately [201]. While arriving at the correct result, his method is no
less arbitrary than what Einstein had tried himself. As one of the major figures in research
in the geometry of relativity and unified theories, Finzi became a favoured reviewer of UFT
in Italy [473*, 202, 203*]. He made it very clear that the theory did not predict new empirical
facts: “Until now, no prevision of verifiable new physical facts have emerged from this unified
theory”,269 but remained a firm believer in Einstein’s unified theory:
but remained a firm believer in Einstein’s unified theory:
“The charm of this theory lies in its generality, its simplicity, and, let’s say it clearly, in its
beauty, attributes which the utmost Einsteinian synthesis possesses, more than any other
noted today.” ([473], p. 306)270
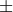 -derivatives; she also
studied alternative forms for the electromagnetic tensor (
-derivatives; she also
studied alternative forms for the electromagnetic tensor (![kij,R [ij]](article2723x.gif) , or its duals) in first and second
approximation according to the scheme (499*) given below [232, 233]. By adding a term to the
Einstein–Straus Lagrangian depending only on the metric tensor, F. de Simoni showed how to trivially
derive from a variational principle all the different systems of field equations of UFT including those
suggested by Bonnor, or Kursunŏglu (cf. Section 13.1) [115]. Laura Gotusso generalized a theory
suggested by Horváth with a Riemannian metric and the connection
, or its duals) in first and second
approximation according to the scheme (499*) given below [232, 233]. By adding a term to the
Einstein–Straus Lagrangian depending only on the metric tensor, F. de Simoni showed how to trivially
derive from a variational principle all the different systems of field equations of UFT including those
suggested by Bonnor, or Kursunŏglu (cf. Section 13.1) [115]. Laura Gotusso generalized a theory
suggested by Horváth with a Riemannian metric and the connection ![l l l Lik = L (ik) + F [i jk]](article2724x.gif) where
where 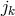 is the electrical current vector
is the electrical current vector 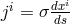 . The torsion vector thus is proportional to
the Lorenz force
. The torsion vector thus is proportional to
the Lorenz force 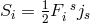 and the autoparallels describe the motion of a charged point
particle271
[285*]. Gotusso generalized Horváth’s theory by adding another tensor to the connection:
and the autoparallels describe the motion of a charged point
particle271
[285*]. Gotusso generalized Horváth’s theory by adding another tensor to the connection:
![Got l l l l L ik = L (ik) + F [i jk] + U ik](article2728x.gif) satisfying
satisfying 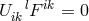 . With regard to this connection
. With regard to this connection 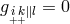 [231].
The Ricci tensor belonging to the connection introduced was not calculated.
[231].
The Ricci tensor belonging to the connection introduced was not calculated.
15.2 Approximative study of field equations
To P. Udeschini we owe investigations closer to physics.272 In a series of papers, he followed an approximative approach to the field equations of UFT by an expansion of the fundamental tensor starting from flat space:
where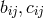 were assumed to be small of 1st and 2nd order. In linear approximation, the connection then
read [652] as:
whence follow the Eqs. (210*) and (211*) already obtained by Einstein and Straus. The field equations split
into two groups related either to the gravitational potential (
were assumed to be small of 1st and 2nd order. In linear approximation, the connection then
read [652] as:
whence follow the Eqs. (210*) and (211*) already obtained by Einstein and Straus. The field equations split
into two groups related either to the gravitational potential (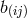 ) or to the electromagnetic field
) or to the electromagnetic field
![Fij ∼ b[ij]](article2738x.gif) . In the identification by Udeschini, i.e.,
. In the identification by Udeschini, i.e., ![ijrs ij 𝜖 b[rs] =: ψF](article2739x.gif) , where
, where 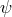 is a constant, the field
equations then were:
The coordinate conditions
is a constant, the field
equations then were:
The coordinate conditions 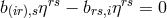 was used. In this approximation, the current density,
was used. In this approximation, the current density,
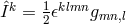 satisfies
satisfies 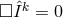 .
In 2nd approximation ([653, 654, 657]), (500*) is replaced by:
For
.
In 2nd approximation ([653, 654, 657]), (500*) is replaced by:
For 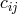 , the field equations lead to an inhomogeneous wave equation
, the field equations lead to an inhomogeneous wave equation 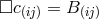 with a lengthy
expression for
with a lengthy
expression for 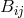 built up from products of
built up from products of 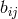 and
and 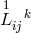 as well as squares of
as well as squares of 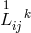 . Further
equations are
. Further
equations are ![c[ir],sηrs = Ni](article2752x.gif) and
and ![□ 𝜖klmnc [mn ],l = 𝜖klmnB [mn ],l,](article2753x.gif) with
with 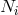 being a sum of
products of
being a sum of
products of 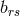 and
and 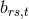 . For the electrical 4-current density, in 2nd approximation [658]
. For the electrical 4-current density, in 2nd approximation [658]
![2 □ Ik = 2𝜖klmnηrsηpqb[rm],p(b(sn),ql − b(nq),sl)](article2757x.gif) . As a result, in the 2nd approximation the field equations for
the gravitational and electromagnetic fields now intertwine. From his more general approach, Udeschini
then reproduced the special case Schrödinger had treated in 1951 [558], i.e.,
. As a result, in the 2nd approximation the field equations for
the gravitational and electromagnetic fields now intertwine. From his more general approach, Udeschini
then reproduced the special case Schrödinger had treated in 1951 [558], i.e., ![b(ij) = 0,c[ij] = 0](article2758x.gif) : An
electromagnetic field, small of first order, generates a gravitational field small of second order. The
reciprocal case, i.e., a gravitational field small of first order cannot influence an electromagnetic field of
second order [655].
: An
electromagnetic field, small of first order, generates a gravitational field small of second order. The
reciprocal case, i.e., a gravitational field small of first order cannot influence an electromagnetic field of
second order [655].
From this approximative approach, Udeschini calculated an additional term for the shift of the frequency
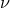 of a spectral line by the unified field due to
of a spectral line by the unified field due to 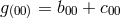 with
with 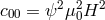 and
and 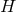 the polar
magnetic field:
the polar
magnetic field:
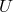 is the Newtonian gravitational potential [656, 659*, 660*]. This result depends crucially on the
interpretations for the gravitational and electromagnetic fields. If, in place of
is the Newtonian gravitational potential [656, 659*, 660*]. This result depends crucially on the
interpretations for the gravitational and electromagnetic fields. If, in place of 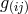 , the quantity
, the quantity 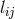 is
chosen to describe the gravitational field (potential), then the 2nd term with the magnetic field drops
out of (503*) ([660], p. 446). Due to this and to further ambiguities, it makes no sense to test
(503*); at best, the constant
is
chosen to describe the gravitational field (potential), then the 2nd term with the magnetic field drops
out of (503*) ([660], p. 446). Due to this and to further ambiguities, it makes no sense to test
(503*); at best, the constant 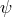 eventually needed for other experiments could be determined.
eventually needed for other experiments could be determined.
L. Martuscelli studied the assignment of the electromagnetic tensor 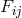 to the quantity
to the quantity ![R [ij]](article2769x.gif) [389].
In first approximation,
[389].
In first approximation, ![1 Fij = 2□b [ij]](article2770x.gif) , while in second approximation
, while in second approximation
![A [ij]](article2772x.gif) again containing derivatives of products of
again containing derivatives of products of 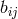 and
and 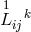 and of
products of
and of
products of 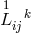 . A. Zanella wrote down a formal scheme of field equations which in any order n of the
approximation looked the same as in the 2nd order field equations. The r.h.s. term in, e.g.,
. A. Zanella wrote down a formal scheme of field equations which in any order n of the
approximation looked the same as in the 2nd order field equations. The r.h.s. term in, e.g., 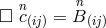 contains combination of quantities obtained in all previous orders. Convergence was not shown
[723].
contains combination of quantities obtained in all previous orders. Convergence was not shown
[723].
15.3 Equations of motion for point particles
While Einstein refused to accept particles as singularities of the unified field, E. Clauser, P. Udeschini, and C. Venini in Italy followed Infeld (cf. Section 9.3.3) by assuming the field equations of UFT to hold only outside the sources of mass and charge treated as singularities:
“In the equations for the unified field, no energy-tensor has been introduced: only the
external problem outside the sources of the unified field (masses and charges), assumed to
be singularities, exists” ([659], p. 74).273
As mentioned in Section 10.3.2, Emilio Clauser (1917 – 1986) used the method of Einstein & Infeld in
order to derive equations of motion for point particles. In [81], he had obtained an integral formula
for a 2-dimensional surface integral surrounding the singularities. With its help, Clauser was
able to show that from Einstein’s weak field equations for two or more “particles” all classical
forces in gravitation and electromagnetism (Newton, Coulomb, and Lorentz) could be obtained
[82]. In his interpretation, 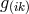 stood for the gravitational,
stood for the gravitational, ![g[ik]](article2778x.gif) for the electromagnetic
field.
for the electromagnetic
field.
He expanded the fundamental tensor according to:
where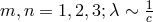 with the vacuum-velocity of light
with the vacuum-velocity of light
 .274
In the
.274
In the 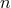 -th step of approximation, the field equations are:
In the symmetrical part of the fundamental tensor, only terms beginning with
-th step of approximation, the field equations are:
In the symmetrical part of the fundamental tensor, only terms beginning with 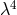 contribute, in the
skew-symmetric part terms from
contribute, in the
skew-symmetric part terms from 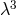 on. The Newtonian and Coulomb forces exerted on on a “particle“
from the others, appear in the terms
on. The Newtonian and Coulomb forces exerted on on a “particle“
from the others, appear in the terms 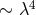 together with a force independent of distance and not
containing the masses of the “particles“. After laborious calculations, the Lorentz force showed up in the
terms
together with a force independent of distance and not
containing the masses of the “particles“. After laborious calculations, the Lorentz force showed up in the
terms 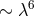 . This result is the very least one would have expected from UFT: to reproduce the effects of
general relativity and of electrodynamics.
. This result is the very least one would have expected from UFT: to reproduce the effects of
general relativity and of electrodynamics.
In a subsequent paper by Clauser, Einstein’s weak system for the field equations of UFT was developed in every order into a recursive Maxwell-type system for six 3-vectors corresponding to electric and magnetic fields and intensities, and to electric and magnetic charge currents [83]. Quasi-stationarity for the fields was assumed.
C. Venini expanded the weak field equations by help of the formalism generated by Clauser and calculated
the components of the fundamental tensor 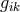 , or rather of
, or rather of 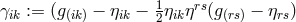 ,
directly up to 2nd approximation:
,
directly up to 2nd approximation: 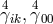 , and
, and 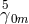 [672]. He applied it to calculate the inertial mass in
2nd approximation and obtained the corrections of special and general relativity; unfortunately the
contribution of the electrostatic field energy came with a wrong numerical factor [673]. He also calculated
the field of an electrical dipole in 2nd approximation [674]. Moreover, again by use of Clauser’s equation of
motion, Venini derived the perihelion precession for a charged point particle in the field of a second one. It
depends on both the charges and masses of the particles. However, his formula is not developed as far
as that it could have been used for an observational test [675]. In hindsight, it is astonishing
how many exhausting calculations Clauser and Venini dedicated to determining the motion of
point particles in UFT in view of the ambiguity in the interpretation and formulation of the
theory.
[672]. He applied it to calculate the inertial mass in
2nd approximation and obtained the corrections of special and general relativity; unfortunately the
contribution of the electrostatic field energy came with a wrong numerical factor [673]. He also calculated
the field of an electrical dipole in 2nd approximation [674]. Moreover, again by use of Clauser’s equation of
motion, Venini derived the perihelion precession for a charged point particle in the field of a second one. It
depends on both the charges and masses of the particles. However, his formula is not developed as far
as that it could have been used for an observational test [675]. In hindsight, it is astonishing
how many exhausting calculations Clauser and Venini dedicated to determining the motion of
point particles in UFT in view of the ambiguity in the interpretation and formulation of the
theory.



![□b = 0, □b = 0, b ηrs = 0. (501 ) (ij) [ij] [ir],s](article2741x.gif)
![2 1 1 1 1 1 L ijk = L ijk + -ηkr(crj,i + cir,j − cji,r) − ηkr(b[sj]L rsi + b[is]L jrs+ b(rs)Lijs ). (502 ) 2](article2745x.gif)

![1 1 Fij = -□b [ij] +--□c[ij] + A [ij] (504 ) 2 2](article2771x.gif)
![2k 2k 2k g00 = 1 + Σk=1 λ α g 00, g(mn ) = − δmn + Σk=1 λ2kα2k 2gk(mn), k g[mn ] = Σk=1 λ2kβ2k g[mn], 2k+1 g(0m ) = Σk=1 λ2k+1α2k+1 g (0m), (505 ) 2k+1 2k+1 2k+1 g[0m ] = Σk=1 λ β g [0m ], (506 )](article2779x.gif)
![n n n n n r R (ik) = 0, R[ik],l + R [kl],i + R [li],k = 0, L[ir] = 0. (507 )](article2787x.gif)