17 Alternative Geometries
Although a linear theory of gravitation can be derived as a first approximation of Einstein–Schrödinger-type theories ([641*], pp. 441–446), the results may be interpreted not only in UFT, but also in the framework of “alternative” theories of gravitation. Nevertheless, M.-A. Tonnelat remained defensive with respect to her linear theory:
“ […] this theory does not pursue the hidden aim of substituting general relativity but
of exploring in a rather heuristic way some specifically tough and complex domains
resulting from the adoption of the principles of a non-Euclidean theory […]”. ([382],
p. 327)293
We will now describe theories with a different geometrical background than affine or mixed geometry and its linearized versions.
17.1 Lyra geometry
In Lyra geometry, the notion of gauge transformation is different from its use in Weyl geometry. Coordinate
and gauge transformations are given the same status: they are defined without a metric or a connection
[386, 531]. A reference system now consists of two elements: Besides the usual coordinate transformations
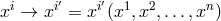 a gauge transformation
a gauge transformation 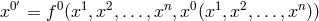 with
gauge function
with
gauge function 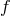 is introduced. The subgroup of coordinate transformations is given by those
transformations for which
is introduced. The subgroup of coordinate transformations is given by those
transformations for which 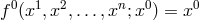 . A change of the reference system implies both
coordinate and gauge transformations. Tangent vectors
. A change of the reference system implies both
coordinate and gauge transformations. Tangent vectors 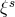 under a change of coordinates and gauge
transform like:
under a change of coordinates and gauge
transform like:
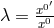 is the gauge factor (Lyra’s “Eichverhältnis”); a basis of tangential space is given by
is the gauge factor (Lyra’s “Eichverhältnis”); a basis of tangential space is given by
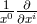 ; a 1-form basis would be
; a 1-form basis would be 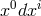 . The metric then is introduced by
. The metric then is introduced by 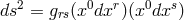 , and
the asymmetric connection
, and
the asymmetric connection 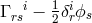 is defined via
Here, similar to Weyl’s theory, an arbitrary 1-form
is defined via
Here, similar to Weyl’s theory, an arbitrary 1-form 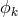 appears and the demand that the length of a
transported vector be conserved leads to
with the Christoffel symbol calculated from
appears and the demand that the length of a
transported vector be conserved leads to
with the Christoffel symbol calculated from 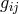 . The curvature tensor is defined by
Hence the curvature scalar becomes
. The curvature tensor is defined by
Hence the curvature scalar becomes 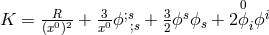 where the semicolon denotes covariant derivation with regard to
where the semicolon denotes covariant derivation with regard to 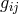 , and
, and
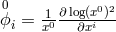 .294
In the thesis of D. K. Sen, begun with G. Lyra in Göttingen and finished in Paris with M.-A. Tonnelat,
the field equations are derived from the Lagrangian
.294
In the thesis of D. K. Sen, begun with G. Lyra in Göttingen and finished in Paris with M.-A. Tonnelat,
the field equations are derived from the Lagrangian 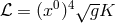 . In the gauge
. In the gauge 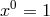 , they are given
by [571]:
Weyl’s field equations in a special gauge are the same – apart from the cosmological term
, they are given
by [571]:
Weyl’s field equations in a special gauge are the same – apart from the cosmological term 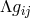 . The
problem with the non-integrability of length-transfer does not occur here. For further discussion of Lyra
geometry cf. [572].
. The
problem with the non-integrability of length-transfer does not occur here. For further discussion of Lyra
geometry cf. [572].
In relying on a weakened criterion for a theory to qualify as UFT suggested by Horváth (cf. Section 19.1.1), after he had added the Lagrangian for the electromagnetic field, Sen could interpret his theory as unitary. In later developments of the theory by him and his coworkers in the 1970s, it was interpreted just as an alternative theory of gravitation (scalar-tensor theory) [573, 574, 310]. In both editions of his book on scalar-tensor theory, Jordan mentioned Lyra’s “modification of Riemannian geometry which is close to Weyl’s geometry but different from it” ([319], p. 133; ([320], p. 154).
17.2 Finsler geometry and unified field theory
Already one year after Einstein’s death, G. Stephenson expressed his view concerning UFT:
“The general feeling today is that in fact the non-symmetric theory is not the correct
means for unifying the two fields.”295
In pondering how general relativity could be generalized otherwise, he criticized the approach by Moffat [439] and suggested an earlier attempt by Stephenson & Kilmister [591] starting from the line element [cf. (428*)]:
the geodesics of which correctly describe the Lorentz force. Since Riemann’s habilitation thesis, the possibility of more general line elements than those expressed by
bilinear forms was in the air. One of Riemann’s examples was “the fourth root of a quartic differential
expression” (cf. Clifford’s translation in [329], p. 113). Eddington had spoken of the space-time interval
depending “on a general quartic function of the 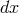 ’s” ([139], p. 11). Thus it was not unnatural that
K. Tonooka from Japan looked at Finsler spaces with fundamental form
’s” ([139], p. 11). Thus it was not unnatural that
K. Tonooka from Japan looked at Finsler spaces with fundamental form 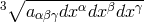 [648], except that only
[648], except that only 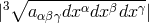 is an acceptable distance. With (551*), Stephenson
went along the route to Finsler (or even a more general) geometry which had been followed by
O. Varga [669*], by Horváth [283] and by Horváth & Moór, [286]. He mentioned the thesis of
E. Schaffhauser-Graf [530] to be discussed below. In Finsler geometry, the line element is dependent on
the direction of moving from the point with coordinates
is an acceptable distance. With (551*), Stephenson
went along the route to Finsler (or even a more general) geometry which had been followed by
O. Varga [669*], by Horváth [283] and by Horváth & Moór, [286]. He mentioned the thesis of
E. Schaffhauser-Graf [530] to be discussed below. In Finsler geometry, the line element is dependent on
the direction of moving from the point with coordinates 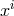 to the point with
to the point with 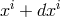 :
:
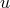 an arbitrary parameter. In the approach to Finsler geometry by Cartan [74], the starting point is the line
element:296
with
an arbitrary parameter. In the approach to Finsler geometry by Cartan [74], the starting point is the line
element:296
with 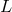 a homogeneous function of the velocity
a homogeneous function of the velocity 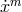 , and the Finsler metric defined by:
Quantities
, and the Finsler metric defined by:
Quantities 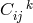 and
and 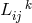 acting as connections are introduced through the change a tangent 4-vector
acting as connections are introduced through the change a tangent 4-vector
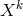 is experiencing:
where the totally symmetric object
transforms like a tensor. The asymmetric affine connection is defined by
with
is experiencing:
where the totally symmetric object
transforms like a tensor. The asymmetric affine connection is defined by
with 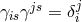 . The “geodesic coefficient”
. The “geodesic coefficient” ![2 2 2 Gp = 14γpr[∂∂˙xr(L∂x)sx˙s − ∂(∂Lxr)]](article3050x.gif) is resulting
from the Euler–Lagrange equation
is resulting
from the Euler–Lagrange equation 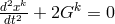 for
for 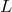 reformulated with the Finsler
metric.297
Equation (555*) can also be written as
with Cartan’s connection
reformulated with the Finsler
metric.297
Equation (555*) can also be written as
with Cartan’s connection 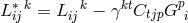 .
.
Edith Schaffhauser-Graf at the University of Fribourg in Switzerland hoped that the various curvature and torsion tensors of Cartan’s theory of Finsler spaces would offer enough geometrical structure such as to permit the building of a theory unifying electromagnetism and gravitation. She first introduced the object met before , also known as “Cartan” torsion:
and, by contraction with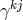 , the “torsion” vector
, the “torsion” vector 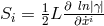 . With its help and its covariant
derivative taken to be:
the electromagnetic field tensor is defined
by:298
The form of the covariant derivative (560*) follows from the supplementary demand that the Finsler spaces
considered do allow an absolute parallelism of the line elements. Schaffhauser-Graf used the
curvature tensor 0. Varga had introduced in a “Finsler space with absolute parallelism of line
elements” ([669], Eq. (37)), excluding terms from torsion. The main physical results of her
approach are that a charged particle follows a “geodesic”, i.e., a worldline the tangent vectors
of which are parallel. The charge experiences the Lorentz force, yet this force, locally, can be
transformed away like an inertial force. Also, charge conservation is guaranteed. For vanishing
electromagnetic field, Einstein’s gravitational theory follows. It seems to me that the prize paid, i.e.,
the introduction of Finsler geometry with its numerous geometric objects, was exorbitantly
high.
. With its help and its covariant
derivative taken to be:
the electromagnetic field tensor is defined
by:298
The form of the covariant derivative (560*) follows from the supplementary demand that the Finsler spaces
considered do allow an absolute parallelism of the line elements. Schaffhauser-Graf used the
curvature tensor 0. Varga had introduced in a “Finsler space with absolute parallelism of line
elements” ([669], Eq. (37)), excluding terms from torsion. The main physical results of her
approach are that a charged particle follows a “geodesic”, i.e., a worldline the tangent vectors
of which are parallel. The charge experiences the Lorentz force, yet this force, locally, can be
transformed away like an inertial force. Also, charge conservation is guaranteed. For vanishing
electromagnetic field, Einstein’s gravitational theory follows. It seems to me that the prize paid, i.e.,
the introduction of Finsler geometry with its numerous geometric objects, was exorbitantly
high.
Stephenson’s paper on equations of motion [590*], from which the quotation above is taken,
was discussed at length by V. Hlavatý in Mathematical Reviews [ MR0098611] reproduced
below:
MR0098611] reproduced
below:
|
The paper consists of three parts. In the first part, the author points out the difference between Einstein–Maxwell field equations of general relativity and Einstein’s latest unified field equations. The first set yields the equations of motion in the form 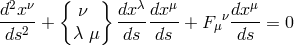 ( In the second part, the author discusses the attempt to describe unified field theory by means of a Finsler metric 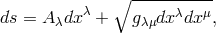 which leads by means of Remarks of the reviewer: 1) If 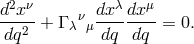 There is such a coordinate system for which the first approximation of (2) is the classical Newton gravitational law and the second approximation acquires the form (1). […]. |
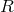 from (557*) and (551*), and to use it then
as a Lagrangian for the field equations, because he saw no possibility to arrive at a term
from (557*) and (551*), and to use it then
as a Lagrangian for the field equations, because he saw no possibility to arrive at a term 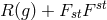 functioning as a Finslerian Lagrangian. His negative conclusion was: “It so seems that this particular
generalization of Riemannian geometry is not able to lead to a correct implementation of the electromagnetic
field.”299
functioning as a Finslerian Lagrangian. His negative conclusion was: “It so seems that this particular
generalization of Riemannian geometry is not able to lead to a correct implementation of the electromagnetic
field.”299


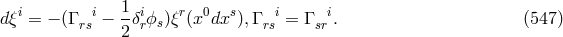
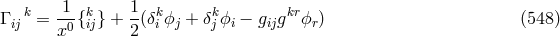
![i 1 0 i 0 i 0 i 0 m 0 i 0 m − K+ jkl = --0-2[∂k(x Γ lj ) − ∂l(x Γ kj ) + x Γ km x Γlj − x Γ lm x Γkj ] (549 ) (x )](article3021x.gif)
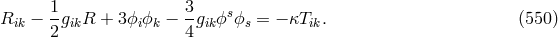

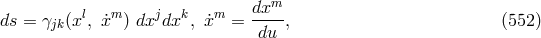


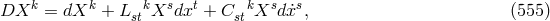
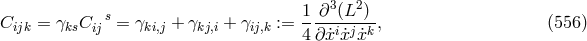
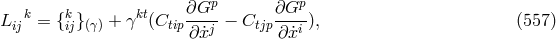

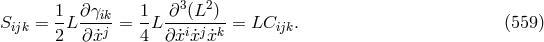
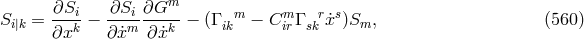

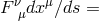 Lorentz’ force vector). Callaway’s application of the EIH method to the
second set does not yield any Lorentz force and therefore the motion of a charged particle
and of an uncharged particle would be the same.
Lorentz’ force vector). Callaway’s application of the EIH method to the
second set does not yield any Lorentz force and therefore the motion of a charged particle
and of an uncharged particle would be the same.
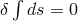 to (1) with
to (1) with ![Fμλ = 2∂[λA μ]](article3069x.gif) . However the tensor
. However the tensor
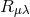 does not yield any appropriate scalar term which could be taken as Lagrangian.
[…]
does not yield any appropriate scalar term which could be taken as Lagrangian.
[…]
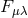 is of the second or third class (which is always the
case in Callaway’s approximation) we could have
is of the second or third class (which is always the
case in Callaway’s approximation) we could have 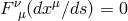 in (1) for
in (1) for 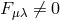 .
2) The clue to Callaway’s result is that four Einstein’s equations
.
2) The clue to Callaway’s result is that four Einstein’s equations 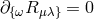 do
not contribute anything to the equations of motion of the considered singularities. If
one replaces these four differential equations of the third order by another set of four
differential equations of the third order, then the kinematical description of the motion
results in the form
do
not contribute anything to the equations of motion of the considered singularities. If
one replaces these four differential equations of the third order by another set of four
differential equations of the third order, then the kinematical description of the motion
results in the form