Next: 5. A bijection between
Up: Schröder Triangles, Paths, and
Previous: 3. Zebras, generating trees
4. New constructions for zebras
Using the background of the previous sections we
introduce two new zebra constructions. We then consider
the enumeration
of certain subsets of zebras by
the recurrence relations
(1) and
(4). Comparing Table
4 with Table 1 indicates the
relationships of these constructions to (1) and to
(4).
4.1 The construction CONSTRC
We describe an inductive construction for zebras that essentially adds rows with
color change (see Figure 2).
Figure 2:
The construction of zebras related to
CONSTRC.
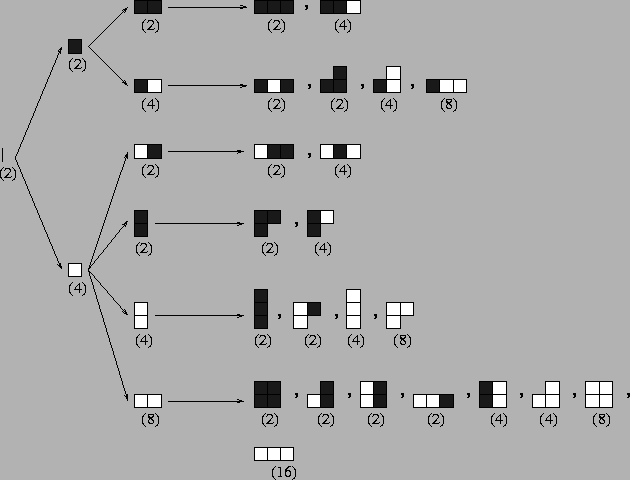 |
This construction begins with Z1 = {|}. Assuming
that Zn, 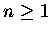 ,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra
P in Zn,
either
,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra
P in Zn,
either
-
by appending a white or black cell to the right of the top row of P, or
-
by forming a new right justified row with any arrangement of colors above
the rightmost consecutive white cells of the top row of P. The underlying
columns receive the color of each new top cell.
Proposition 4.1
The construction
CONSTRC produces all zebras uniquely and
satisfies the succession rules
given in the upper-right cell of Table
3.
Denote the number of rightmost consecutive white cells on the top
row of a zebra P by ur(P).
Define Zn,k to be the subset of zebras, P, for which n(P) = nand
ur(P) = k.
Proof of Prop. 4.1.
For  it is straight forward to check that each zebra in
Zn+1 has a unique parent in Zn and thus by induction
each zebra will be constructed exactly once. Establishing the
rules requires some attention.
Given the construction, we observe that
it is straight forward to check that each zebra in
Zn+1 has a unique parent in Zn and thus by induction
each zebra will be constructed exactly once. Establishing the
rules requires some attention.
Given the construction, we observe that
- 1.
- For
 , each P in Zn,k is the parent of
2k-j zebras in
Zn+1, j.
We prove this in three cases:
, each P in Zn,k is the parent of
2k-j zebras in
Zn+1, j.
We prove this in three cases:
- (a)
- For 0 = j = k, P' in
Zn+1, j results when a B is appended to the right of the top row of P.
- (b)
- For 0 = j < k, a P' in
Zn+1, j results either when a B is appended to the right of the top row of P or when an arbitrary row of length i, for
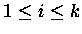 ,
ending in B forms the new top row. There are
,
ending in B forms the new top row. There are
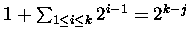 ways to do so.
ways to do so.
- (c)
- If
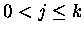 ,
then P' in
Zn+1, j results either when
a string of j W's
forms the new top row or when a row of length i , for
,
then P' in
Zn+1, j results either when
a string of j W's
forms the new top row or when a row of length i , for
 ,
ending in B followed by j W's forms the new top row. There are
,
ending in B followed by j W's forms the new top row. There are
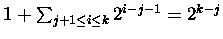 choices.
choices.
- 2.
- For
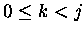 , each P in Zn,k has only one
child in P' in
Zn+1, k+1 and none in
Zn+1, j for j>k+1.
The sole child results from appending a W to the right of the top row of P.
, each P in Zn,k has only one
child in P' in
Zn+1, k+1 and none in
Zn+1, j for j>k+1.
The sole child results from appending a W to the right of the top row of P.
- 3.
- For
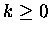 , each P in Zn, k is the parent of
2k+1 zebras is Zn+1, and conversely.
The first clause is obtained by summing the results of 1. and 2. The converse
follows the matching of k with 2k+1.
, each P in Zn, k is the parent of
2k+1 zebras is Zn+1, and conversely.
The first clause is obtained by summing the results of 1. and 2. The converse
follows the matching of k with 2k+1.
Using these three observations we establish the rules. If P has 2kchildren, then P belongs to Zn,k+1. For
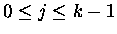 ,
P is the parent of 2k-j-1 zebras in Zn+1,j. Each of these is
the parent of
2 j + 1 zebras in Zn+2.
Finally, each P in
Zn, k-1 has one child in Zn+1,k,
which in turn has 2k+1 children.
,
P is the parent of 2k-j-1 zebras in Zn+1,j. Each of these is
the parent of
2 j + 1 zebras in Zn+2.
Finally, each P in
Zn, k-1 has one child in Zn+1,k,
which in turn has 2k+1 children.

The following proposition shows that
|Zn,k| appears on the kth diagonal above the principal
diagonal in the Schröder triangle of Table
1a.
In Section 5 we prove this proposition
in a bijective manner
consistent with the above construction. In Section 6.2
we prove it while linking CONSTRA to
CONSTRC.
Proposition 4.2
When
S(
m,
n) denotes
|
Zn+1, n-m|,
S(
m,
n) satisfies the recurrence (
1).
Table 4:
The frequencies of the labels for two generating trees of Section
4.
|
4.2 The construction CONSTRD
Next we describe a construction for zebras
that essentially adds columns with
color change. This construction agrees with the
recurrence (4).
While it is absent in
[2], the corresponding succession rule does appear in
of Lemma 4.3 of [2].
This inductive construction begins with Z1 = {|}. Assuming
that Zn, 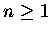 ,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra P in Zn,
either
,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra P in Zn,
either
-
by placing
a new cell of either color on top of the rightmost column when that
column is white, so that the new column receives the color of the top cell, or
- by first
attaching a new top justified white or black column of any length
to the right side of
P and then interchanging the colors of the new column with the
rightmost column of P when their colors differ.
Let Zn,c|k be the set of zebras in Zn,
each having exactly k cells of color c in its rightmost column.
Let
Zn,d|j,c|k be the set of zebras in Zn,c|k,
each having at least two cells on its top row and having
exactly j cells of color d in the next to the rightmost
column.
When we restrict our attention to those zebras having a white right column,
then the CONSTRD corresponds to the triangle for R(m,n);
hence, with appropriate indexing
|Zn,W|k|, for k>0, appears in the Schröder triangle of Table
1b. More
precisely, we have
Proposition 4.3
For
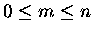
,
suppose
R(
m,
n) denotes
|
Zn+2,W|n+1-m|,
the number of zebras in
Zn+2, each
having
n+1-
m white cells in its rightmost column.
R(
m,
n)
satisfies the recurrence (
4).
Proof.
For k>0,
Thus
and the result follows after an appropriate change of indices.

We remark that this proof can be modified into
a bijective proof involving lattice paths
similar to the result in Section 5.
In a manner comparable to the proof of Proposition 4.1, one can
show
Proposition 4.4
The construction
CONSTRD produces all zebras and
satisfies the succession rules
given in the lower-right cell of Table
3.
Notably zebras afford us bijective proofs that relate the row sums of each
Schröder triangle to
the diagonal entries of the other, as is now seen.
Proof.
Observe that
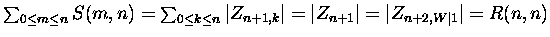 .
To prove the second identity, observe that
.
To prove the second identity, observe that

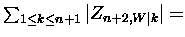
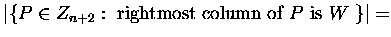
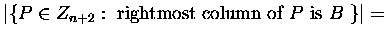 | Zn+2,0| =
S(n+1,n+1).
| Zn+2,0| =
S(n+1,n+1).

Next: 5. A bijection between
Up: Schröder Triangles, Paths, and
Previous: 3. Zebras, generating trees

![]() it is straight forward to check that each zebra in
Zn+1 has a unique parent in Zn and thus by induction
each zebra will be constructed exactly once. Establishing the
rules requires some attention.
Given the construction, we observe that
it is straight forward to check that each zebra in
Zn+1 has a unique parent in Zn and thus by induction
each zebra will be constructed exactly once. Establishing the
rules requires some attention.
Given the construction, we observe that
![]() ,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra P in Zn,
either
,
has been constructed, we construct all
possible
zebras of semiperimeter n+1, obtaining each from some zebra P in Zn,
either
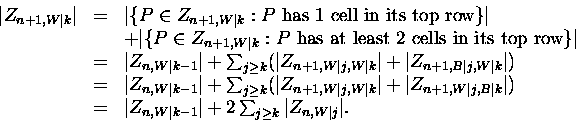
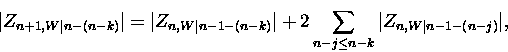
![]() .
To prove the second identity, observe that
.
To prove the second identity, observe that
![]()
![]()
![]()
![]() | Zn+2,0| =
S(n+1,n+1).
| Zn+2,0| =
S(n+1,n+1).
![]()