Up: Schröder Triangles, Paths, and
Previous: 7. An algorithm for
- 1
-
E. Barcucci, S. Lanini, A. Del Lungo, M. Macri, R. Pinzani, The inversion number of some permutations with forbidden subsequences, Proc. of the International Symposium on Combinatorics and Applications Tianjin (China) (1996).
- 2
-
E. Barcucci, A. Del Lungo, S. Fezzi and R. Pinzani, Some combinatorial interpretations of q-analogues of Schröder numbers, COMBINATORICS'96, Assisi (Italy) (1996).
- 3
-
J. Bonin, L. Shapiro, R. Simion, Some q-analogues of the Schröder numbers arising from combinatorial statistics on lattice paths, J. Statistical Planning and Inference 34 (1993) 35-55.
- 4
-
A. Cayley, On the analytical form called trees, Part II, Philos. Mag. (4) 18 (1859), 374-378.
- 5
-
F. R. K. Chung, R. L. Graham, V. E. Hoggatt Jr, M. Kleiman, The number of Baxter permutations, J. Combinatorial Theory (Series A), 24 (1978), 382-394.
- 6
- A. Erdélyi and I. M. H. Etherington,
Some problems of non-associative combinatorics (2), Edinburgh Math.
Notes 32 (1940), 7-12.
- 7
-
I. M. H. Etherington,
Some problems of non-associative combinatorics (1), Edinburgh Math.
Notes 32 (1940), 1-6.
- 8
-
D. Foata, D. Zeilberger, A classic proof of a recurrence for
a very classical sequence, J. Comb. Theor.-Ser. A., 80 (1997),
380-384.
- 9
-
S. Gire, Arbres, permutations à motifs exclus et cartes planaires: quelques problèmes algorithmiques et combinatoires, Thèse de l'Université de Bordeaux I (1993).
- 10
-
O. Guibert, Combinatoire des permutations à motifs exclus en liaison avec mots, cartes planaires et tableaux de Young, Thèse de l'Université de Bordeaux I (1995).
- 11
- L. Habsieger, M. Kazarian, and S. Lando,
On the second number of Plutarch,
Am. Math. Monthly,
105 (1998) 446.
- 12
-
J.
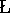 ukasiewicz, Selected Works (L. Borkowski, ed.), North-Holland, Amsterdam (1970).
ukasiewicz, Selected Works (L. Borkowski, ed.), North-Holland, Amsterdam (1970).
- 13
-
Plutarch, Moralia, Vol. IX, Loeb Classical Library, Harvard
Univ. Press, Cambridge, Mass., 1961
- 14
-
G. N. Raney, Functional composition patterns and power series reversion,
Trans. Amer. Math. Soc. 94 (1960), 441-451.
- 15
-
D. G. Rogers and L. W. Shapiro, Deques, trees and lattice paths,
Combinatorial Mathematics VIII: Proceedings of the Eighth Australian
Conference. Lecture Notes in Mathematics, vol 882, Springer-Verlag,
Berlin (1981) 293-303.
- 16
-
D. G. Rogers,
The enumeration of a family of ladder
graphs part II: Schröder and superconnective relations,
Quart. J. Math. Oxford (2) 31 (1980) 491-506.
- 17
-
D. G. Rogers,
Pascal triangles, Catalan numbers and renewal arrays,
Discrete Math 22 (1978) 301-310.
- 18
-
D. G. Rogers,
A Schröder triangle,
Combinatorial Mathematics V: Proceedings of the Fifth Australian
Conference. Lecture Notes in Mathematics, vol 622, Springer-Verlag,
Berlin (1977) 175-196.
- 19
-
D. G. Rogers, L. W. Shapiro, Some correspondence involving the Schröder numbers and relations, Comb. Math., Proc. of the intern. Conf., Camberra 1977, Lecture Notes in Math. 686, Springer Verlag (1978), 267-276.
- 20
- E. Schröder, Vier Kombinatorische Probleme,
Z. Math. Phys. 15 (1870) 361-376.
- 21
-
L. W. Shapiro, S. Geta, W-J. Woan, and L. Woodson, The Riordan Group,
Discrete Appl. Math. 34 (1991) 229-239.
- 22
- N. J. A. Sloane,
On-Line Encyclopedia of Integer Sequences,
http://oeis.org.
- 23
-
R. Sprugnoli and C. Verri, Catalan, Motzkin and Schröder walks, report RT 8/91, Dipartimento di Sistemi e Informatica, Università di Firenze (1991).
- 24
-
R. P. Stanley, Hipparchus, Plutarch, Schröder and Hough, Amer. Math. Monthly, 104 (1997) 344-350.
- 25
-
R. A. Sulanke, A recurrence restricted by a diagonal condition: generalized Catalan array, Fibonacci Q., 27 (1989), 33-46.
- 26
-
R. A. Sulanke, Bijective recurrences concerning Schroder paths,
preprint 1998.
- 27
- R. A. Sulanke, Three recurrences
for parallelogram polyominoes, 1997, to appear in J. of
Difference Eq. and Appl.
- 28
-
J. West, Generating trees and the Catalan and Schröder numbers, Discrete Mathematics 146 (1995), 247-262.