6.1 A brief review of results for recurrence arrays
For orientation and reference we review
some known techniques for dealing with arbitrary recurrence
arrays. For any real sequence
![]() ,
with
,
with
![]() ,
consider the two arrays,
,
consider the two arrays,
![]() and
and
![]() that, for
that, for
![]() ,
satisfy the recurrence
,
satisfy the recurrence
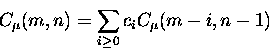
As an example, one can
obtain, for
![]() ,
,
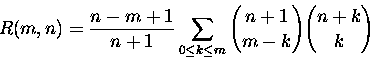
6.2 Enumerating Zn by the number rightmost top white cells
In this section we again consider the cardinalities
![]() ,
where
,
where
![]() and
and ![]() .
We first compute the generating function
.
We first compute the generating function
![]() for
for ![]() .
We then determine the coefficients in
Corollary 6.3.
It seems interesting how CONSTRA is used in modified form
in the following proof.
.
We then determine the coefficients in
Corollary 6.3.
It seems interesting how CONSTRA is used in modified form
in the following proof.
Proof.
For ![]() ,
let
,
let
![]() denote
the zebra consisting of a single row of white cells of length j and let
denote
the zebra consisting of a single row of white cells of length j and let
![]() .
Modify
the construction CONSTRA
by reversing its ``direction'' from up-and-to-the-right
to proceed down-and-to-the-left and by starting the construction with
the zebra
.
Modify
the construction CONSTRA
by reversing its ``direction'' from up-and-to-the-right
to proceed down-and-to-the-left and by starting the construction with
the zebra
![]() .
Now we construct the zebras inductively
either
by adding left justified rows to the bottom of the zebras where each new
cell is colored as the above column or by adding a new cell of either color
to the left of the lowest row (see Figure 4).
For
.
Now we construct the zebras inductively
either
by adding left justified rows to the bottom of the zebras where each new
cell is colored as the above column or by adding a new cell of either color
to the left of the lowest row (see Figure 4).
For ![]() such that ur(P) = j, let T(P)denote the set of the children of P in Zn+1 under
the modified construction. We can recursively decompose
A(j) into a union of disjoint sets.
This decomposition illustrated is in
Figure 5
for the case j=3 and
an arbitrary zebra P in
A(j).
such that ur(P) = j, let T(P)denote the set of the children of P in Zn+1 under
the modified construction. We can recursively decompose
A(j) into a union of disjoint sets.
This decomposition illustrated is in
Figure 5
for the case j=3 and
an arbitrary zebra P in
A(j).
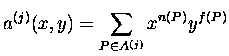 where f(P)= the length of the lowest row of P. The decomposition
of (8) translates
to the following equation.
where f(P)= the length of the lowest row of P. The decomposition
of (8) translates
to the following equation.
To obtain the above one can easily check that the telescoping
sum
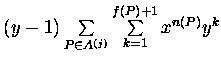 is equal to
y2a(j)(x,y)-ya(j)(x,1).
Equation (9) implies
is equal to
y2a(j)(x,y)-ya(j)(x,1).
Equation (9) implies
Proof.
Equation (7) implies
The bijection between paths and zebras and this corollary yield, for
![]() ,
,
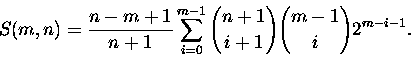
6.3 Enumerating Zn by the length of the rightmost column
Here we consider again the numbers
![]() ,
where rc(P) denotes the number
of white cells in the right column of P. Since this section is similar to
the previous section, the treatment is brief.
,
where rc(P) denotes the number
of white cells in the right column of P. Since this section is similar to
the previous section, the treatment is brief.
Proof.
It will be interesting how CONSTRB
is used.
Let
![]() where W|j is a white column of
length j.
We modify
CONSTRB
by reversing its ``direction'' from up-and-to-the-right
to proceed down-and-to-the-left.
Starting from the zebra W|j, we
then construct inductively all zebras in B|j by
adding bottom justified columns of either color on the left or
by adding a new cell to the bottom of the leftmost column so that
the cell retains the color of the column above.
For
where W|j is a white column of
length j.
We modify
CONSTRB
by reversing its ``direction'' from up-and-to-the-right
to proceed down-and-to-the-left.
Starting from the zebra W|j, we
then construct inductively all zebras in B|j by
adding bottom justified columns of either color on the left or
by adding a new cell to the bottom of the leftmost column so that
the cell retains the color of the column above.
For ![]() such that rc(P) = j, let T'(P) denote
the set of the children of P in Zn+1.
We can recursively decompose B|j
into a union of
disjoint sets as follows:
such that rc(P) = j, let T'(P) denote
the set of the children of P in Zn+1.
We can recursively decompose B|j
into a union of
disjoint sets as follows:
With
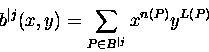
which implies