Next: 6. Generating function considerations Up: Schröder Triangles, Paths, and Previous: 4. New constructions for

  
5. A bijection between zebras and lattice paths

Here we establish a bijection between lattice paths in S[x,y], defined in Section 2, and the zebras in Zn+1,n-m. Since the bijection is consistent with the recurrence (1), its existence establishes Proposition 4.2. Notice that for a lattice path the difference n-m is the horizontal distance from the terminus to the constraint y=x, while the difference n-m represents fertility of a zebra.

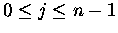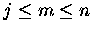The inductively defined bijection begins by matching the trivial polyomino | with the point path. Suppose that, for some $0\leq j \leq n-1$, the sets S[j,n-1] and Zn,n-j-1 have been matched. To show how S[m,n] and Zn+1,n-m can be matched, consider the step from (j,n-1) to (m,n) for $j \leq m \leq n$. There are three cases:

1.
When m = j, the step has weight 1 and 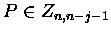$P \in Z_{n,n-j-1}$ produces only one zebra in Zn+1,n-m that is obtained by appending a W cell to the right of top row of P. See Figure 3 (a).
2.
When j < m<n, the last step of the path has weight, or multiplicity, 2m-j-1. (We record the following scheme in Table 5 for the case m-j = 3 and n-m = 2.) We list the first 2m-j-1 nonnegative integers in binary form without unnecessary leading zeros. We replace the first integer in this list, which is 0, by a blank. For all other integers in this list, we replace each 1 by B and each remaining 0 by a W. We then reverse each pattern, right justify each pattern, and append n-m W's to each result. The resulting patterns are the top rows for the set of the 2m-j-1 zebras in Zn+1,n-m corresponding to the path in S(m,n). See Figure 3(b,c).
3.
When j < m = n, we can use the scheme of the second case by modifying the subcase of ``blank'' to simply appending a B to the right of the top row of P.
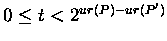In the second and third cases the underlying columns take the colors of the added cells. In Figure 3 ``t'' is an integer satisfying $0\leq t 2^{ur(P)-ur(P')}$. \fbox{}


  
Table 5: The encodings for the new top rows.
\begin{table} \begin{displaymath} \begin{array}{\vert c\vert c\vert r\vert} \hli... ...d \\ 11 & BB & B B WW \quad \\ \hline \end{array}\end{displaymath}\end{table}



  
Figure: The path to zebra bijection for $1 \leq m \leq n$.
\begin{figure} \begin{center} \mbox{\psfig{file=FIGSWEB/fig3.ps,width=12cm} }\end{center}\end{figure}


Next: 6. Generating function considerations Up: Schröder Triangles, Paths, and Previous: 4. New constructions for