Next: 4. New constructions for Up: Schröder Triangles, Paths, and Previous: 2. Schröder arrays and

   
3. Zebras, generating trees and previous constructions

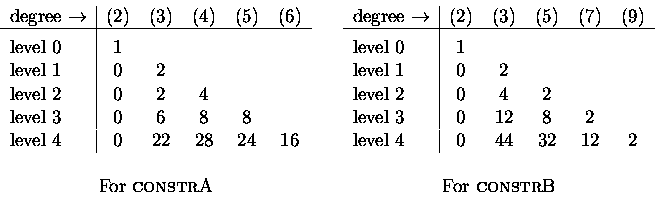
A parallelogram polyomino is a translation invariant array of unit squares bounded by two lattice paths that use the steps (0,1) and (1,0), and intersect only initially and finally. The semiperimeter of a polyomino is the length of either of these paths; the width of a polyomino is the number of its columns. We will consider parallelogram polyominoes consisting of black and white columns, called zebras. Barcucci, Del Lungo, Fezzi, and Pinzani [2] showed that R(n-1,n-1) counts the set of zebras with semiperimeter n. In the following we denote the cardinality of any set A by |A|. We denote the set of all zebras by Z, the semiperimeter of a zebra P by n(P), and the set {P in Z : n(P) = n} by Z_n. It is convenient to take the trivial zebra to be the vertical unit segment denoted by |; hence, Z₁ = {|}.

Before proceeding we recall from [5] the definition of a generating tree for a set of succession rules: A generating tree is a rooted, labeled tree in which the labels of the set of children of each node x are determined solely from the label of x. Thus any particular generating tree can be specified by a set of succession rules, i.e., a recursive definition, consisting of

1.

(the basis) the label of the root,

2.

(the inductive step) a set of succession rules that yields a multiset of labeled children each of which depends solely on the label of the parent.

The next two subsections record the generating trees of two constructions for zebras introduced by Barcucci et al.[2]. They focused on succession rules (or, rewriting rules) principally to study permutations with forbidden subsequences. Upon tabulating the frequency distributions for the out-degrees of the vertices at each level in the generating trees for the rules associated with the zebra constructions that follow, one can obtain arrays that contain the Schröder numbers, as in Table 2.

 

Table 2: The frequencies of the labels for two generating trees of Section 3.

$$\begin{array}{cc} \begin{array}{c} \begin{tabular}{l\vert ccc... ...bular}\\ \ \\ \mbox{For {\sc constr}B} \end{array}\end{array}$$

 

3.1 The construction CONSTRA

Theorem 7.3 of [2] gives the following inductive construction for the set of all zebras. Beginning with Z₁ = {|}, and assuming that Z_n, $n \geq 1$, has been constructed, one constructs all possible zebras of semiperimeter n+1, each obtained from some zebra P in Z_n, either

• by appending a new white or black cell to the right of the top row of P, or
• by forming a new right-justified row of any length above the top row of P. The new cells receive the colors of the underlying columns.

This construction essentially grows zebras by adding rows and without changing the colors to the underlying parent zebra. Its generating tree is illustrated in Figure 1 and the corresponding succession rules appear in Table 3. Notice the appearances of the Schröder numbers, both in the second column and as row sums, in Table 2 that gives the frequencies for the outdegrees of the vertices of the generating tree for this construction.

  

Figure 1: The generating tree related to CONSTRA

 

Table 3: Zebra construction schemes and succession rules.

Scheme	without color change	with color change
$\begin{array}{lll} \ \\ \textrm{essentially} \\ \textrm{adding}\\ \textrm{rows} \end{array}$	$\begin{array}{l} \textsc{constr}\textrm{A}:\\ (2) \rightarrow (3)(3)\\ (k) \rightarrow (3)\cdots(k) (k+1)^2 \end{array}$	$\begin{array}{l} \textsc{constr}\textrm{C}:\\ (2) \rightarrow (2)(4)\\ (2^k) \rightarrow (2)^{2^{k-1}}\cdots(2^{k-1})^2 (2^k)(2^{k+1}) \end{array}$
$\begin{array}{lll} \ \\ \textrm{essentially} \\ \textrm{adding}\\ \textrm{columns} \end{array}$	$\begin{array}{l} \textsc{constr}\textrm{B}:\\ (2) \rightarrow (3)(3)\\ (2k-1) \rightarrow (3)^{2}\cdots(2k-1)^2 (2k+1) \end{array}$	$\begin{array}{l} \textsc{constr}\textrm{D}:\\ (2) \rightarrow (2)(4)\\ (2k) \rightarrow (2)(4)^2\cdots(2k)^2 (k+1) \end{array}$

3.2 The construction CONSTRB

Theorem 5.2 of [2] gives a second construction for the set of all zebras. The construction begins with $Z_1 = \{\vert\}$. Assuming that Z_n, $n \geq 1$, has been constructed, one constructs Z_n+1 to be the set of all possible zebras of semiperimeter n+1, each obtained from some parent zebra P in Z_n, either

• by placing a cell above the rightmost column of P so the new cell receives the color of the underlying column, or
• by attaching a new top justified white or black column of any length to the right side of P (of course, without increasing the number of rows).

This construction essentially grows zebras by adding columns and without changing the color of the underlying parent zebra. The corresponding succession rules appear in Table 3. See also Table 2.

Next: 4. New constructions for Up: Schröder Triangles, Paths, and Previous: 2. Schröder arrays and