Notation and conventions
Unless otherwise and explicitly stated, we use geometrized units where
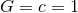
, so that energy and
time have units of length. Geometric objects are denoted with boldface symbols, whereas their components
are not. We also adopt the
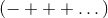
convention for the metric. For reference, the following is a list of
symbols that are used often throughout the text.
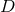 |
Total number of spacetime dimensions (we always consider one timelike |
| |
and  spacelike dimensions). spacelike dimensions). |
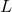 |
Curvature radius of (A)dS spacetime, related to the (negative) positive |
| |
cosmological constant 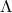 in the Einstein equations ( in the Einstein equations (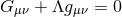 ) ) |
| |
through 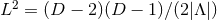 . . |
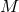 |
BH mass. |
 |
BH rotation parameter. |
 |
Radius of the BH’s event horizon in the chosen coordinates. |
 |
Fourier transform variable. The time dependence of any field is 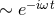 . . |
| |
For stable spacetimes,  . . |
 |
Spin of the field. |
 |
Integer angular number, related to the eigenvalue 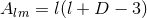 |
| |
of scalar spherical harmonics in 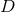 dimensions. dimensions. |
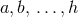 |
Index range referred to as “early lower case Latin indices” |
| |
(likewise for upper case indices). |
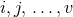 |
Index range referred to as “late lower case Latin indices” |
| |
(likewise for upper case indices). |
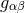 |
Spacetime metric; greek indices run from 0 to  . . |
 |
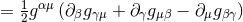 , Christoffel symbol associated with the , Christoffel symbol associated with the |
| |
spacetime metric 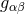 . . |
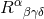 |
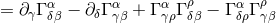 , Riemann curvature tensor of the , Riemann curvature tensor of the |
| |
 -dimensional spacetime. -dimensional spacetime. |
 |
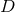 -dimensional covariant derivative associated with -dimensional covariant derivative associated with 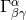 . . |
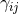 |
Induced metric, also known as first fundamental form, on |
| |
 -dimensional spatial hypersurface; latin indices run from 1 to -dimensional spatial hypersurface; latin indices run from 1 to  . . |
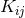 |
Extrinsic curvature, also known as second fundamental form, on |
| |
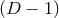 -dimensional spatial hypersurface. -dimensional spatial hypersurface. |
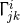 |
 -dimensional Christoffel symbol associated with -dimensional Christoffel symbol associated with 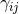 . . |
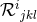 |
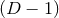 -dimensional Riemann curvature tensor of the spatial hypersurface. -dimensional Riemann curvature tensor of the spatial hypersurface. |
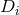 |
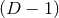 -dimensional covariant derivative associated with -dimensional covariant derivative associated with 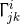 . . |
 |
 -dimensional sphere. -dimensional sphere. |
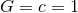 , so that energy and
time have units of length. Geometric objects are denoted with boldface symbols, whereas their components
are not. We also adopt the
, so that energy and
time have units of length. Geometric objects are denoted with boldface symbols, whereas their components
are not. We also adopt the 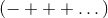 convention for the metric. For reference, the following is a list of
symbols that are used often throughout the text.
convention for the metric. For reference, the following is a list of
symbols that are used often throughout the text.
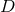
 spacelike dimensions).
spacelike dimensions). 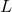
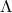 in the Einstein equations (
in the Einstein equations (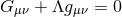 )
) 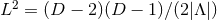 .
. 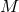



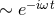 .
.  .
. 

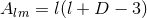
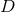 dimensions.
dimensions. 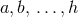
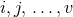
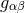
 .
. 
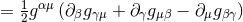 , Christoffel symbol associated with the
, Christoffel symbol associated with the 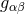 .
. 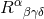
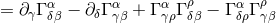 , Riemann curvature tensor of the
, Riemann curvature tensor of the  -dimensional spacetime.
-dimensional spacetime. 
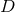 -dimensional covariant derivative associated with
-dimensional covariant derivative associated with 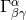 .
. 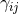
 -dimensional spatial hypersurface; latin indices run from 1 to
-dimensional spatial hypersurface; latin indices run from 1 to  .
.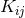
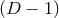 -dimensional spatial hypersurface.
-dimensional spatial hypersurface. 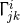
 -dimensional Christoffel symbol associated with
-dimensional Christoffel symbol associated with 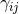 .
. 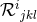
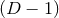 -dimensional Riemann curvature tensor of the spatial hypersurface.
-dimensional Riemann curvature tensor of the spatial hypersurface. 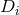
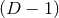 -dimensional covariant derivative associated with
-dimensional covariant derivative associated with 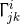 .
. 
 -dimensional sphere.
-dimensional sphere.