4 The CMB and Cosmological Estimates of the Distance Scale
4.1 The physics of the anisotropy spectrum and its implications
The physics of stellar distance calibrators is very complicated, because it comes from the era in
which the Universe has had time to evolve complicated astrophysics. A large class of alternative
approaches to cosmological parameters in general involve going back to an era where astrophysics is
relatively simple and linear, the epoch of recombination at which the CMB fluctuations can be
studied. Although tests involving the CMB do not directly determine 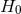 , they provide joint
information about
, they provide joint
information about 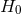 and other cosmological parameters which is improving at a very rapid
rate.
and other cosmological parameters which is improving at a very rapid
rate.
In the Universe’s early history, its temperature was high enough to prohibit the formation of atoms, and
the Universe was therefore ionized. Approximately 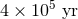 after the Big Bang, corresponding to
a redshift
after the Big Bang, corresponding to
a redshift 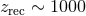 , the temperature dropped enough to allow the formation of atoms,
a point known as “recombination”. For photons, the consequence of recombination was that
photons no longer scattered from ionized particles but were free to stream. After recombination,
these primordial photons reddened with the expansion of the Universe, forming the cosmic
microwave background (CMB) which we observe today as a black-body radiation background at
2.73 K.
, the temperature dropped enough to allow the formation of atoms,
a point known as “recombination”. For photons, the consequence of recombination was that
photons no longer scattered from ionized particles but were free to stream. After recombination,
these primordial photons reddened with the expansion of the Universe, forming the cosmic
microwave background (CMB) which we observe today as a black-body radiation background at
2.73 K.
In the early Universe, structure existed in the form of small density fluctuations (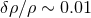 ) in the
photon-baryon fluid. The resulting pressure gradients, together with gravitational restoring forces, drove
oscillations, very similar to the acoustic oscillations commonly known as sound waves. Fluctuations prior
to recombination could propagate at the relativistic (
) in the
photon-baryon fluid. The resulting pressure gradients, together with gravitational restoring forces, drove
oscillations, very similar to the acoustic oscillations commonly known as sound waves. Fluctuations prior
to recombination could propagate at the relativistic (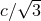 ) sound speed as the Universe
expanded. At recombination, the structure was dominated by those oscillation frequencies which had
completed a half-integral number of oscillations within the characteristic size of the Universe at
recombination;19
this pattern became frozen into the photon field which formed the CMB once the photons and
baryons decoupled and the sound speed dropped. The process is reviewed in much more detail
in [92].
) sound speed as the Universe
expanded. At recombination, the structure was dominated by those oscillation frequencies which had
completed a half-integral number of oscillations within the characteristic size of the Universe at
recombination;19
this pattern became frozen into the photon field which formed the CMB once the photons and
baryons decoupled and the sound speed dropped. The process is reviewed in much more detail
in [92].
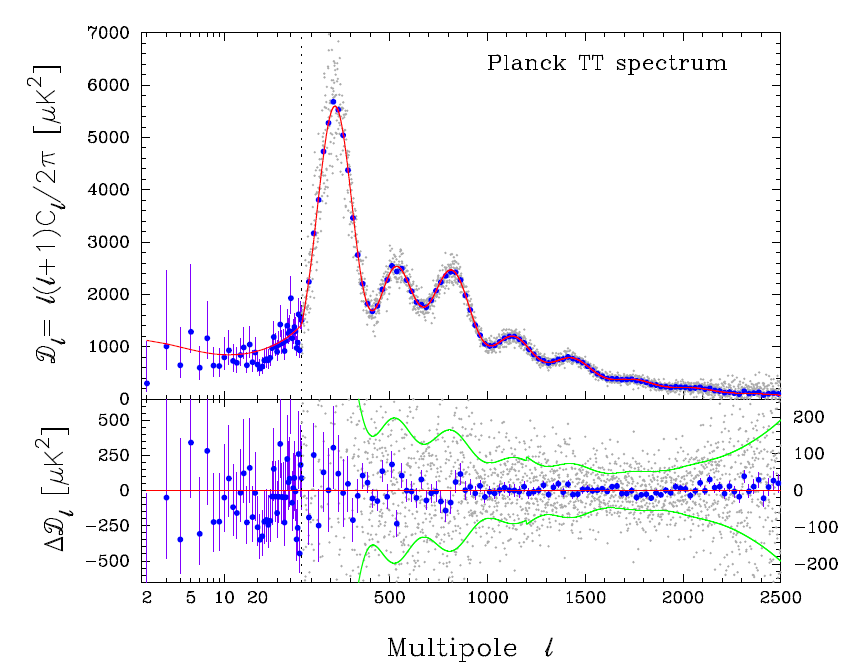
The resulting “acoustic peaks” dominate the fluctuation spectrum (see Figure 8*). Their angular scale is
a function of the size of the Universe at the time of recombination, and the angular diameter distance
between us and 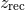 . Since the angular diameter distance is a function of cosmological parameters,
measurement of the positions of the acoustic peaks provides a constraint on cosmological parameters.
Specifically, the more closed the spatial geometry of the Universe, the smaller the angular diameter distance
for a given redshift, and the larger the characteristic scale of the acoustic peaks. The measurement of the
peak position has become a strong constraint in successive observations (in particular BOOMERanG [47],
MAXIMA [83], and WMAP, reported in [201*] and [202*]) and corresponds to an approximately spatially
flat Universe in which
. Since the angular diameter distance is a function of cosmological parameters,
measurement of the positions of the acoustic peaks provides a constraint on cosmological parameters.
Specifically, the more closed the spatial geometry of the Universe, the smaller the angular diameter distance
for a given redshift, and the larger the characteristic scale of the acoustic peaks. The measurement of the
peak position has become a strong constraint in successive observations (in particular BOOMERanG [47],
MAXIMA [83], and WMAP, reported in [201*] and [202*]) and corresponds to an approximately spatially
flat Universe in which 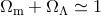 .
.
But the global geometry of the Universe is not the only property which can be deduced from the fluctuation
spectrum.20
The peaks are also sensitive to the density of baryons, of total (baryonic + dark) matter, and of vacuum
energy (energy associated with the cosmological constant). These densities scale with the square
of the Hubble parameter times the corresponding dimensionless densities [see Eq. (5*)] and
measurement of the acoustic peaks therefore provides information on the Hubble constant, degenerate
with other parameters, principally 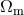 and
and 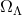 . The second peak strongly constrains the
baryon density,
. The second peak strongly constrains the
baryon density, 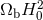 , and the third peak is sensitive to the total matter density in the form
, and the third peak is sensitive to the total matter density in the form
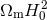 .
.
4.2 Degeneracies and implications for H0
Although the CMB observations provide significant information about cosmological parameters, the
available data constrain combinations of 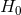 with other parameters, and either assumptions or other data
must be provided in order to derive the Hubble constant. One possible assumption is that the Universe is
exactly flat (i.e.,
with other parameters, and either assumptions or other data
must be provided in order to derive the Hubble constant. One possible assumption is that the Universe is
exactly flat (i.e., 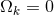 ) and the primordial fluctuations have a power law spectrum. In this case
measurements of the CMB fluctuation spectrum with the Wilkinson Anisotropy Probe (WMAP) satellite
[201, 202*] and more recently with the Planck satellite [2*], allow
) and the primordial fluctuations have a power law spectrum. In this case
measurements of the CMB fluctuation spectrum with the Wilkinson Anisotropy Probe (WMAP) satellite
[201, 202*] and more recently with the Planck satellite [2*], allow 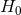 to be derived. This is because
measuring
to be derived. This is because
measuring 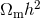 produces a locus in the
produces a locus in the 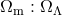 plane which is different from the
plane which is different from the 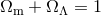 locus
of the flat Universe, and although the tilt of these two lines is not very different, an accurate CMB
measurement can localise the intersection enough to give
locus
of the flat Universe, and although the tilt of these two lines is not very different, an accurate CMB
measurement can localise the intersection enough to give 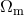 and
and 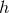 separately. The value of
separately. The value of
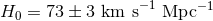 was derived in this way by WMAP [202] and, using the more
accurate spectrum provided by Planck, as
was derived in this way by WMAP [202] and, using the more
accurate spectrum provided by Planck, as 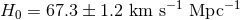 [2*]. In this case,
other cosmological parameters can be determined to two and in some cases three significant
figures,21
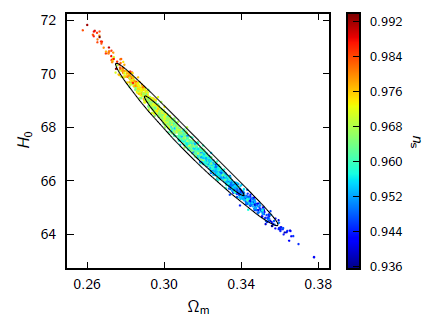
Figure 9* shows this in another way, in terms of
[2*]. In this case,
other cosmological parameters can be determined to two and in some cases three significant
figures,21
Figure 9* shows this in another way, in terms of 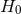 as a function of
as a function of 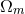 in a flat universe [
in a flat universe [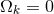 in
Eq. (10*)].
in
Eq. (10*)].
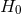 ,
, 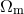 , from the 2013 Planck data, is shown as
a series of points. A flat Universe is assumed, together with information from the Planck fluctuation
temperature spectrum, CMB lensing information from Planck, and WMAP polarization observations.
The colour coding reflects different values of
, from the 2013 Planck data, is shown as
a series of points. A flat Universe is assumed, together with information from the Planck fluctuation
temperature spectrum, CMB lensing information from Planck, and WMAP polarization observations.
The colour coding reflects different values of 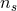 , the spectral index of scalar perturbations as a
function of spatial scale at early times. Image reproduced with permission from [2*], copyright by
ESO.
, the spectral index of scalar perturbations as a
function of spatial scale at early times. Image reproduced with permission from [2*], copyright by
ESO. If we do not assume the universe to be exactly flat, as is done in Figure 9*, then we obtain a degeneracy
with 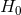 in the sense that decreasing
in the sense that decreasing 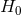 increases the total density of the universe (approximately by
0.1 in units of the critical density for a 20 km s−1 Mpc−1 decrease in
increases the total density of the universe (approximately by
0.1 in units of the critical density for a 20 km s−1 Mpc−1 decrease in 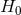 ). CMB data by themselves,
without any further assumptions or extra data, do not supply a significant constraint on
). CMB data by themselves,
without any further assumptions or extra data, do not supply a significant constraint on 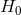 compared to
those which are obtainable by other methods. Other observing programmes are, however, available which
result in constraints on the Hubble constant together with other parameters, notably
compared to
those which are obtainable by other methods. Other observing programmes are, however, available which
result in constraints on the Hubble constant together with other parameters, notably 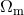 ,
, 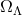 and
and 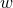 (the dark energy equation of state parameter defined in Section 1.2); we can either regard
(the dark energy equation of state parameter defined in Section 1.2); we can either regard
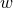 as a constant or allow a variation with redshift. We sketch these briefly here; a full review
of all programmes addressing cosmic acceleration can be found in the review by Weinberg et
al. [235*].
as a constant or allow a variation with redshift. We sketch these briefly here; a full review
of all programmes addressing cosmic acceleration can be found in the review by Weinberg et
al. [235*].
The first such supplementary programme is the study of type Ia supernovae, which as we
have seen function as standard candles (or at least easily calibratable candles). They therefore
determine the luminosity distance 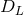 . Studies of SNe Ia were the first indication that
. Studies of SNe Ia were the first indication that 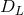 varies with
varies with  in such a way that an acceleration term, corresponding to a non-zero
in such a way that an acceleration term, corresponding to a non-zero 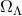 is
required [157, 158, 169], a discovery that won the 2011 Nobel Prize in physics. This determination of
luminosity distance gives constraints in the
is
required [157, 158, 169], a discovery that won the 2011 Nobel Prize in physics. This determination of
luminosity distance gives constraints in the 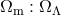 plane, which are more or less orthogonal to
the CMB constraints. Currently, the most complete samples of distant SNe come from SDSS
surveys at low redshift (
plane, which are more or less orthogonal to
the CMB constraints. Currently, the most complete samples of distant SNe come from SDSS
surveys at low redshift (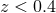 ) [73, 182, 89, 109], the ESSENCE survey at moderate redshift
(
) [73, 182, 89, 109], the ESSENCE survey at moderate redshift
(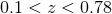 ) [135, 238], the SNLS surveys at
) [135, 238], the SNLS surveys at 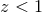 [40] and high-redshift (
[40] and high-redshift (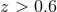 ) HST surveys
[171, 46, 208]. In the future, surveys in the infrared should be capable of extending the redshift range
further [175].
) HST surveys
[171, 46, 208]. In the future, surveys in the infrared should be capable of extending the redshift range
further [175].
The second important programme is the measurement of structure at more recent epochs than the epoch
of recombination using the characteristic length scale frozen into the structure of matter at
recombination (Section 4.1). This is manifested in the real Universe by an expected preferred correlation
length of 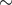 100 Mpc between observed baryon structures, otherwise known as galaxies.
These baryon acoustic oscillations (BAOs) measure a standard rod, and constrain the distance
measure
100 Mpc between observed baryon structures, otherwise known as galaxies.
These baryon acoustic oscillations (BAOs) measure a standard rod, and constrain the distance
measure 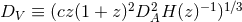 (e.g. [56*]). The largest sample available for such studies
comes from luminous red galaxies (LRGs) in the Sloan Digital Sky Survey [240]. The expected
signal was first found [56] in the form of an increased power in the cross-correlation between
galaxies at separations of about 100 Mpc, and corresponds to an effective measurement of angular
diameter distance to a redshift
(e.g. [56*]). The largest sample available for such studies
comes from luminous red galaxies (LRGs) in the Sloan Digital Sky Survey [240]. The expected
signal was first found [56] in the form of an increased power in the cross-correlation between
galaxies at separations of about 100 Mpc, and corresponds to an effective measurement of angular
diameter distance to a redshift 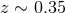 . Since then, this characteristic distance has been
found in other samples at different redshifts, 6dFGS at
. Since then, this characteristic distance has been
found in other samples at different redshifts, 6dFGS at 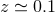 [15*], further SDSS work at
[15*], further SDSS work at
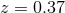 [148*] and by the BOSS and WiggleZ collaborations at
[148*] and by the BOSS and WiggleZ collaborations at 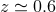 [19*, 6*]. It has also
been observed in studies of the Ly
[19*, 6*]. It has also
been observed in studies of the Ly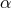 forest [31, 199, 48]. In principle, provided the data are
good enough, the BAO can be studied separately in the radial and transverse directions, giving
separate constraints on
forest [31, 199, 48]. In principle, provided the data are
good enough, the BAO can be studied separately in the radial and transverse directions, giving
separate constraints on 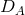 and
and 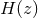 [184, 26] and hence more straightforward and accurate
cosmology.
[184, 26] and hence more straightforward and accurate
cosmology.
There are a number of other programmes that constrain combinations of cosmological parameters, which
can break degeneracies involving 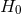 . Weak-lensing observations have progressed very substantially over
the last decade, after a large programme of quantifying and reducing systematic errors; these observations
consist of measuring shapes of large numbers of galaxies in order to extract the small shearing signal
produced by matter along the line of sight. The quantity directly probed by such observations is a
combination of
. Weak-lensing observations have progressed very substantially over
the last decade, after a large programme of quantifying and reducing systematic errors; these observations
consist of measuring shapes of large numbers of galaxies in order to extract the small shearing signal
produced by matter along the line of sight. The quantity directly probed by such observations is a
combination of 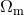 and
and 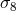 , the rms density fluctuation at a scale of
, the rms density fluctuation at a scale of 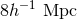 . State-of-the-art
surveys include the CFHT survey [85, 110] and SDSS-based surveys [125]. Structure can also
be mapped using Lyman-
. State-of-the-art
surveys include the CFHT survey [85, 110] and SDSS-based surveys [125]. Structure can also
be mapped using Lyman-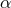 forest observations. The spectra of distant quasars have deep
absorption lines corresponding to absorbing matter along the line of sight. The distribution of these
lines measures clustering of matter on small scales and thus carries cosmological information
(e.g. [226, 133]). Clustering on small scales [215] can be mapped, and the matter power spectrum can be
measured, using large samples of galaxies, giving constraints on combinations of
forest observations. The spectra of distant quasars have deep
absorption lines corresponding to absorbing matter along the line of sight. The distribution of these
lines measures clustering of matter on small scales and thus carries cosmological information
(e.g. [226, 133]). Clustering on small scales [215] can be mapped, and the matter power spectrum can be
measured, using large samples of galaxies, giving constraints on combinations of 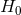 ,
, 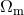 and
and
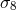 .
.
4.2.1 Combined constraints
As already mentioned, Planck observations of the CMB alone are capable of supplying a good constraint on
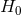 , given three assumptions: the curvature of the Universe,
, given three assumptions: the curvature of the Universe, 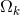 , is zero, that dark energy is a
cosmological constant (
, is zero, that dark energy is a
cosmological constant (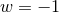 ) and that it is independent of redshift (
) and that it is independent of redshift (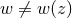 ). In general, every
other accurate measurement of a combination of cosmological parameters allows one to relax one of the
assumptions. For example, if we admit the BAO data together with the CMB, we can allow
). In general, every
other accurate measurement of a combination of cosmological parameters allows one to relax one of the
assumptions. For example, if we admit the BAO data together with the CMB, we can allow 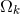 to be a
free parameter [216, 6*, 2*]. Using earlier WMAP data for the CMB,
to be a
free parameter [216, 6*, 2*]. Using earlier WMAP data for the CMB, 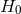 is derived to be
is derived to be
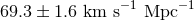 [134, 6*], which does not change significantly using Planck data
(
[134, 6*], which does not change significantly using Planck data
(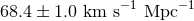 [2*]); the curvature in each case is tightly constrained (to
[2*]); the curvature in each case is tightly constrained (to 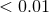 ) and
consistent with zero. If we introduce supernova data instead of BAO data, we can obtain
) and
consistent with zero. If we introduce supernova data instead of BAO data, we can obtain 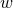 provided that
provided that
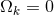 [235*, 2*] and this is found to be consistent with
[235*, 2*] and this is found to be consistent with 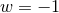 within errors of about
0.1 – 0.2 [2*].
within errors of about
0.1 – 0.2 [2*].
If we wish to proceed further, we need to introduce additional data to get tight constraints on 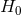 . The
obvious option is to use both BAO and SNe data together with the CMB, which results in
. The
obvious option is to use both BAO and SNe data together with the CMB, which results in
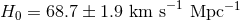 [19*] and
[19*] and 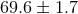 (see Table 4 of [6*]) using the WMAP CMB
constraints. Such analyses continue to give low errors on
(see Table 4 of [6*]) using the WMAP CMB
constraints. Such analyses continue to give low errors on 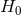 even allowing for a varying
even allowing for a varying 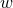 in a non-flat
universe, although they do use the results from three separate probes to achieve this. Alternatively,
extrapolation of the BAO results to
in a non-flat
universe, although they do use the results from three separate probes to achieve this. Alternatively,
extrapolation of the BAO results to 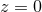 give
give 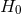 directly [55, 15*, 235] because the BAO measures a
standard ruler, and the lower the redshift, the purer the standard ruler’s dependence on the Hubble
constant becomes, independent of other elements in the definition of Hubble parameter such
as
directly [55, 15*, 235] because the BAO measures a
standard ruler, and the lower the redshift, the purer the standard ruler’s dependence on the Hubble
constant becomes, independent of other elements in the definition of Hubble parameter such
as 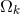 and
and 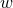 . The lowest-redshift BAO measurement is that of the 6dF, which suggests
. The lowest-redshift BAO measurement is that of the 6dF, which suggests
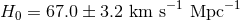 [15*].
[15*].