List of Footnotes
| 1 | See [105*] and references therein, e.g., [27], for discussion of the details of the interpretation of redshift in an
expanding Universe. The first level of sophistication involves maintaining the GR principle that space is locally
Minkowskian, so that in a small region of space all effects must reduce to SR (for instance, in Peacock’s [155*]
example, the expansion of the Universe does not imply that a long-lived human will grow to four metres tall
in the next 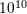 years). Redshift can be thought of as a series of transformations in photon wavelengths
between an infinite succession of closely-separated observers, resulting in an overall wavelength shift between two
observers with a finite separation and therefore an associated “velocity”. The second level of sophistication is
to ask what this velocity actually represents. [105] calculates the ratio of photon wavelength shifts between
pairs of fundamental observers to the shifts in their proper separation in the presence of arbitrary gravitational
fields, and shows that this ratio only corresponds to the purely dynamical result if the gravitational tide is
constant. years). Redshift can be thought of as a series of transformations in photon wavelengths
between an infinite succession of closely-separated observers, resulting in an overall wavelength shift between two
observers with a finite separation and therefore an associated “velocity”. The second level of sophistication is
to ask what this velocity actually represents. [105] calculates the ratio of photon wavelength shifts between
pairs of fundamental observers to the shifts in their proper separation in the presence of arbitrary gravitational
fields, and shows that this ratio only corresponds to the purely dynamical result if the gravitational tide is
constant. |
|
| 2 | This is known in the literature as the “instability strip” and is almost, but not quite, parallel to the luminosity axis on the H-R diagram. In normal stars, any compression of the star, and the associated rise in temperature, results in a decrease in opacity; the resulting escape of photons produces expansion and cooling. For stars in the instability strip, a layer of partially ionized He close to the surface causes opacity to rise instead of falling with an increase in temperature, producing a degree of positive feedback and consequently oscillations. The instability strip has a finite width, which causes a small degree of dispersion in period–luminosity correlations among Cepheids. | |
| 3 | There are numerous subtle and less-subtle biases in distance measurement; see [213] for a blow-by-blow account. The simplest bias, the “classical” Malmquist bias, arises because, in any population of objects with a distribution in intrinsic luminosity, only the brighter members of the population will be seen at large distances. The result is that the inferred average luminosity is greater than the true luminosity, biasing distance measurements towards the systematically short. The Behr bias [12*] from 1951 is a distance-dependent version of the Malmquist bias, namely that at higher distances, increasingly bright galaxies will be missing from samples. This leads to an overestimate of the average brightness of the standard candle which becomes worse at higher distance. | |
| 4 | Cepheids come in two flavours: type I and type II, corresponding to population I and II stars. Population II stars are an
earlier metal-poor generation of stars, which formed after the hypothetical, truly primordial Population III stars, but before
later-generation Population I stars like the Sun which contain significant extra amounts of elements other than hydrogen and
helium due to enrichment of the ISM by supernovae in the meantime. The name “Cepheid” derives from the fact that the star
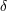 Cephei was the first to be identified (by Goodricke in 1784). Population II Cepheids are sometimes known as W Virginis
stars, after their prototype, W Vir, and a W Vir star is typically a factor of 3 fainter than a classical Cepheid of the same
period. Cephei was the first to be identified (by Goodricke in 1784). Population II Cepheids are sometimes known as W Virginis
stars, after their prototype, W Vir, and a W Vir star is typically a factor of 3 fainter than a classical Cepheid of the same
period. |
|
| 5 | The conclusion of the latter, that based on median statistics of the Huchra compilation, 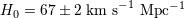 , is
slightly scary in retrospect given the Planck value of , is
slightly scary in retrospect given the Planck value of 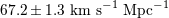 for a flat Universe [2*]. for a flat Universe [2*]. |
|
| 6 | Historically, the Hubble constant has often been quoted as 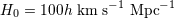 , as a way of maintaining
agnosticism in an era where observations allowed a wide range in , as a way of maintaining
agnosticism in an era where observations allowed a wide range in 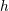 . This is largely disappearing, but papers using . This is largely disappearing, but papers using 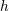 can
be hard to interpret [42] can
be hard to interpret [42] |
|
| 7 | For example, one topic that may merit more than a footnote in the future is the study of cosmology using gravitational
waves. In particular, a coalescing binary system consisting of two neutron stars produces gravitational waves, and under those
circumstances the measurement of the amplitude and frequency of the waves determines the distance to the object
independently of the stellar masses [193]. This was studied in more detail by [36] and extended to more massive black-hole
systems [90, 45]. More massive coalescing signals produce lower-frequency gravitational-wave signals, which can be
detected with the proposed LISA space-based interferometer ( http://lisa.nasa.gov/documentation.html). The
major difficulty is obtaining the redshift measurement to go with the distance estimate, since the galaxy in
which the coalescence event has taken place must be identified. Given this, however, the precision of the http://lisa.nasa.gov/documentation.html). The
major difficulty is obtaining the redshift measurement to go with the distance estimate, since the galaxy in
which the coalescence event has taken place must be identified. Given this, however, the precision of the 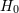 measurement is limited only by weak gravitational lensing along the line of sight, and even this is reducible by
observations of multiple systems or detailed investigations of matter along the line of sight.
measurement is limited only by weak gravitational lensing along the line of sight, and even this is reducible by
observations of multiple systems or detailed investigations of matter along the line of sight. 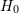 determinations
to determinations
to 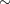 2% should be possible, but depend on the launch of LISA or a similar mission. This is an event that
is probably decades away, although a pathfinder mission to test some of the technology is due for launch in
2015. 2% should be possible, but depend on the launch of LISA or a similar mission. This is an event that
is probably decades away, although a pathfinder mission to test some of the technology is due for launch in
2015. |
|
| 8 | Strictly speaking, provided we ignore effects to do with curvature of the Universe. | |
| 9 | An isothermal model is one in which the projected surface mass density decreases as 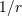 . An isothermal galaxy will have
a flat rotation curve, as is observed in many galaxies. . An isothermal galaxy will have
a flat rotation curve, as is observed in many galaxies. |
|
| 10 | Essentially all radio time delays have come from the VLA, although monitoring programmes with MERLIN have also been attempted. | |
| 11 | The redshifts of the lens and source also need to be known, as does the position of the centre of the lens galaxy; this measurement is not always a trivial proposition [241]. | |
| 12 | As discussed extensively in [113*, 117], this is not a global degeneracy, but arises because the lensed images tell you about the mass distribution in the annulus centred on the galaxy and with inner and outer radii defined by the inner and outer images. Kochanek [113] derives detailed expressions for the time delay in terms of the central underlying and controlling parameter, the surface density in this annulus [76*]. | |
| 13 | The programme, known as H0LiCOW, is now continuing in order to measure time delays, improve models and derive
further 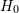 values for more lenses. values for more lenses. |
|
| 14 | Because of the expansion of the Universe, there is a time dilation of a factor 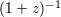 which must be applied to
timescales measured at cosmological distances before these are used for such comparisons. which must be applied to
timescales measured at cosmological distances before these are used for such comparisons. |
|
| 15 | The effective radius is the radius from within which half the galaxy’s light is emitted. | |
| 16 | Nearly all Cepheids measured in galaxies containing SN Ia have periods 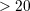 days, so the usual sense of the effect is
that Galactic Cepheids of a given period are brighter than LMC Cepheids. days, so the usual sense of the effect is
that Galactic Cepheids of a given period are brighter than LMC Cepheids. |
|
| 17 | Here, as elsewhere in astronomy, the term “metals” is used to refer to any element heavier than helium. Metallicity is usually quoted as 12+log(O/H), where O and H are the abundances of oxygen and hydrogen. | |
| 18 | The details are discussed in more detail in an earlier version of this review [102]. | |
| 19 | This characteristic size is about 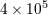 light years at recombination, corresponding to an angular scale of about light years at recombination, corresponding to an angular scale of about 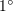 on
the sky. The fact that the CMB is homogeneous on scales much larger than this is an illustration of the “horizon problem”
discussed in Section 1.2, and which inflation may solve. on
the sky. The fact that the CMB is homogeneous on scales much larger than this is an illustration of the “horizon problem”
discussed in Section 1.2, and which inflation may solve. |
|
| 20 | See  http://background.uchicago.edu/~whu/intermediate/intermediate.html for a much longer exposition and
tutorial on all these areas. http://background.uchicago.edu/~whu/intermediate/intermediate.html for a much longer exposition and
tutorial on all these areas. |
|
| 21 | See Table 2 of [2*] for a full list. |
