List of Footnotes
| 1 |  |
“[D]er Gravitationsradius des zur Messung dienenden Probekörpers (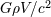 ) soll keineswegs größer als seine
linearen Abmessungen ( ) soll keineswegs größer als seine
linearen Abmessungen (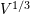 ) sein; daraus entsteht eine obere Grenze für seine Dichte ( ) sein; daraus entsteht eine obere Grenze für seine Dichte (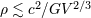 ). Die
Messungsmöglichkeiten sind also in dem Gebiet noch mehr beschränkt als es sich aus den quantenmechanischen
Vertauschungsrelationen schliessen läßt. Ohne eine tiefgreifende Änderung der klassischen Begriffe, scheint es daher
kaum möglich, die Quantentheorie der Gravitation auch auf dieses Gebiet auszudehnen.” ). Die
Messungsmöglichkeiten sind also in dem Gebiet noch mehr beschränkt als es sich aus den quantenmechanischen
Vertauschungsrelationen schliessen läßt. Ohne eine tiefgreifende Änderung der klassischen Begriffe, scheint es daher
kaum möglich, die Quantentheorie der Gravitation auch auf dieses Gebiet auszudehnen.” |
| 2 | Translations from German to English: SH. | |
| 3 |  |
“Wenn die Explosionen tatsächlich existieren und die für die Konstante 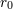 eigentlich charakeristischen Prozesse
darstellen, so vermitteln sie vielleicht ein erstes, noch unklares Verständnis der unanschaulichen Züge, die mit der
Konstanten eigentlich charakeristischen Prozesse
darstellen, so vermitteln sie vielleicht ein erstes, noch unklares Verständnis der unanschaulichen Züge, die mit der
Konstanten 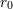 verbunden sind. Diese sollten sich ja wohl zunächst darin äußern, daß die Messung einer den
Wert verbunden sind. Diese sollten sich ja wohl zunächst darin äußern, daß die Messung einer den
Wert 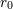 unterschreitenden Genauigkeit zu Schwierigkeiten führt…[D]ie Explosionen [würden] dafür sorgen…, daß
Ortsmessungen mit einer unterschreitenden Genauigkeit zu Schwierigkeiten führt…[D]ie Explosionen [würden] dafür sorgen…, daß
Ortsmessungen mit einer 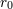 unterschreitenden Genauigkeit unmöglich sind.” unterschreitenden Genauigkeit unmöglich sind.” |
| 4 |  |
“Der Umstand, daß [die Plancklänge] wesentlich kleiner ist als 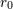 , gibt uns das Recht, von den durch die
Gravitation bedingten unanschaulichen Zügen der Naturbeschreibung zunächst abzusehen, da sie – wenigstens
in der Atomphysik – völlig untergehen in den viel gröberen unanschaulichen Zügen, die von der universellen
Konstanten , gibt uns das Recht, von den durch die
Gravitation bedingten unanschaulichen Zügen der Naturbeschreibung zunächst abzusehen, da sie – wenigstens
in der Atomphysik – völlig untergehen in den viel gröberen unanschaulichen Zügen, die von der universellen
Konstanten 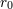 herrühren. Es dürfte aus diesen Gründen wohl kaum möglich sein, die elektrischen und die
Gravitationserscheinungen in die übrige Physik einzuordnen, bevor die mit der Länge herrühren. Es dürfte aus diesen Gründen wohl kaum möglich sein, die elektrischen und die
Gravitationserscheinungen in die übrige Physik einzuordnen, bevor die mit der Länge 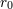 zusammenhängenden
Probleme gelöst sind.” zusammenhängenden
Probleme gelöst sind.” |
| 5 |  |
“Mir ist es bisher nicht gelungen, solchen Vertauschungs-Relationen einen vernünftigen mathematischen Sinn zuzuordnen…Fällt Ihnen oder Pauli nicht vielleicht etwas über den mathematischen Sinn solcher Vertauschungs-Relationen ein?” |
| 6 | The story has been told [313] that Peierls asked Pauli, Pauli passed the question on to his colleague Oppenheimer, who asked his student Hartland Snyder. However, in a 1946 letter to Pauli [289], Snyder encloses his paper without any mention of it being an answer to a question posed to him by others. | |
| 7 | Though the hope of a lowered Planck scale pushing quantum gravitational effects into the reach of the Large Hadron Collider seems, at the time of writing, to not have been fulfilled. | |
| 8 | In the classical theory, inside the horizon lies a singularity. This singularity is expected to be avoided in quantum gravity, but how that works or doesn’t work is not relevant in the following. | |
| 9 | An example of a different choice of basis can be found in [314]. | |
| 10 | The word ‘effective’ should here not be read as a technical term. | |
| 11 | According to the Hellinger–Toeplitz theorem, an everywhere-defined symmetric operator on a Hilbert space is necessarily bounded. Since some operators in quantum mechanics are unbounded, one is required to deal with wave functions that are not square integrable. The same consideration applies here. | |
| 12 | The Lorentz group has a second Casimir operator, which is the length of the Pauli–Lubanski pseudovector. It can be identified by it being a function of the angular momentum operator. | |
| 13 | Though it has meanwhile been shown that the fixed point behavior can be found also in the Lorentzian case [218]. |

