5.3 Cosmological redshift-space distortion
Consider a spherical object at high redshift. If the wrong cosmology is assumed in interpreting the
distance-redshift relation along the line of sight and in the transverse direction, the sphere will appear
distorted. Alcock and Paczynski [2] pointed out that this curvature effect could be used to estimate
the cosmological constant. Matsubara and Suto [54] and Ballinger, Peacock, and Heavens [3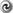 ]
developed a theoretical framework to describe the geometrical distortion effect (cosmological redshift
distortion) in the two-point correlation function and the power spectrum of distant objects,
respectively. Certain studies were less optimistic than others about the possibility of measuring this
Alcock–Paczynski effect. For example, Ballinger, Peacock, and Heavens [3] argued that the
geometrical distortion could be confused with the dynamical redshift distortions caused by
peculiar velocities and characterized by the linear theory parameter
]
developed a theoretical framework to describe the geometrical distortion effect (cosmological redshift
distortion) in the two-point correlation function and the power spectrum of distant objects,
respectively. Certain studies were less optimistic than others about the possibility of measuring this
Alcock–Paczynski effect. For example, Ballinger, Peacock, and Heavens [3] argued that the
geometrical distortion could be confused with the dynamical redshift distortions caused by
peculiar velocities and characterized by the linear theory parameter 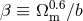 . Matsubara
and Szalay [55, 56] showed that the typical SDSS and 2dF samples of normal galaxies at low
redshift (
. Matsubara
and Szalay [55, 56] showed that the typical SDSS and 2dF samples of normal galaxies at low
redshift (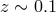 ) have sufficiently low signal-to-noise, but they are too shallow to detect the
Alcock–Paczynski effect. On the other hand, the quasar SDSS and 2dFGRS surveys are at a useful
redshift, but they are too sparse. A more promising sample is the SDSS Luminous Red Galaxies
survey (out to redshift
) have sufficiently low signal-to-noise, but they are too shallow to detect the
Alcock–Paczynski effect. On the other hand, the quasar SDSS and 2dFGRS surveys are at a useful
redshift, but they are too sparse. A more promising sample is the SDSS Luminous Red Galaxies
survey (out to redshift 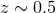 ) which turns out to be optimal in terms of both depth and
density.
) which turns out to be optimal in terms of both depth and
density.
While this analysis is promising, it remains to be tested if non-linear clustering and complicated biasing
(which is quite plausible for red galaxies) would not ‘contaminate’ the measurement of the equation of state.
Even if the Alcock–Paczynski test turns out to be less accurate than other cosmological tests (e.g.,
CMB and SN Ia), the effect itself is an interesting and important ingredient in analyzing the
clustering pattern of galaxies at high redshifts. We shall now present the formalism for this
effect.
Due to a general-relativistic effect through the geometry of the Universe, the observable separations
perpendicular and parallel to the line-of-sight direction, 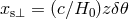 and
and 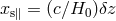 , are
mapped differently to the corresponding comoving separations in real space
, are
mapped differently to the corresponding comoving separations in real space 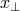 and
and 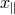 :
:
with 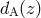 being the angular diameter distance. The difference between
being the angular diameter distance. The difference between 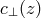 and
and 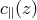 generates an
apparent anisotropy in the clustering statistics, which should be isotropic in the comoving space. Then the
power spectrum in cosmological redshift space
generates an
apparent anisotropy in the clustering statistics, which should be isotropic in the comoving space. Then the
power spectrum in cosmological redshift space 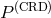 is related to
is related to 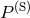 defined in the comoving
redshift space as
where the first factor comes from the Jacobian of the volume element
defined in the comoving
redshift space as
where the first factor comes from the Jacobian of the volume element 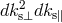 , and
, and 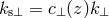 and
and
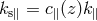 are the wavenumber perpendicular and parallel to the line-of-sight direction.
are the wavenumber perpendicular and parallel to the line-of-sight direction.
Using Equation (131), Equation (156) reduces to
where
Figure 16 shows anisotropic power spectra 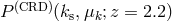 . As specific examples, we
consider SCDM, LCDM, and OCDM models, which have
. As specific examples, we
consider SCDM, LCDM, and OCDM models, which have 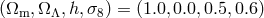 ,
,
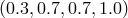 , and
, and 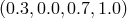 , respectively. Clearly the linear theory predictions
(
, respectively. Clearly the linear theory predictions
(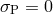 ; top panels) are quite different from the results of
; top panels) are quite different from the results of 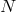 -body simulations (bottom panels),
indicating the importance of the nonlinear velocity effects (
-body simulations (bottom panels),
indicating the importance of the nonlinear velocity effects (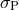 computed according to [58]; middle
panels).
computed according to [58]; middle
panels).
Next we decompose the power spectrum into harmonics,
where 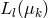 are the
are the 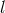 -th order Legendre polynomials. Similarly, the two-point correlation function is
decomposed as
using the direction cosine
-th order Legendre polynomials. Similarly, the two-point correlation function is
decomposed as
using the direction cosine 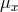 between the separation vector and the line-of-sight. The above multipole
moments satisfy the following relations:
with
between the separation vector and the line-of-sight. The above multipole
moments satisfy the following relations:
with 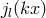 being spherical Bessel functions. Substituting
being spherical Bessel functions. Substituting 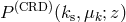 in Equation (159) yields
in Equation (159) yields
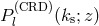 , and then
, and then 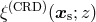 can be computed from Equation (161).
can be computed from Equation (161).
A comparison of the monopoles and quadrupoles from simulations and model predictions exhibits how
the results are sensitive to the cosmological parameters, which in turn may put potentially useful
constraints on 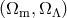 . Figure 17 indicates the feasibility, which interestingly results in a constraint
fairly orthogonal to that from the supernovae Ia Hubble diagram.
. Figure 17 indicates the feasibility, which interestingly results in a constraint
fairly orthogonal to that from the supernovae Ia Hubble diagram.
![]() and
and ![]() , are
mapped differently to the corresponding comoving separations in real space
, are
mapped differently to the corresponding comoving separations in real space ![]() and
and ![]() :
:
![]() ), Equation (156
), Equation (156![]() ) reduces to
) reduces to ![]() shows anisotropic power spectra
shows anisotropic power spectra ![]() . As specific examples, we
consider SCDM, LCDM, and OCDM models, which have
. As specific examples, we
consider SCDM, LCDM, and OCDM models, which have ![]() ,
,
![]() , and
, and ![]() , respectively. Clearly the linear theory predictions
(
, respectively. Clearly the linear theory predictions
(![]() ; top panels) are quite different from the results of
; top panels) are quite different from the results of ![]() -body simulations (bottom panels),
indicating the importance of the nonlinear velocity effects (
-body simulations (bottom panels),
indicating the importance of the nonlinear velocity effects (![]() computed according to [58]; middle
panels).
computed according to [58]; middle
panels).
![]() . Figure 17
. Figure 17![]() indicates the feasibility, which interestingly results in a constraint
fairly orthogonal to that from the supernovae Ia Hubble diagram.
indicates the feasibility, which interestingly results in a constraint
fairly orthogonal to that from the supernovae Ia Hubble diagram.