Volume 2,
Issue 2, 2001
Article
19
|
MONOTONIC REFINEMENTS OF A KY FAN INEQUALITY
KWOK
KEI
CHONG
DEPARTMENT OF APPLIED MATHEMATICS
THE HONG KONG POLYTECHNIC UNIVERSITY
HUNG HOM, KOWLOON
HONG KONG, CHINA
E-Mail: makkchon@inet.polyu.edu.hk
Received 3 October, 2000; accepted 2 February, 2001.
Communicated by: F. Qi
|
ABSTRACT.
It is well-known that inequalities between means play a very important role
in many branches of mathematics. Please refer to [1,3,7], etc. The main aims
of the present article are:
- (i)
- to show that there are monotonic and continuous functions
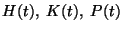 and and 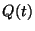 on on
![$ \left[ 0,1\right] $](../abstract/035_00_ab/img3.gif) such that for all such that for all
![$ %%
t\in \lbrack 0,1],$](../abstract/035_00_ab/img4.gif) and
and
where
 and and 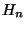 are respectively the weighted arithmetic,
geometric and harmonic means of the positive numbers are respectively the weighted arithmetic,
geometric and harmonic means of the positive numbers
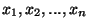 in
in ![$(0,1/2],$](../abstract/035_00_ab/img10.gif) with positive weights with positive weights
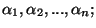 while while
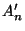 and and
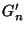 are respectively the
weighted arithmetic and geometric means of the numbers are respectively the
weighted arithmetic and geometric means of the numbers
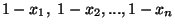 with the same positive weights with the same positive weights
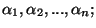
- (ii)
- to present more general monotonic refinements for the Ky Fan
inequality as well as some inequalities involving means; and
- (iii)
- to present some generalized and new inequalities in this connection.
[1] H. ALZER,
Inequalities for arithmetic, geometric and harmonic means, Bull.
London Math. Soc.,
22 (1990),
362–366.
[3] P.S. BULLEN, D.S.
MITRINOVIC and J.E. PECARIC,
Means and
Their Inequalities,
ReiddelDordrecht, 1988.
[7] A.M. FINK, J.E.
PECARIC and D.S.
MITRINOVIC, Classical
and New Inequalities in Analysis,
Kluwer Academic
Publishers, 1993.
Key words:
Ky Fan inequality, Monotonic refinements of
inequalities, Arithmetic, geometric and harmonic
means.
2000 Mathematics Subject
Classification:
26D15, 26A48
|
|
|
Download this article (PDF):
|
Suitable for a printer: 
Suitable for a monitor:
 |
To view these files we
recommend you save them to your file system and then view by using
the Adobe Acrobat Reader.
That is, click on the icon using the 2nd mouse button and
select "Save Target As..." (Microsoft Internet
Explorer) or "Save Link As..." (Netscape
Navigator).
See our PDF pages for more
information.
|
|
|
Other issues
-
Volume 1, Issue 1, 2000
-
Volume 1, Issue
2, 2000
-
Volume 2, Issue
1, 2001
-
Volume 2, Issue
2, 2001
-
Volume 2, Issue
3, 2001
-
Volume 3, Issue
1, 2002
-
Volume 3, Issue
2, 2002
-
Volume 3, Issue
3, 2002
-
Volume 3, Issue
4, 2002
-
Volume 3, Issue
5, 2002
-
Volume 4, Issue
1, 2003
-
Volume 4, Issue
2, 2003
-
Volume 4, Issue
3, 2003
-
Volume 4, Issue
4, 2003
-
Volume 4, Issue
5, 2003
|
|

