|
If
 ,
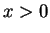is a Hardy-type operator defined on the cone of monotone functions, then weight
characterizations for which the modular inequality
holds, are given for a large class of modular functions  .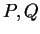
Specifically, these functions need not both be 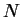 -functions,
and the class includes the case where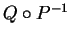 
is concave. Our results generalize those in [7,24], where the case
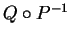convex, with 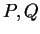, 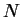-function
was studied. Applications involving the Hardy averaging operator, its dual, the
Hardy-Littlewood maximal function, and the Hilbert transform are also given.
[7] P. DRÁBEK, H.P. HEINIG AND A. KUFNER, Weighted modular inequalities for
monotone functions, J. of Inequal. and Appl., 1 (1997), 183–197.
[24] J.Q. SUN, The modular inequalities for a class of convolutions operators on
monotone functions, Proc. Amer. Math. Soc., 125 (1997), 2293–2305.
Key words:
Hardy-type operators,
modular
inequalities, weights,
N-functions, characterizations,
Orlicz-Lorentz.
2000 Mathematics Subject
Classification:
26D15, 42B25,
26A33, 46E30.
|
|
![\begin{displaymath}
Q^{-1}\left( \int_{0}^{\infty }Q[\theta (Kf)]w\right) \leq P^{-1}\left(
\int_{0}^{\infty }P[Cf]v\right)
\end{displaymath}](010_99/img3.gif){kind=small}
R.P.
Agarwal