Воробьев Н. Т., Марцинкевич А. В.
Конечные π-группы с нормальными инъекторамиПусть
— множество всех простых чисел и
≠ π
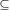
. Класс Фиттинга
≠ (1) называют нормальным в классе
π всех конечных разрешимых π-групп или π-нормальным, если
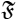
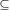
π и для любой G

π ее
-инъекторы являются нормальными подгруппами G. Изучаются свойства π-нормальных классов Фиттинга: в терминах операторов Локетта доказан критерий π-нормальности произведения классов Фиттинга. π-Нормальный класс Фиттинга называется нормальным, если π =
. Решетка всех разрешимых нормальных классов Фиттинга является подрешеткой решетки всех разрешимых классов Фиттинга, хотя вопрос о модулярности решетки всех разрешимых классов Фиттинга открыт (см. [1, вопрос 14.47]). Получено положительное решение аналога этого вопроса для случая
π-нормальных классов Фиттинга.
Vorob’ev N. T., Martsinkevich A. V.
Finite π-groups with normal injectorsDenote by
the set of all primes and take a nonempty set π
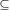
. A Fitting class
≠ (1) is callednormal in the class
π of all finite soluble π-groups or π-normal, whenever
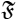
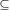
π and for every G

π its
-injectors constitute a normal subgroup of G.
We study the properties of π-normal Fitting classes. Using Lockett operators, we prove a criterion for the π-normality of products of Fitting classes. A π-normal Fitting class is normal in the case π =. The lattice of all solvable normal Fitting classes is a sublattice of the lattice of all solvable Fitting classes; but the question of modularity of the lattice of all solvable Fitting classes is open (see Question 14.47 in [1]). We obtain a positive answer to a similar question in the case of π-normal Fitting classes.
DOI 10.17377/smzh.2015.56.406
Ключевые слова: класс Фиттинга, π-нормальный класс Фиттинга, произведение классов Фиттинга, решеточное объединение классов Фиттинга.Полный текст статьи / Full texts:
![]()