Романов В. Г.
Оценка устойчивости решения в обратной задаче электродинамикиРассматривается интегродифференциальная система уравнений электродинамики, которая соответствует немагнитной среде, обладающей дисперсией. Для этой системы изучается задача об определении пространственной части ядра, входящего в интегральный член уравнения. Это соответствует отысканию той части диэлектрической проницаемости, которая нелинейно зависит от частоты электромагнитной волны. Предполагается, что носитель диэлектрической проницаемости содержится в некоторой компактной области Ω
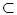
3. Для отыскания ее внутри Ω задается информация о решении соответствующей прямой задачи для системы уравнений электродинамики на всей границе области Ω для некоторого конечного временного интервала. В предположении, что временной интервал достаточно велик, установлена оценка условной устойчивости решения рассматриваемой обратной задачи.
Romanov V. G.
A stability estimate for a solution to an inverse problem of electrodynamicsWe consider the integrodifferential system of equations of electrodynamics which corresponds to a dispersive nonmagnetic medium. For this system we study the problem of determining the spatial part of the kernel of the integral term. This corresponds to finding the part of dielectric permittivity depending nonlinearly on the frequency of the electromagnetic wave. We assume that the support of dielectric permittivity lies in some compact domain Ω
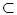
3. In order to find it inside Ω we start with known data about the solution to the corresponding direct problem for the equations of electrodynamics on the whole boundary of Ω for some finite time interval. On assuming that the time interval is sufficiently large we estimate the conditional stability of the solution to this inverse problem.
Полный текст статьи / Full texts:
![]()