Асылбеков Ж. А., Зубов В. Н., Ульянов В. В.
Об аппроксимации некоторых статистик критериев согласия для случая дискретных трехмерных данныхИсследуется скорость слабой сходимости распределений статистик {tλ(Υ), λ
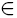
} критериев согласия со степенными мерами расхождения к хи-квадрат распределению. Статистики построены по n наблюдениям случайной величины с тремя возможными исходами. Доказано, что
Pr (tλ(Υ) < c) = G2(c) + O (n−50/73(log n)315/146 ),
где G2(c) — функция распределения хи-квадрат случайной величины с двумя степенями свободы. В доказательстве используется теорема М. Н. Хаксли (1993 г.) о приближении числа точек с целочисленными координатами, содержащихся в выпуклом множестве с гладкой границей на плоскости, его площадью.
Asylbekov Zh. A., Zubov V. N., Ulyanov V. V.
On approximating some statistics of goodness-of-fit tests in the case of three-dimensional discrete dataWe study the rate of weak convergence of the distributions of the statistics {tλ(Υ), λ
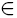
} from the power divergence family of statistics to the χ2 distribution. The statistics are constructed from n observations of a random variable with three possible values. We show that
Pr (tλ(Υ) < c) = G2(c) + O (n−50/73(log n)315/146 ),
whereG2(c) is the χ2 distribution function of a random variable with two degrees of freedom. In the proof we use Huxley’s theorem of 1993 on approximating the number of integer points in a plane convex set with smooth boundary by the area of the set.
Полный текст статьи / Full texts:
![]()