3.1 Gaussian random field
Consider the density contrast 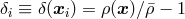 defined at the comoving position
defined at the comoving position 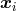 . The
density field is regarded as a stochastic variable, and thus forms a random field. The conventional
assumption is that the primordial density field (in its linear regime) is Gaussian, i.e., its
. The
density field is regarded as a stochastic variable, and thus forms a random field. The conventional
assumption is that the primordial density field (in its linear regime) is Gaussian, i.e., its 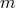 -point joint
probability distribution obeys the multi-variate Gaussian,
for an arbitrary positive integer
-point joint
probability distribution obeys the multi-variate Gaussian,
for an arbitrary positive integer 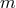 . Here
. Here 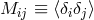 is the covariance matrix, and
is the covariance matrix, and 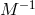 is its
inverse. Since
is its
inverse. Since 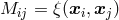 , Equation (71) implies that the statistical nature of the Gaussian density
field is completely specified by the two-point correlation function
, Equation (71) implies that the statistical nature of the Gaussian density
field is completely specified by the two-point correlation function 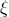 and its linear combination (including
its derivative and integral). For an extensive discussion of the cosmological Gaussian density field,
see [4
and its linear combination (including
its derivative and integral). For an extensive discussion of the cosmological Gaussian density field,
see [4 ].
].
The Gaussian nature of the primordial density field is preserved in its linear evolution stage, but this is
not the case in the nonlinear stage. This is clear even from the definition of the Gaussian distribution:
Equation (71) formally assumes that the density contrast distributes symmetrically in the range of
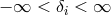 , but in the real density field
, but in the real density field 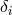 cannot be less than
cannot be less than 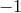 . This assumption does
not make any practical difference as long as the fluctuations are (infinitesimally) small, but
it is invalid in the nonlinear regime where the typical amplitude of the fluctuations exceeds
unity.
. This assumption does
not make any practical difference as long as the fluctuations are (infinitesimally) small, but
it is invalid in the nonlinear regime where the typical amplitude of the fluctuations exceeds
unity.
In describing linear theory of cosmological density fluctuations, the Fourier transform of the spatial
density contrast 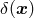
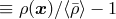 is the most basic variable:
is the most basic variable:
Since 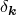 is a complex variable, it is decomposed by a set of two real variables, the amplitude
is a complex variable, it is decomposed by a set of two real variables, the amplitude 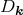 and
the phase
and
the phase 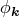 :
Then linear perturbation equation reads
Equation (75) yields
:
Then linear perturbation equation reads
Equation (75) yields 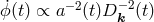 , and
, and 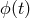 rapidly converges to a constant value. Thus
rapidly converges to a constant value. Thus 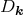 evolves following the growing solution in linear theory.
evolves following the growing solution in linear theory.
The most popular statistic of clustering in the Universe is the power spectrum of the density
fluctuations,
which measures the amplitude of the mode of the wavenumber 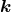 . This is the Fourier transform of the
two-point correlation function,
If the density field is globally homogeneous and isotropic (i.e., no preferred position or direction),
Equation (77) reduces to
Since the above expression is obtained after the ensemble average,
. This is the Fourier transform of the
two-point correlation function,
If the density field is globally homogeneous and isotropic (i.e., no preferred position or direction),
Equation (77) reduces to
Since the above expression is obtained after the ensemble average, 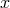 does not denote an amplitude
of the position vector, but a comoving wavelength
does not denote an amplitude
of the position vector, but a comoving wavelength 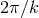 corresponding to the wavenumber
corresponding to the wavenumber
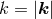 . It should be noted that neither the power spectrum nor the two-point correlation
function contains information for the phase
. It should be noted that neither the power spectrum nor the two-point correlation
function contains information for the phase 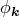 . Thus in principle two clustering patterns may be
completely different even if they have the identical two-point correlation functions. This implies the
practical importance to describe the statistics of phases
. Thus in principle two clustering patterns may be
completely different even if they have the identical two-point correlation functions. This implies the
practical importance to describe the statistics of phases 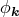 in addition to the amplitude
in addition to the amplitude 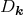 of
clustering.
of
clustering.
In the Gaussian field, however, one can directly show that Equation (71) reduces to the probability
distribution function of 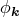 and
and 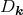 that are explicitly written as
that are explicitly written as
mutually independently of 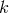 . The phase distribution is uniform, and thus does not carry information. The
above probability distribution function is also derived when the real and imaginary parts of the Fourier
components
. The phase distribution is uniform, and thus does not carry information. The
above probability distribution function is also derived when the real and imaginary parts of the Fourier
components 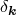 are uncorrelated and Gaussian distributed (with the dispersion
are uncorrelated and Gaussian distributed (with the dispersion 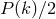 ) independently
of
) independently
of 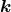 . As is expected, the distribution function (79) is completely fixed if
. As is expected, the distribution function (79) is completely fixed if 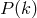 is specified. This
rephrases the previous statement that the Gaussian field is completely specified by the two-point correlation
function in real space.
is specified. This
rephrases the previous statement that the Gaussian field is completely specified by the two-point correlation
function in real space.
Incidentally the one-point phase distribution turns out to be essentially uniform even in a strongly
non-Gaussian field [81, 21]. Thus it is unlikely to extract useful information directly out of it mainly due to
the cyclic property of the phase. Very recently, however, Matsubara [51] and Hikage et al. [31] succeeded in
detecting a signature of phase correlations in Fourier modes of mass density fields induced by nonlinear
gravitational clustering using the distribution function of the phase sum of the Fourier modes for triangle
wavevectors. Several different statistics which carry the phase information have been also proposed in
cosmology, including the void probability function [97], the genus statistics [26 ], and the Minkowski
functionals [57
], and the Minkowski
functionals [57 , 76].
, 76].
![]() ) formally assumes that the density contrast distributes symmetrically in the range of
) formally assumes that the density contrast distributes symmetrically in the range of
![]() , but in the real density field
, but in the real density field ![]() cannot be less than
cannot be less than ![]() . This assumption does
not make any practical difference as long as the fluctuations are (infinitesimally) small, but
it is invalid in the nonlinear regime where the typical amplitude of the fluctuations exceeds
unity.
. This assumption does
not make any practical difference as long as the fluctuations are (infinitesimally) small, but
it is invalid in the nonlinear regime where the typical amplitude of the fluctuations exceeds
unity.
![]()
![]() is the most basic variable:
is the most basic variable: ![]() ) reduces to the probability
distribution function of
) reduces to the probability
distribution function of ![]() and
and ![]() that are explicitly written as
that are explicitly written as ![]() ], and the Minkowski
functionals [57
], and the Minkowski
functionals [57![]() , 76].
, 76].