6.2 Boundary value formulation
The vacuum and the EM equations in the presence of a Killing symmetry describe harmonic
mappings into coset manifolds, effectively coupled to three-dimensional gravity (see Section 4).
This feature is shared by a variety of other self-gravitating theories with scalar (moduli) and
Abelian vector fields (see Section 5.2), for which the field equations assume the form (32):
The current one-form 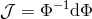 is given in terms of the hermitian matrix
is given in terms of the hermitian matrix 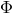 , which comprises the
norm and the generalized twist potential of the Killing field, the fundamental scalar fields and the
electric and magnetic potentials arising on the effective level for each Abelian vector field. If the
dimensional reduction is performed with respect to the axial Killing field
, which comprises the
norm and the generalized twist potential of the Killing field, the fundamental scalar fields and the
electric and magnetic potentials arising on the effective level for each Abelian vector field. If the
dimensional reduction is performed with respect to the axial Killing field 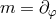 with norm
with norm
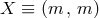 , then
, then 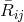 is Ricci tensor of the pseudo-Riemannian three-metric
is Ricci tensor of the pseudo-Riemannian three-metric 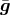 , defined by
, defined by
In the stationary and axisymmetric case under consideration, there exists, in addition
to 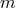 , an asymptotically time-like Killing field
, an asymptotically time-like Killing field 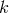 . Since
. Since 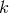 and
and 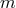 fulfill the
Frobenius integrability conditions, the spacetime metric can be written in the familiar
(2+2)-split.
Hence, the circularity property implies that
fulfill the
Frobenius integrability conditions, the spacetime metric can be written in the familiar
(2+2)-split.
Hence, the circularity property implies that
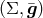 is a static pseudo-Riemannian three-dimensional manifold with metric
is a static pseudo-Riemannian three-dimensional manifold with metric
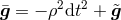 ;
;
- the connection
 is orthogonal to the two-dimensional Riemannian manifold
is orthogonal to the two-dimensional Riemannian manifold 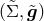 , that
is,
, that
is, 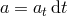 ;
;
- the functions
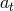 and
and 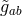 do not depend on the coordinates
do not depend on the coordinates 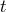 and
and 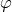 .
.
With respect to the resulting Papapetrou metric [144],
the field equations (54) become a set of partial differential equations on the two-dimensional Riemannian
manifold 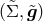 :
as is seen from the standard reduction of the Ricci tensor
:
as is seen from the standard reduction of the Ricci tensor 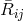 with respect to the static three-metric
with respect to the static three-metric
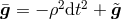 .
.
The last simplification of the field equations is due to the circumstance that 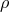 can be chosen as one of the
coordinates on
can be chosen as one of the
coordinates on 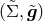 . This follows from the facts that
. This follows from the facts that 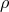 is harmonic (with respect to the Riemannian
two-metric
is harmonic (with respect to the Riemannian
two-metric 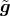 ) and non-negative, and that the domain of outer communications of a stationary black hole
spacetime is simply connected [44]. The function
) and non-negative, and that the domain of outer communications of a stationary black hole
spacetime is simply connected [44]. The function 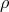 and the conjugate harmonic function
and the conjugate harmonic function  are called Weyl
coordinates.
With respect to these, the metric
are called Weyl
coordinates.
With respect to these, the metric 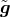 can be chosen to be conformally flat, such that one ends up with the
spacetime metric
can be chosen to be conformally flat, such that one ends up with the
spacetime metric
the 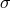 -model equations
and the remaining Einstein equations
for the function
-model equations
and the remaining Einstein equations
for the function 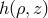 .
Since Eq. (58) is conformally invariant, the metric function
.
Since Eq. (58) is conformally invariant, the metric function 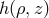 does not appear in the
does not appear in the 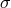 -model
equation (61). Therefore, the stationary and axisymmetric equations reduce to a boundary
value problem for the matrix
-model
equation (61). Therefore, the stationary and axisymmetric equations reduce to a boundary
value problem for the matrix 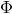 on a fixed, two-dimensional background. Once the solution
to Eq. (61) is known, the remaining metric function
on a fixed, two-dimensional background. Once the solution
to Eq. (61) is known, the remaining metric function 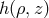 is obtained from Eqs. (62) by
quadrature.
is obtained from Eqs. (62) by
quadrature.
![]() , an asymptotically time-like Killing field
, an asymptotically time-like Killing field ![]() . Since
. Since ![]() and
and ![]() fulfill the
Frobenius integrability conditions, the spacetime metric can be written in the familiar
(2+2)-split.62
Hence, the circularity property implies that
fulfill the
Frobenius integrability conditions, the spacetime metric can be written in the familiar
(2+2)-split.62
Hence, the circularity property implies that ![]() can be chosen as one of the
coordinates on
can be chosen as one of the
coordinates on ![]() . This follows from the facts that
. This follows from the facts that ![]() is harmonic (with respect to the Riemannian
two-metric
is harmonic (with respect to the Riemannian
two-metric ![]() ) and non-negative, and that the domain of outer communications of a stationary black hole
spacetime is simply connected [44]. The function
) and non-negative, and that the domain of outer communications of a stationary black hole
spacetime is simply connected [44]. The function ![]() and the conjugate harmonic function
and the conjugate harmonic function ![]() are called Weyl
coordinates.64
With respect to these, the metric
are called Weyl
coordinates.64
With respect to these, the metric ![]() can be chosen to be conformally flat, such that one ends up with the
spacetime metric
can be chosen to be conformally flat, such that one ends up with the
spacetime metric